基于双曲正切函数的改进型永磁同步电机无感矢量控制系统

张攀， 石照耀， 林家春， 于渤， 孙衍强， 丁宏钰

(北京工业大学 精密测控技术与仪器工程技术研究中心，北京 100124)

永磁同步电机(permanent magnet synchronous motor, PMSM)具有结构简单紧凑、损耗低、功率密度高、调速性能好、动态响应快等优点，广泛应用于机器人、白色家电、数控机床、电动汽车、风机、泵机、激光追踪系统等领域[1-5]。随着永磁材料性能进步、电力电子元件性能的提升和PMSM控制技术的提高，PMSM应用领域也越来越广。PMSM常用的控制策略有磁场定向控制(field oriented control, FOC)又叫矢量控制和直接转矩控制(direct torque control, DTC)[6-7]。直接转矩控制相比矢量控制简化了控制结构和计算过程，缓解了运算控制器计算负担，但直接转矩较矢量控制产生更大的转矩脉动，在很多应用领域仍以矢量控制为首选方案。矢量控制方法通常使用光电编码器、磁编码器、旋转变压器来获取转子的准确角度信息参与控制计算。但是在很多应用场合，安装位置传感器不仅增加成本、整体尺寸、重量，也使得容易受外界振动、环境干扰，降低系统可靠性。无位置传感器控制方式可以降低PMSM对环境要求，简化系统结构。

PMSM无位置传感器控制方法大致分为零速、低速的高频信号注入法和中速、高速的反电势及磁链估计法[8-11]。国内外常用的无位置传感器感控制方法主要包括神经网络控制、模糊控制、扩展卡尔曼滤波器控制、龙伯格观测器控制、滑模变结构控制等[12-15]。其中，滑模控制对系统精度要求不高，对参数变化和外部干扰不敏感，是一种鲁棒性很强的控制方法，该方法在无位置传感器控制系统中应用最为广泛。在PMSM无位置传感器矢量控制中，基于给定电流与反馈电流间的误差构造滑模观测器。滑模观测器在观测转子位置和转速时，利用开关信号不断的变换系统结构，以很高的频率正负切换，快速修正反电动势的值，反电动势中包含着位置信息，利用反电动势解算出位置信息。由于滑模控制的固有特性，使用滑模观测器法会带来抖振问题，观测到的转子的位置信息容易受到转速的影响，所使用的开关函数对观测精度有较大影响[16]。

目前，改善滑模观测器的高频抖振是国内外学者研究的热点。文献[17]利用分段指数型函数代替传统滑模观测器中的开关函数，在饱和层内做线性变换，在饱和层外做开关函数变化，选取合适的边界层厚度，一定程度上减弱了高频抖动。文献[18]采用Sigmoid函数代替开关函数估计反电动势，减弱了转速的高频抖动。文献[19]对滑模观测器输出的反电动势进行两级滤波，提高了反电动的平滑度，增强了系统抗负载扰动能力。

本文提出了一种基于双曲正切函数代替开关函数的改进型滑模观测器，改善了传统滑模观测器的抖振问题。经滑模观测器输出的反电动势经过低通滤波之后仍存在较多的噪声信号，使用卡尔曼滤波器对低通滤波后的反电动势处理，再参与位置计算，提高观测精度。卡尔曼滤波器是一种非线性的随机观测器，不需要存储采集数据，可以实现边采集边计算，实现对采集数据的最优估计。同时使用锁相环来提取转子的位置信息、转速，进一步提高观测精度。通过构建李雅普诺夫(Lyapunov)方程对本文提出的改进型滑模观测器进行了稳定性判定，得到了进入滑模面的充分条件。最后在Simulink平台上对位置估算、转速估算、反电动势观测、电流观测、负载扰动及动态过程进行了仿真分析，通过对比分析验证了本文提出的滑模算法的可行性与精准性。

1 永磁同步电机数学模型

1.1 静止坐标系下PMSM数学模型

PMSM是一个强耦合、多变量、复杂的非线性系统，需要对其解耦分析，在α、β两相静止坐标系下数学模型为:

(1)

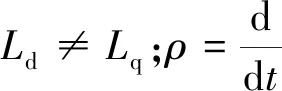
(2)

由式(2)可知扩展反电动势中包含位置信息，从扩展反电动势中可以提取转子电角速度ωe和电角度θe:

(3)

1.2 旋转坐标系下数学模型

在d-q旋转坐标下的数学模型为：

(4)

式中：ud、uq为d-q坐标系下的定子电压；id、iq为d-q坐标系下的定子电流；Ed、Eq为d-q坐标系下的感应电动势，且Ed=0，Eq=ωeψf，Eq包含着转速信息，通过对转速积分可得到转子的位置信息:

(5)

PMSM机械转矩方程式和电磁转矩方程为：

(6)

(7)

式中：J为转子转动惯量；Te为电磁转矩；TL为负载；B阻尼系数；pn电机极对数；ψf为定子磁链；ω为机械角速度。

2 改进型滑模观测器

2.1 旋转坐标系下滑模观测器构造

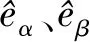
根据式(4)滑模观测器可构造为：

(8)

式(8)减去式(4)，得电流误差方程为：

(9)

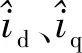
(10)

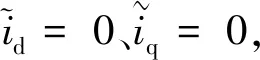
(11)

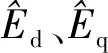
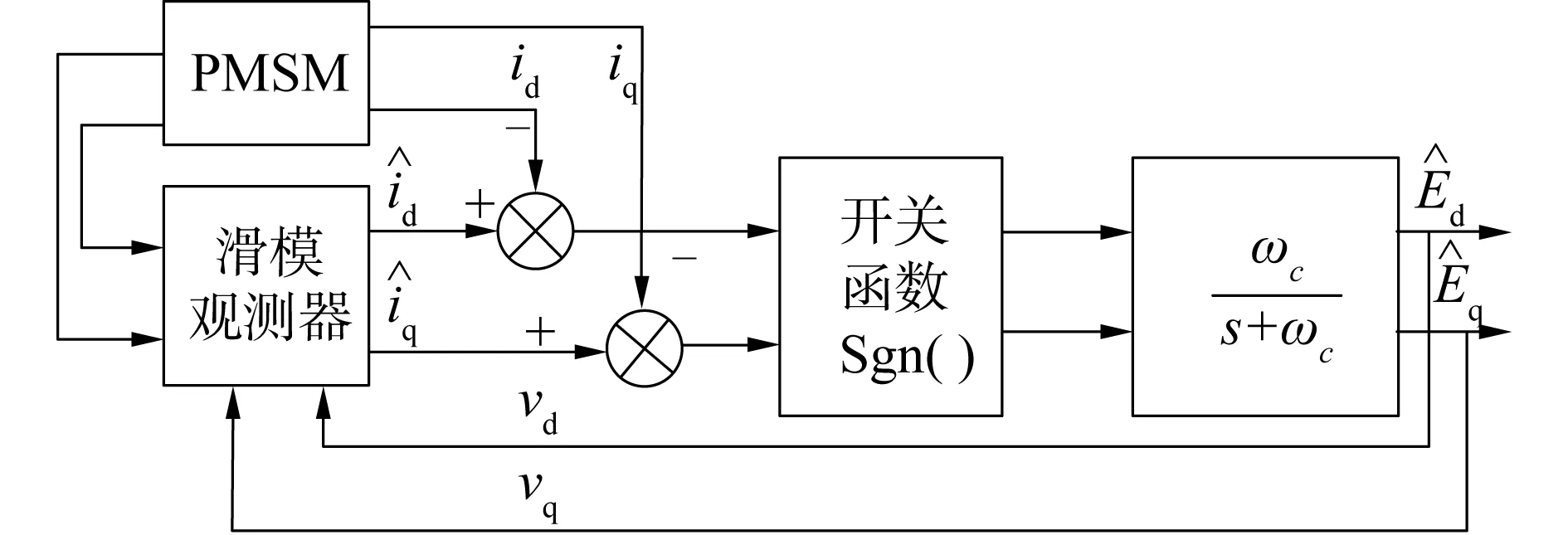
图1 传统滑模观测器结构Fig.1 Structure block diagram of traditional sliding mode observer

2.2 双曲正切函数滑模观测器构造

传统滑模观测器中使用的是不连续的开关函数，某些改进型的控制策略将开关函数改为饱和函数，在一定程度上改善了开关函数突变造成的抖振问题，但是仍有较大抖振。为最大程度减弱开关函数带来的抖振问题，本文采用双曲正切函数代替开关函数。开关函数、饱和函数、双曲正切函数曲线如图2所示。

图2 开关函数、饱和函数、双曲正切函数曲线Fig.2 Curves of sgn(·) function, sat(·) function, tanh(·) function

根据实际控制要求将双曲正切函数修改为：

(12)

式中：α为权重因子，α越小边界层厚度越大，系统收敛越慢，且系统的鲁棒性越差，当α无穷大时，f(x)转换为开关函数，造成较大的抖振，本文选取α值为2.2，满足系统的精度和鲁棒性要求。使用双曲正切函数代替滑模函数则，式(8)改写为：

(13)

双曲正切函数变化平缓，不存在突变，一定程度上削弱了滑动模态运行过程中的高频抖动。

2.3 李雅普诺夫稳定性分析

不同改进型的滑模观测器，最终都要使估计值收敛到滑模面。当电流误差为负值时，电流误差的微分值要为正，修正电流减小的趋势；当电流误差为正时，电流误差的微分值要为负，修正电流增加的趋势。使用李雅普诺夫(Lyapunov)函数判断双曲正切函数滑模观测器的稳定性。Lyapunov稳定性方程为：

V=sTs/2

(14)

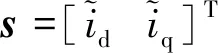
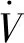
(15)

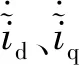
(16)

对于表贴式PMSM有Ld=Lq=Ls，对于内嵌式PMSM为化简方便，可认为Ld=Lq=Ls=(Ld+Lq)/2，将式(16)代入式(15)得：

欧洲脑白质疏松和残疾研究（LADIS）是一项纳入396名受试者的大样本的前瞻性的随机对照研究，研究发现受试者的糖尿病病史、空腹血糖水平，以及既往脑卒中病史与脑白质损害的进展有着显著的相关［15］。

(17)

(18)

2.4 感应电动势卡尔曼滤波

低通滤波器设置的截止频率过大，则感应电动势中含有的干扰信号较多，滤波效果不明显；若截止频率选得过小，会导致估算感应电动势中存在较大的相位误差。低通滤波处理后感应电动势中仍然存在着估算误差和谐波分量，可进行二级滤波处理，减小谐波分量，卡尔曼滤波器不仅可以滤除感应电动势中的高频分量，还能够对系统噪声和测量噪声进行过滤处理，提高观测精度[20]。卡尔曼滤波是一个不断预测、修正的过程，能够实现实时采集预测，不需要存储历史测量数据，非常适合在MCU运算处理器中实时滤波处理。

由于系统采样周期极短可以认为k时刻和k-1时刻感应电动的值没有变化，则无控制量的离散卡尔曼滤波状态预测方程为：

(19)

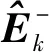
(20)

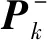
(21)

式中：Kk表示k时刻的卡尔曼增益；H为测量模型的参数矩阵，一维时可设置为1；R为噪声的协方差。

根据k时刻的感应电动势估计值和k时刻低通滤波输出的值，可以得到k时刻感应电动势最优估计值，也就是k时刻滤波后的值。

(22)

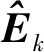
(23)

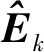
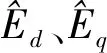
2.5 锁相环估算转子位置

电机实际运行过程中磁链ψf并不是一个常量，受负载、温度变化的影响，经除法运算求得转速不准确，造成角度估算存在较大误差。为改善这种除法运算引入的误差，采用锁相环(phase-locked loop，PLL)的方式来获取转子的位置观测值。将三相电压变换到d-q坐标系有：

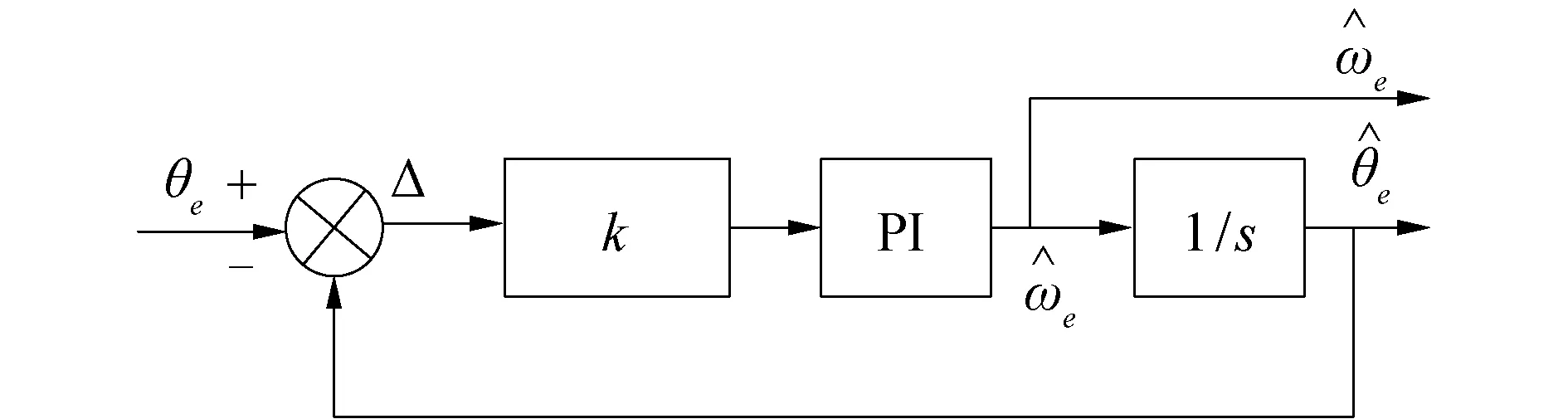
图3 锁相环转子位置估算Fig.3 Estimation of PLL rotor position

根据图3计算等效锁相环的系统传递函数为：

(24)

式中：k为增益系数；kp、ki为PI环的比例、积分系数。

从式(24)可以看出G(s)具有低通滤波的作用，可以减弱估算电角度中的高频谐波，与式(5)相比，虽然锁相环系统动态性能弱一些，但锁相环法提取的角度信息和转速信息误差更小，具有更高的观测精度和更强的鲁棒性。基于双曲正切函数的改进型滑模观测器结构如图4所示。

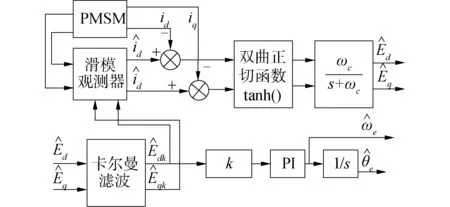
图4 双曲正切函数的改进型滑模观测器Fig.4 Improved sliding mode observer based on tanh(·) function

3 仿真实验结果与分析

3.1 速度变化结果分析

为验证改进型滑模观测器的可行性，本文基于Simulink仿真平台进行仿真验证。系统仿真时间为1.8 s，采用id=0控制策略，永磁同步电机的关键参数设置如表1所示。

设置目标转速为800 r/min，在0.5 s时突然施加1 N·m负载，0.8 s时卸载，1.1 s时施加3 N·m负载，1.4 s时卸载，反复加载卸载，根据仿真结果，观测系统仿真特性。滑模观测系统均使用锁相环控制估算转子的位置信息。3种控制策略的电流环、速度环、锁相环中的PI控制参数完全相同。基于开关函数、饱和函数、双曲正切函数滑模观测器控制系统仿真结果的速度变化曲线如图5～7所示。

表1 永磁同步电机参数Table 1 Parameters of PMSM

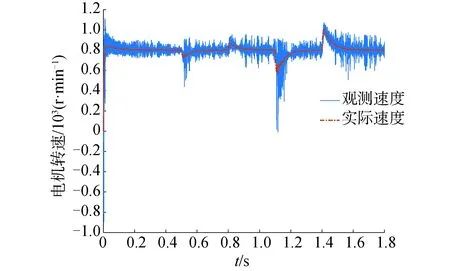
图5 基于开关函数的滑模观测器速度变化曲线Fig.5 Speed curves of sliding mode observer based on sgn(·) function

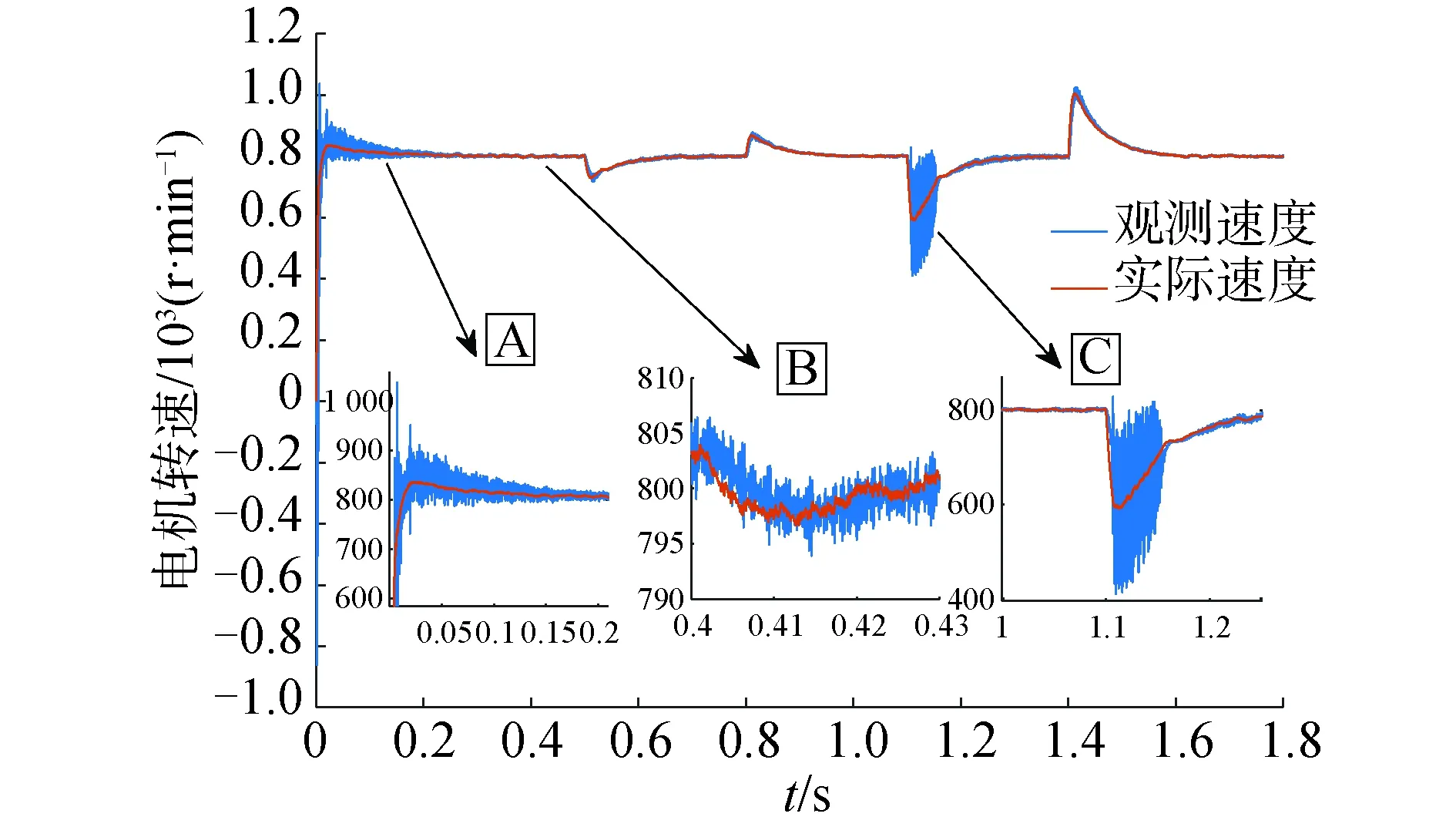
图6 基于饱和函数的滑模观测器速度变化曲线Fig.6 Speed curves of sliding mode observer based on sat(·) function

图7 基于双曲正切函数的滑模观测器速度变化曲线Fig.7 Speed curves of sliding mode observer based on tanh(·) function

由图5～图7中可以看出，稳态时饱和函数和双曲正切函数的速度平稳性要明显优于开关函数。在受到外界负载冲击时饱和函数和双曲正切函数的抗干扰能力明显优于开关函数。在0.5 s突然施加1 N·m负载，在0.8 s时卸载，饱和函数和双曲正切函数的速度曲线变化没有明显区别。对比图6、图7中的A部分放大图，在启动瞬间饱和函数观测速度振荡幅度超过了1 000 r/min，明显大于双曲正切函数观测速度振荡幅度950 r/min。之后的启动过程中，二者都存在明显的振荡。但双曲正切函数仍存在明显的大幅振荡幅值和较长的收敛时间，在启动阶段的稳定性并没有得到较大改善。对比图6、图7中的B部分放大图，稳态时双曲正切函数的速度波动在5 r/min内，小于饱和函数的速度波动，削弱了无感稳态速度抖动。

在1.1 s突然施加3 N·m负载，在1.4 s时卸载该负载，可以看到在突然施加负载时双曲正切函数的抗干扰能力要明显优于饱和函数。对比图6、图7中的C部分放大图，饱和函数的最低速度接近400 r/min，而双曲正切函数的最低速度接近500 r/min，并且饱和函数的速度变化存在较大的振荡，速变化不平稳，而双曲正切函数的速度变化曲线比较平滑，在PI的调节作用下逐渐达到目标速度。受到较大冲击时，双曲正切函数较饱和函数具有更强的抗干扰能力。在1.4 s时卸载二者的速度变化基本相同。

3.2 电动势变化结果分析

图8～图10显示的是反电动势eα、eβ变化曲线。由图8～图10中可以看出基于饱和函数的反电动势和基于双曲正切函数的反电动势明显优于基于开关函数的反电动势。转速变化直接反应了反电动势的变化，开关函数的速度变化较剧烈，其反电动势变化也不稳定。

图8 基于开关函数的滑模观测器反电动势变化曲线Fig.8 Back EMF curve of sliding mode observer based on sgn(·) function

启动瞬间基于饱和函数的振荡幅值要明显大于基于双曲正切函数幅值。在0.5 s突然施加1 N·m负载，在0.8 s时卸载，二者的反电动势都没有明显的区别，但是在0.8 s时突然施加3 N·m负载基于饱和函数的反电动势曲线出现了明显紊乱，振荡的幅值和收敛时间都要大于双曲正切函数。基于双曲正切函数的反电动势出现短时振荡后便逐渐收敛，在1.4 s时卸载，二者的反电动势出现了轻微的波动，但区别不是很明显。由式(2)表明了反电动势与转速之间的关系，根据转速仿真结果、反电动仿真结果以及上述的分析，可知仿真结果的合理性。

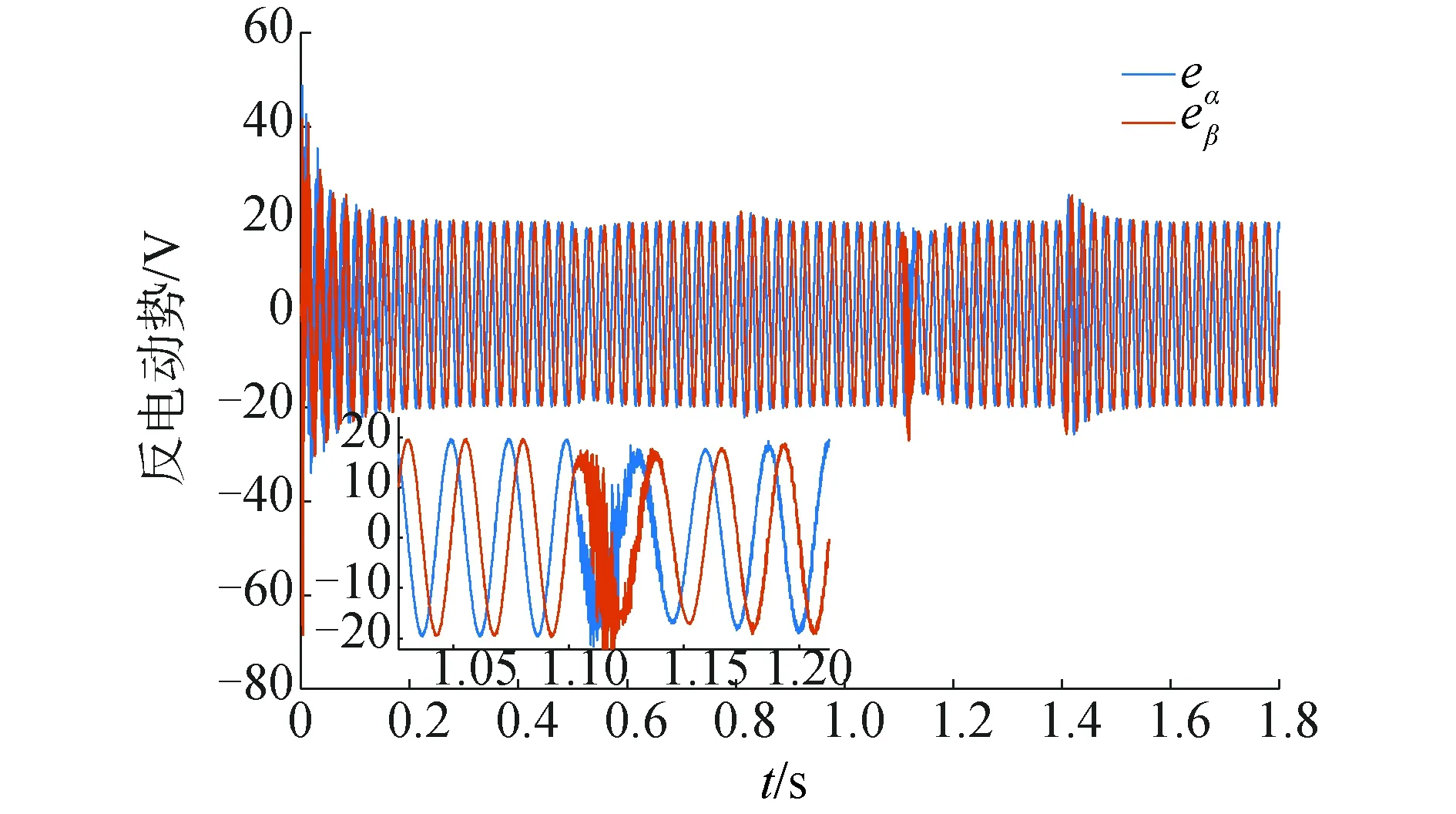
图9 基于饱和函数的滑模观测器反电动势变化曲线Fig.9 Back EMF curve of sliding mode observer based on sat(·) function

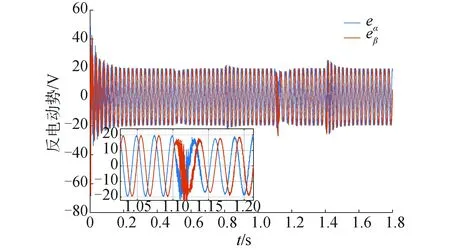
图10 基于双曲正切函数的反电动势变化曲线Fig.10 Back EMF curve based on tanh(·) function

3.3 电流变化结果分析

图11～图13显示是三相电流变化曲线。

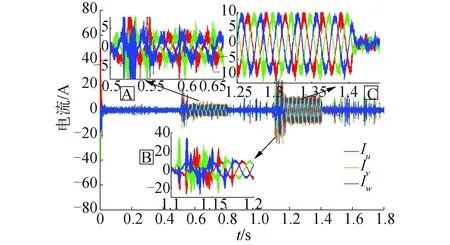
图11 基于开关函数的电流曲线Fig.11 Current curve based on sgn(·) function

由图11～图13可知，开关函数的电流变化曲线含有较多的高频谐波，电流波动较大。在施加负载时开关函数电流振荡幅度较大，电流畸变明显，收敛速度慢。对比图12和图13中的局部放大图A，在0.5 s时施加1 N·m负载，基于饱和函数和基于双曲正切函数的三相电流变化曲线差别不是很明显。在1.1 s时突加3 N·m负载，对比局部放大图B，双曲正切函数电流相比饱和函数电流畸变小，且能在更短的时间内迅速调节到规律的正弦变化曲线，证明基于双曲正切函数的抗干扰能力较强。对比局部放大图C，施加负载进入稳定阶段后二者的电流变化曲线没有明显区别。

图12 基于饱和函数的电流曲线Fig.12 Current curve based on sat(·) function

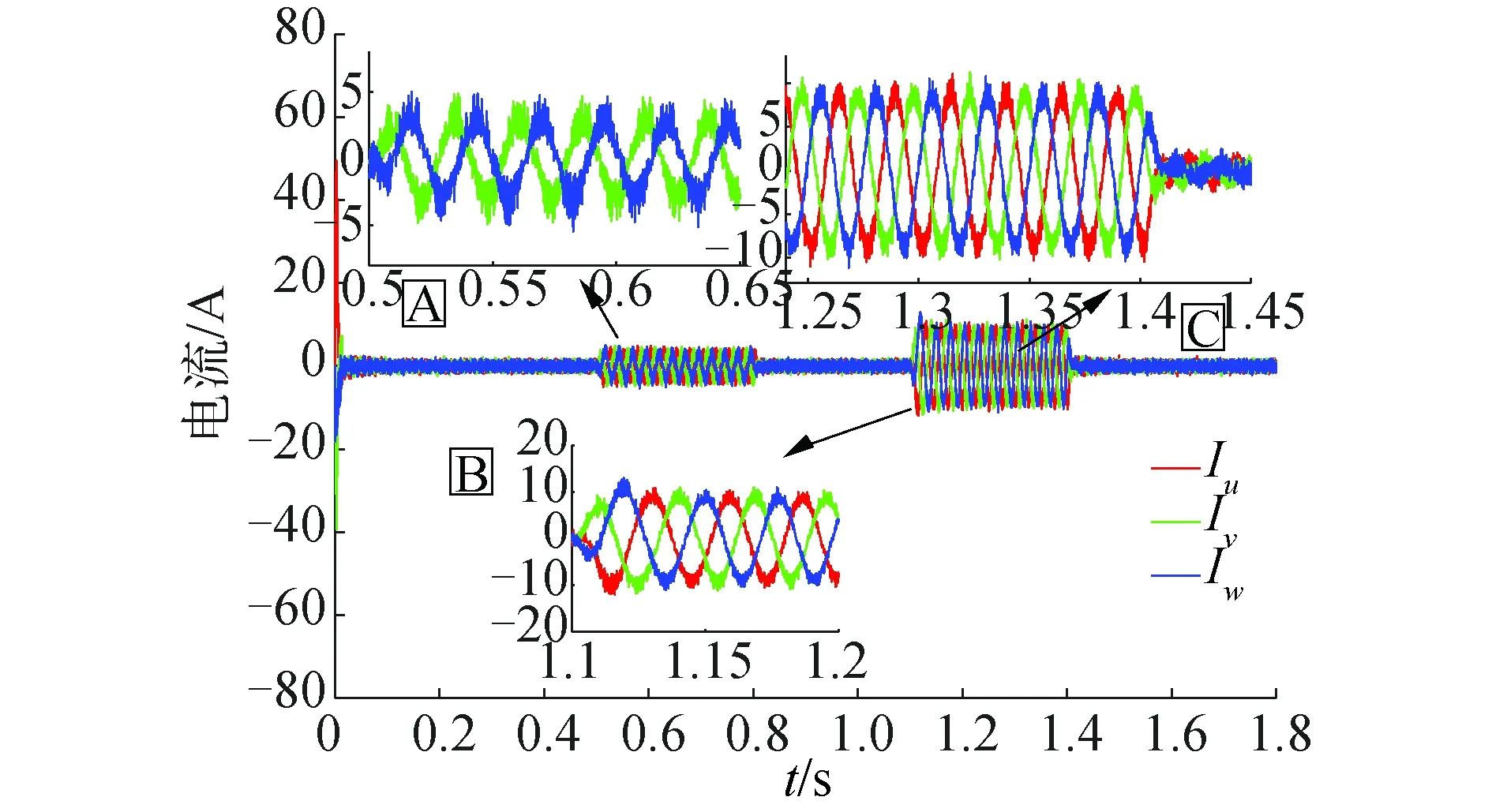
图13 基于双曲正切函数的电流曲线Fig.13 Current curve based on tanh(·) function

3.4 转速误差变化曲线分析

图14～图15显示的是饱和函数和双曲正切函数转速误差变化曲线。由图5可以看出基于开关函数的观测速度在空载和负载情况下跟实际速度有较大的误差，不做详细对比。

图14 基于饱和函数的转速误差曲线Fig.14 Speed error curve based on sat function

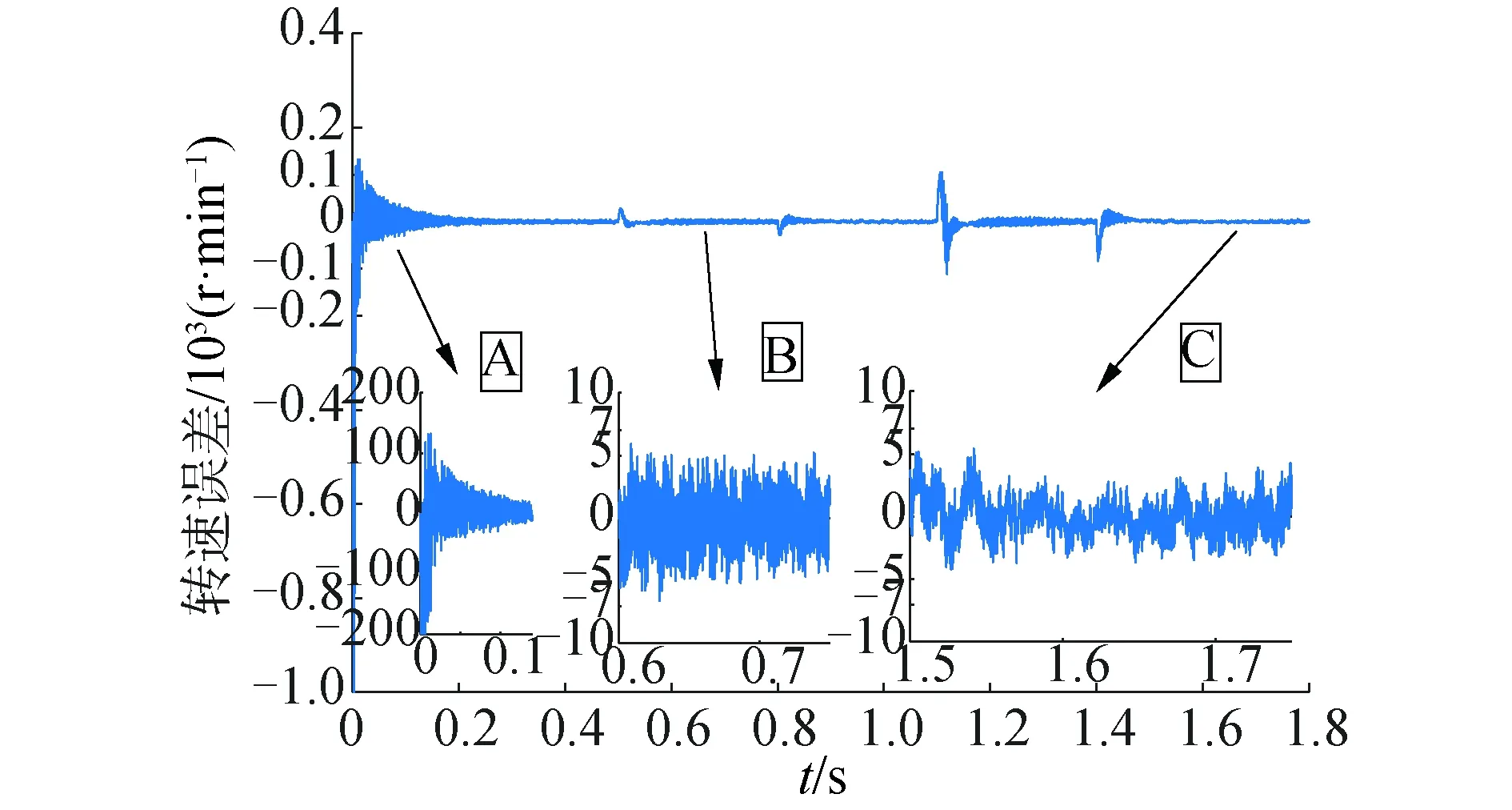
图15 基于双曲正切函数的转速误差曲线Fig.15 Speed error curve based on hyperbolic tangent function

由图14～图15启动阶段的A部分局部放大图可知，双曲正切函数的振荡的最大幅值小于饱和函数的最大幅值，但仍存在较大的振荡。两处稳态运行阶段的局部放大图B、C，基于双曲正切函数的估算转速与实际转速在-7～6 r/min范围内变化，基于饱和函数的估算转速与实际转速在-8～8 r/min范围内变化，稳态运行时双曲正切函数较饱和函数对抖振现象有所缓解。在0.5 s施加1 N·m负载，在0.8 s卸载，二者的转速误差曲线差别不太明显，但在1.1 s时施加3 N·m负载，在1.4 s卸载，双曲正切函数的振幅明显小于饱和函数的振幅，并且在较短的时间内收敛到目标值附近，具有较强的抗干扰能力。

3.5 带卡尔曼滤波的速度变化分析

通过上述仿真可以证明双曲正切函数具有较强的削弱稳态抖振能力和较强的抗干扰能力。为进一步改善双曲正切函数启动过程振荡幅度大和稳态运行的抖振问题，在反电动势末端加入卡尔曼滤波，由于电流变化和反电动势变化都能在速度曲线上体现出来，这里只分析速度和速度误差变化曲线，图16～图17是在双曲正切函数基础上加入卡尔曼滤波的速度变化曲线和速度误差变化曲线。

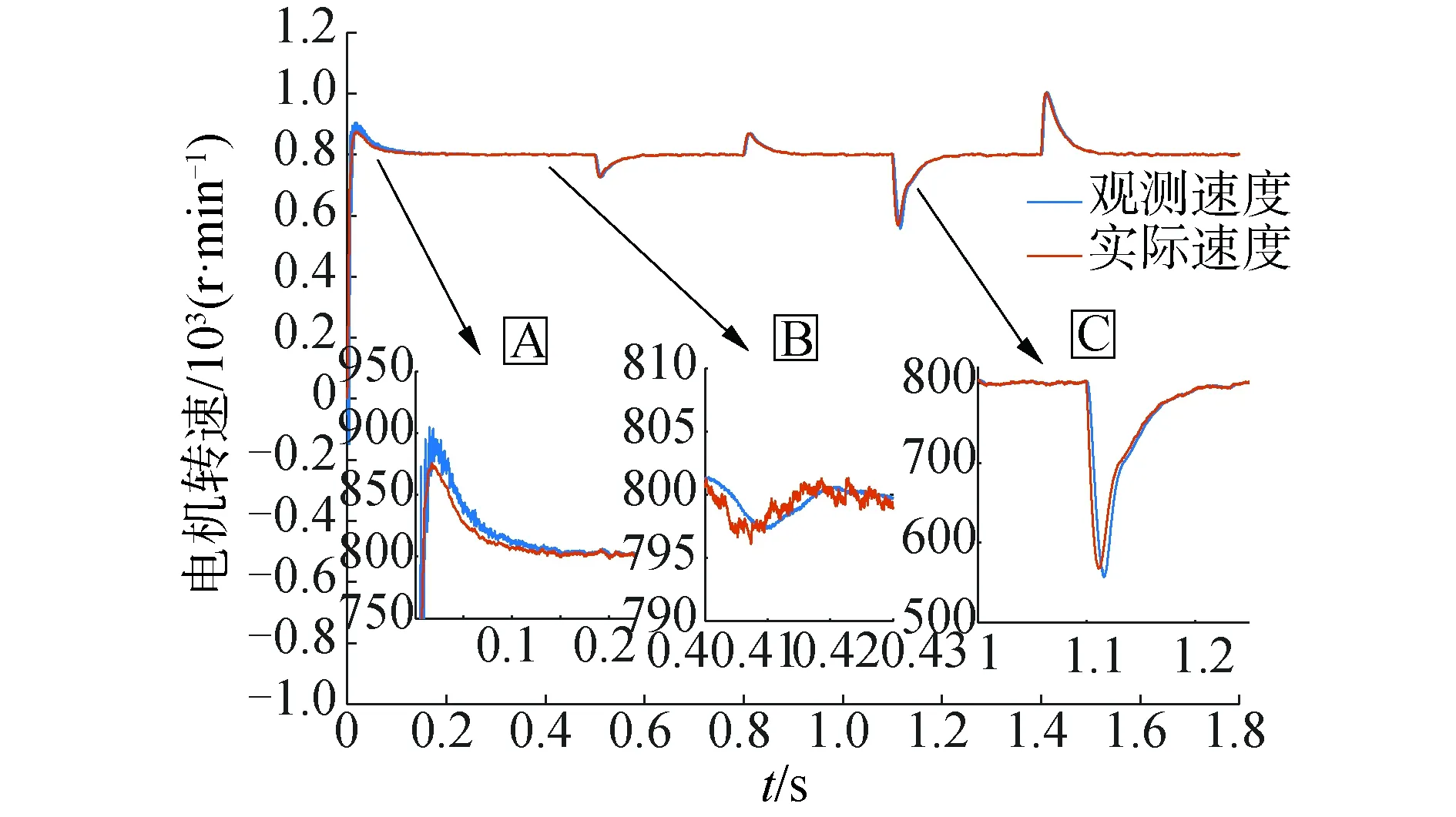
图16 带卡尔曼滤波器的速度变化曲线Fig.16 Speed curve of Kalman filter

对比速度变化曲线图7和图16的局部放大图A，经过卡尔曼滤波后启动过程的振荡频率与振荡幅值得到明显改善，从之前的950 r/min降低到900 r/min，收敛时间也明显减小从之前的0.2 s缩短至0.1 s。对比局部放大图B 可知在稳态运行时，加入滤波后的稳态运行误差值更小。局部放大图C是施加3 N·m负载的速度波动曲线，估算速度的振荡频率与最大振荡幅值明显减小，图16经卡尔曼滤波后的最小速度约为580 r/min，明显大于图7无卡尔曼滤波的最小速度500 r/min。图16中在1.2 s时达到目标速度，图7中在1.25 s时达到目标速度，收敛时间减小。

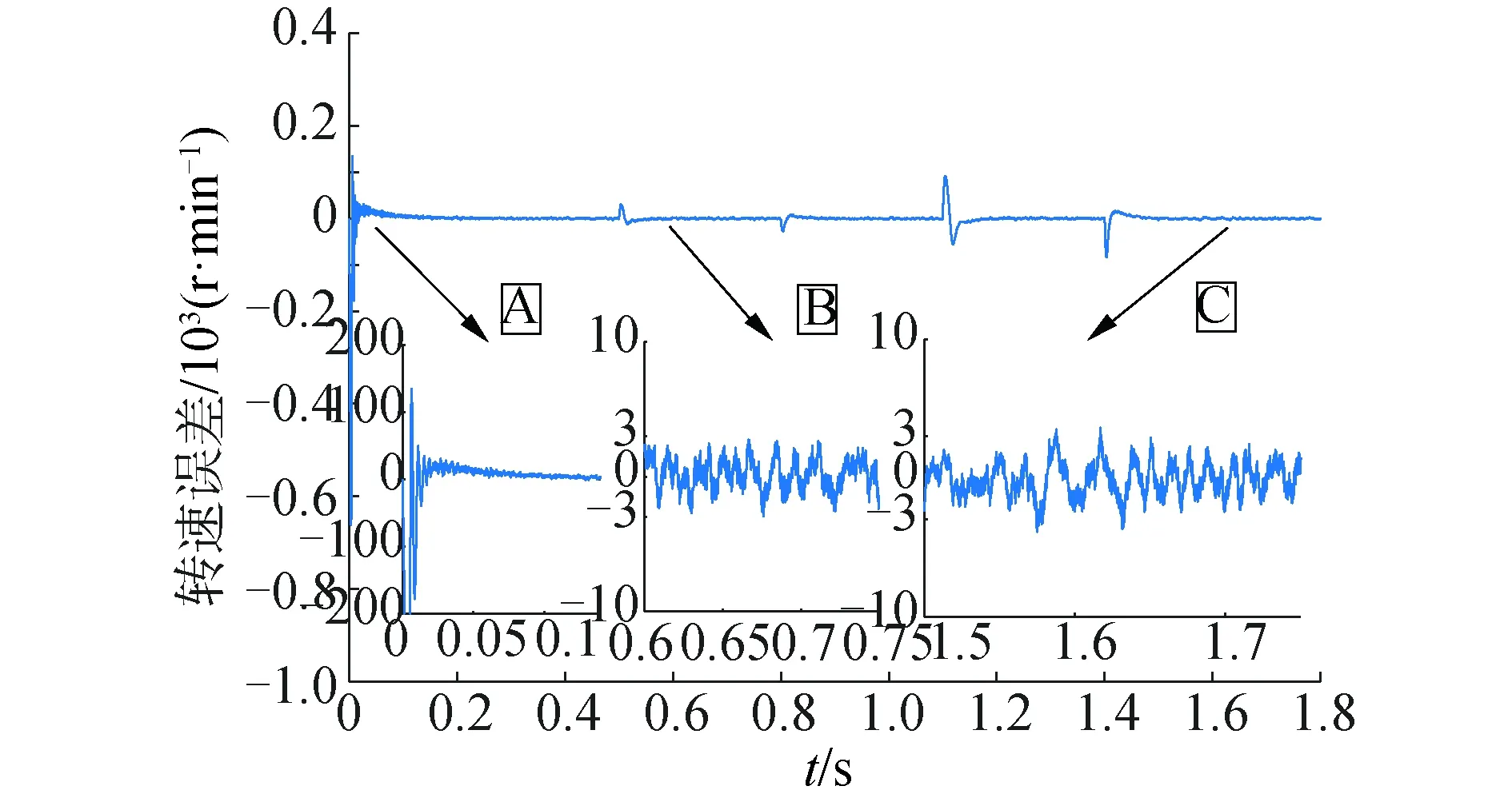
图17 带卡尔曼滤波器的速度误差变化曲线Fig.17 Speed error curve of Kalman filter

加入卡尔曼滤波器后系统抗干扰能力明显增强。对比图15和图17，加入卡尔曼滤波后启动过程速度误差波动曲线在0.05 s时基本达到稳定，启动过程的振荡得到明显改善，从B部分和C部分是稳态运行过程的局部放大图，振荡幅值得到明显改善，由之前的-7～7 r/min缩小到-3～3 r/min。

通过对图7和16，图15和17的对比分析可以证明加入卡尔曼滤波后明显改善了启动阶段的振荡幅值与收敛时间，并且进一步削弱了稳态运行过程中的高频抖振问题。

4 结论

1)采用改进型滑模控制算法在稳定运行过中的速度误差明显减小，缩小到-3～3 r/min，改善了稳态的抖振问题。

2)当外界突加负载时，改进型滑模控制方法适应能力最佳，具有最强的抗干扰能力，能够更好的保持三相电流稳定。

3)对反电动势进行卡尔曼滤波后，启动过程的速度振荡幅度与收敛时间明显减小，启动过程更为平滑。