冰下脉冲噪声特性及信号检测性能分析
廖志宇, 朱广平, 殷敬伟, 王成, 赵宿辰, 秦振林
(1.哈尔滨工程大学 水声重点实验室, 黑龙江 哈尔滨 150001; 2.海洋信息获取与安全工业和信息化部重点实验室 (哈尔滨工程大学), 黑龙江 哈尔滨 150001; 3.哈尔滨工程大学 水声工程学院, 黑龙江 哈尔滨 150001)
近年来由于地球变暖的趋势,北极冰区面积持续减少,北极航道有望开通。又由于北极高纬度地区丰富的自然资源,引起了各海洋大国的高度关注。水声技术是开发极地的有力手段,北极水声学已成为新的研究热点。北极地区地理位置独特、气候寒冷,北冰洋的大部分区域终年被海冰覆盖,具有特殊的海洋环境,很多新问题和新现象渐渐地被从事该领域研究工作者所注意,研究发现了很多新的研究成果[1-4]。由于冰盖的作用,北极也形成了独特的声场环境,造成冰下噪声剧烈起伏以及强混响效应, 并形成了北冰洋独有的半波导声道。近些年来我国很多科研工作者在北极开展科学研究,刘洪宁等[5]研究发现加拿大海盆海冰边缘区是声体积后向散射强度的明显过渡区;刘崇磊等[6]开展了基于声场模型的扩频通信技术在北极冰下声信息传输中获得了良好的通信性能的成果;黄海宁等[7]分析北极冰下声信道多途结构,提出了基于OASES-Bellhop耦合模型的冰下声信道多途结构快速分析方法;朱广平等[8]将Burke-Twersky(BT)散射模型与射线理论相结合研究了北极典型冰下的水声信道特性,对认知极地冰下水声信道特性以及开展极地水声系统性能预报具有一定意义。随着水声技术的不断发展,冰下噪声对声呐检测性能的影响也受到了越来越广泛的关注[9]。在传统的声呐信号检测性能分析中,常用高斯分布对其进行建模和理论研究。然而,冰下噪声信号脉冲值出现较频繁,具有很强的脉冲特性,统计上表现出较厚的拖尾,具有很强的非高斯性[10]并且常包含很多的瞬变信号[11-12]特性。采用高斯模型对冰下噪声进行建模研究分析会导致检测性能不准确,在严重时甚至会失效[13]。因此有必要对冰下脉冲噪声特性及其对检测性能的影响进行深入分析。
Alpha稳定分布由Levy于1925年在研究广义中心极限定理时提出,它是满足广义中心极限定理的唯一分布。田亚男等[14]分析了北极脉冲噪声的特性并对其进行了声信道估计,描述了北极冰噪声具有厚重拖尾的特性。宋国丽等[15]表明了Alpha稳定分布对尖峰态噪声建模的可行性和适应性。刘晔等[16]分析了浅海环境下混响形成过程及其非高斯特性,采用对称 Alpha 稳定分布理论对其进行了建模,验证了模型的有效性。所以,采用Alpha稳定分布对有关冰下噪声方面的建模具有可行性。
本文分析了第8次北极科考声学实验采集的冰下噪声及松花江冰下噪声统计特性,采用Alpha稳定分布对噪声进行建模,采用蒙特卡罗方法在实际噪声及仿真噪声下分析匹配滤波器的检测性能,重点分析了不同参数的Alpha稳定分布噪声、不同的发射信号及信噪比对检测性能的影响。
1 Alpha稳定分布
1.1 Alpha稳定分布表达式
Alpha稳定分布除了几个特例外,没有统一、封闭的解析表达式,通常使用特征函数来描述其分布特性,其特征函数表达式形式为[17-18]:
φ(x)=exp{iδx-|γx|α[1+iβsgn(x)ω(x,α)]}
(1)
式中:
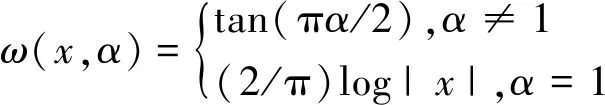
(2)
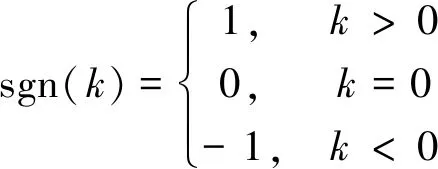
(3)
式中:α、β、γ、δ确定了Alpha稳定分布的特征函数。
1.2 Alpha稳定分布参数性质
假设变量X服从Alpha稳定分布,则有X~Sα(γ,β,δ),各个参数的性质如下:
1)α是Alpha稳定分布的特征指数,决定了噪声脉冲特性的强弱即概率密度函数的拖尾厚度。其数值范围是0<α≤2,α趋近于0的时候,噪声的脉冲特性越来越明显,概率密度函数的拖尾程度加重。当α=2时,Alpha稳定分布退化为高斯分布即S2(γ,0,δ)=N(δ,2γ2);当α=1时,Alpha稳定分布退化为柯西分布S1(γ,0,δ);当α=0.5,β=1的时候Alpha稳定分布退化为Levy分布S0.5(γ,1,δ)。
2)β是Alpha稳定分布的偏斜参数,表示分布的倾斜程度。其数值范围是:-1≤β≤1,当β<0时,Alpha稳定分布的概率密度函数的峰向右倾斜,分布向左倾斜;当β>0时,概率密度函数的峰向左倾斜,分布向右倾斜。当β=0时,概率密度函数为对称的,此时分布称为对称Alpha稳定分布。
3)γ是Alpha稳定分布的尺度参数,描述了Alpha稳定分布的离散程度,其数值范围是0≤γ<∞,类似于高斯分布的方差。
4)δ是Alpha稳定分布的位置参数,决定了概率密度函数峰值所处位置,其范围是-∞<δ<+∞。当β=0,γ=1,δ=0,Alpha稳定分布对应标准SαS分布。
1.3 Alpha稳定分布噪声仿真方法
可以通过S1参数系、S2参数系、标准参数系生成服从Alpha稳定分布的随机变量。S1参数系消除了标准参数系特征函数存在的不连续性[19],S2参数系下随机变量产生的方法便于理论证明[20],采用S2参数系以及Alpha稳定分布的基本性质生成服从Alpha稳定分布的随机变量。
产生2个互相独立的随机变量V和W,其中V是服从(-π/2,π/2)的均匀分布,W是服从均值为1的指数分布。
当α≠1时,
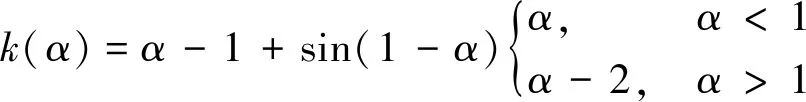
(4)
(5)
(6)
当α=1时,β2=β:
(7)
(8)
通过式(8)得到X即是服从Alpha稳定分布的随机变量。
1.4 分数阶矩法估计分布参数
满足位置参数δ=0的实对称Alpha稳定分布随机变量具有有限的分数低阶矩,本文采用分数低阶矩法对Alpha稳定分布的α、γ进行参数估计[21],测试过程中发现α、γ过大时发生对参数γ的估计严重不准确,故对公式加以稍加改动,在不影响对α估计性能的前提下改善了对参数γ的估计性能,具体过程如下:
令随机变量的正负阶数为p、q,则正负阶矩分别为:
(9)
(10)
(11)
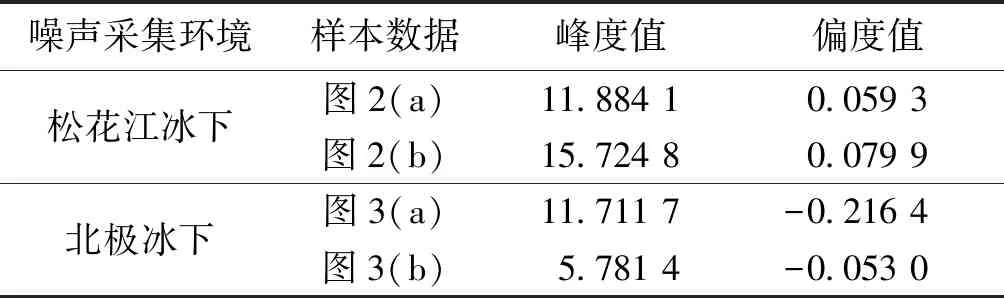
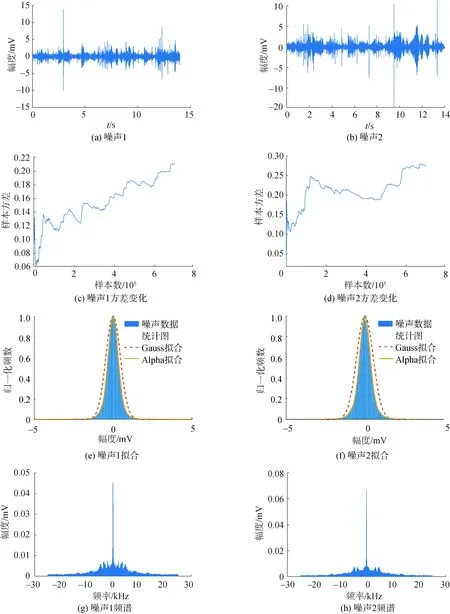
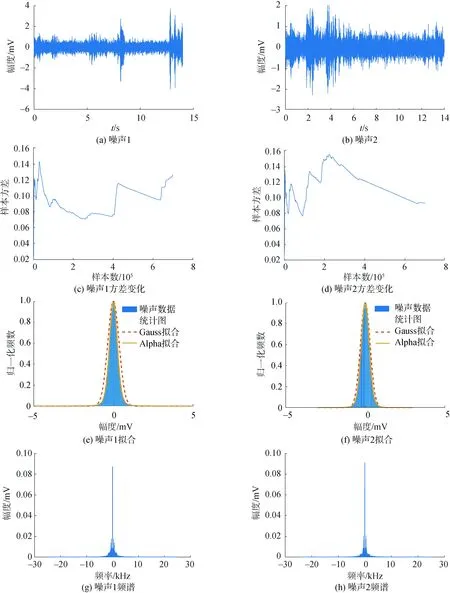
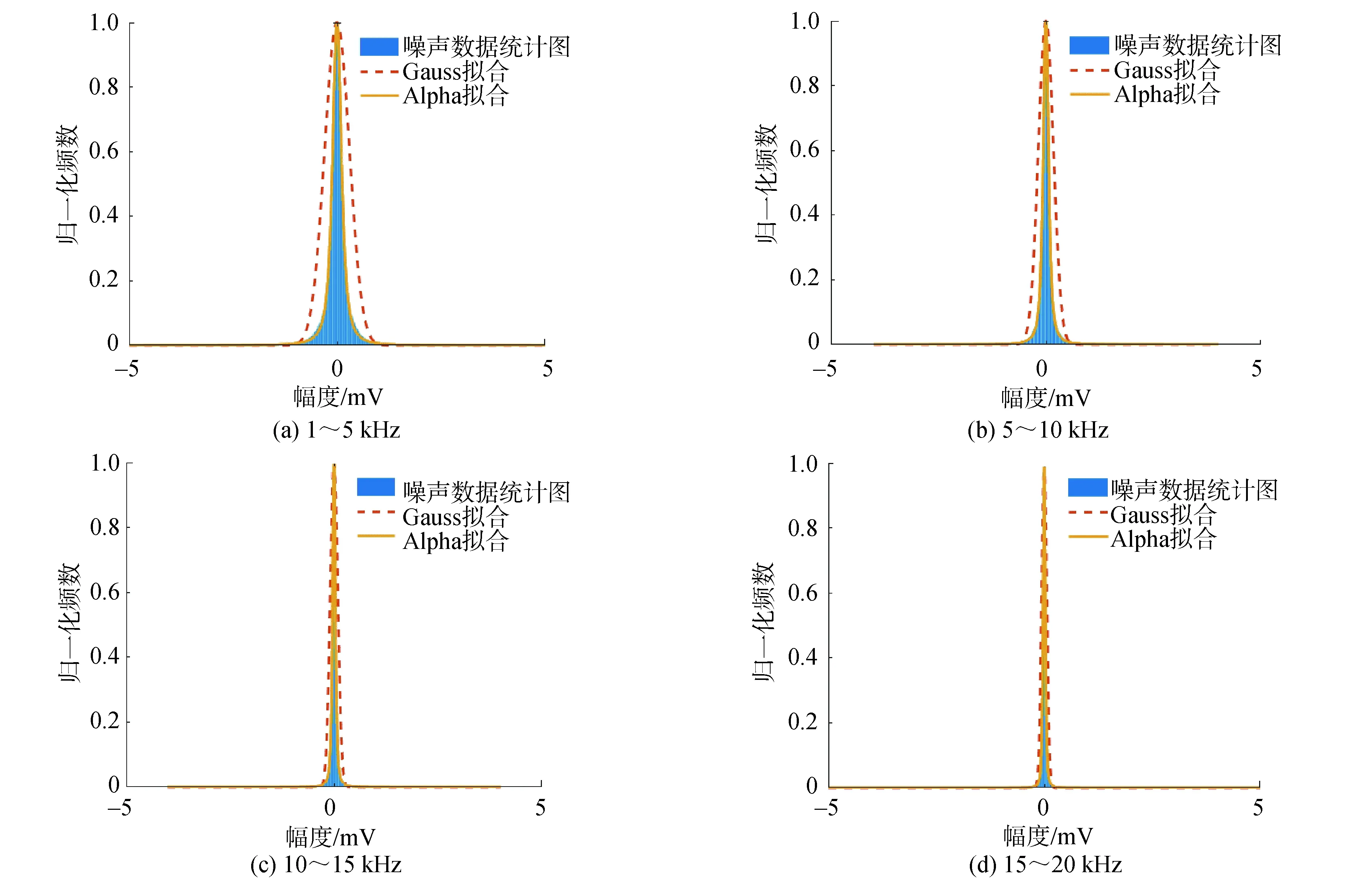
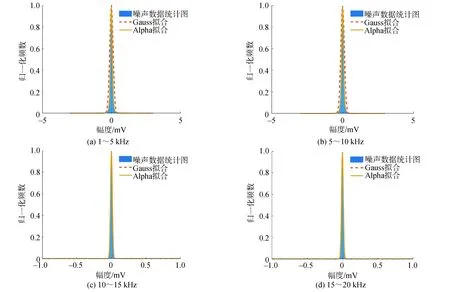
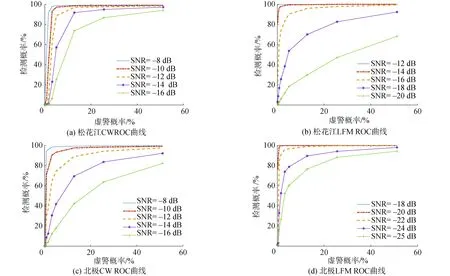
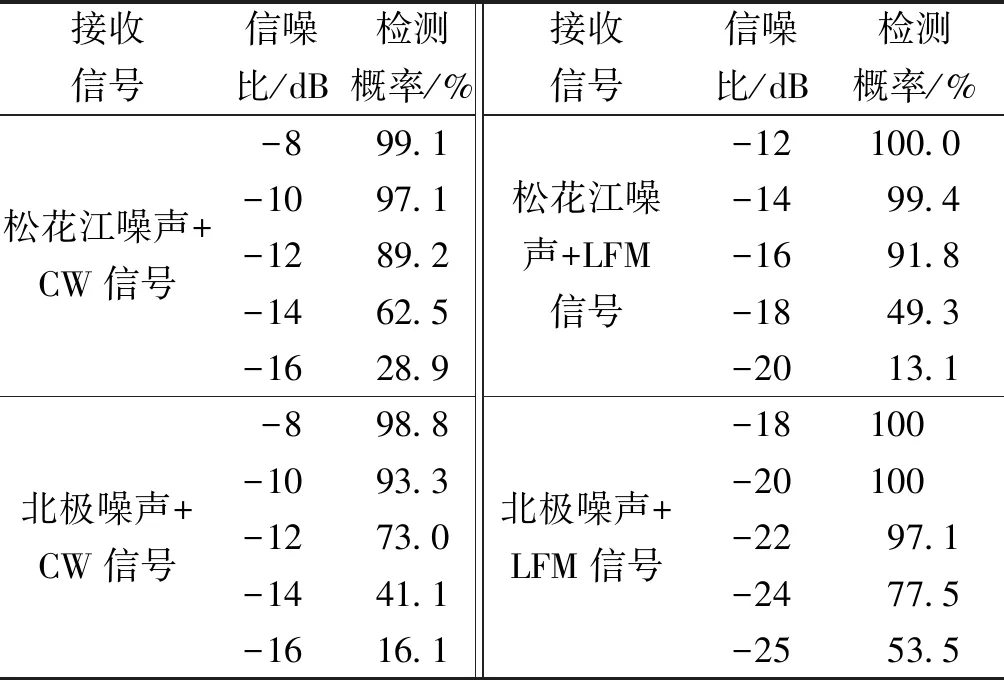
令p=-q,以保证正负阶矩均有限,则有0 0 (12) 进而根据式(13) 估计出参数γ的值: (13) p值越小,对于α、γ的估计越准确[22]。在估计的过程中,样本点数为5 000,p=0.1,当估计α的数值时令γ=1,估计γ的数值时令α=1对α、γ的估计情况如表1。 表1 参数α、γ估计情况统计表Table 1 Parameter α,γ estimation statistics table 分析冰下噪声的高阶统计量如偏度值和峰度值,也有利于充分认知其非高斯特性,峰度和偏度均无量纲。偏度(Skewness)反映了随机变量分布对称情况,定义为样本的三阶矩,其计算公式为: (14) 峰度(Kurtosis) 反映了随机变量分布的尖锐程度,峰度越大,表现在分布上面是中心点越尖锐。在相同方差的情况下,峰度越大,中间一大部分的值方差都很小,必须有一些值离中心点越远,所以这就是所说的“厚尾”,定义为四阶标准矩,其计算公式为: (15) 式中:μ是均值;δ为标准差;E是均值操作。 当输入为确定信号加上平稳噪声时,能够使输出信噪比达到最大值的线性系统称为匹配滤波器。 (16) 式中:s0(T)为输出信号;n0(T)为输出噪声;h0(t)为冲激响应。使SNR最大等效于在输出信号功率E[s02(T)]为常数的约束条件下,使输出噪声功率E[n02(T)]最小。这是一个有约束条件的最优化问题,应用拉格朗日(Lagrange)乘数法构建目标函数对其求导,当施瓦兹不等式中等号成立时: (17) 式(17)就是匹配滤波器传输函数的普遍形式。匹配滤波器的作用主要有2个方面:1)使滤波器输出有用信号成分尽可能强;2)抑制噪声,使滤波器输出噪声成分尽可能小,减小噪声对信号处理的影响。在声呐雷达信号处理中这2个作用都是以输出信噪比最大为准则来提高信噪比。 首先将噪声样本(北极噪声样本或仿真噪声样本)与拷贝信号(发射信号)进行叠加形成目标回波样本集(以下统称样本集),然后将拷贝信号分别与噪声样本以及目标回波样本集做匹配滤波进行信号检测。采用蒙特卡罗方法做1 000次重复匹配滤波实验。根据信号样本和噪声样本的检测结果,设置一定的检测阈值。在这一过程中,每次计算出2个重要量的值,ROC曲线的纵轴是“检测概率”(true positive rate, TPR),横轴是“虚警概率”(false positive rate,FPR)分别以它们为横、纵坐标作图,就得到了“ROC曲线”,该曲线描述了在不同虚警情况下对信号的检测情况。检测性能分析流程如图1所示。 图1 检测性能分析流程Fig.1 Flow chart of test performance analysis 研究过程中所采用的数据为松花江实验采集的冰下噪声数据和北极冰下噪声数据,松花江噪声数据为2020年1月份在松花江冰面破洞,由水听器采集获得,温度为-18 ℃左右,冰层厚度在46 cm左右,北极噪声数据为第8次北极科考采集的数据。对噪声数据进行脉冲特性分析,展示部分冰下噪声样本图,绘制了其相应的统计分布直方图并采用Alpha稳定分布和高斯分布对噪声数据进行了拟合并对比了二者拟合效果,噪声数据的采样频率fs=50 kHz。 图2描述了松花江冰下噪声数据及拟合情况。图2(a)、(b)是在松花江冰下噪声数据时域图,图2(c)、(d) 描述了样本方差随松花江噪声样本数的增加的变化情况,图2(e)、(f)绘制了2段数据其相应的统计分布直方图并分别用Alpha分布和高斯分布对冰下噪声数据进行了拟合。图2(e)中高斯分布的均值μ=0、方差δ=0.211 1,采用分数阶矩法估计噪声数据获得的Alpha稳定分布的参数α=1.661 7、γ=0.245 8。图2(f)中高斯分布的均值μ=0、方差δ=0.274 4,采用分数阶矩法估计噪声数据获得的Alpha稳定分布的参数α=1.600 5、γ=0.268 5。图2(g)、(h)分别对应松花江两段噪声的频谱情况,可知能量主要集中在低频部分。 图3描述了北极冰下噪声数据及拟合情况。图3中,(a)、(b)是在北极冰下噪声数据时域图,图3(c)、(d) 描述了样本方差随北极噪声样本数的增加的变化情况,图3(e)、(f)绘制了2段数据其相应的统计分布直方图并分别用Alpha分布和高斯分布对冰下噪声数据进行了拟合。图3(e)中高斯分布的均值μ=0、方差δ=0.126 8,采用分数阶矩法估计噪声数据获得的Alpha稳定分布的参数α=1.721 7、γ=0.188 2。图3(f)中高斯分布的均值μ=0、方差δ=0.093 3,采用分数阶矩法估计噪声数据获得的Alpha稳定分布的参数α=1.825 1、γ=0.186 0,图3(g)、(h)分别对应北极2段噪声的频谱情况,能量主要集中在低频部分,相比于松花江噪声,北极冰下噪声在低频部分的能量更加集中。 根据图2、3(c)、(d)及估计出的分布参数可以看出:噪声数据的样本方差随噪声样本数的增加不收敛于常数,根据文献[15]可知松花江冰下噪声和北极冰下噪声均为非高斯分布;表2描述了噪声数据对应的峰度值和偏度值,从冰下噪声的峰度值亦可知冰下噪声为非高斯分布且具有冲击特性,从偏度值可知冰下噪声数据分布大致符合对称分布;对冰下噪声数据的拟合时,Alpha稳定分布拟合效果明显优于高斯分布,Alpha稳定分布更加贴近于冰下噪声实际情况。 表2 冰下噪声的偏度和峰度Table 2 Skewness and kurtosis of under ice noise 图4、5描述松花江和北极2种冰下噪声在不同频段条件下的统计和拟合情况,从图4、5(a)、(b)中看出,1~10 kHz的噪声能量比较大,对比图4、5(c)、(d),可知随着频率的提高,噪声的能量逐渐减小,即噪声能量主要集中在低频段范围内。 图2 松花江冰下噪声数据统计及拟合Fig.2 Statistics and fitting of under ice noise data of Songhua River 根据冰下噪声的脉冲特性以及Alpha稳定分布的拟合情况,根据2.3节可基于不同参数的Alpha稳定分布仿真出的冰下噪声用来研究对匹配滤波器检测性能的影响因素。图6是令参数β=0,δ=0,改变参数α、γ仿真得到的服从Alpha稳定分布的冰下噪声。 采用第8次北极科考采集的冰下噪声数据和松花江冰下噪声数据(采样频率fs=50 kHz)为噪声背景,选取噪声数据时宽为20 ms,采用CW和线性调频脉冲信号与实际噪声叠加后作为接收信号进行匹配滤波检测,绘制相应的ROC曲线,分析检测性能。检测性能分析过程如2.2节所示。实验中设置CW信号的频率为1 kHz,脉宽为20 ms,LFM信号的起始频率为1 kHz,带宽为4 kHz,脉宽为20 ms。 图3 北极冰下噪声数据统计及拟合Fig.3 Statistics and fitting of under ice noise data of Arctic 图7(a)、(c)描述了不同SNR下CW信号在松花江噪声背景和北极噪声背景下的检测情况,图7(b)、(d)描述了不同SNR下LFM信号在松花江噪声背景和北极噪声背景下的检测情况。从4幅图中都可以看出随着SNR的增加,对信号的检测性能增强。表3中,虚警概率固定为5%,在松花江和北极冰下噪声下的LFM信号和CW信号的检测概率可以看出,2种背景噪声下对LFM信号的检测能力比对CW信号的检测情况要好得多,CW信号的检测对SNR的要求比LFM信号的检测高,在低信噪比的情况下, CW的检测能力很差, LFM的检测情况较好。 图4 不同频段下松花江冰下噪声1的统计及拟合Fig.4 Statistics and fitting of under ice noise data 1 of Songhua River at different frequency bands 图5 不同频段下北极冰下噪声数据1的统计及拟合Fig.5 Statistics and fitting of under ice noise data 1 of Arctic at different frequency bands 图6 服从Alpha稳定分布的冰下噪声Fig.6 Under ice noise with Alpha stable distribution 图7 不同情形下匹配滤波检测性能Fig.7 Matched filter detection performance in different situations 通过仿真生成采样频率fs=50 kHz,符合Alpha稳定分布的随机变量作为冰下噪声数据,根据Alpha稳定分布统计参数生成不同噪声背景,研究参数对检测性能的影响。控制信噪比SNR=-16 dB,改变Alpha稳定分布的参数α生成对应的冰下噪声数据,与LFM信号叠加后,采用匹配滤波进行检测并作ROC曲线图分析其检测性能。LFM信号的起始频率为1 kHz,带宽为4 kHz,脉宽为20 ms。设定Alpha稳定分布的参数β=0,γ=1,δ=0,α的数值依次为0.4、0.6、1.0、1.4、1.6、2.0,生成冰下噪声数据,得到不同特征指数α对应的ROC曲线;设定Alpha稳定分布的参数α=1.0,β=0,δ=0,γ的数值依次为0.2、0.4、0.6、0.8、1.0,生成冰下噪声数据,得到不同尺度参数γ对应的ROC曲线;根据1.2节,当α的数值固定为2.0时,此时的Alpha稳定分布即为高斯分布。以下对应不同噪声背景下对LFM信号检测的ROC曲线。 图8(a)描述了不同特征指数α对应的LFM信号检测情况,图8(b)描述了虚警概率为5%时各参数所对应的检测概率,可以看出随着α的逐渐增加,检测概率随之降低,检测能力下降,也说明了采用高斯分布生成的变量作为冰下噪声数据会对检测性能产生一定的影响; 图8(c)描述了不同尺度参数γ对应的LFM信号检测情况,图8(d)描述了虚警概率为5%时各参数所对应的检测概率,可以得到随着γ的逐渐增加,检测概率浮动较小,对检测性能的影响较小。 表3虚警概率5%时检测情况统计表 Table3Statisticaltableofdetectionwhenfalsealarmprobabilityis5% 接收信号信噪比/dB检测概率/%接收信号信噪比/dB检测概率/%松花江噪声+CW信号北极噪声+CW信号-899.1-1097.1-1289.2-1462.5-1628.9-898.8-1093.3-1273.0-1441.1-1616.1松花江噪声+LFM信号北极噪声+LFM信号-12100.0-1499.4-1691.8-1849.3-2013.1-18100-20100-2297.1-2477.5-2553.5 1) 北极噪声和松花江噪声数据的统计特性都具有非高斯特性,且偏度在0附近,基本上满足对称分布;本次收集的松花江噪声数据的峰度值略大于北极噪声数据的峰度值,北极噪声数据估计得的α数值大于松花江噪声数据估计的数值。 2) 在统计特性方面,采用Alpha稳定分布建模的北极噪声和松花江噪声数据相比于高斯噪声,更加贴近于冰下噪声实际情况。 3) 在本次收集的北极和松花江冰下噪声数据下对不同的信号形式及参数的检测性能分析发现,匹配滤波器对LFM信号的检测能力优于CW信号;信噪比相同的情形下,随着Alpha稳定分布参数α的逐渐增加,对信号的检测能力逐渐减弱。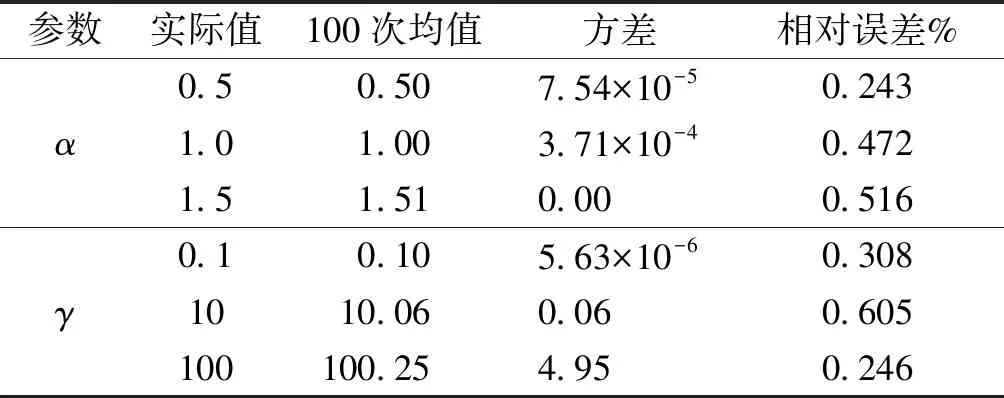
1.5 峰度和偏度
2 匹配滤波检测性能分析方法
2.1 匹配滤波器
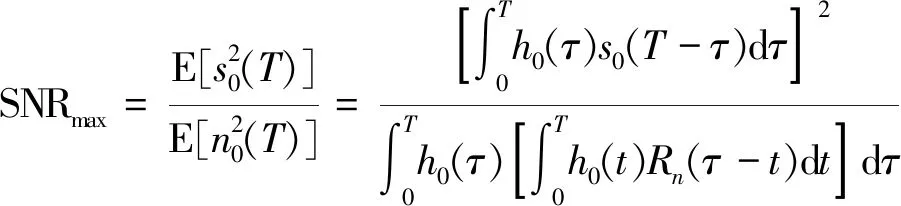

2.2 检测性能分析流程
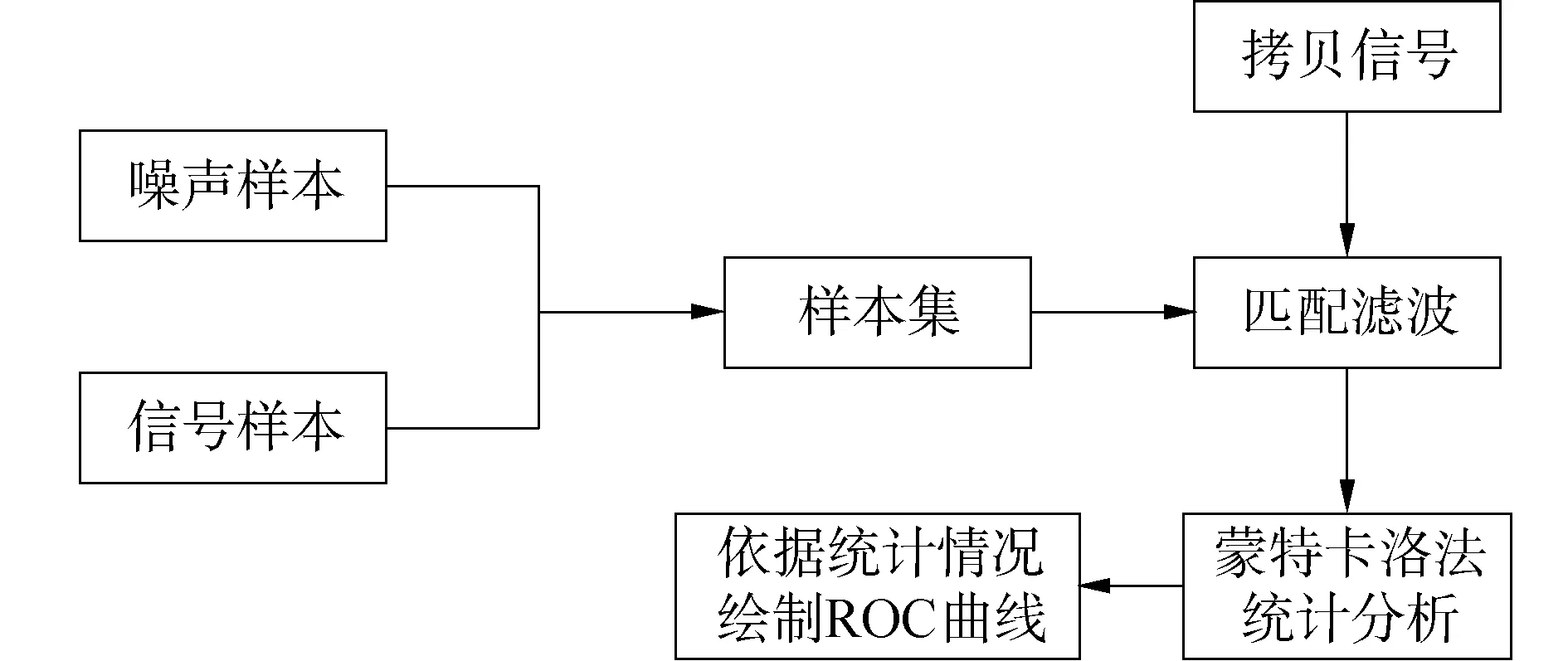
3 实际数据及仿真实验研究
3.1 冰下噪声数据特性分析
3.2 基于Alpha稳定分布仿真冰下噪声
3.3 实际冰下噪声匹配滤波器检测性能分析

3.4 不同参数对检测性能的影响
4 结论

