多通道烘缸水平通道内蒸汽凝结换热的研究

乔丽洁 董继先， 杨琸之 刘 欢 王 莎 董 岩

（1.陕西科技大学机电工程学院，陕西西安，710021；2.中国民用航空飞行学院飞行技术学院，四川广汉，618307）

传统烘缸干燥纸张的热量主要来源是蒸汽凝结释放的大量潜热，但烘缸内部蒸汽凝结水的积聚是阻碍热量有效传递的重要问题之一。多通道烘缸作为一种新型烘缸，旨在解决烘缸内凝结水严重积聚的问题[1]，其结构如图1 所示。蒸汽在烘缸内壁被限制在轴向分布的小通道内流动，凝结水被不断通入的蒸汽推出烘缸，解决了烘缸内冷凝水积聚的问题。与传统烘缸相比，其凝结水换热系数比传统烘缸大了7～20倍[2]。但是由于蒸汽凝结水的产生，小通道中形成了气液两相混合流，其换热特性相对复杂[2-3]。

多通道烘缸的干燥效率主要受到通道内蒸汽凝结特性的影响[2-4]，因此分析蒸汽凝结特性对于提高换热性能具有重要意义[5-7]。Xin 等人[8]、Cheng 等人[9]和Ma等人[10]研究了水平通道内凝结换热系数的影响因素。然而，在前人的研究中，冷却侧流体的参数对凝结换热的贡献往往被忽略。蒸汽侧热量来源是蒸汽，所以用蒸汽质量通量来表示换热系数非常恰当；而冷却水侧的冷却水雷诺数（Rec）对于确定凝结换热的效果很重要，所以可用冷却水雷诺数（Rec）的变化表示凝结换热系数的变化趋势[10]。Cheng 等人[9]和Ma 等人[10]研究了在充满蒸汽/氮气混合物的矩形通道内，冷却水雷诺数（Rec）、蒸汽质量通量等因素对蒸汽凝结换热系数的影响；结果表明，蒸汽凝结换热系数随着Rec和蒸汽质量通量的增加而增加。对于多通道烘缸通道内的凝结过程，Rec反映了冷却水的湍流程度，因此对Rec的研究意义重大。因为通过调节湍流度可以促进对流换热，所以冷却水的湍流越充分，侧冷却水的对流换热效果就越好，换热就越及时。

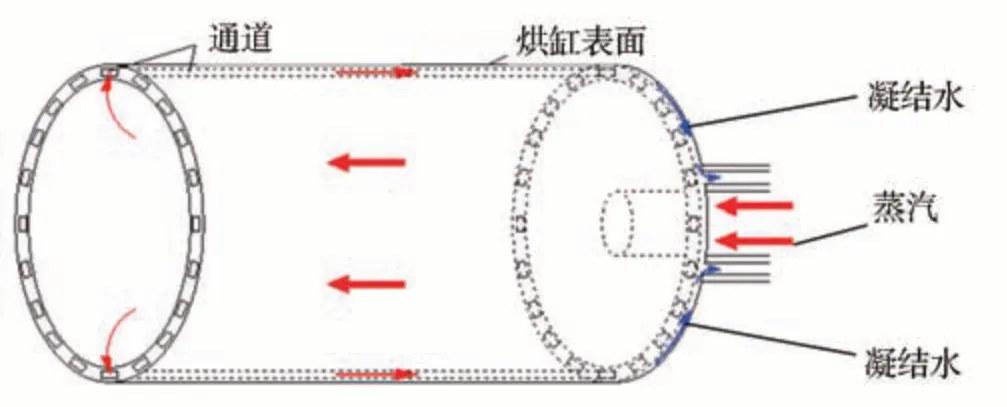
图1 多通道烘缸结构示意图Fig.1 Multi-channel cylinder dryer structure

凝结换热系数能够直接体现凝结换热的效果，通常采用多个特征数表示凝结换热系数，随之用得到的关联式计算凝结换热系数，再与实验值进行对比获得误差较小的数据，以此来确定能够预测凝结换热系数的关联式。前人研究得到的关联式主要基于2 种理论：两相乘子理论和边界层理论。实验条件相近与否是选择关联式的关键，基于2 种理论的众多关联式中，都有与本实验条件相近的关联式。基于两相乘子理论的关联式里最为经典的是Shah 等人[11]于1979 年提出的，适用于水平管、垂直管和倾斜管的通用关联式；同样基于两相乘子理论的关联式有：Akers 和Rosson(1960)关联式[12]，以及在Akers 和Rosson 关联式基础上修正了之后的Tandon(1995)关联式[13]与Dobson和Chato(1998)关联式[14]。基于边界层理论的关联式有Cavallini 和Zecchin(1974)关联式[15]，以及Moser 关联式[16]、Wang关联式[17]和Qu关联式[18]，这4个关联式的实验条件也与本研究相近，旨在研究带有四面冷却的圆形管或矩形通道中进行均匀周向冷却的过程。基于这4 个关联式的实验通道尺度均与本研究的实验相似，选择Shah(1979)关联式、Tandon(1995)关联式、Dobson、Chato(1998)关联式及Cavallini 和Zecchin(1974)关联式来描述多通道烘缸水平通道内蒸汽的凝结关系。本研究的主要目的是探究蒸汽在水平通道内的流动凝结换热特性，分析了蒸汽质量通量、冷却水雷诺数对凝结换热系数的影响；并通过与现有常用关联式的对比，确定能够恰当描述多通道烘缸水平通道内蒸汽凝结关系的关联式。

1 实验系统

1.1 实验装置

本研究的实验装置如图2 所示，包括3 个主要部分：测试段、蒸汽回路和冷却水回路。测试段是实验系统的核心，其中蒸汽凝结并释放热量至冷却水，冷却水在其回路中循环，并以间壁式换热方式冷却测试段中的蒸汽。

测试段结构示意图如图3 所示。从图3 可见，测试段由3块板组成，采用螺栓连接，其中间板是用铝板铣削而成，两侧开有平行的矩形通道；在两平行通道中的蒸汽和冷却水相向流动。蒸汽通道用透明的石英玻璃板覆盖便于观察，而冷却水通道用不锈钢板覆盖加以密封。实验系统非可视段隔热良好，可有效防止热量散失。通道的有效长度为800 mm，如图3(b)所示，蒸汽通道横截面的高度和宽度分别为4.5 mm 和13.5 mm。

系统中温度和压力采用热电偶（T 型：-200～350℃）和压力计测量。在2 个通道的入口和出口分别安装了4 个热电偶。冷却水温度通过沿通道以100 mm 间隔布置的7个热电偶进行测量，并将6个热电偶以140 mm 的间隔均匀地嵌入两通道间的金属壁中以测量壁面温度。1 个压力变送器（PX409-150GV：0~1034 kPa）用于测量蒸汽入口压力，1 个差压变送器（PX409-2.5GI：0~17.2 kPa）用于测量蒸汽侧的压降，2 个涡轮流量计分别用于测量蒸汽流量（FTB-1411：2.3~11.3 LPM） 和冷却剂流量（FLR1009-BR-D：50~500 LPM）。另外，数据采集仪（LR8400，日本，HIOKI）每20 ms 记录1 次截面中的温度、压力和流量，并在稳态条件下测量所有实验数据点。

1.2 实验数据处理

1.2.1 平均凝结换热系数

冷却水吸收的热量通过冷水通道内的热平衡确定，如式(1)所示。

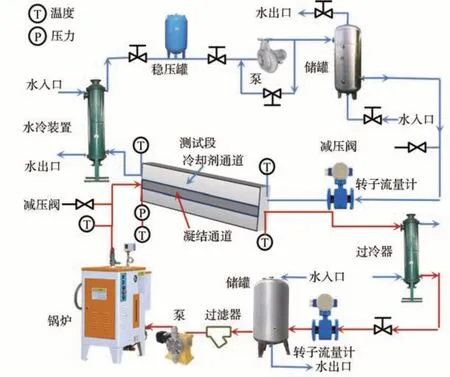
图2 实验装置示意图Fig.2 Experimental setup

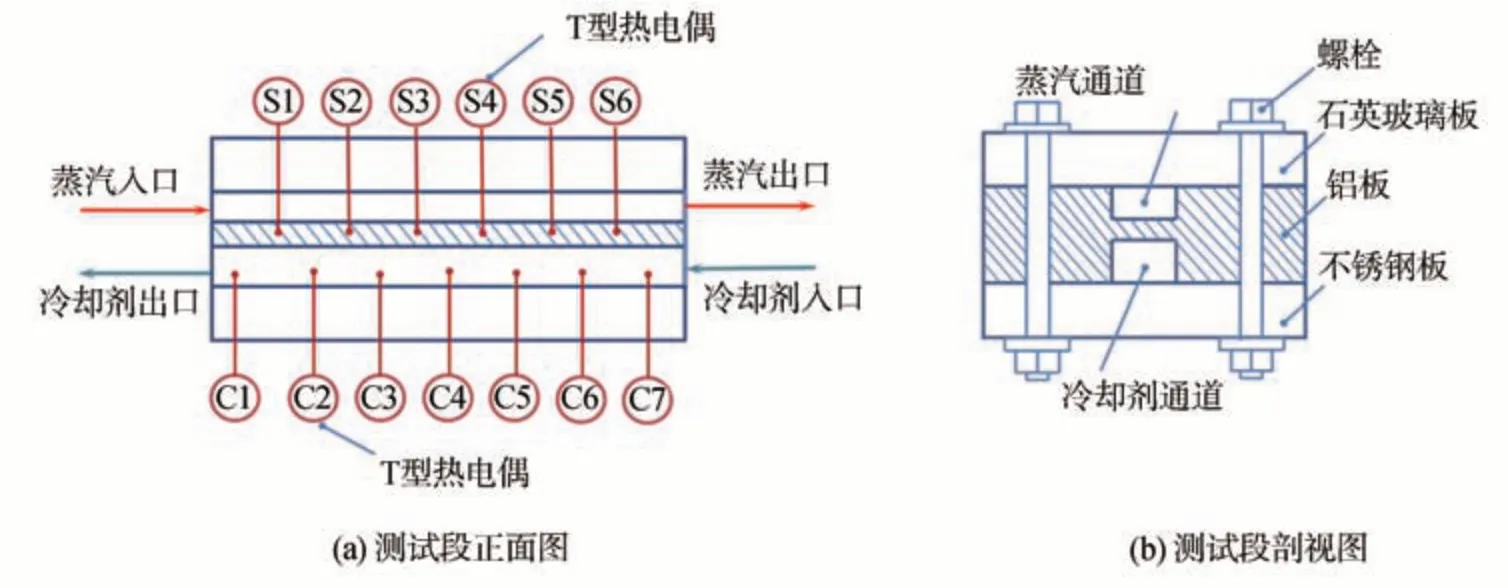
图3 测试段结构示意图Fig.3 Test section

式中，Qc是冷却水吸收的热量，W；Cp是冷却水的比热，J/(kg·K)；mc是冷却水的质量流量，kg/s；Tco和Tci分别是冷却水的出口和入口温度，K。

蒸汽释放的热量计算如式(2)所示。

式中，Qs是蒸汽释放的热量，W；A是传热的表面积，m2；hs是蒸汽通道的平均冷凝传热系数，W/(m2·K)；Ts是平均蒸汽温度，K；Tw是蒸汽通道和冷却水通道之间的壁面平均温度，K。

当吸收的热量和释放的热量间的热平衡差异在±10%以内时，才认为实验数据可信。本实验中，2个通道之间的传热率可以视为冷却水吸收的热量。

冷却水在不发生相变的情况下流动，并且冷却水的雷诺数（Rec）在实验期间从2.0×103变为1.2×104。Rec的计算如式(3)所示。

式中，Rec为冷却水雷诺数，无量纲；ρc为冷却水的密度，kg/m3；μc为冷却水的密度和运动黏度，kg/(m·s)；dc为冷却水通道的特征尺寸，采用与通道水力半径相等的圆管直径计算，m；uc为冷却水的流动速度，m/s。

通过测量第i段所对应的蒸汽平均温度以及壁面平均温度，可以计算得出第i段局部凝结换热系数，从而得到整个通道内的平均凝结换热系数，如式(4)所示。

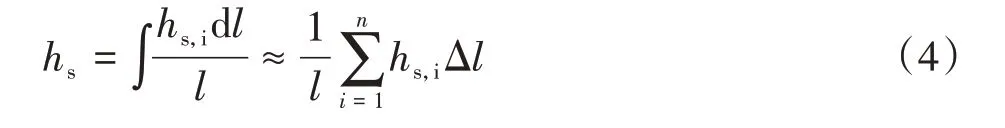
式中，hs平均凝结换热系数，W/(m2·K)；hs,i是第i段局部凝结换热系数，W/(m2·K)；l是通道有效长度，m。

1.2.2 重要实验关联式与平均绝对偏差

针对多通道烘缸小通道内蒸汽凝结换热系数，将换热系数关联式的预测值与本实验值进行比较，评估它们的预测性能。本研究共选取了Shah(1979)[11]、Cavallini 和Zecchin(1974)[15]、Tandon(1995)[13]及Dobson 和Chato(1998)[14]4种关联式，是因为这4个关联式均为描述水平通道气液两相流凝结换热系数的典型关联式，且这4个关联式的实验通道尺度均与本实验相近。以下对4 个关联式简称为Shah 关联式、Tandon 关联式、Dobson 和Chato 关 联 式 以 及Cavallini 和Zecchin 关联式。

其中，Shah 关联式基于474 个数据点拟合得出，适用于水平管、垂直管和倾斜管的管内蒸汽凝结换热，其表达式如式(5)～式(8)所示。

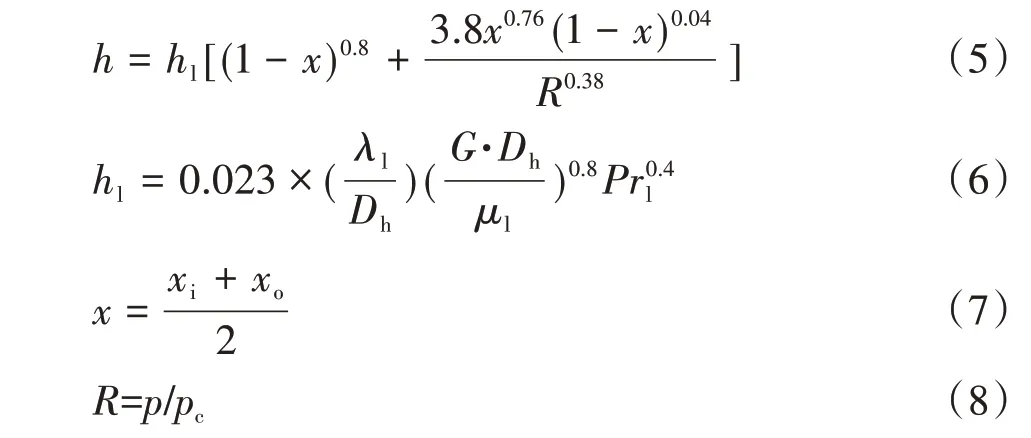
式中，h为气液两相流凝结换热系数，W/(m2·K)；hl为全液相换热系数，W/(m2·K)；x为蒸汽干度，取通道进、出口蒸汽干度平均值，%；xi为通道进口蒸汽干度，%；xo为通道出口蒸汽干度，%；λl为凝结液导热系数，W/(m·K)；Dh为通道水力直径，m；G为蒸汽质量通量，kg/(m2·s)；μl为凝结液动力黏度，Pa·s；Prl为凝结液普朗特数，无量纲；R为压缩因子，无量纲；p为实际压力，Pa，pc为临界压力，Pa。

Cavallini 和Zecchin 关联式是基于边界层、用于描述小通道环状流凝结水的换热关联式，表达式如式(9)所示。

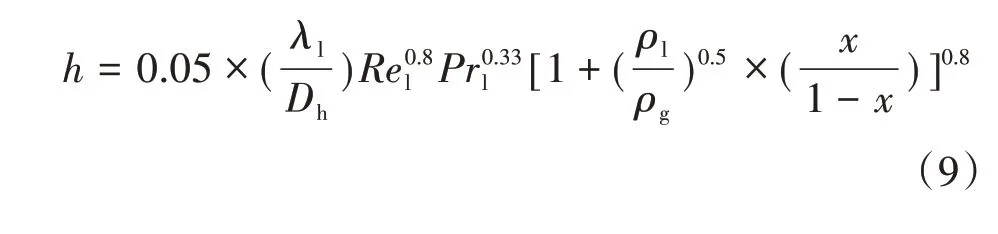
式中，Rel为冷凝水雷诺数，无量纲；ρl为冷凝水密度，kg/m3；ρg为蒸汽密度，kg/m3。

Tandon关联式依据制冷剂R12和R22在水平管中强制对流凝结的实验数据，基于对Akers-Rosson(1960)关联式的修正得出表达式，如式(10)所示。

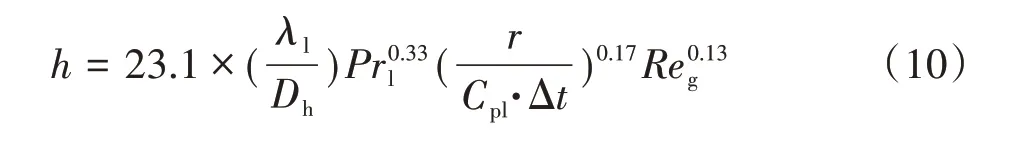
式中，r为汽化潜热，J/kg；Cpl为冷凝水比热，J/(kg·K)；Δt为冷凝水膜温度降，K；Reg为蒸汽雷诺数，无量纲。

Dobson 和Chato 关联式是在内径为3.14～7.04 mm的水平光滑圆形管内，对水和多种制冷剂（如R12等）进行凝结换热实验得到的，表达式如式(11)和式(12)所示。

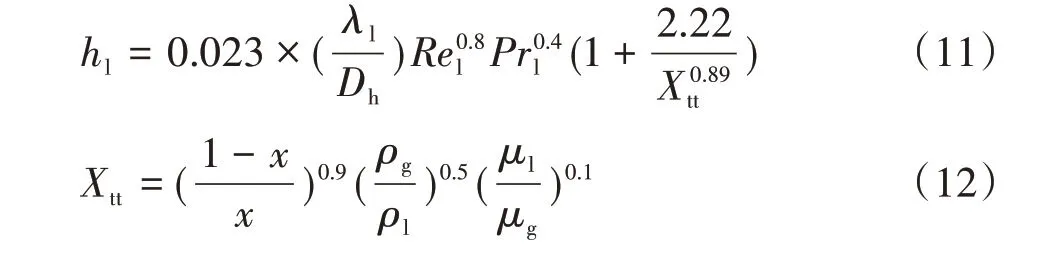
式中，Xtt为马蒂内里参数，无量纲；μg为蒸汽动力黏度，Pa·s。

将实验值与关联式的预测值对比时，评估参数为平均凝结换热系数（h）。主要使用2 个指标：误差带内数据百分比和平均绝对百分比偏差（mean absolute percentage error, MAPE）。误差带内数据百分比说明了处于一定误差范围内数据量的多少；MAPE 则说明一组数据自身的离散程度。MAPE 的定义如式(13)所示。

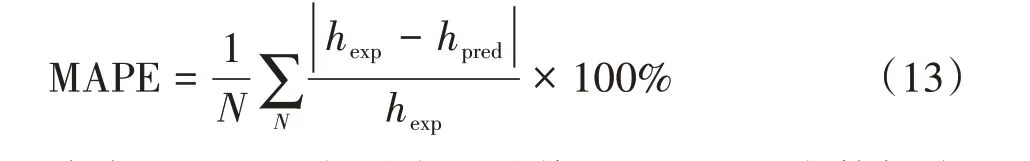
式中，MAPE 为平均绝对偏差，%；N为数据个数；hexp为凝结换热系数实验值；hpred为凝结换热系数预测值。

2 结果与讨论

2.1 换热量的变化

图4 所示为蒸汽质量通量（G）和冷却水雷诺数（Rec）对通道换热量的影响。从图4(a)可以发现，换热量随着G的增加而增加，且呈线性趋势，这是因为单位时间、单位通道截面面积通入的蒸汽质量越大，所携带的热量越多，通道内的换热量，必然呈现增加的趋势。图4(b)表明，随着Rec从1925.3 增加到11682.4，换热量增加了100.8%，Rec数值代表冷却水的湍流程度，Rec越大表明冷却水的湍流状态越强烈，而较强的湍流会促进冷却水通道的换热能力，故换热量得到提高。

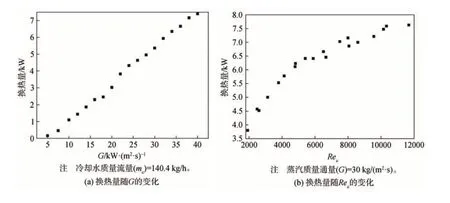
图4 蒸汽质量通量（G）和冷却水雷诺数（Rec）对通道换热量的影响Fig.4 The influence of steam mass flux（G）and cooling water reynolds number（Rec）on channel heat exchange

2.2 蒸汽质量通量对凝结换热系数的影响

蒸汽在多通道烘缸中凝结并释放热量，然后将热量传递到覆盖烘缸壁外部的湿纸幅上以干燥纸张。显然，蒸汽的质量流量直接反映了热量的消耗。前人的研究表明[5-7]，蒸汽质量通量（G）是影响水平通道传热的重要因素。

图5 为凝结换热系数随G的变化，图5 显示出平均凝结换热系数随G的增加而增加。图6 为温差与热流密度随G的变化；图6 显示出G的增加引起了较大的温度差和热流密度变化。一方面，随着G从5 kg/(m2·s)增加到24 kg/(m2·s)，平均热流密度增加，而平均温度差降低，根据傅里叶定律，平均凝结换热系数应增加；另一方面，随着G从24 kg/(m2·s)增加到40 kg/(m2·s)，平均热流密度增加了71.3%，但平均温度差却增加了30.5%。显然，热流密度的增幅比温度差的增幅更大，这一增幅仍然导致了平均凝结换热系数的增加；但是值得注意的是，这个阶段平均凝结换热系数的增长趋势相对较慢。最终可以得出结论，G的增加会获得更好的换热性能。

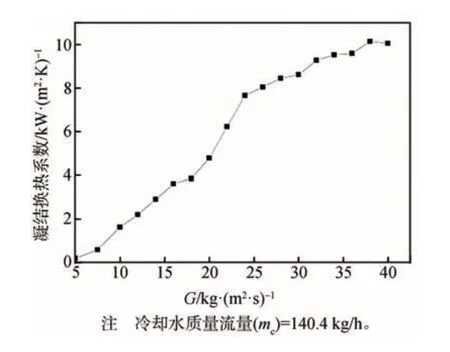
图5 凝结换热系数随G的变化Fig.5 Variation of condensation heat transfer coefficient with steam mass flux（G）

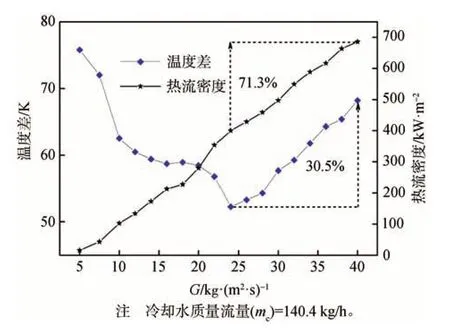
图6 温差与热流密度随G的变化Fig.6 Variation of temperature difference and heat flux with steam mass flux（G）

值得关注的是，本实验的结果与Yan 等人[7]的结果呈现相同的趋势。在Yan 等人的研究中，当G为20～40 kg/(m2·s)时，大部分质量通量区域常会出现团状流和波状流。因此，当G为24 kg/(m2·s)时，团状流和波状流增加了蒸汽相的扰动，从而增加了两相界面之间的相对表面粗糙度，并相应地增加了蒸汽和凝结水之间的摩擦，导致更大的两相流压降。如果蒸汽凝结过程中的两相流压降较大，则表明在通道中进行热传递期间蒸汽克服的摩擦阻力越大，则消耗的能量就越多。可以想象，对于多通道烘缸来说，干燥纸张需要更多能量。因此，选择蒸汽质量通量为24 kg/(m2·s)时可以避免压力降过大。

2.3 冷却水雷诺数对凝结换热系数的影响

冷却水雷诺数（Rec）反映了冷却水的湍流程度，而通过调节湍流程度可以促进冷却水侧对流换热，所以对Rec的研究意义重大。冷却水的湍流越充分，对流换热就越好。因此Rec的变化能够表示凝结换热系数的变化。

图7为凝结换热系数随Rec的变化，图7显示出凝结换热系数随Rec的增加而增加。图8 为温度差与热流密度随Rec的变化。从图8 可知，随着Rec从1925.3增加到11682.4，热流密度增加了101%，但温度差增加了81%。因此，按照傅里叶定律，热流密度的增加要快于温度差的增加，这显然会导致凝结换热系数的增加。但由于Rec的变化较大，可以看出冷却水的凝结换热系数发生了波动。这种波动是由于随着Rec的较大变化，流体经历了层流、过渡流、湍流和充分发展的湍流，从而导致了极不稳定的流场。这种不稳定性使金属壁表面和冷却水间的剪切作用有时很强，有时很弱。一方面，当剪切作用较强时，由湍流引起的热传递得到增强；另一方面，当剪切作用弱时，冷却水层变厚，导致热阻增加并且传热减弱。综上可知，随着Rec的增加，凝结换热系数呈现增加的趋势。

2.4 实验值与经典关联式预测值的对比

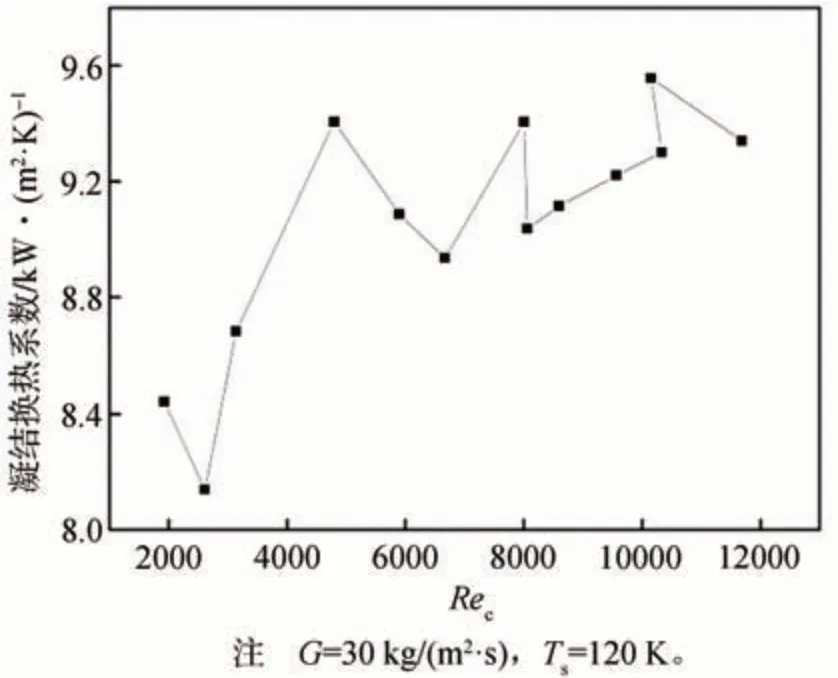
图7 凝结换热系数随Rec的变化Fig.7 Variation trend of condensation heat transfer coefficient with Rec of cooling water

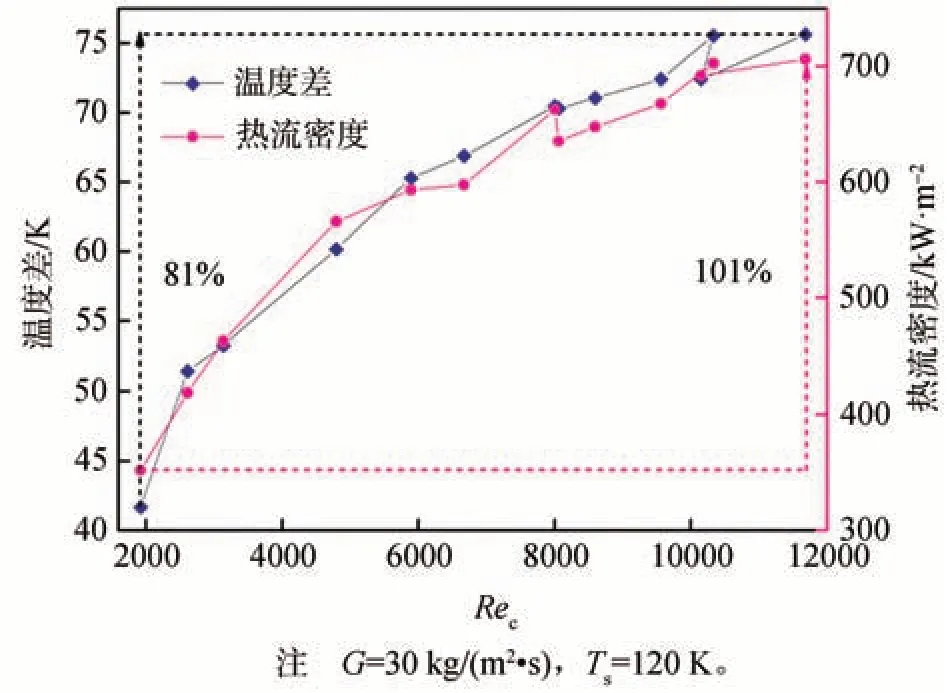
图8 温差与热流密度随Rec的变化Fig.8 Variation of temperature difference and heat flux with Rec of cooling water

图9 为凝结换热系数实验值与主要关联式预测值的对比。由图9(a)可以看出，Shah 关联式预测值的平均绝对百分比偏差（MAPE）为28.6%，预测值在±30%和±40%误差带范围内的数据百分比分别为71.7%和78.3%（±40%的数据作为参考，因此图中均仅画出了±30%的数据），有17.4%的数据为负偏差，说明此关联式偏差分布均匀，且总体偏小。对比Shah 关联式和实验条件发现，Shah 关联式是针对水力直径为7～40 mm 的光滑宏观通道内蒸汽凝结而建立，与本实验通道的尺度最为接近。且本实验条件与Shah 关联式中的4个关键参数的范围全部相符：饱和温度Ts为294～583 K，蒸汽干度为0～100%，蒸汽质量流量为10.83～210.6 kg/(m2·s)，热流密度为158～1.89×106W/m2，因此，Shah 关联式对凝结换热系数的预测较为准确。

由图9(b)可以看出，Cavallini 和Zecchin 关联式预测值的MAPE 为42.7%，预测值在±30%和±40%误差带范围内的数据百分比分别为26.1%和47.8%，有9.8%的数据为负偏差，说明此关联式偏差较大，而且预测值普遍高于实验值。这主要是因为Cavallini 和Zecchin 关联式主要针对光滑圆形管道建立的，而本实验通道截面为矩形，截面形状是影响气液两相流凝结换热的主要因素之一[16]，因此，会造成此关联式与实验值之间的差异。

由图9(c)可以看出，Dobson 和Chato 关联式预测值的MAPE 为56.9%，预测值在±30%和±40%误差带范围内的数据百分比分别为26.1%和76.1%，仅有3.9%的数据为负偏差，说明此关联式比Cavallini 和Zecchin 关联式的预测值偏差大，而且预测值偏高。Dobson 和Chato 关联式主要是针对制冷剂（R12、R22、R134a、R32/R125）建立的，没有考虑蒸汽凝结的情况，因而与本实验的蒸汽有差异。通道内介质的种类很关键，不同介质的物理性质、热力学性质均有很大不同，因此，在建立关联式时，一定要注意通道内介质的种类。

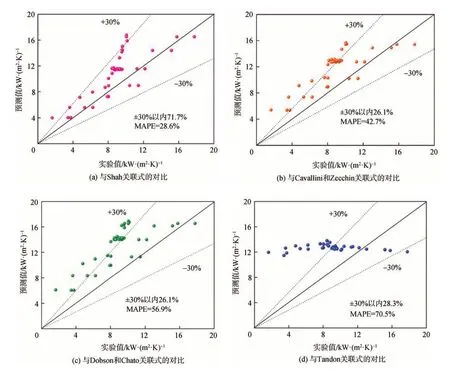
图9 凝结换热系数实验值与现有主要关联式预测值的对比Fig.9 Comparison of the experimental value of condensation heat transfer coefficient and the predicted value of the main correlation equation

由图9(d)可以看出，Tandon 关联式预测值的MAPE在4个关联式中最大，达70.5%，预测值在±30%和±40%误差带范围内的数据百分比分别为28.3%和58.7%，有7.8%的数据为负偏差，说明此关联式预测值偏大。Tandon 关联式主要是针对制冷剂（R12、R22、R134a、R32/R125）建立，与本实验的蒸汽有明显差异。另外，Tandon 关联式采用的介质质量通量为175～560 kg/(m2·s)，而本实验的蒸汽质量通量低于50 kg/(m2·s)，二者有明显的不同。

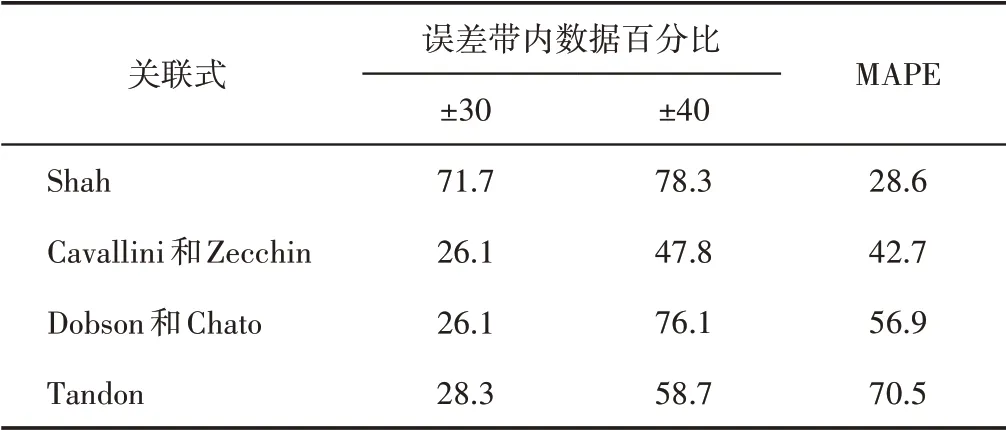
表1 4个关联式的性能评估Table 1 Performance evaluation of 4 correlations %

表1 列出了4个关联式的性能评估。由表1可见，4 个关联式虽然都适合小通道尺度的蒸汽凝结情况，但是对于蒸汽凝结换热系数的实验数据预测值的MAPE 由低到高分别为：Shah（28.6%）

综上，经典的Shah 关联式具有小于30%的预测误差，说明其对通道内蒸汽凝结换热系数具有较高的预测精度，也从侧面证实凝结换热系数实验数据的可靠性；Shah关联式在4个关联式中的预测精度最高。

3 结论

本研究通过实验分析了蒸汽在多通道烘缸通道内蒸汽的凝结换热特性，采用现有凝结换热关联式对凝结换热系数进行计算（预测值）并与本实验值进行了对比分析。

3.1 通道内换热量会随着蒸汽质量通量的增加而增加，且呈线性趋势；通道内换热量随着冷却水雷诺数的增加而增加，说明冷却水通道中的换热能力会随着换热量的增加而更强。

3.2 蒸汽质量通量的增加会获得更好的换热性能，选择合理的蒸汽质量通量（为24 kg/(m2·s)）可以避免压力降过大；随着冷却水雷诺数增加，热流密度的增长率始终高于传热温度差的增长率，所以凝结换热系数的总体趋势增加；凝结换热系数的波动是由于冷却水雷诺数的变化引起流动状态的不稳定，从而对换热造成影响。

3.3 Shah(1979)关联式对多通道烘缸通道内蒸汽凝结的实验数据预测最好；Cavallini 和Zecchin(1974)关联式、Dobson 和Chato(1998)关联式及Tandon(1995)关联式对通道内蒸汽凝结的实验数据不能进行准确预测。