基于改进蚁群算法的飞机航路规划研究

梁洁雅，田卫萍，杨志坚

（北方自动控制技术研究所，太原 030006）

0 引言

由于战场环境复杂多变，飞机航路规划问题是飞机执行作战任务时需要提前规划的基本问题［1］。航路规划在飞机实施作战任务中有至关重要的作用，能够在紧急作战情况下，生成快速有效的航线，从而顺利完成突防、侦察、搜救等任务。

关于飞行区域内的航路规划算法，有众多研究成果，航路规划算法大约分为3 类：基于确定性搜索、基于概率型随机搜索和基于计算规划方法［2］。基于确定性搜索的方法一般化为成本最小化问题，如时间成本最小化或航线里程长短最小化，具体算法有A*算法、动态规划法［3］、RRT 快速扩展随机树［4］；基于随机搜索算法有模拟退火方法［5］、遗传算法和蚁群算法，三者都属于全局型的概率搜索算法；基于计算的规划方法包括利用电荷之间作用力产生人工势场法和神经网络算法［6］等。学者宋雪倩等［7］结合A*和Dubins路径的思想，为无人机构建由Dubins曲线组成的最短避障路径，但是A*算法最终最优程度取决于启发函数以及加权因子的选取，从发表文献来看，通常是通过试凑的方法来得到较合适的加权值。学者刘超［8］以航程作为性能指标，将无人机侦察多目标航路规划转化为多旅行商问题，基于遗传算法设计了有效的染色体编码和遗传算子，规划出合理有效的航路，但是遗传算法有一定的局限性：容易过早地收敛以及在进化后期搜索效率较低。学者魏勇等［9］提出了一种基于改进粒子群算法的机器人路径规划方法，将差分方法加入粒子群算法，但差分进化方法变异得到的个体有不在解空间的风险，不适用于飞机航线规划。学者曹良秋等［10］在遗传算法基础上，设计了能够根据任务需求为无人机规划出飞行航路算法，但该算法设计基础是二维平面的规划，无法满足三维飞行区域内的航路规划。人工势场法是通过电荷的相互作用进行规划，规划实时性好且时间短，适合于飞机的实时航路规划，但容易产生局部极小值问题和目标不可达问题［11］。

本文采用蚁群算法对特定飞行区域内的飞行任务进行航路规划，引入信息素动态更新机制，同时根据飞机机动性能的影响来调整航线拐角，通过MATLAB 软件对算法的航路规划结果进行仿真验证，试验结果表明，可以在航线规划时有效躲避威胁源并利用地形隐蔽作用生成航迹。

1 飞机航路规划问题描述

航路规划问题是一个涉及多专业的综合性复杂研究课题，在飞机飞行过程中，首先需要根据飞行区域的地形、地物和威胁信息进行飞行航路规划，航路规划是在复杂的战场环境下，搜索飞机从起点到终点符合飞机机动性能的最优航线，提高飞机任务完成效率［12］。航路规划需要解决以下3 个关键问题［2］：

1.1 地形信息的获取

地形信息是航路规划的基础，由于试验条件有限，很难获得高分辨率的卫星遥感数字地图，而模拟数字地图［13］能够模拟自然界中的山峰和盆地，因此，在仿真条件下，本算法采用模拟数字地图，为航路规划提供了方便。

1.2 威胁模型建立

威胁信息由先期侦察获得，建立在地形数据上，威胁能力由威胁中心和威胁半径确定。威胁模型的复杂程度确定飞机航路规划时选择威胁回避策略还是威胁突防策略。本算法假设敌威胁面积有限，故采用威胁回避策略。

1.3 航路规划算法的选择

航路规划算法能够在利用地形信息、威胁信息的基础上充分发挥计算机技术的优势，规划出高质量的航路。由于飞机的飞行任务区域范围较大，使用基于确定性搜索的方法在大范围内将导致数据暴增，优化时间过长，其巨大的信息处理量是计算机无法承受的；使用基于随机搜索的方法是以随机搜索的方式搜索全部解空间，可以跳出局部极小点去寻找全局最优值。因此，本文采用蚁群算法进行航路规划。

蚁群算法属于概率型随机搜索算法，广泛应用于路径搜索领域，1992 年由M.Dorigo 首先提出，称为蚁群系统。传统蚁群算法就是让人工蚂蚁在随机搜索的路径空间中随机行走，人工蚂蚁会选择信息素浓度较高的位置，作为下一次访问的路径点并在经过的路径上留下信息素，信息素的浓度与路径长短有直接相关性，经过多次迭代后，人工蚂蚁逐渐聚集到代表最优解的最短路径上，其他路径上的信息素逐渐挥发最终消失，最终蚂蚁会在信息素的正反馈作用下集中到最优路径上［14］。

但是传统蚁群算法在航路搜索过程中信息素计算模式不变，会导致在算法搜索过程中，所有蚂蚁过早地聚集到同一条觅食路径，这样显然不利于对最优解的进一步搜索，使算法陷入局部最优解而停止搜索。针对传统蚁群算法所存在的问题进行适应性改进，提出动态更新信息素大小机制，提高了全局航路搜索能力。

2 改进蚁群算法设计

2.1 飞行空间构建

飞机避障航路规划可以归结为在三维空间中航线规划的问题［15］，将地形高程数据映射到三维空间直角坐标系中，以飞机的作战任务区域建立坐标系，以飞机前进方向为x 轴，左右转弯方向为y 轴，纵向攀爬和俯冲方向为h 轴方向。障碍物通常为敌侦察和火力威胁信息，在威胁建模中，敌雷达侦察用红色球体表示，威胁范围为雷达侦察范围；敌火力威胁用蓝色球体表示，威胁范围为防空武器攻击范围。通常情况下，在威胁范围内，与敌威胁距离越大，威胁越弱。如果飞行区域处于敌方阵地范围，基本上被敌方防御系统所覆盖，则需要引入突防概率来判断飞机穿越规划空间后的生存概率。本算法对战场的想定为规划空间处于我方地域，敌威胁面积有限，飞机飞行时速度较快，可以很快绕过威胁区域，实现障碍回避，飞机航线规划空间如图1所示。

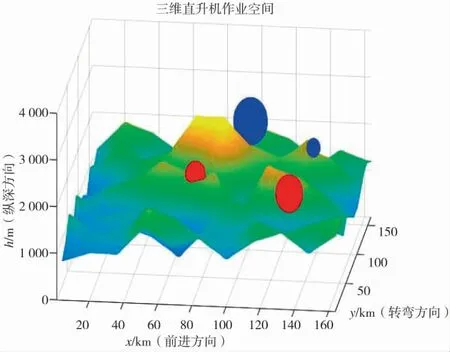
图1 飞机航线规划空间

在二维路径规划方法中，栅格法是常用的划分规划空间的方法，栅格法是将搜索空间平均划分成大小相等的栅格［16］。栅格大小决定了算法规划的精度和效率，栅格过大就会造成路径规划算法搜索范围减小，从而无法规划出最有效路径，栅格过小会造成算法搜索时间过长。因此，选取适当的大小是航线规划算法寻优和提高效率的关键。对于三维空间下的航路规划算法，同样能够使用栅格法来划分任务空间，航路规划算法采用按照坐标来划分栅格，以单元坐标作为单元栅格，即分别沿着规划空间的x，y，h 轴均匀划分为n 等份，每一等份代表可访问的航迹点，栅格位置使用规划空间的坐标表示。

2.2 航迹点选择

在规划空间中，x 轴作为前进方向，下一航迹点位于当前航迹点的x+L 方向上，L 为前进步长，步长L 决定了可选航迹点的集合大小，航迹点集合为Allow（x，y，h）={a1，a2，…an}。算法采用可变步长的搜索机制，具体方式为：在寻找下一航迹点时，根据预设的最大步长确定航迹点集合，通过信息素和启发值确定的转移概率选择最优航迹点，最优航迹点与当前位置的前进距离作为此次移动的步长。可变步长机制增加了航路搜索的灵活性和寻优能力，缩短了算法搜索时间，具体如图2 所示。

通过栅格法将三维规划空间划分成n3等份，每一等份都对应所在航迹点的信息素的值，信息素矩阵大小同样为n3，在航迹点集合Allow 中，通过转移概率确定下次访问的航迹点，转移概率Ps的公式为：

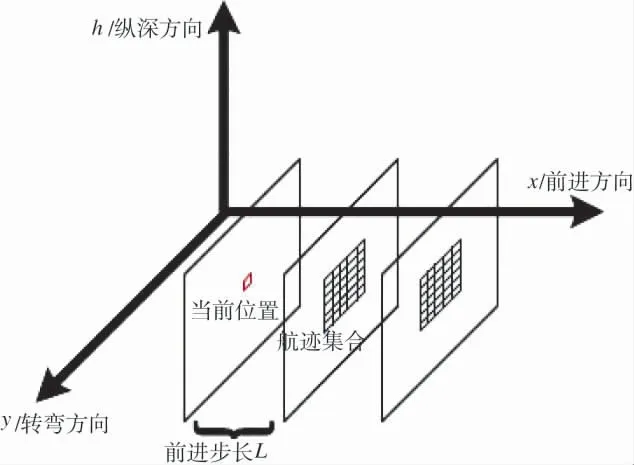
图2 可达轨迹点集合

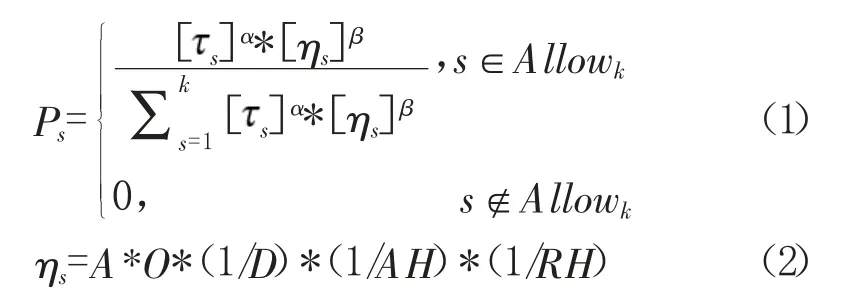
式（1）中，Allow 表示可访问的航迹点集合，s为栅格s 的信息素值，α 为信息素的重要程度因子，α 越大，表明信息素浓度在航迹点选择中的作用越大，ηs为栅格s 的启发值，β 为启发值的重要程度因子，β 越大，表明s 点的启发值在航迹点选择中的作用越大。Ps表明飞机从当前位置到s 点的期望概率。

式（2）为ηs的计算公式，其中A 为可达性因子，用于确定航迹点集合中的航迹点是否可达；O 为障碍物因子，使航迹点能够躲避敌武器威胁范围；D 为两个航迹点之间的距离，与启发值呈负相关，距离越大启发值越小；AH 为绝对高度，RH 为相对高度，通过相对高度和绝对高度判断航迹点与地形之间的关系，选择能够尽可能贴地飞行的航迹点。

2.3 信息素更新

2.3.1 信息素局部更新

信息素的更新与航路规划形成一个正反馈关系，当根据转移概率计算出下一个航迹点时，必须对该航迹点所处栅格位置的信息素进行局部更新，更新规则为：

2.3.2 信息素全局更新

当人工蚂蚁种群完成一次路径搜索后，由于信息素浓度的挥发作用，将规划空间中的信息素进行挥发调整，调整方式为=（1-ρ），其中，ρ 为挥发系数，然后从每只蚂蚁搜索到的路径path 中选取适应度值最高的路径，增加该路径上的每一个航迹点信息素浓度，提高下次蚁群迭代选择该路径的概率。适应度值计算方式为：

length 为航线总长度，Δheight为所有航迹点的相对高度和，控制算法选择贴地飞行的航路。适应度值越小，表明航路越好，对于最优路径信息素增加方式为：

其中，Q 为常数，表示蚂蚁迭代一次后释放的信息素含量，fitness表示航路的适应度值。

2.3.3 信息素的动态更新

信息素的更新方式确定了搜索航迹的效果，因此，当算法陷入收敛时，应当使用一定的手段跳出局部解以寻求更多的可能性，本文采用一种动态的信息素更新机制，更新过程为，若算法的最优解在t 代以内不发生改变时，使用以下公式更新信息素［17］：

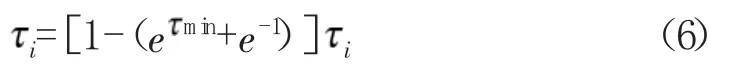
2.4 算法工作流程

改进蚁群算法的工作流程为：

算法1 改进蚁群算法Input：三维地图h（x，y，z），蚂蚁个数pop，迭代次数k，起点坐标start，终点坐标end O utput：最短航线bestpath 1.foreach i∈k do 2. foreach j∈pop do 3. curPoint=start 4. curPoint写入path 表5. forcurPointx 小于规划空间hx do 6. 可达航迹点集合A llow（x，y，h）={a1，a2，…an}7. foreach point∈A llow do 8. 使用启发函数η 计算转移概率Ps 9. 确定下一个航迹点nextPoint 10. end for 11. ifnextPointx 小于规划空间hx then 12. path←nextPoint 13. curPoint=nextPoint 14. 更新nextPoint信息素 s=（1-）images/BZ_74_849_2573_875_2609.png15. else 16. 终点end 写入path 17. curPoint=end 18. end if 19. end for 20. end for 21. 一次迭代完成，计算fitness，bestfitness 22. if t 代以内bestfitness没有变化then 23. 调整信息素增加求解可能性24. i=［1-（e min+e-1）］i 25. else 26. 增加最优路径信息素= +Δ 27.end for 28.输出path 中每次迭代适应度值最优的路径

3 仿真验证及结果分析

运用MATLAB 2019 对改进蚁群算法进行实现，仿真规划空间大小为160 km×160 km，高度为4 km，使用栅格划分法将空间分为41×41×41 的空间；蚂蚁种群pop=20，迭代次数为k=100，每一个栅格的初始信息素浓度=1，蚂蚁种群迭代一次后释放的信息素含量Q=100，信息素局部衰减系数为=0.5，全局迭代一次后信息素挥发系数为ρ=0.2，信息素重要程度因子取值α=3，航迹点启发值β=3，假设敌威胁范围为：

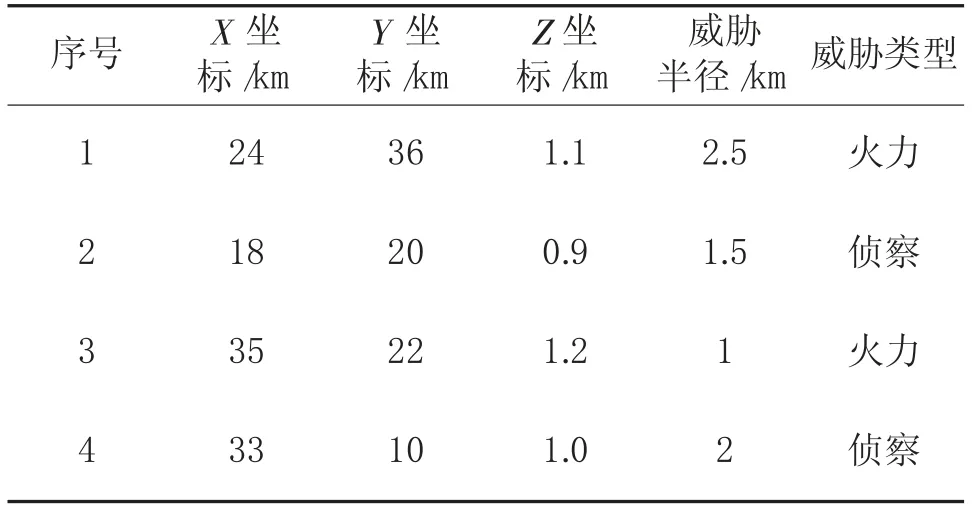
表1 障碍信息表

假设飞机航程满足的情况下，起点相同、终点不同、迭代次数相同时，改进后的算法和原算法的对比结果如表2 所示。

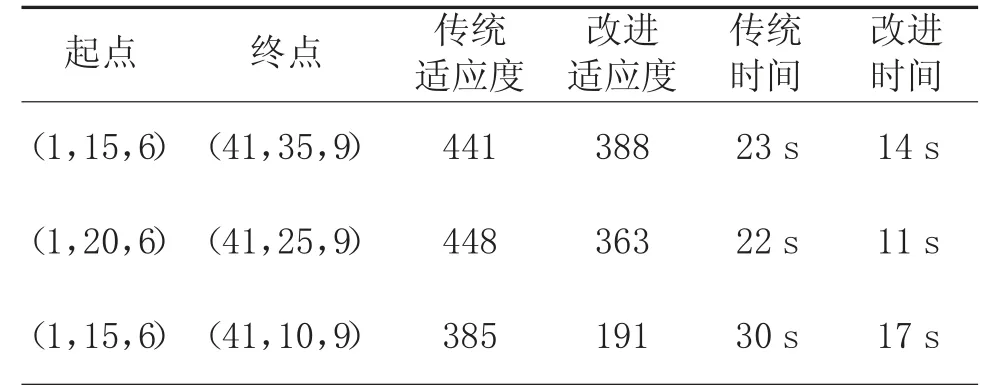
表2 算法结果比较

图3 改进算法的规划结果

其中，起点为（1，15，6），终点为（41，35，9）的规划结果如图3所示，图中虚线表示传统蚁群算法的规划路线，实线为改进后蚁群算法的规划路线。结果表明，改进后的蚁群算法能够更好地跟随地形规划航线，在适应度和规划时间方面都优于传统蚁群算法，航线起伏较小。适应度值变化趋势如图4所示，图中结果表明，传统蚁群算法的最优值在40 代收敛，但求解质量较差；改进后的算法能够不断寻找更多可行解，避免陷入局部最优解而导致过早收敛，最优适应度变化呈阶梯式下降，表明在最优航线不发生变化时，会启用信息素动态更新机制来帮助跳出局部最优解，求解效果明显优于传统蚁群算法。

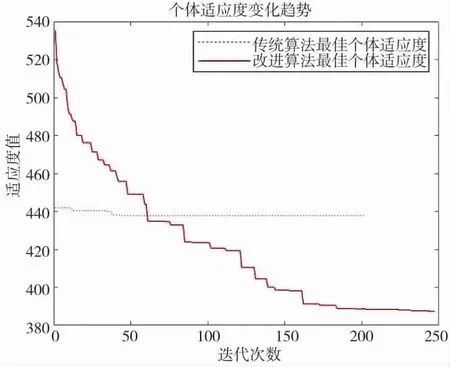
图4 适应度值

综上所述，改进后的航线规划算法能够在敌威胁范围有限情况下回避以绕行方式回避障碍物；能够进行地形跟随，利用地形优势来达到隐蔽作用；可以在较短时间内为飞机规划出可用的航路。

4 结论

本文提出了一种改进蚁群算法，该算法将飞机飞行空间定义为三维搜索空间，在三维搜索空间中规划航线，利用栅格法将三维空间均匀划n3等份，每一份代表一个的航迹点，最终规划的航线就是从起点栅格出发，依次连接相邻栅格直到终点栅格的最短路径。针对传统蚁群算法收敛过早和搜索速度慢的缺点，在传统算法的思想上增加了信息素动态更新机制，避免路径寻找陷入局部极小值，增加了算法的搜索空间以寻求最优航线，达到缩短求解时间，提高求解质量的效果。

航路规划问题是一个综合性的课题，仍然有许多方面进行深入研究，日后尚需进一步完善的任务有：

1）设计满足生存概率和突防概率的航路规划算法，在敌威胁较为密集，飞行区域被敌防御体系所覆盖时，能够使用威胁突防策略规划航路，以一定的突防概率穿越飞行空间，提高飞机生存概率；

2）建立更为复杂的威胁信息模型，侦察威胁需要充分考虑目标侦察概率的能力，而火力威胁需要充分考虑毁伤概率的影响；

3）设计实时航路规划算法，能够处理动态威胁信息并进行临机航路调整。