基于AKF 的AUV 对接回收组合导航研究*

包灵卉，曾庆军，朱志宇，戴晓强，赵 强

（江苏科技大学电子信息学院，江苏 镇江 212003）

0 引言

随着水下机器人的发展，我国对海洋的开发技术已达到世界前列。由于AUV 的运动灵活且范围大，国内外各科研机构多使用AUV 进行水下作业。而面对复杂的水下作业，AUV 需要多次返回支持平台，完成能源对接及数据交换等工作，以保证完成水下作业任务。精准导航是保证AUV 安全对接回收的重要条件，常用捷联惯性导航系统（Strapdown Inertial Navigation systems，SINS）作为主要的导航系统，由其他传感器作为辅助进行组合导航。但这种组合导航可能存在水下无信号或电磁波传播困难等问题，因此，水声定位逐步变成了各国海洋研究领域的热点［1-2］。超短基线定位系统（Ultra-Short Baseline，USBL）由于基阵尺寸小且使用范围广，被广泛应用于水下乃至深海导航定位［3］。

目前，在组合导航信息融合中，Sage-Husa 自适应卡尔曼滤波算法虽然可以实时估计噪声统计特性，但其滤波的收敛性差，达不到满意效果。文献［10］提出一种基于人工蜂群算法（ABC）改进的径向基函数（RBF）神经网络增强自适应无迹卡尔曼滤波算法（AUKF），但是其公式复杂，在实际情况下很难实现。文献［11］提出一种改进的自适应扩展卡尔曼滤波算法，只需要实时估计对滤波影响大的测量噪声协方差阵，但每个采样周期都对其进行估计，加深了计算的复杂度，滤波的实时性难以得到保障。

针对自主水下机器人的导航系统，采取了多传感器组合导航的方式，主要研究了AUV 进入声学作用范围时的基于USBL 辅助SINS 的组合导航，USBL 定位系统采用改进的高斯测距算法，解决了距离计算中存在的奇异情况，并结合SINS、DVL 和深度计等传感器建立改进的基于斜距的组合导航数学模型，然后设计了一种改进的自适应滤波算法，以简化的Sage-Husa 自适应滤波算法为框架，引入滤波收敛性判据及强跟踪滤波思想，在一定程度上改善了滤波收敛性和稳定性。而且通过仿真实验结合实际AUV 系统，证得AUV 导航系统采用改进的自适应滤波算法能安全回收。

1 AUV 对接回收中USBL 定位系统工作原理

在AUV 的对接回收过程中，对接流程分为4个阶段，分别为直线归位、直线跟踪、直线对接和惯性对接4 个阶段，重点研究的是USBL 作用范围内的组合导航，采用基于USBL 组合导航的方式进行导航，主要在直线归位阶段和直线跟踪阶段。在这个过程中，需要利用组合导航提供的速度、位置、姿态信息来调整AUV 与对接装置的位置，使得AUV在消耗能量较少的情况下，到达对接坞的中轴线上。在直线对接阶段，AUV 的重心已经行驶到中轴线上，且离对接口相距3 m~5 m，此时利用三维视场重建和视觉导航提供的相对位置和姿态信息来微调AUV 的状态，保证AUV 沿中轴线航行，且艏向角指向对接口。最后在惯性对接阶段，关闭所有推进器，依靠惯性驶入对接坞［6］。

图1 AUV 回收对接流程框图

USBL 定位系统由声学基阵和接收器或应答器组成，声学基阵安装在回收坞上，包括水听器和换能器，AUV 端为应答器。系统通过测定水听器的相位差来计算AUV 到回收坞的水平和垂直角度，再通过测定声波的传播时间来确定AUV 到回收坞的距离，最终得到AUV 相对于换能器的位置信息［7-8］。

图2 改进的高斯距离迭代原理图

采用纯距离定位的方法，由于纯距离定位法的定位方法是解算航迹的几何路径，由此获取距离量即可，只需要USBL 的测距功能，简化了系统的结构，并增强了系统的稳定性。纯距离定位法采用了改进的高斯距离迭代法，其步骤如下：

步骤1 将AUV 的航迹分割成若干条连接的直线段，初始直线段的初始点已知，在每条直线上的每个位置点测得AUV 到声源发射器的距离。

步骤2 将AUV 航迹中的一段与回收坞上声源发射器的位置信息放到二维平面上，形成一个二维平面关系图，设Ps点坐标为Ps（X0，Y0），任取AUV航迹上的3 个点p1（X1，Y1），p2（X2，Y2）和p3（x，y），首先列出3 个点与Ps点的距离关系，然后根据p1位置到p3位置的时间t13和p2位置到p3位置的时间t23与速度和角度的关系，用p3点的横坐标和纵坐标代替p1和p2点的横坐标和纵坐标，最终整理可得关于x，y 的方程组

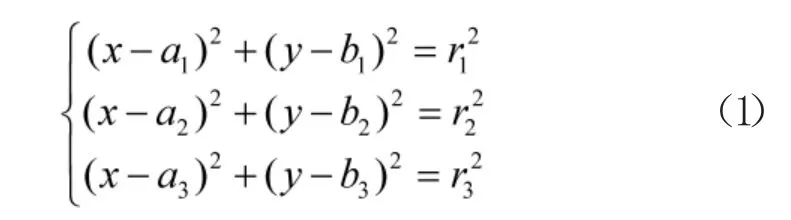
将式（1）写成矩阵形式，通过最小二乘法进行求解，由于求解过程中可能存在奇异的情况。引入改进的高斯距离迭代算法进行迭代求解，式（1）相当于坐标（x，y）与已知坐标的距离函数，令

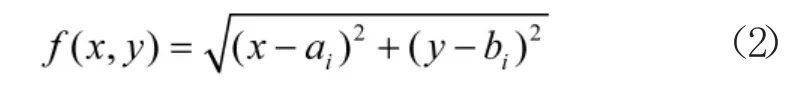
式中，i=1，2，3。

步骤3 为了减小速度和位置的误差，用泰勒级数展开进行线性化，首先设定AUV 的位置初始值和迭代阈值，其次用最小二乘法求出AUV 位置的修正量，将修正量与迭代阈值进行比较，若修正量小于迭代阈值，则停止迭代；否则采用信赖域的方法来更新步长，继续迭代。

首先确定一个位移长度（信赖域半径），并以当前迭代点为中心点，以此位移长度为半径确定一个闭球区域（信赖域）。然后求解这个区域内“信赖域子问题”的最优点，若此最优点能够使式（4）有足够的下降量，则接受此最优点为新的位移，同时需要保持或扩大信赖域半径继续迭代。否则，说明二次模型与目标函数的近似度没有达到目标，需要缩小信赖域半径，再通过求解新的信赖域子问题得到新的最优点作为新的位移。

循环执行步骤2、步骤3 进行新一轮的迭代计算，直到式（4）满足为止。

步骤4 取计算出的直线段的末端点作为下一直线段的起始点，继续进行下一直线段的迭代计算。

2 基于USBL 的组合导航建模

2.1 基于USBL 组合导航系统状态方程设计

将SINS 系统解算的速度、深度及到达距离差和斜距分别与DVL、深度计及USBL 系统的信息做差，作为滤波器的量测值进行滤波融合。综上所述设计出基于到达距离差和斜距的SINS/USBL/DVL/深度计组合导航子系统原理框图，如图3 所示［12］。

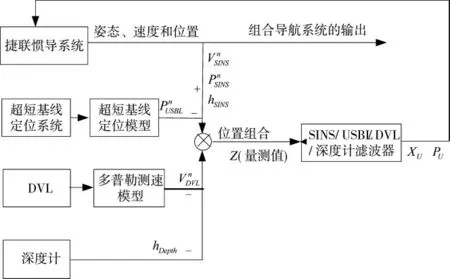
图3 SINS/USBL/DVL/深度计组合导航系统原理图

根据改进的基于斜距USBL 的误差模型，选取到达距离差和斜距误差作为状态量，USBL 系统状态变量为：

2.2 基于USBL 的组合导航系统量测方程设计

在基于USBL 的组合导航系统中，提高定位的精度以及实时性是最关键的问题，而在整个系统中，有以下几个亟待解决的问题：

1）在USBL 系统中，发射器端有一个由水听器组成的基阵，整个基阵尺寸较小，易在安装时发生偏移，则会对后续的导航定位产生较大的影响。

2）对于USBL 系统中纯距离定位法而言，计算过程中使用的最小二乘法会存在奇异值的情况，需要解决其中的奇异值，增强纯距离定位法的精确性。

3）对于SINS/USBL/DVL/深度计组合导航系统而言，将SINS 系统与各辅助系统进行融合，必须解决引入USBL 系统带来的滤波发散问题，以及历史信息对当前滤波值的影响，并保证滤波的实时性，使得滤波收敛。

3 基于USBL 的组合导航系统改进的自适应卡尔曼滤波算法设计

将SINS 系统与DVL、深度计及USBL 系统的信息做差，作为滤波器的量测值进行滤波融合，在滤波器内采用改进的自适应卡尔曼滤波算法进行滤波。基于USBL 的组合导航改进的AKF 算法设计如下：

1）状态预测

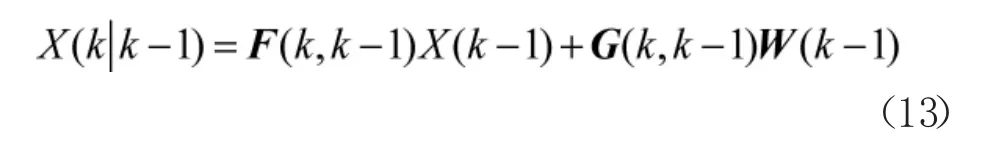
式中，X（k|k-1）为k 时刻系统预测状态向量，F（k|k-1）为k 时刻系统预测状态转移矩阵，X（k-1）为k-1时刻状态向量，G（k|k-1）为k 时刻系统噪声传播矩阵，W（k-1）为k-1 时刻噪声矩阵。

2）新息序列更新

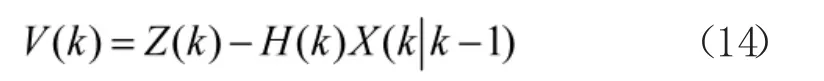
3）状态预测协方差更新

4）滤波增益矩阵更新

从式（16）和式（17）可以看出，滤波增益和系统状态估计协方差与测量噪声协方差R（k）相联系，R（k）对滤波的影响更大。所以对测量噪声协方差R（k）进行估算，从而减小计算量，提高实时性。

7）滤波的收敛性判据

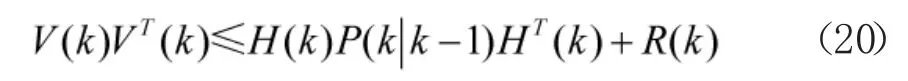
在滤波融合时，需要判断当前滤波是否收敛，若满足收敛条件，则R（k）=R（k-1）。否则，需要由式（18）估计新的R（k）值。

8）自适应渐消因子

式（23）中，β≥1 是为了使状态估计值更平滑引入的一个弱化因子。式中，ρ 为遗忘因子，V0为残差的协方差。

系统趋向平稳状态时，增益矩阵K（k）一般是接近极小值的，可预报残差V（k）则会在系统状态发生突变时增大，但从式（16）看出，增益矩阵K（k）不会随V（k）变化而发生相应的变化，此时滤波器无法对突变状态作跟踪处理。为了避免以上缺点，使滤波器具有强跟踪滤波的特性，以简化的Sage-Husa 自适应滤波算法作为基础模型，在线调整状态预测协方差和相应的增益阵。

强跟踪滤波器在线选择一个适当的滤波增益阵使：

相当于将不同时刻的残差序列作正交，其原理是为使得预报残差时刻具有类似于高斯白噪声的性质，在模型参数失配情况下，实时调整增益矩阵K（k）。

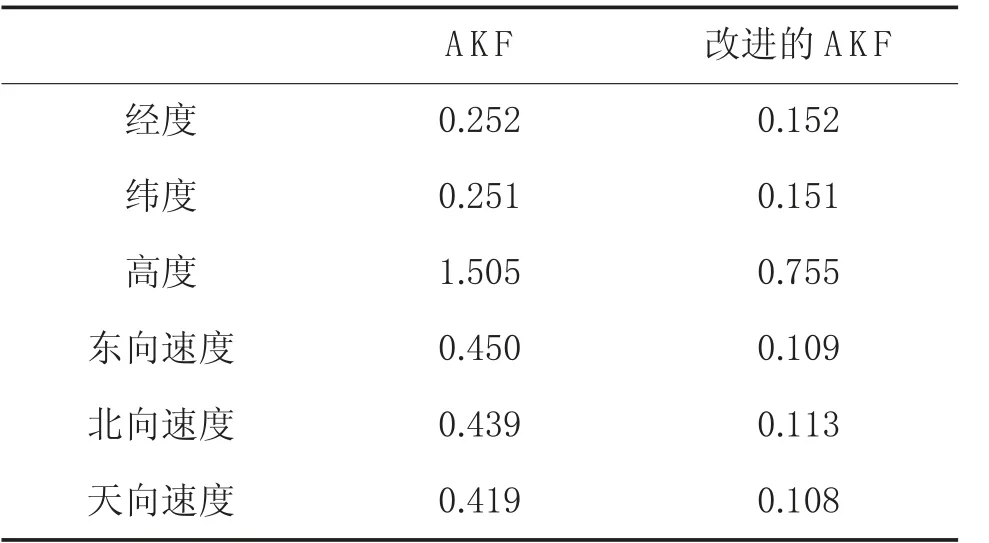
表1 状态估计各参数标准差

4 组合导航系统算法仿真验证

4.1 组合导航算法对比仿真

为了验证建立的基于USBL 系统辅助SINS 的SINS/USBL/DVL/深度计组合导航系统的误差模型和改进的自适应卡尔曼滤波算法下的性能，在MATLAB 下模拟环境进行仿真。在MATLAB 建立了SINS/USBL/DVL/深度计组合导航系统的模型，分别采用AKF 仿真和改进的AKF 算法仿真，并进行对比。

设置仿真参数条件：陀螺常值漂移为0.05°/h，随机偏移为0.05°/h；加速度计常值偏置：50 ug，随机误差为50 ug；DVL 精度为0.1 m/s；初始姿态角：纵摇为0°，横摇为0°，航向为30°；初始速度为1 m/s；初始姿态误差中纵摇误差为0.001 5°，横摇误差为0.001 5°，航向误差为0.001 5°；深度计误差为0.3 m；初始速度误差为0.018 m/s；初始位置误差中纬度误差为1.2 m，经度误差为1.2 m，高度误差为0.6 m；仿真结果如图4 所示，输出的变量主要有东北天向速度误差和经纬度、高度误差。

图4 组合导航两种滤波算法误差对比图

图4 为组合导航两种滤波算法误差对比图，其中，蓝色为组合导航在AKF 下的速度和位置误差，红色为组合导航在改进的AKF 下的速度和位置误差。表1 为两种算法下状态估计各参数的标准差，可以明显地看出，AKF 滤波作用下的导航系统东北天向速度误差及位置误差都得到了改善，其主要原因在于，提出的改进的自适应滤波算法，以简化的Sage-Husa 自适应滤波算法为框架，在滤波收敛性判据和强跟踪滤波思想双重作用下，改善了滤波收敛性和稳定性。

4.2 USBL 纯距离定位法辅助SINS 定位仿真

当AUV 行驶至USBL 作用的范围时，通过声学信号测量AUV 到配备有发射器的回收坞的斜距，再结合深度计测量的深度信息，通过改进的高斯距离迭代法进行定位，用得到的位置信息去修正SINS的位置信息，以改进的SINS/USBL/DVL/深度计组合导航方式导航定位。

仿真时间1 400 s，假设AUV 在500 s 后进入USBL 作用的范围，通过改进的高斯距离迭代法对SINS 导航进行辅助定位，分别对有无改进的高斯距离迭代法辅助SINS 定位进行对比仿真实验，用水平斜距误差率来衡量定位精度，即水平方向位置计算值与真实值之差，除以真实斜距值，水平误差率越小，其精度越高，其计算公式如下：

仿真结果如图5 所示。

图5 有无改进的高斯距离迭代辅助定位的水平斜距误差率对比

如图5 所示，整个仿真时间为1 400 s，设定AUV 在500 s之后进入USBL 作用范围，即500 s~1 400 s之间在改进的高斯距离迭代法辅助SINS 定位下，表2 则截取500 s后的5 个时刻，600 s、800 s、1 000 s、1 200 s及1 400 s时刻的水平斜距误差率进行对比，水平斜距误差率降低了90%左右，而且不产生发散，一直保持稳定。

5 结论

针对AUV 在对接回收中基于斜距的SINS/U S-BL/DVL/深度计组合导航的多传感器融合问题，研究表明，改进的高斯距离迭代法辅助SINS 的定位导航的变量参数更小，精度和稳定性更高，其主要原因在于，改进的高斯距离迭代法解决了计算中矩阵可能存在的奇异情况。且提出的改进的自适应卡尔曼滤波算法，能够在AUV 对接回收导航系统中起到较大的改进作用，使得AUV 的回收成功率变大。

表2 500 s后5 个时刻的水平误差率对比