寿命型产品序贯试验方案计算与分析

李大伟，姜本正，肖 冰

（解放军91550 部队，辽宁 大连 116023）

0 引言

可靠性是产品重要的质量属性［1］。为了检验产品是否满足可靠性指标要求，使其更好地完成规定的功能，需要开展可靠性验收试验。在制定试验方案时，序贯试验因为具有快速进行判决、减少平均试验时间等优点［2］，所以在工程中得到了广泛的应用，形成了多份相关标准［3-4］。

由于序贯试验方案的工程优点，自从20 世纪40 年代Wald 提出序贯概率比抽样检验方法以来，许多学者对序贯试验方案进行了大量的研究，比如文献［5］针对成败型产品，通过调整接收- 拒收判决线，在双方风险不变的情况下，降低了最大试验数；文献［6］在Bayes 理论框架下，推导了成败型产品的风险表达式，给出了判决准则。目前，相关研究［7-8］集中于对序贯试验方案判决准则进行改进，但是对于其判决概率基础模型研究相对较少。实际上，序贯试验方案采取“边试验边判决”的检验方式，造成存在多个判决时刻，导致其接收- 拒收判决概率模型、风险表达式等均较为繁琐，工程中往往采取近似的方法给出结果，不利于深入理解序贯试验方案的确定过程。为此，文献［9］以GJB899A-2009《可靠性鉴定和验收试验》规定的序贯试验方案8 为例，利用图解法给出了其接收概率处理过程，得到了精确计算结果。虽然结果与标准一致，但是作者并没有建立接收- 拒收概率模型的一般表达式，不利于进一步推广到其他序贯试验方案中。文献［10］虽然利用矩阵法给出了寿命型产品序贯试验方案的精确计算方法，但是缺少对模型概率意义的解释，且该方法对矩阵和概率知识要求较高，不利于直观理解序贯试验方案判决时刻的工程意义及确定内涵。由此可见，虽然序贯试验较为成熟，工程中为了便于使用，相关标准直接给出了可供查询的使用表格，但是其基础模型（即特征量解析表达式）研究相对较少。特别是序贯试验的概率计算较为繁琐，实际使用中主要利用近似或举例的方法，对相应的特征量计算过程进行了说明，需要进一步研究才能推广到一般情况。显然，这不利于准确理解序贯试验内涵，无法掌握序贯试验的物理意义和适用范围，给实际工作带来了一定的不利影响。

为了解决上述问题，本文以寿命型产品为研究对象，开展了序贯试验方案基础理论研究。利用概率方法，本文对序贯试验中接收和拒收对应的事件定义进行了分解、确定，建立了其接收- 拒收判决概率的基础模型，给出了双方风险、OC 曲线和平均试验时间等特征量的解析表达式，并进一步解释了序贯试验的物理意义。同时，通过与定时截尾试验方案进行比较，说明了序贯试验方案的工程特点，研究结论不仅有助于深入理解序贯试验方案内涵，而且能够掌握其适用范围，从而保证可靠性验收试验能够有序开展。

1 序贯试验方案概率建模

1.1 序贯试验方案描述

序贯试验方案采取“边试验边判决”的检验形式，因此，其试验方案往往采取表1 的形式给出。

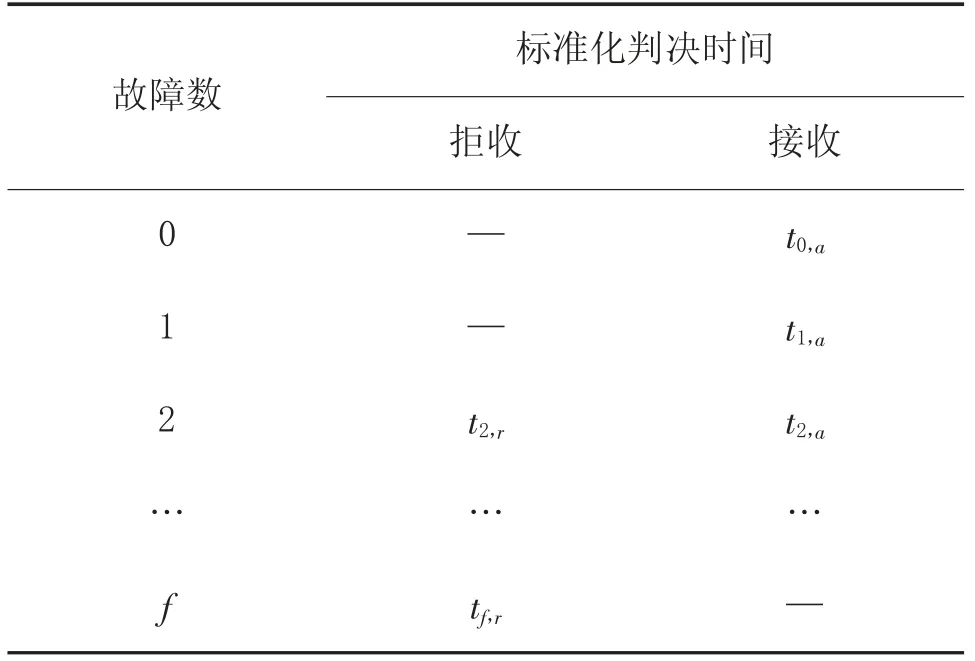
表1 序贯试验方案示意表

表1 中，ti，r表示产品发生第i 次故障的拒收时刻，即第i 次故障发生时刻小于ti，r时，则拒收该产品；ti，a表示产品发生第i 次故障的接收时刻，即第i次故障发生时刻大于ti，a时，则接收该产品。当第i次故障发生时刻在［ti，r，ti，a］之间时，则无法作出判决，需要继续进行试验。表1 中所列的判决时间为产品可靠性指标要求中最低可接受值θ1的倍数。

根据序贯试验方案的判决准则，每次发生故障都会参考判决时间，判断是否结束试验，因此，可以近似认为判决时间为试验结束时刻。此时，为了便于建立序贯试验方案的判决概率模型，本文按照判决时间的数值大小对表1 所示的序贯试验方案进行重新描述，具体如表2 所示。表中，判决时刻满足t1＜t2＜…＜tn。

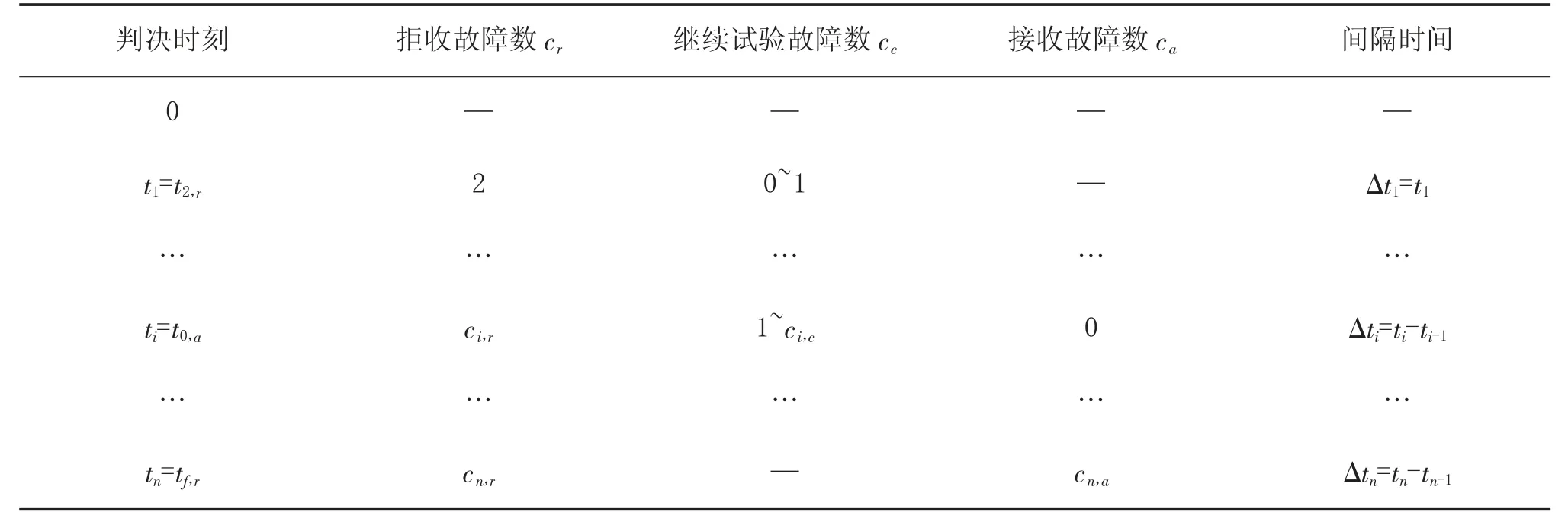
表2 序贯试验方案判决时刻示意表

表2 通过判决时刻，反映了产品可能结束试验的时刻。由于不同序贯试验方案在具体判决准则方面存在差异，因此，为了便于后文描述，对表2 作出以下说明：

1.2 接收- 拒收判决概率模型

对于寿命型产品，往往选取其寿命分布为指数分布，即产品的工作时间t 满足下式

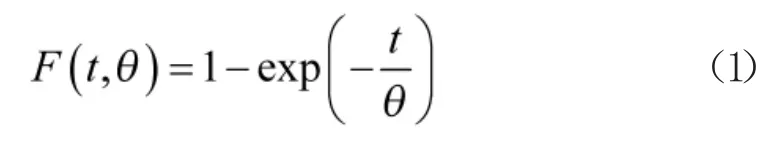
式中，θ 为产品的平均故障间隔时间（即可靠性真值）。为了分析试验方案的特性，通常θ 表示为产品可靠性指标要求中最低可接受值θ1的倍数。

根据指数分布与泊松分布的关系，寿命型产品在工作时间t 内发生k 次故障的规律满足下式

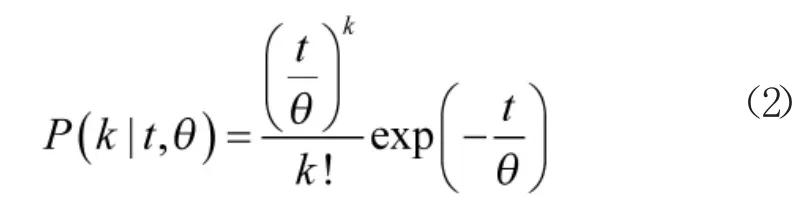
在掌握寿命型产品故障发生规律后，利用表2所描述的判决时刻，对序贯试验方案接收- 拒收概率进行建模。

1.2.1 接收概率模型

1.2.2 拒收概率模型

针对具体的序贯试验方案，根据判决时刻tj与拒收时刻ti，r之间的关系，利用式（6），能够得到产品的拒收概率满足下式

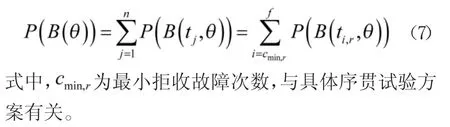
显然，序贯试验方案接收- 拒收概率基础模型的建立，有助于理解各个判决时刻对应的物理意义，并可推广到序贯试验方案的一般情况，为准确掌握序贯试验方案的特点和适用范围奠定了基础。

2 序贯试验方案特征量建模

2.1 双方风险

在掌握序贯试验方案接收- 拒收判决概率模型后，结合风险定义，给出生产方风险实际值α'和使用方风险实际值β'的解析表达式，即

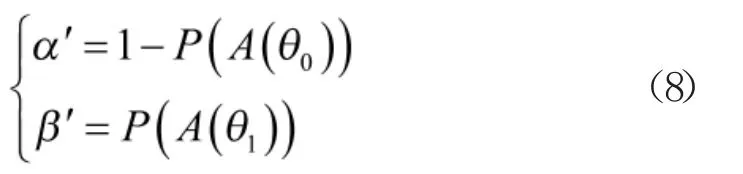
式中，θ0、θ1分别为可靠性指标中的规定值和最低可接受值。显然，双方风险与序贯试验方案的接收概率密切相关。

由于序贯试验方案采取“边试验边判决”的检验方式，因此，其双方风险为不同判决时刻接收概率的累加和，如式（8）所示。这说明：1）序贯试验方案是在给定双方风险的情况下，将风险逐步进行分解，以此确定判决时刻，并保证各判决时刻风险之和满足指标要求；2）序贯试验方案的风险与定时截尾试验方案的风险有所不同，由于后者判决时刻是唯一的，因此，定时截尾试验方案仅需要保证截尾时刻双方风险满足指标要求即可。从目标规划角度来看，可以近似理解为序贯试验方案的约束条件要多于定时截尾试验方案。

2.2 OC 曲线

OC 曲线反映了在给定序贯试验方案后，产品平均故障间隔时间的真值与接收概率的关系，利用接收概率（5），容易得到曲线满足下式

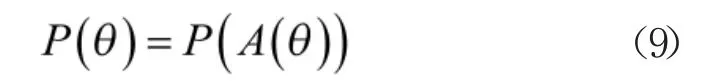
2.3 平均试验时间

对于序贯试验方案，试验结束有两种方式：接收和拒收。根据两种结束方式，分别获得平均试验时间。

2.3.1 产品接收时平均试验时间

根据序贯试验方案的判决准则，对产品作出接收判决只能在判决时刻，因此，利用式（4），能够得到产品接收时的平均试验时间ETTa满足下式

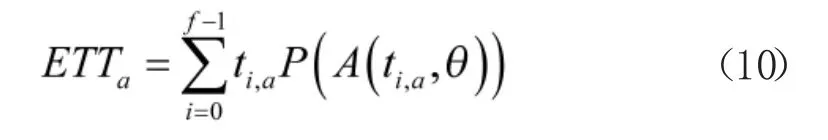
2.3.2 产品拒收时平均试验时间

由于产品故障发生的随机性，产品能够在任意时刻发生故障，当产品故障次数满足对应的拒收故障次数时，试验会因为拒收而结束，因此，利用式（6），能够得到产品拒收时的平均试验时间ETTr满足下式

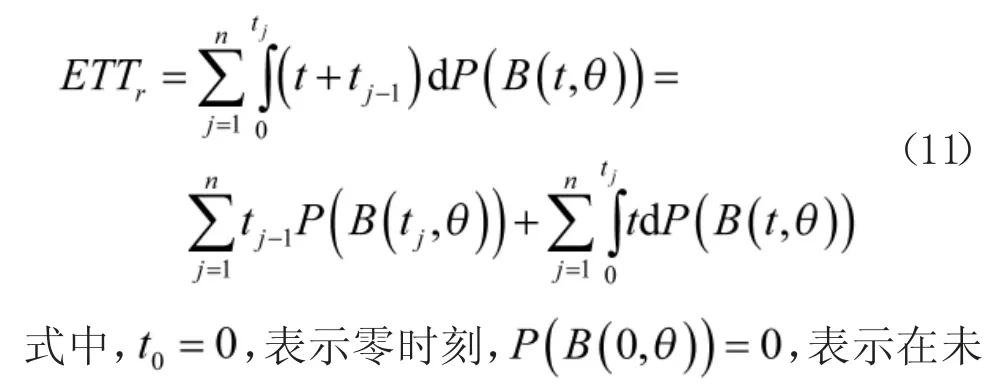
综上，得到序贯试验方案的平均试验时间满足下式

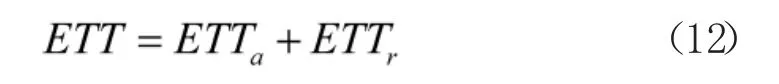
3 算例分析

本节以GJB899A-2009《可靠性鉴定和验收试验》规定的序贯试验方案6 为例，给出本文方法的处理过程和结果，以进一步说明方法的可行性。

序贯试验方案6 针对鉴别比d=3（即θ0=3θ1）和双方风险α=β=0.2 的产品进行考核，判决准则具体内容如表3 所示。

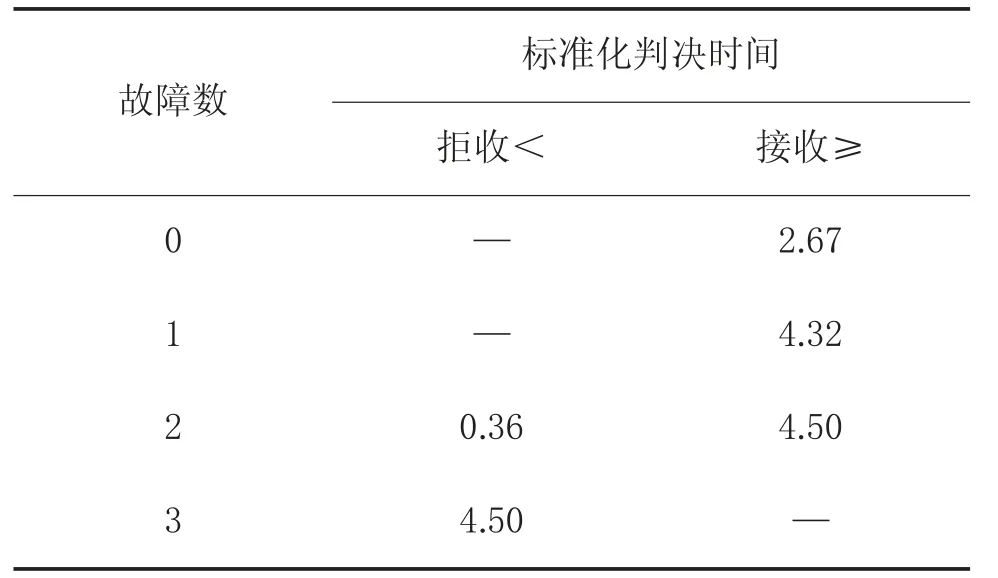
表3 方案6 接收-拒收判决标准

3.1 判决时刻表

利用表3，构造对应的判决时刻表，具体如表4所示。

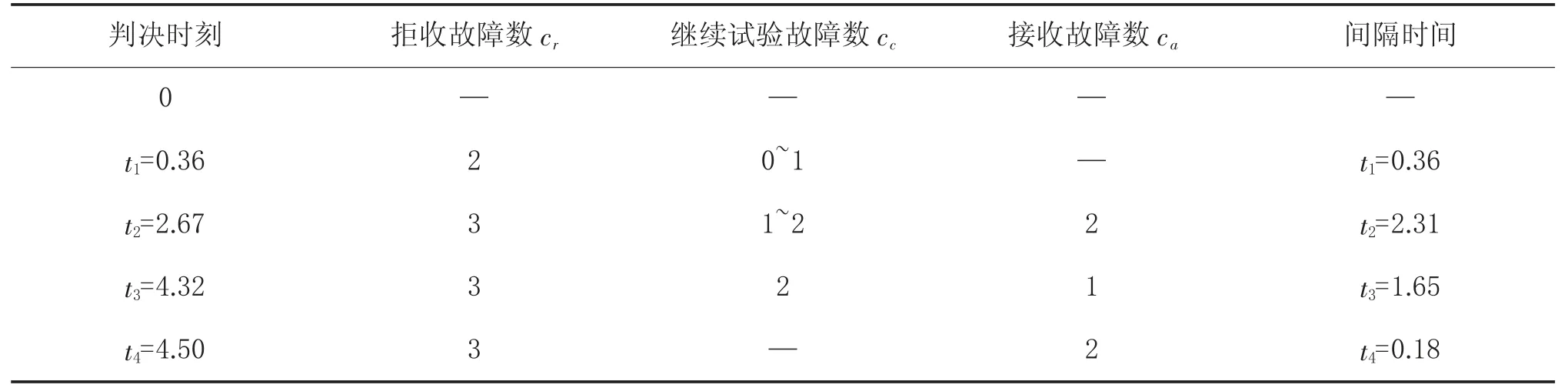
表4 方案6 判决时刻表

3.2 接收- 拒收概率

由表4 可知，接收时刻共有3 个，利用式（4），得到不同时刻接收概率为

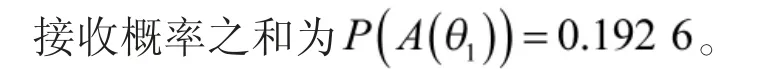
拒收时刻共有4 个，利用式（6），得到不同时刻拒收概率为

3.3 双方风险

利用式（8），能够得到方案6 所对应的双方风险实际值，具体为

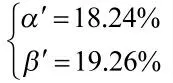
双方风险实际值与标准［4］给出的数值较为相近。

3.4 OC 曲线

利用式（9），能够得到产品平均故障间隔时间真值与接收概率之间的关系（即OC 曲线），具体如图1 所示。

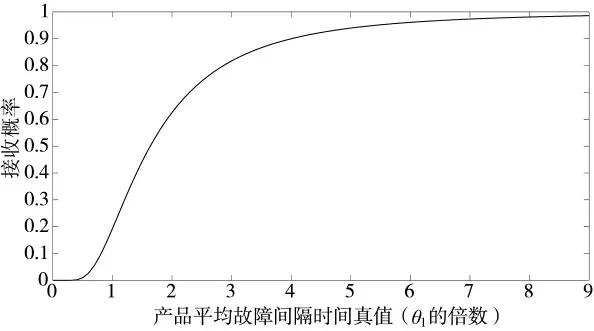
图1 方案6 的OC 曲线

该曲线与标准［4］给出的OC 曲线较为吻合，并反映了产品平均故障间隔时间真值越高，接收概率越大的规律。

3.5 平均试验时间

利用式（12），能够得到方案6 的平均试验时间，具体为ETT=2.581θ1。该值与文献［9］给出的数值较为相近，进一步说明方法的准确性。

3.6 与标准型定时截尾方案的比较

针对该产品，GJB899A-2009《可靠性鉴定和验收试验》规定的方案17（标准型定时截尾方案）同样可以进行考核。由于采取定时截尾，方案17 对应的平均试验时间为4.3θ1，显然，要高于方案6 的平均试验时间2.581θ1。这说明相比标准型定时截尾方案，序贯截尾试验方案具有作出判决需要平均试验时间较短的优点。

综上，本节通过对实际方案进行计算分析，验证了本文方法的准确性，并从理论上对序贯试验方案的工程优点进行了验证和解释，有利于工程人员对序贯试验方案的理解，使试验组织实施更加有序。

4 结论

本文对寿命型产品序贯试验方案基础模型进行了研究，取得了以下结论：1）建立了序贯试验方案不同判决时刻的接收- 拒收概率解析模型，并将其推广到一般情况，有助于准确掌握序贯试验方案的确定过程，为理解其内涵奠定了基础；2）给出了序贯试验方案特征量（双方风险、OC 曲线和平均试验时间）的解析表达式，为理解其特点和适用范围提供了理论支撑；3）通过算例分析，验证了本文模型的正确性，并与定时截尾方案进行对比，进一步说明了序贯试验方案的工程优点。