模数式桥梁伸缩装置疲劳试样尺度研究
吕彭民,孟庆贺,张维维
(1.道路技术与装备教育部重点实验室 长安大学,西安 710064;2.河北万亿交通设施有限公司,衡水 053400)
0 引言
桥梁伸缩装置是公路桥梁的重要附属构件,伸缩装置的安全性与耐久度对桥梁的正常通行有着重要的影响。由于伸缩装置所处的受力环境及受其结构的影响,伸缩装置容易发生破坏,从而影响到道路交通,伸缩装置的破坏形式主要有局部应力过大发生强度破坏、发生疲劳破坏、焊缝处开裂等几种情况[1~4]。对伸缩装置进行疲劳试验是验证装置疲劳性能的有效方式[5]。模数式桥梁伸缩装置规范试样尺寸不小于4m[6]。由于尺寸大,给室内疲劳试验带来一定困难。而现阶段国内外学者对模数式伸缩装置进行疲劳试验时很少定量考虑试样单跨试样与多跨试样对试验结果的影响。
本文首先采用力学简化模型,在相同加载情况下比较单跨与三跨模型的中梁应力、支反力的不同。其次以整体加强320型模数式桥梁伸缩装置为例,建立包含中梁、边梁、横梁、支座、橡胶、吊架等具体结构的精细化有限元模型,在相同加载情况下对比单跨与三跨模型伸缩装置危险点位置变化及危险程度情况,探讨用单跨代替三跨的可能性。最后对单跨模型进行承载力试验及疲劳试验。研究结果对模数式桥梁伸缩装置的疲劳试验提供一定的参考及借鉴。
1 伸缩装置简介及理论分析
1.1 整体加强型模数伸缩装置
本文选用的整体加强型桥梁伸缩装置结构简图如所示。其主要结构包括边梁、中梁、横梁、中梁支座、横梁支座、箱体、吊架等。
其中梁截面与普通模数式伸缩装置的王字型中梁截面不同,整体加强型伸缩装置的中梁较宽,并且增加一个止水带安装槽。整体加强型伸缩装置横梁承压与压紧支座采用球形座,中梁承压与压紧支座采用U型橡胶支座。采用伸缩铰链及弹簧来保证伸缩的均匀性。
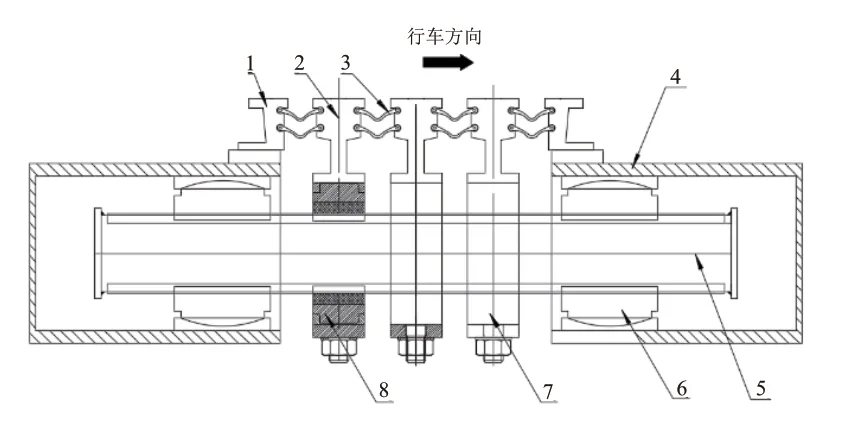
图1 整体加强320型模数式桥梁伸缩装置结构示意图
1.2 伸缩装置简化理论计算
按照规范要求[6],试样长度不低于4m,该伸缩装置中梁支座之间距离为1.25m,故疲劳试样至少要三跨以上长度,在采用三跨试样进行伸缩装置承载性能试验时,伸缩装置处在最大开口状态,加载位置在中间中梁中部,采用单轮加载,加载面积为200×600mm(如图2(a)所示),则只有中间中梁受载。由于中梁支座内含橡胶材料,为计算简便忽略中梁支座对中梁的弯矩约束,将均布力简化为加载在中梁中部的集中力,故中梁受力情况可以简化为图2(b)所示受力模型。

图2 三跨试样中梁受力简图
由材料力学可知,该受力模型为超静定结构,可采用叠加法对其进行求解,将图2(b)所示受力情况分为图3所示两种简单载荷的叠加作用。通过实际情况可知在第二中梁支座处挠度为零,构造变形协调方程为:

式中:P为将均布力简化后的集中力;EI为中梁抗弯刚度;l为伸缩装置一跨的跨距;FZ1、FZ2分别为中梁在第二、三中梁支座处所受的支反力。
又因为该受力模型为对称结构,则由式(1)可得:

三跨模型挠曲线方程为:

则三跨模型最大挠度在中梁中部为:

三跨模型弯矩方程为:
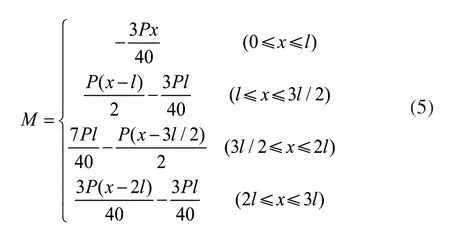
则三跨模型最大弯矩在中梁中部为:


图3 两种简单载荷受力简图
在采用单跨试样进行伸缩装置承载性能试验时,同理可将其简化为图4(b)所示受力模型。则由材料力学可知该模型支反力为FZ=P/2,单跨模型最大挠度在中梁中部为:

单跨模型最大弯矩在中梁中部为:

综上所述,由于中梁为横力弯曲且截面没有变化,故中梁最大弯矩之比即为正应力之比,则中梁应力单跨模型较三跨模型增加(M2-M1)/M1=42.8%;由支反力可知,中梁支座处支反力则减少了13%。
2 有限元模型的建立及计算
2.1 计算工况
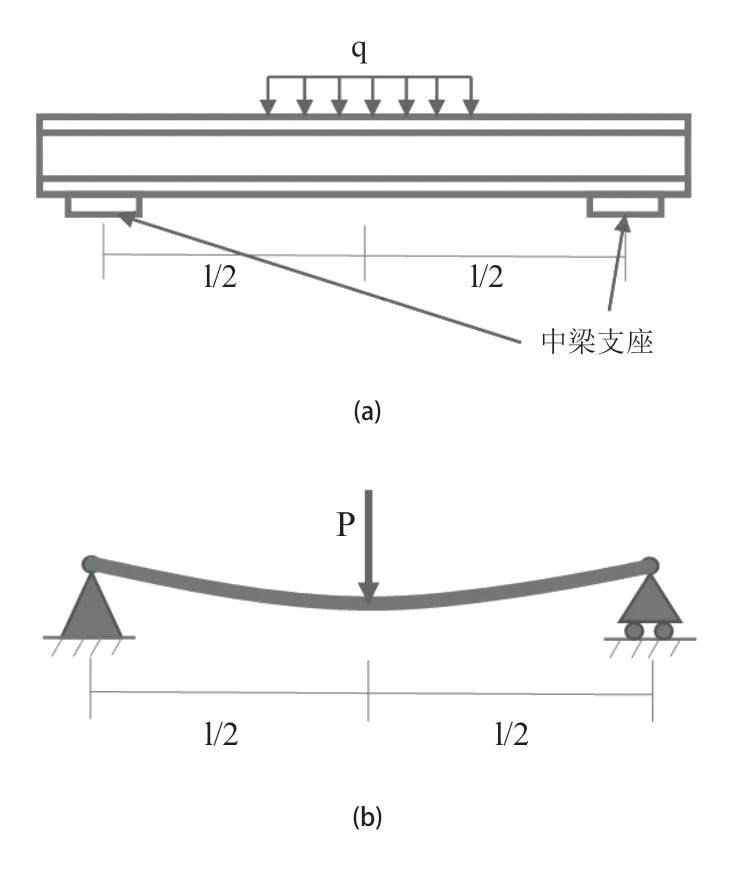
图4 单跨试样中梁受力简图

图5 三跨试样有限元模型
本文采用ANSYS有限元仿真分析方法进行结构静强度分析,取车辆轴重为200kN,根据行业标准JT/T 327-2016,确定载荷大小及冲击系数,即,在只考虑车辆对伸缩缝装置造成垂向作用的情况下,加载载荷为轮载100kN。
2.2 有限元模型的建立
根据整体加强320型模数式桥梁伸缩装置详细结构图纸,直接在有限元分析软件中建立单跨与三跨两套几何模型。为提高计算效率,省略在垂向加载情况下不起作用的铰链、锚固板及弹簧,并利用结构的对称性,采用对称边界条件,故只建立一半模型。所建伸缩装置模型处于100%开口状态,边梁与边梁间距为80×4+80×3=560mm。整个模型的材料均为线弹性材料(橡胶材料在较小变形时可视作线弹性材料),材料属性如下:
钢材的杨氏模量 E=2.06×105MPa,泊松比v=0.3,密度为 7850kg/m3;
橡胶垫的杨氏模量E=4000MPa,泊松比v=0.47,密度为 1300kg/m3;
横梁支座、球铰采用梁单元BEAM189模拟,此梁单元分别与箱体球面部分、球体支座剩余部分建立刚性区域,用以实现球铰建模,其余结构采用实体单元SOLID186模拟。三跨与单跨模型如图5、图6所示。
在中间中梁中部加载面载荷,在中梁、边梁中间截面上采用对称边界条件,位移箱采用全约束。
2.3 计算结果与分析对比
由图7可以看出三跨模型最大应力在第二中梁支座与中梁结合处为128MPa,中梁中间中部下表面为91MPa,由图8可以看出单跨模型最大应力在中梁中部下表面处为126MPa,其余构件如表1所示。

图6 单跨试样有限元模型

图7 三跨模型应力云图

图8 单跨模型应力云图
将三跨模型简化为单跨模型时,会使中梁中间部位下表面的最大应力增加,而中梁第二、三中梁支座处应力减小,这是由于将三跨模型简化为单跨模型后,中梁没有了第一、四中梁支座的约束作用,从而使中间受力部位的挠度会相对三跨时增大,应力相应增大,由表1可知中梁应力单跨模型较三跨模型增加38%,与1.2节中应力增加42.8%相近;由于少了第一、四中梁支座处向下的约束反力,则中间两个支撑点处的支反力就会减少,故中梁支座处应力减少。
在中梁支撑点处支反力减小的情况下,横梁和横梁支座处应力反而有所增大的原因是:由于中梁挠度增加,会使中梁作用在横梁上的附加扭矩增加,横梁在垂向支反力和附加扭矩的共同作用下,使横梁和横梁支座处合成应力有所增加(仅增加了几兆帕)。这些变化规律均符合力学原理。
经过查看两模型中中梁支座大应力部位的三向主应力得知,该部位大应力为压应力起主导作用,故在垂向加载情况下,单跨模型与三跨模型最危险点均为中间中梁中部下表面,且单跨模型中梁最大应力较三跨模型增大38%,故采用单跨模型进行疲劳试验时其结果偏于安全。
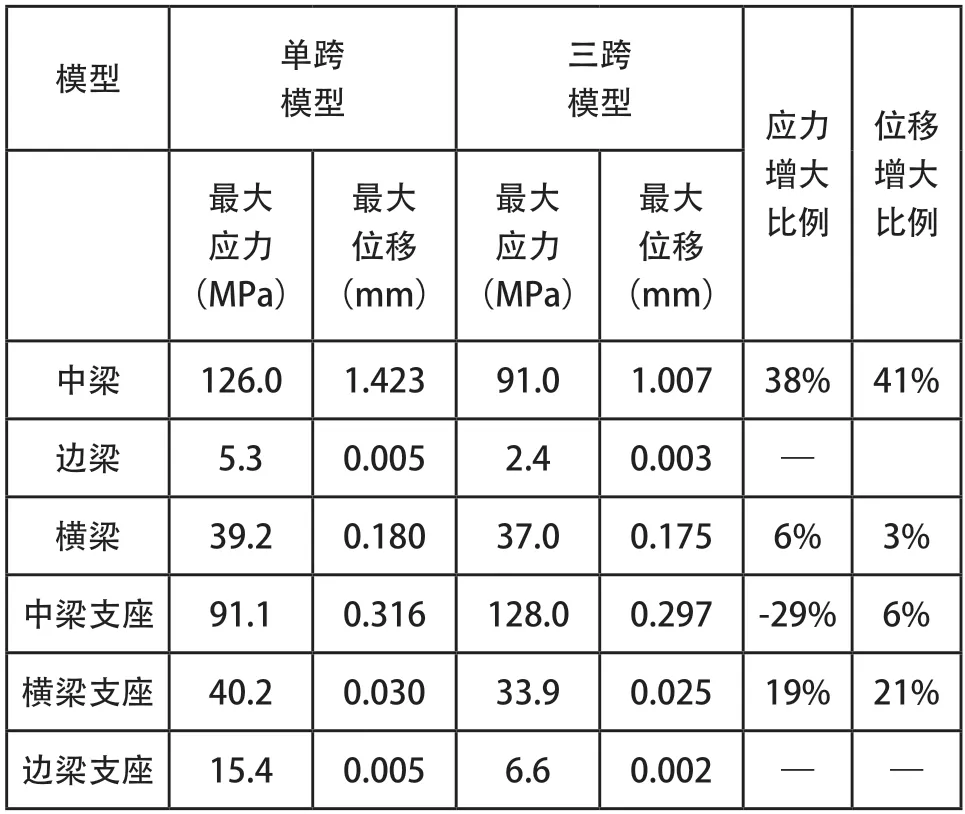
表1 单跨模型与三跨模型有限元分析结果对比
3 承载力试验及疲劳试验
3.1 试验方案
按照行业标准JT/T 327-2016,采用单跨试样进行静载试验及疲劳试验,为将试样与试验台连接,在试样四个位移箱底面焊接四个连接板,按行业标准中所规定的加载面积设计加载压头,在试样中间中梁中部下表面贴应变片。试验时:将试样在100%开口状态下固定在试验台上,并保证伸缩装置和试验工装在整个试验过程中不产生偏斜和滑移,压头下加装橡胶板模拟轮胎加载,实际试验整体装置如图9所示。承载力试验时:竖向载荷P=100kN,设计轮载的10%为步长,以1kN/s的速度加载,重复三次;疲劳试验时:竖向载荷P=55±45kN(Pmax=100kN,Pmin=10kN),加载循环200万次,加载频率为8Hz。

图9 伸缩装置疲劳试验主视图
3.2 试验结果
静载试验结果如表2所示。由表2可知,承载力试验时伸缩装置中间中梁中部下表面应力随着竖向载荷的增加而增加,整体呈线性趋势,最大应力为124.5MPa与表1中单跨模型有限元计算结果126MPa相当吻合,从而验证了本文所建模型的正确性。
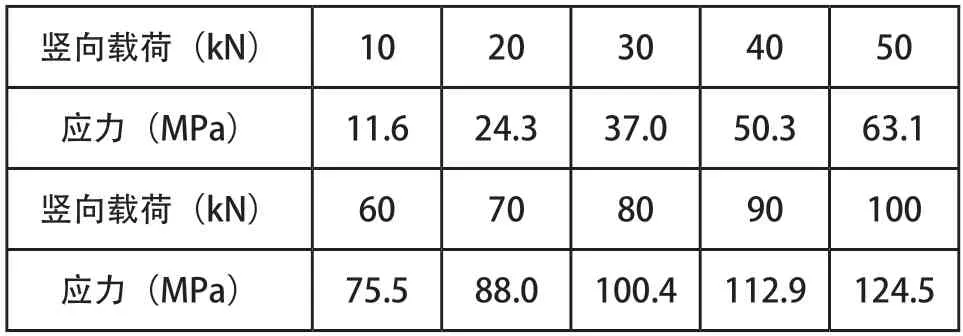
表2 承载力试验中间中梁中部下表面应力
伸缩装置整体在经过200万次疲劳试验后各零件细部的情况如图10所示,周围的紧固螺栓未出现松动滑脱现象,伸缩装置关键焊缝部位也没有出现裂纹,整体强度和性能完好,试验过程安全平稳无异常,振动噪声较小,满足设计要求。在100kN车轮载荷作用下,伸缩装置整体满足疲劳性能的要求。
4 结语
1)对单跨与三跨模型中梁受力情况进行简化后,分析可知中梁跨中应力单跨模型较三跨模型增加了42.8%,中梁支反力减小了13%;有限元模型结算结果为中梁跨中应力增加了38%,中梁支座应力减小了29%。两者所得规律一致。

图10 伸缩装置构造细节焊缝
2)由有限元分析可知,中梁中梁支座处最大应力主要以压应力为主,故采用单跨试样代替三跨试样进行疲劳试验,其结果偏于安全。即在试验条件受限时,可采用单跨试样进行疲劳试验。
3)通过伸缩装置承载力试验测得中梁应力,验证了所建有限元模型的正确性,通过疲劳试验验证了该型号伸缩装置疲劳性能满足规范要求。

