有限状态机在倍速链印花机控制系统中的应用
罗 勇,季诚昌,李培波,孙以泽
(东华大学 机械工程学院,上海 201620)
0 引言
传统的网版印花主要是人工印花,这种方式存在劳动强度大,工作效率低下等问题,因此各公司竞相研发自动化网版印刷机,本文主要针对学校研发的倍速链网版印花机的控制系统进行研究。
在倍速链网版印刷机的控制系统规划、设计与实现中,由于其自动化水平要求高,因此其控制流程的设计表达是一个很重要的环节,有效的设计表达不仅可以简化系统的复杂度、促进系统的快速实现、充分体现系统体系结构思想,而且可以通过这种形式主义的表达方式来验证控制流程的合理性,排除控制系统设计中的各种错误。
有限状态机(Finite State Machine,FSM)又称为有限自动机,是一种具有离散输入输出系统的数学模型,适用于多任务系统,可以清楚的刻画系统的现有状态及其状态的转换关系,清楚地模拟机器加工的工艺流程。
我们可以依据有限状态机理论对倍速链印刷机控制系统进行状态分析,设计倍速链网版印刷机的有限状态机转移模型,并由此设计出其控制流程,以实现机器运行自动化。
1 有限状态机
1.1 有限状态机原理
有限状态机作为一个描述离散型事件状态关系的抽象数学模型,它可以模拟世界上大多数事件的运行过程[1~3]。
有限状态机的四要素:状态(state)、转移(transition)、事件(events)、动作(action)[4,5]。状态指的是运行过程中所处的某一阶段;转移指的是从一个状态转移到另外一个状态的过程;动作指的是在状态转移时所做的操作;事件指的是触发状态转移过程的条件,可以来自内部也可以来自外部。有限状态机每时每刻都处于某个状态下,这个状态被称为当前状态或者源状态和现态,当前状态在转移条件的触发下,可完成一系列动作转移到下一个状态,这一状态被称为目标状态或者次态。
1.2 有限状态机的表达方式
通常,有限状态机的表达方式主要有三种,数学表达式、状态转移图和状态转移矩阵。下文将对以上三种方式进行分析。
其中:
1)S={S0,S1,S2,…,Sn}是状态机的状态集合,包含着有限个元素,每个元素都是其状态,系统在运行过程中处于某一确定的状态Si;
4)S0∈S表示的是初始状态,即机器开机时的状态;
状态机数学函数表达的方式可能不是那么的直观[6,7],所以通常我们会画出状态机的状态转移图,如图1所示的状态机其表达式为(S,,f,S0,Z)其状态集合为S={S0,S1,S2,S3}转移条件集合为={a,b}函数映射关系式为f(S0,a}=S1,f(S0,b}=S2,f(S1,b}=S2,f(S2,a}=S1,f(S2,b}=S3,f(S1,a}=S3,箭头的起点表示的是现态,箭头指向的是次态,一个没有起始的箭头指向初始状态,即S0,终止状态由双圆圈表示,即图中的S3。
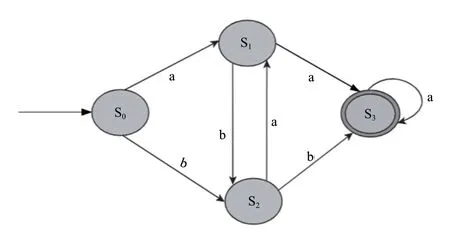
图1 状态机转移图
2 具体应用
2.1 状态机建立
倍速链网版印花机是一个多任务模型,在其运行过程中,需要同时完成定位、移载、印花、烘干等功能,因此我们可以将控制系统分为一个主系统和几个子系统,其中子系统有定位控制系统、移载控制系统、印花控制系统、烘干机控制系统,各子系统完成各自对应的功能。定位控制系统主要负责承印台的升降和承印板的定位夹紧功能,印花控制系统主要是负责印刷头部分刮刀、网版的运动和视觉对位平台的控制,移载控制系统主要负责倍速链的速度调节和一个移载功能,烘干机控制系统主要负责在完成印刷后对其进行一个烘干作用。主系统负责管理调用各子系统,如图2所示。
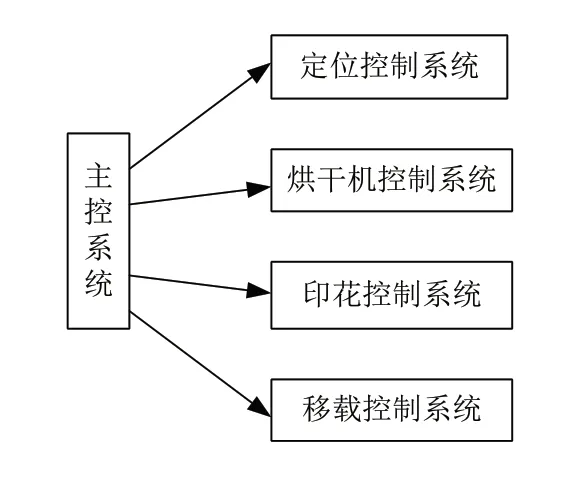
图2 主系统和子系统
一般来说在一个机器的运行过程中,每个动作的完成都不是瞬间完成的,是一个连续性的动作,也就说说其状态应该包括进行时和完成时。一个机器的状态通常主要包括:stopping停止中,stopped停止,aborting中止中,aborted中止,resetting重置中,idle空闲,starting启动中,execute执行,suspending暂停中,suspended暂停,unsuspending取消暂停中,holding持有中,held持有,unholding clearing解除清算,completing完成中,complete完成。在倍速链网版印花的状态划分中,我们主要有以下几个状态:idle空闲、starting启动、execute工作中,completing完成中、complete完成、reseting复位中、stopped暂停、stopping暂停中、clearing清除中、aborting中止中,abort中止。
在建立系统状态机时,我们可以在主系统和各子系统里面各建立一个状态机。我们的主控系统和子系统的状态机状态转移图相同,如图3所示。
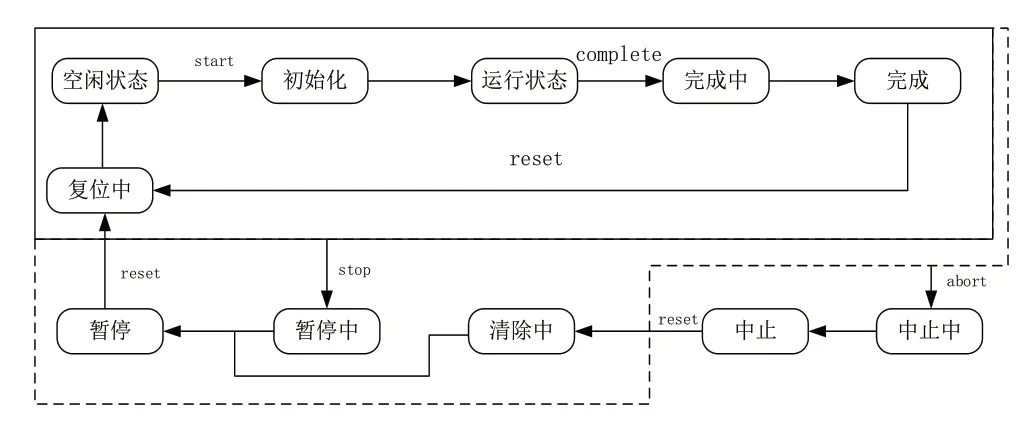
图3 状态转移图
由图3我们可以分析其主控系统的大致方案如下:在机器上电前,机器应该处于idle状态,即空闲状态,按下开机触摸屏上的开机按钮后,机器进行初始化;然后机器开始正常的印刷过程,印花完成后复位然后处于空闲状态;当机器运行过程中出现故障或者人为地发送abort指令后,它会往中止状态跳转,经历个中止中状态到达中止状态,机头上会有警报灯亮起,人处理完故障后可以通clear指令将故障信号清除,系统到达暂停状态,暂停状态下通过reset指令可以让其复位;当机器处于正常中运行中也可以根据需要人为地通过stop指令让机器暂停,机器从运行状态到暂停中状态,最后暂停动作完成,进入暂停状态,此时发布reset指令的话,机器会再次进行复位到达空闲状态。当机器处于idle、starting、execute、completing、complete、reseting可以接受stop指令;当机器处于idle、starting、execute、completing、complete、reseting、stopped、stopping、clearing状态时,机器可以接受abort指令。

子系统以主系统的进行时的状态作为自己的转移条件,即主系统在staring、stopping、reseting、completing、aborting、clearing等状态时,通过状态管理函数将使得子系统的状态也发生相应的转移,表现出一个主从关系。但是主系统里面的状态机主要是描述整个机器运行的一个状态,子系统里面的状态机则是通常要涉及到具体的工艺动作,比如在烘干机系统里面,故障停止的表现动作为,烘干机内部的温控器停止加热,但是烘干机内部的风扇继续运行;烘干机暂停时,温控器和风扇都会停止。
2.2 状态简化
前文提到的状态是我们按进行时和完成时划分的,我们将一个动作划分为完成时和进行时主要是考虑到一个时序关系,各部分工作能够协调完成。比如当我们的主系统收到一个start开始指令时,当主系统处于starting时,下面的子系统也开始相应的动作,如果等starting动作已经完成子系统才开始相应的动作,可能会造成一定的误差,整个系统的运行时间也会相应地增加。而进行时和完成时属于一个互斥关系,不会同时存在。
在我们的具体分析中我们可以根据正则表达式将其简化,将几个小状态看成一个大状态[8,9]。我们将reseting复位中与idle空闲看成一个大状态,我们将其命名为复位;starting开始中与execute运行看成一个状态,我们将其命名为运行;completing完成中和complete完成看成一个状态,我们将其命名为完成;将aborting停止中和aborted停止看成一个状态,我们将其命名为故障停止;将stopping暂停中和stopped暂停看成一个状态,我们将其命名为暂停。根据第三章中的简化理论,我们将状态机简化成图4所示。

图4 状态图
经过简化后的模型减少了进行中的状态,这使得我们后面的分析更为简单,有助于我们的理解分析。
3 仿真分析
下面我们对简化的状态机模型进行仿真分析。我们使用MATLAB软件里面的stateflow模块对其状态机进行仿真分析。Stateflow是MATLAB里专门用来对状态进行仿真的,主要是得到状态机的一个时序关系图。我们以数字量输入表示事件的输入,我们的指令事件有start指令,complete指令,reset指令,stop指令,abort指令,我们以数字量输入u=[1,2,3,4,5]依次表示上述的指令。我们的状态有5个,我们以数字量输出y=[0,1,2,3,4]依次表示复位、运行、完成、故障、暂停状态这5个状态。根据分析我们在MATLAB里面建立的有限状态机模型如图5所示。
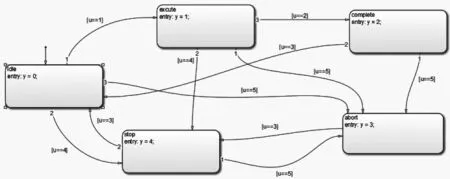
图5 模型图
接下来我们要建立整个状态机的输入输出模型,将整个状态机看成一个黑盒对其进行输入,如图6是我们的输入输出模型,在输入时我们simulink的In功能模块,其功能是能将外部数据导入为我们的输入,末端采用scope模块进行数据采样。我们将输入的数据设置为随时间变化的数组,可以按我们的需求对其进行输入,将其与我们的状态机模型的输入口u连接,输出y则是在0,1,2,3,4这5个数中变化的,将输出y与Scope的输入口连接,将我们的输出显示出来。
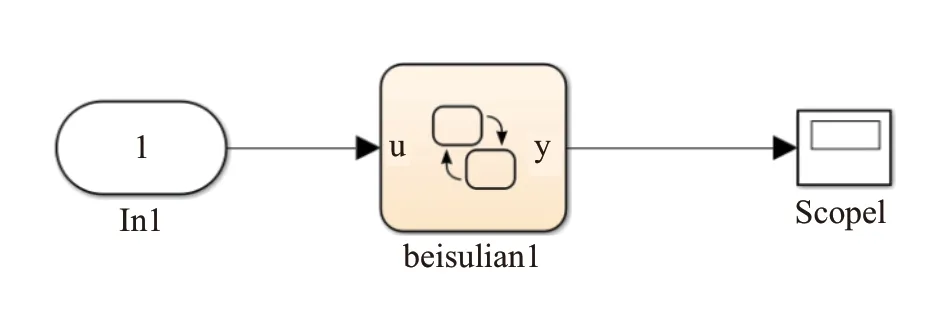
图6 仿真连接图
我们以u=[1 2 3 4 5 3 3]作为我们的输入,我们预期此状态机的功能是,第一步系统收到start指令到达运行状态;第二步收到complete指令到达完成状态;第三步收到reset指令,重新回到复位状态;第四步收到stop指令到达暂停状态;第五步,系统故障到达故障中止状态;第六步,收到reset指令,清除故障信号到达暂停状态;最后一步再次收到reset指令,回到复位状态。根据上面的分析我们得到的输出y=[0 1 2 0 4 5 4 0]。
如图7是我们的输入波形图,图3.4是我们的输出波形图,横坐标为时间,纵坐标为幅值。从我们得到的示波器波形图观察,我们可以得知u=[1 2 3 4 5 3 3],y=[0 1 2 0 4 5 4 0],我们发现结果与我们要求的一样。因此也可以证明此状态机模型应用在我们的倍速链印花机上
时可以实现我们的功能要求。
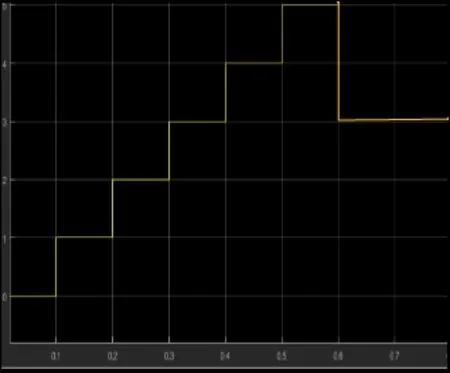
图7 输入波形
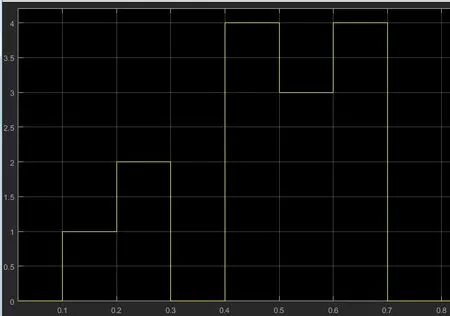
图8 输出波形
4 结语
为实现倍速链网版印花机的自动化过程,我们将有限状态机模型引入到其控制系统研究中,将机器的运行过程划分为几个状态。我们将状态机进行进一步简化,并通过stateflow建立起状态机模型后对其进行仿真,结果表明其状态机能够实现我们的要求。有限状态机思想的应用也使得控制系统更加简单明了,程序易懂,程序结清晰,有助于程序的调试和维护,自动化程度高,稳定性好,大大地提高了工作效率。

