基于相似日和RBF神经网络的短期电力负荷预测
王 瑞,孙忆枫,逯 静
(1.河南理工大学 电气工程与自动化学院,焦作 454000;2.河南理工大学 计算机科学与技术学院,焦作 454000)
0 引言
短期电力负荷预测主要目的是根据历史负荷和影响因素对未来的负荷情况进行预测,预测结果可以作为电力部门调度和分配的参考[1]。短期电力负荷预测中根据相似日数据进行预测可以利用较少的训练数据达到较高的预测精度,所以选择合适的相似日就尤为重要。文献[2]根据各类影响因素的动态加权和选取相似日;文献[3]运用虚拟相似日的概念,将一天多个负荷时段分别选取相似日;文献[4]通过构建相关因素特征矩阵智能识别相似日,并建立实时气象偏差校正策略对负荷曲线进行二次校正。以上方法都对相似日的选取有一定的意义,但都仅通过预测当天的负荷影响因素与历史日负荷影响因素做相关性分析来选取相似日,由于温度因素与其他影响因素不同,在持续高温的情况下,连续几日的温度变化对相似日选取也会有影响。本文考虑积温效应,将温度因素和其他影响因素分别进行相关性分析,最后通过计算综合相似度选取相似日,该方法考虑了积温效应对相似日选取的影响,使相似日选取更加准确。
RBF神经网络具有强大的非线性映射能力,是短期电力负荷预测中一种常用的方法[5],优化其隐含层参数设置可以提升模型整体性能。文献[6]运用交替梯度法交替训练RBF隐含层参数和输出层权值;文献[7]采用近邻传播算法来选取RBF的隐含层中心;文献[8]运用k-means聚类算法选择RBF隐含层参数。以上各种改进方法均提高了RBF模型的预测精度,但均是针对大量样本数据的RBF模型进行改进,并没有针对基于相似日数据的小样本RBF模型进行改进。所以本文采用改进的模糊c-means聚类对相似日样本进行处理,来确定RBF的隐含层参数,进而提升基于相似日的RBF模型预测精度。
1 改进的相似日选取方法
1.1 负荷影响因素分析
要建立短期电力负荷预测模型,首先要分析负荷与影响因素之间的关系[9]。气象因素与日期类型是电力负荷的主要影响因素,本文主要分析这两者对负荷的影响。这些负荷影响因素的量纲不同,所以在一起分析前需要将它们进行处理。
数值型影响因素用归一化公式进行处理:

其中,x'为归一化后的值,max(x)和min(x)分别为影响因素归一化前的最大值和最小值。
本文通过对待研究地区负荷变化进行分析,对非数值化影响因素量化值如表1所示。

表1 非数值影响因素量化值
1.2 综合相似度法
1.2.1 计算温度序列的动态相似度
在持续高温的情况下,前几日的温度变化也会对当天的负荷产生影响,所以即便当天与之前某日的影响因素类似,负荷情况也并不一定相同,考虑这种型精度的一种方法[10]。文献[11]通过对温积温效应,是提高负荷预测模度进行修正来考虑积温效应,本文直接在选取相似日时就将积温效应考虑在内。借鉴文献[12]中的思想并进行改进,在相似度公式中加入权重系数使之适应温度因素对负荷变化的影响,本文用改进的方法来计算温度变化的动态相似度。
用P0表示待测日及前k天的温度变化情况,
P0={X0,X1,…,Xi} i=0,1,…,k。P1表示历史日及前k天的温度变化情况,P1={Y0,Y1,…,Yi}i=0,1,…,k,本文k取2,即考虑连续3天的温度变化。X0和Xi分别表示待测日当天和待测日前i天的温度信息组成的序列,Xi=(xi(1),xi(2),…,xi(n))T,Y0和Yi分别表示选取的历史某日和该日前i天的温度信息序列,Yi=(yi(1),yi(2),…,yi(n))T。xi(k)和yi(j)分别表示待测日和历史日第j个温度信息的值,n为考虑的温度信息数目,本文n取3,考虑最高温度,最低温度和平均温度。对每个温度信息分别计算相似度:
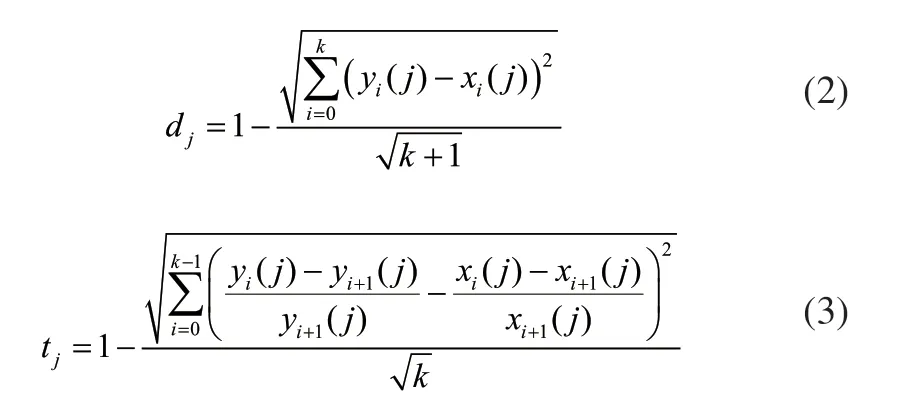
式中dj为第j个温度信息的数值相似度,tk为第j个温度信息的趋势相似度。因日期类型在其他影响因素中考虑,这里不再考虑。最后将n个温度信息结合起来可以计算出总体动态相似度:

式中ωj为第j个温度信息的权重,该权重由该温度信息与负荷的相关性得出。
1.2.2 计算其他负荷影响因素相似度
除去温度因素外,其他影响因素的变化趋势对负荷影响不大,所以将每日的影响因素放在一起计算相似度。x0和xi(i=1,…,N)分别为预测日和预测日前i天除温度外的其他影响因素构成的序列,除温度外的影响因素本文选择湿度,风速,天气状况,日期类型,xi=(xi(1),…,xi(m)),m为选取的其他因素个数,本文用灰色关联法计算其他影响因素的相似度。首先用下式计算x0与xi的灰色关联系数:

1.2.3 计算历史日综合相似度
本文用综合相似度作为相似日的评判标准。因温度的相似度与其他影响因素的相似度都对相似日选取有影响,但影响程度难以确定,所以本文采取文献[13]中因子相乘的方法来求取综合相似度。通过下式可以计算出历史日与预测日的综合相似度:

ηi为待测日前i天的综合相似度,综合相似度值越大,表明历史日与待测日负荷状况越接近,根据综合相似度排序选取相似日。
2 RBF神经网络模型
径向基函数(Radial Basis Function,RBF)神经网络因其能够逼近任意非线性函数的特点,近年来在预测领域取得了广泛应用[14]。它一般由输入层,隐含层,输出层三层组成。其隐含层激活函数为关于中心点径向对称衰减的径向基函数,所以具有局部逼近的特点,即输入信号只会激活少量神经元,使网络不容易陷入局部最优解。RBF神经网络结构如图1所示。

图1 RBF神经网络结构


式中ck为激活函数中心,σ为扩展常数。
网络的输出为:

3 改进RBF神经网络
RBF神经网络通常要确定三个参数:网络隐含层激活函数的中心,扩展常数和隐含层到输出层的连接权值。一般情况下,合理的隐含层参数选择往往能提高网络性能[15]。网络隐含层参数初值的选取一般由聚类来实现,本文通过待测日的相似日来挑选训练样本,样本数据差距并不大,所以选用模糊c-means聚类对样本进行聚类。模糊c-means聚类的初始中心的确定方法具有很大的随机性,一旦确定的中心偏差较大,将大大影响聚类效果。所以本文将样本先利用减聚类算法聚类,根据输出结果设置模糊c-means聚类的初始值再次聚类,这样可以很大程度上避免c-means聚类随机选取初值对聚类效果的影响。根据聚类结果设置RBF隐含层参数可以提高模型的性能。
3.1 隐含层激活函数中心确定
3.1.1 模糊c-means聚类
模糊c-means聚类是由Dunn[16]和Bezdek[17]提出的一种聚类算法,通过计算每个样本点的隶属度实现对样本数据的自动分类。它不是将样本归到一个特定的聚类,而是通过隶属度来表现其属于各聚类的程度,隶属度可以取[0,1]区间内的任何一个数。模糊c-means聚类原理如下[18]:
假设模糊c-means聚类要将数据样本集X={x1,x2,…,xn}划分成c类(2≤c≤n),V={v1,v2,…,vc},代表c个聚类中心,那么整个数据样本集的隶属度矩阵U可以表示为:

为了提高聚类效果,采用如下聚类准则:

式中:dik=||xk-vi||,为样本xk与聚类中心vi之间的距离;m为模糊加权指数,通常取m=2;J(U,V)为样本与所有聚类中心距离的二次方再加权求和的值。
通过求取J(U,V)的极小值,就可以得到模糊c-means聚类算法结果。
3.1.2 改进模糊c-means聚类
模糊c-means聚类的初始聚类参数对c-means聚类效果影响很大,所以需要其他算法进行优化。而减聚类算法可以有效反映出样本数据的分布情况,但得到的聚类中心是原数据中的点,不能反映聚类中心的真正含义,所以多数情况下被用来初始化一些对初值要求较高的算法[19]。所以本文用它来优化模糊c-means聚类算法的初值。具体步骤如下:
1)根据下式计算出所有数据样本的密度值[20]:
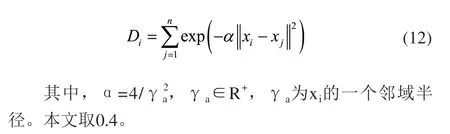
2)从中挑选出最大密度值为Dck,将其所对应的样本xc1设为第一个聚类中心,然后按照下式更新数据样本密度值:

3)从更新后的数据中再次挑选出最大密度值为Dc2,将其对应的样本xc2设置为第二个聚类中心,并用Dc2,xc2分别替换式(11)中的Dc1,xc1再次更新密度值,选择下一个聚类中心,当满足Dci≤εDc1(ε∈(0,1))时,停止运算,输出聚类中心,本文取ε=0.5。
4)根据输出的聚类中心设置类别数c和初始聚类中心V,模糊加权指数m,初始化隶属度矩阵U0,迭代步数l=0。
5)修正U

6)对于设定的ε>0,判断是否满足max{|ulikuikl-1|}<ε,如果满足,则跳到第(8)步,否则l=l+1,进行第7)步。
7)修正聚类中心V并返回第5)步。

8)输出聚类结果,并根据聚类结果设置RBF神经网络隐含层激活函数中心。
3.2 扩展常数确定
隐含层神经元的作用范围由扩展常数决定,扩展常数越大,作用范围越广,为了避免隐含层神经元作用范围太大或太小,隐含层扩展常数可以直接由下式求得:

式中l为隐含层中心数,cmax为隐含层中心之间的最大距离。
3.3 连接权值确定
隐含层到输出层的连接权值有很多方法可以得到,其中最小二乘法使用起来非常方便,快速,所以本文选用该方法确定连接权值,计算公式如下[21]:

式中xn为第n个输入样本,vc为第c个聚类中心。
4 基于相似日的RBF神经网络预测模型
本文结合相似日和改进的RBF神经网络模型进行短期电力负荷预测。具体步骤如下:首先将负荷影响因素量化和归一化,根据连续多日的温度变化计算历史日与待测日的温度动态相似度,然后再计算出其他影响因素的相似度,两者结合计算历史日综合相似度并据此选取相似日,并根据选取的相似日确定RBF神经网络的训练样本。在RBF神经网络隐含层参数初值的选取方面,运用模糊c-means聚类算法对相似日样本进行聚类,并用减聚类来优化模糊c-means聚类的初值,最后根据聚类结果设置RBF神经网络隐含层参数的初值并训练神经网络,用训练好的RBF神经网络来进行负荷预测。流程图如图2所示。

图2 基于相似日和RBF神经网络预测模型
5 算例分析
为了验证本文方法的有效性,在河南省某地区2018年96点负荷数据和气象数据中,选取3月~8月的数据作为样本,对连续高温的8月29日~8月31日进行96点负荷预测。
5.1 相似日选取
相似日选取的数量对负荷预测的影响也非常大,选取数量过少,模型训练不充分,预测精度较低,选取数量过多,训练速度慢,区别度较低。本文通过对8月高温日进行实验,得到了图3的结果,所以决定选取20日相似日作为实验的训练样本。

图3 相似日选择数量对预测误差的影响
同时由于本文综合相似度法中的温度序列动态相似度考虑的是连续3天的温度信息,所以在选取相似日时样本中前两日自动排除在外。作为对比,用灰色关联法在同样的样本中选取相似日。将两种方法选取的相似日负荷序列与待测日负荷序列各点方差的平均值进行比较,对比结果如表2所示。

表2 相似日负荷与预测日负荷的各点方差平均值对比
通过表2对比可以看到,对于连续高温日,综合相似度法选取的相似日效果更好,其选择的相似日负荷与待测日负荷各点方差的平均值更小,说明选出的相似日与待测日负荷更接近。传统灰色关联法选出的相似日负荷与待测日负荷之间的各点方差平均值比较大,说明该方法只能大致筛选出与待测日相似的历史日,但是筛选效果没有本文方法好。由此可见,本文改进的相似日选取方法与灰色关联法相比能够更加准确的选择高温日的相似日。
5.2 基于相似日的短期负荷预测
根据选出的20个相似日及其前几天的负荷数据选取RBF神经网络的训练样本。本文预测模型输入选择为X={x1,x2,x3,x1,x2},其中xa为待测时刻前a个时刻的负荷数据,a=1,2,3。xb为待测时刻前b天相同时刻的负荷数据,b=1,2。输出为待测点负荷数据。
5.2.1 实验评价标准
平均绝对百分误差(MAPE)可以用来评价模型的好坏,均方根误差(RMSE)对一组结果中极大或极小的误差反应敏感,也可以反映出预测精度。在同一预测模型中,MAPE和RMSE的值越小,预测结果越精确[22]。所以本文用MAPE和RMSE来评价各模型的预测精度,其表达式如下:


5.2.2 预测结果分析
用另外2种预测模型作为本文预测模型的对比,对8月29日~8月31日负荷进行预测。模型一:用灰色关联法选取相似日,模糊c-means聚类优化RBF隐含层参数;模型二:用综合相似度法选取相似日,模糊c-means聚类优化RBF隐含层参数;模型三:用综合相似度法选取相似日,减聚类与模糊c-means聚类结合优化RBF隐含层参数。预测结果如图4~图6所示。

图4 8月29日预测结果对比

图5 8月30日预测结果对比

图6 8月31日预测结果对比

表3 三种模型预测结果比较
通过图3~图5可以看到,连续三天的高温日,模型三得到的预测曲线与实际负荷曲线都更为接近,虽然模型一和模型二也均能预测出负荷曲线的变化趋势,但在一天的后半段预测误差较大,整体预测精度不如模型三。通过表3的预测误差对比可以清楚看到,对于预测的3天来说,模型二的MAPE和RMSE比模型一更小,说明用综合相似度法选取相似日比灰色关联度法效果更好。同时,模型三的MAPE和RMSE比模型二更小,说明本文用减聚类优化c-means聚类的初值可以获得更优的RBF隐含层参数,从而使预测精度更高。由此可见,本文提出的相似日选取方法和改进的RBF神经网络算法可以提高短期负荷预测精度。
6 结语
本文通过考虑积温效应,将温度影响因素与其他负荷影响因素分开计算相似度,再根据综合相似度选取相似日,在减少输入样本数目的同时,也提高了样本质量。在RBF神经网络预测模型中,根据本文训练样本特征和模糊c-means聚类在初值选取方面的不足,利用减聚类来优化模糊c-means聚类的初值,运用模糊c-means聚类选取网络的隐含层参数,提高了RBF预测模型的精度。最后根据实际负荷数据对河南某地区连续高温日进行预测,结果表明本文方法可以提高短期负荷预测精度。

