基于PSO算法的工业机器人绝对距离自标定方法
陈 爽,张 桥
(江西理工大学 机电工程学院,赣州 341000)
0 引言
工业机器人是一种具有很高的重复精度的多关节机械臂,通常采用D-H法来计算机器人末端位姿。机器人厂家一般以设计参数作为机器人的D-H参数,造成机器人末端位姿存在偏差。对机器人进行标定是提高精度最实用的方法,通常包括建模、测量、识别和补偿四个步骤[1~3]。
国内外众多学者对机器人的标定方法开展了相关研究工作,最直接的方式值采用高精度测量仪来标定,如任永杰等人[4]采用轴线测量法测量出各关节轴线扭转角后,再使用激光跟踪仪对D-H参数中其它误差进行标定使IRB2400机器人定位误差平均值从0.8776降低到0.1878。杜亮等人[5]利用激光跟踪仪对机器人末端位姿进行测量,再通过剔除D-H法中不可辨识的参数建立误差模型,对机器人进行辨识和补偿,使机器人定位误差平均值从2.5350降低到0.3582。戚祯祥等人[6]提出了基于机器人位置矢量误差模型的标定方法,使用激光跟踪仪跟踪机器人末端,利用广义矩阵计算出机器人末端误差向量的最小二乘解,对六关节工业机器人进行了标定,使机器人定位误差平均值从1.1677降低到0.2509。这种类型的标定方法需要较为昂贵的标定设备以及熟练的操作人员;近年来,由于光学测量技术的发展,立体视觉标定[7,8]方法也正在兴起。采用视觉系统进行标定在原理上和前者基本一致但相对于前者来说降低了大量成本。为了降低标定成本以及操作难度,许多学者开始研究机器人的自标定算法。张铁等人[9]利用修正D-H模型,推导出基于空间两点间的距离误差模型,经过标定后,机器人精度提高两倍以上。胥素芳等人[10]通过对机器人控制模型和误差模型进行独立建模,采用空间绝对距离对机器人进行自标定,使机器人绝对精度提高了十几倍。Ahmed Joubair等人[11]通过机器人探测靶球的球面来拟合靶球球心,再以拟合的三个靶球绝对距离误差的最小二乘解来标定机器人参数误差。
本文以六自由度焊接机器人为研究对象,设计了一个如图1所示的标定平台,标定锥固定在标定板上,两个标定锥顶尖之间的距离是固定的,并且能够精确测量。标定板可以绕球铰中心进行旋转,使标定锥达到不同的位置并夹紧。从机器人的设计参数出发,建立D-H模型,通过机器人末端执行器去探测该标定平台上的两个标定点之间的距离,通过探测点之间的理论关节角与实际关节角之间的映射来建立参数误差模型,参数除关节角之外的D-H参数进行识别,再对其进行补偿,使模型中的参数更接近于实际参数,进而提高机器人的定位精度。
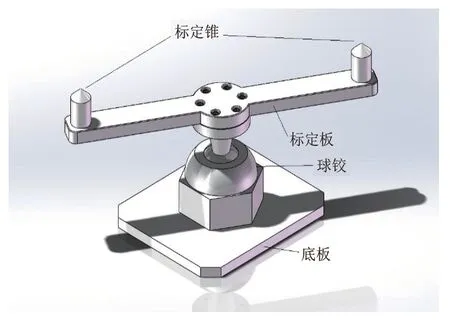
图1 标定平台
2 误差模型的建立
为了保证工业机器人控制算法的稳定性以及快速性,各工业机器人厂家生产的控制器中预制的机器人模型均采用D-H模型。本文依旧采用D-H法对工业机器人进行建模分析。
D-H法规定,机器人相邻关节的坐标变换由连杆转角αi、连杆长度ai、连杆偏距di以及关节角θi表示。从关节i-1到关节i之间的坐标变换为:

对应矩阵形式为:
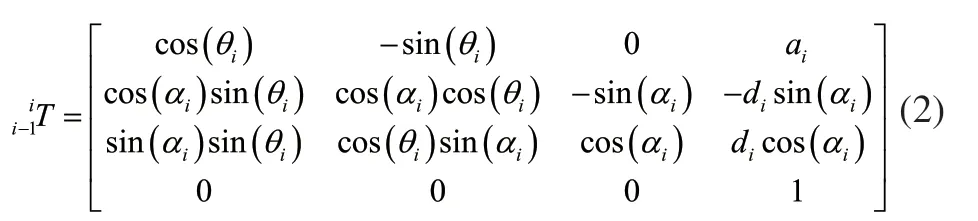
机器人末端工具位姿便可由此计算得出:

由D-H法确定的机器人连杆间参数误差矩阵为:

由于机器人减速器存在背隙,皮带等存在变形以及齿轮传动存在齿隙等,各关节的双向回零精度存在较大误差,采用智能算法进行迭代标定不仅极大增加了标定计算量,而且优化过程处于震荡的不稳定过程[12],并且各机器人生产厂家会在机器人各关节角零点设置零点标志,包括对零点开标定槽以及设计零点标定装置[13,14],采用硬接触等方式精确标定关节角零点,本文以已经标定过零点的机器人为研究对象,故在此不再对关节角零点进行标定,将标定空间从24维减少至18维,于是有:

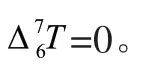
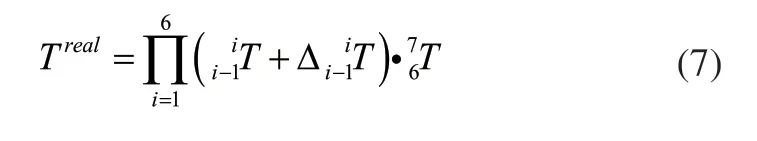
将式(7)展开并略去高阶项,得

以向量p表示点在基坐标系中的位置,向量形式表示为p=[x,y,z]T,则空间点m、n之间的距离可以表示为:
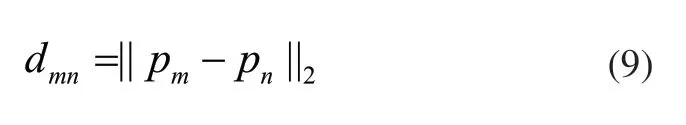
机器人的位姿矩阵T中第四列第一至三行分别表示末端的x、y、z坐标值,所以机器人末端探测的两点间的距离误差为:
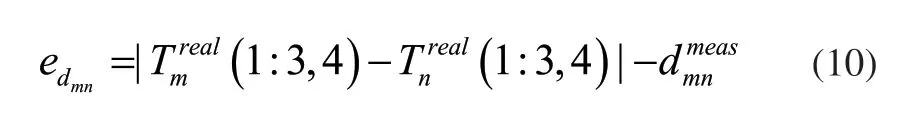
在理想情况下,人工操作机器人探测的点m,n之间的距离应与其理论距离相等,即edmn=0,但由于机器人模型误差、扭转角误差以及受力变形等各项误差未予考虑,造成edmn≠0。因此,本文采用PSO算法对该模型进行寻优。

表1 艾利特EI66-A140的设计D-H参数
本文以艾利特EI66-A140焊接机器人为研究对象,该机器人D-H参数以及各关节坐标系分别如表1以及图2所示。
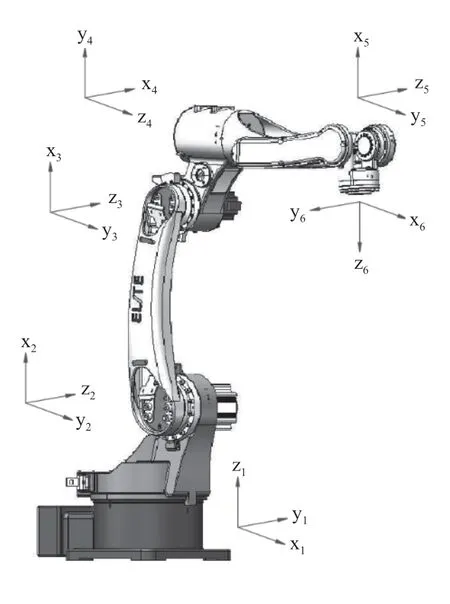
图2 艾利特EI66-A140关节坐标系
由于末端执行器的结构是自行设计的,其形位公差都能够直接保证,即式(4)已知。并且,为了达到操作简便以及摆脱高精度测量仪的束缚,标定过程未对机器人姿态进行考虑。本文中,只采用位置误差对机器人18个D-H参数进行标定。
考虑误差的D-H参数如表3所示。

表3 考虑误差的D-H参数
3 参数辨识
标定过程中,两个标定锥顶尖刚性固定在标定板上,标定板通过球铰与工作台连接,改变板的方向,两个标定锥的空间位置发生改变,但两个标定锥的距离不变。
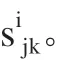
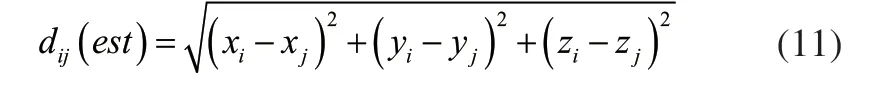
探测误差为:
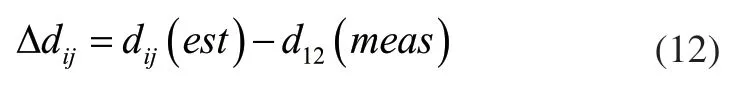
其中,d12(meas)为两标定锥顶尖之间的测量距离。
4 PSO算法误差辨识
PSO(Particle Swarm Optimization)算法是Kennedy,J.和Eberhart,R等根据鸟类捕食行为中通过群体中个体之间的协作和信息共享来寻找最优解的远离开发的智能算法[15]。PSO算法优化模型中的参数大多已预制,需要用户调节的参数较少,优化过程易于实现。除此之外,PSO算法不要求优化函数的连续性以及其他性质,适用性极广,对多变量、高度非线性、不连续及不可微的情况更加具有其优势,本文将其应用于六关节机器人参数识别过程。
利用PSO迭代算法对表3中所示的18个参数的误差值进行计算,使式(12)中探测误差最小。每次迭代时更新向量Δdij,当连续两次迭代之间达到所需的阈值均方根误差(RMS)时停止该过程,c使机器人的D-H参数从设计值向实际值逼近,步骤如下:
4.1 粒子群赋初值
根据D-H法可知,六关节机器人共有24个参数,本文对除关节角之外的18个参数进行标定,粒子群算法的搜索空间有18维,以实际参数与设计参数的偏差作为标定对象,记为:
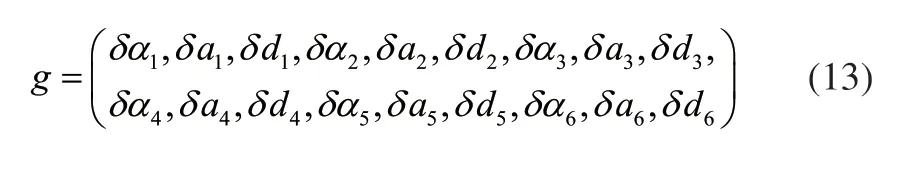
4.2 适应度函数
在粒子群进行搜索的过程中,需要对搜索方向进行判别,即采用适应度函数来表征搜索方向的优劣性,以机器人探测的两点间距离误差的倒数作为本算法的适应度函数。
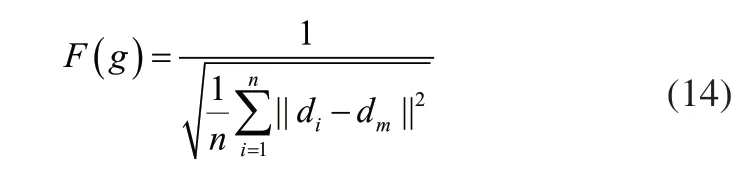
式中,di为标定平台为i方向时机器人探测后拟合的两个标定锥之间的距离,dm为两个标定锥顶尖的测量距离。
4.3 粒子群位置更新
在搜索过程中,粒子会不断迁移,每次迁移之间的迁移可以用粒子速度来表示:
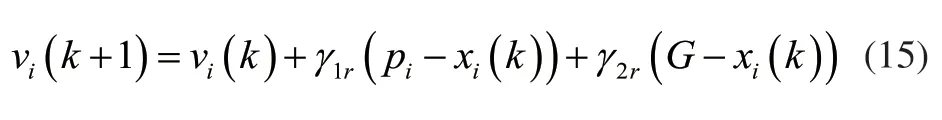
式中,vi(k+1)为粒子i在第k+1次迁移时的速度;pi为粒子i的局部最优值,G为粒子i的全局最优值;xi(k)为粒子i在第k次迁移的位置;γ1r和γ2r分别为控制局部最优和全局最优速度因子。
第i次迭代时,粒子群位置为:
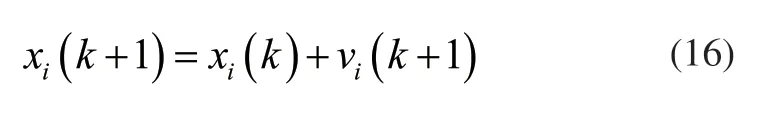
4.4 粒子群迁移终止条件
当粒子群达到预设的迁移次数或者相邻迭代目标函数达到设定值终止迭代,并输出最优位置以及最优目标值。
5 仿真与实验
通过图3所示艾利特EI66-A140机器人末端锥尖探测标定平台锥尖,并记录每组关节角,再使用PSO算法对其进行辨识,设定种群数量为50,迁移最大速度为10%,收敛精度为1e-5,最大迭代次数为2000次,MATLAB进行误差参数辨识过程如图4所示,经过150次左右迭代后,目标值不再减小,程序输出最优解。

图3 自标定现场
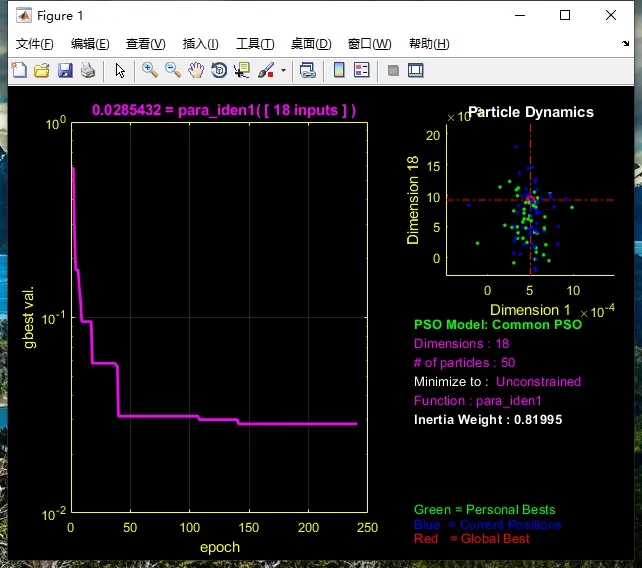
图4 PSO误差参数辨识图
D-H参数误差辨识结果如表3所示。
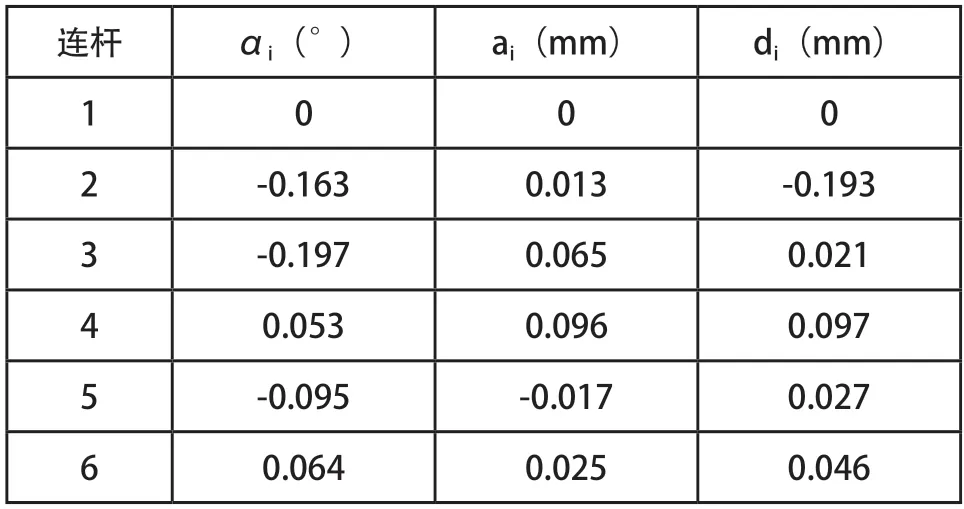
表3 D-H误差参数表
对机器人D-H参数进行补偿后,将靶镜安装在机器人末端,再使用激光跟踪仪分别对机器人运动范围内20个随机点位置精度进行评估,测量过程如图5所示,结果如表4所示。

图5 测量现场

表4 误差分析
标定前后绝对位置偏差如图5所示。
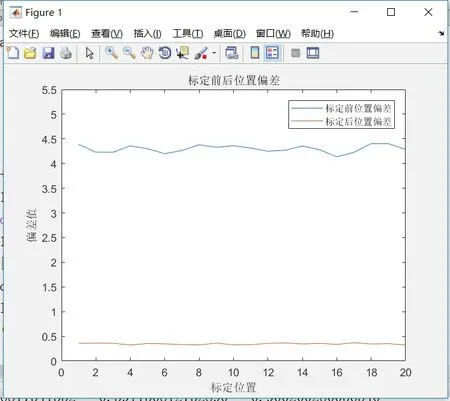
图5 标定前后位置偏差图
通过表4、图5可以看出,采用PSO算法迭代标定后的机器人末端位置精度显著提高。标定后位置精度提高了10倍以上,均方根误差相较于标定前有数量级上的提升,说明机器人标定后,各项误差与机器人实际误差高度一致,从而保障了机器人工作过程的精确性。
6 结语
本文提出了一种提高多关节串联机器人绝对精度的标定方法,该方法测量过程简单,并且不需要依赖高精度测量设备,有利于生产现场以及长时间运行的机器人校准的普及化。本文从D-H参数法出发,推导出了D-H误差参数与机器人末端误差的映射关系,再转化为D-H误差参数与空间中两点间绝对距离的映射关系,最后采用PSO算法对该标定模型进行寻优。
实验证明,相较于传统标定方法,本文所述方法具有计算量小,收敛速度快等特点,并且不依赖于高精度测量设备。误差补偿后机器人末端绝对误差均值以及方差均大幅降低,能够满足机器人实际使用要求。

