轨道交通延误条件下列车跳站与客流控制协同优化模型

杨陶源，赵鹏，姚向明，张璞

(北京交通大学，交通运输学院，北京100044)

0 引言

城市轨道交通延误事件给乘客出行带来诸多不便，如何科学合理地制定突发事件下的运输组织方案，对城轨系统的运营安全和乘客出行的高效稳定有着重要现实意义。轨道交通延误事件根据故障持续时间可分为扰动(Disturbance)、延误(Delay)、中断(Disruption)[1]。扰动发生频率高，持续时间多为3 min以内，具体表现为单列车延误，不影响后续车次，仅通过调整列车运行及停站时间即可恢复正常。延误发生频率低，持续时间为3～15 min，具体表现为延误发生后波及后续多列车次，仅通过压缩区间运行及停站时间已无法恢复正常行车秩序，此时需通过跳站停车、取消部分车次等措施进行调整。中断发生频率极低，持续时间一般为15 min以上，运输企业通常采用中断故障区间行车并封闭车站的措施。由于延误事件对行车秩序的影响较大且调整措施复杂，处理不当可能演变为中断事件，故本文仅针对延误事件进行研究。

跳站停车模式可以有效利用延误造成的运行图空间，是延误事件下调度调整的有力手段。针对城轨列车跳站停车模式，Altazin[2]兼顾了运输企业和乘客效益，但未考虑列车容量。面对我国城轨系统满载率较高的现状，Gao[3]以乘客延误时间最小为目标，在考虑列车容量约束的基础上，采取跳站停车措施恢复延误下的列车秩序；Shang[4]在跳站停车模式中考虑乘客公平性，使各车站乘客候车时间更为均衡。在突发延误条件下，大量乘客滞留会带来安全隐患，故列车调整与客流控制协同优化十分必要。Li[5]通过进站客流量和列车到发时刻的协同控制实现对列车运行扰动的恢复。然而，面对较长时间的延误，仅通过调整列车到发时刻已无法恢复正常行车秩序，如何采取有力的调度及客流协同管控措施对保障运营的稳定性具有重要意义。

综上，本文面向我国城市轨道交通突发延误场景，统筹考虑行车秩序的恢复和乘客集散的公平、效率，以跳站停车和多车站进站客流量协同控制为手段，构建双层线性规划模型优化城轨突发延误后的运输组织，并通过实例验证方法的有效性。

1 问题分析

对于大运量的城市轨道交通系统，突发延误事件不仅会造成列车延误，还会导致大量乘客积压滞留。列车延误下的运输组织，客流管控措施的制定需要依赖于调整后的行车组织方案，而客流管控措施反过来又会影响行车组织方案。因此，行车组织方案和客流管控措施是相互耦合的，突发事件下的运输组织工作必须统筹考虑行车秩序恢复和客流疏解。

1.1 延误下的列车调整问题

当城市轨道交通线路上发生延误事件时，调度员为保证行车安全通常对后续列车采取车站扣车措施。如图1(a)所示，D 车站8:14-8:18 发生信号故障导致02 次列车延误，后续的03 次列车在C 站停车等候调度命令。故障恢复后由于仅靠压缩追踪间隔和停站时间已无法恢复正常行车，导致06 次列车被取消并影响后续列车接续。如果采取图1(b)所示的跳站停车方案，02～06 次列车在部分车站通过不停车，则可以充分利用故障造成的运行图空间尽快恢复行车秩序。可见，相较于常态运营场景，在延误场景下采取跳站停车的调度措施更具可行性和必要性。

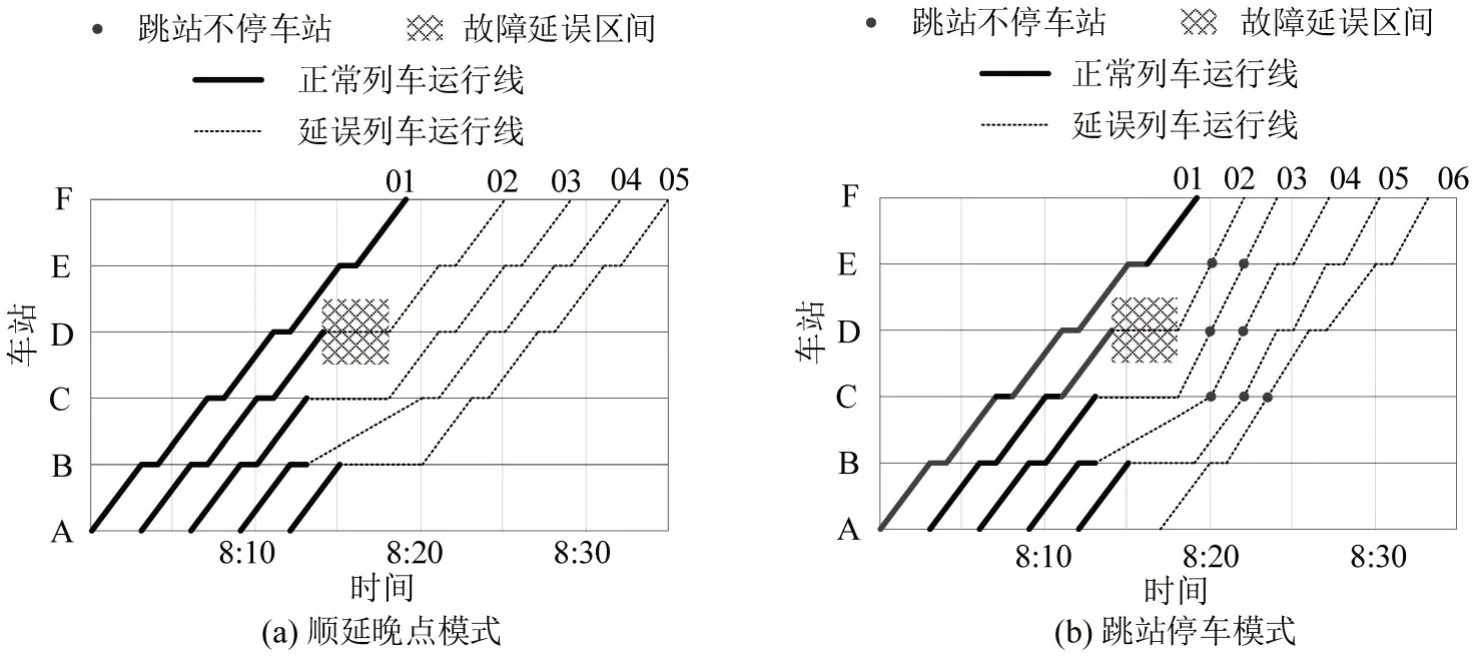
图1 列车延误后的调度措施Fig.1 Dispatching measures after train delay

1.2 客流协同控制问题

突发延误下的城轨列车调整和客流控制存在耦合关系，故调度工作必须协同考虑客流的组织。如图2(a)所示，如果不采取客流管控措施，上游车站A、B的乘客将优先占用列车资源，导致下游C、D站的乘客大量滞留。在突发延误情况下，这不仅大幅降低下游车站乘客的服务水平，还有可能导致过度拥挤造成危险。如果采取图2(b)所示的多车站客流协同控制措施，可使各站客流更加均衡，对乘客而言也更公平。

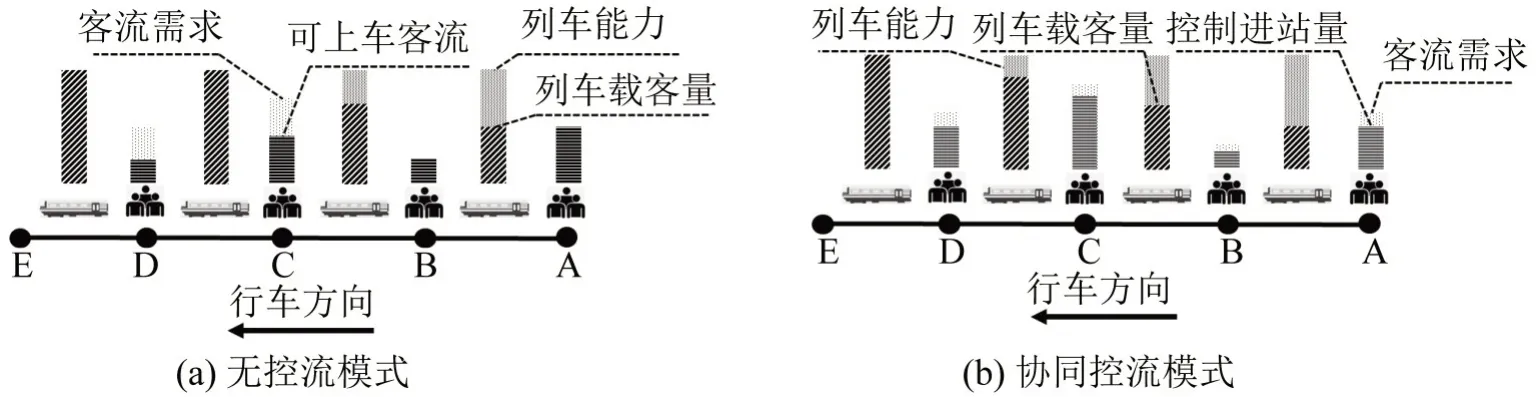
图2 客流控制措施影响Fig.2 Influence of passenger flow control measures

2 模型构建

本文构建双层规划模型来刻画行车组织与客流组织问题间存在的耦合关系。上层列车调整模型以列车到达延误最小为目标，以列车载客能力为约束，为客流提供出行时空网络；下层客流控制模型以上车乘客总量最大为目标，以列车载客能力和各车站限流率均衡为约束，使客流对应网络调整重新分布。上下层模型均为线性，具体内容如下。

2.1 模型假设及变量符号

本文模型做如下假设：

(1)进站客流需求可通过历史AFC 数据获取。突发延误持续时间通常为3～15 min，在此背景下进站客流量可认为与历史数据差异较小。

(2)调整开始阶段已在车乘客数量已知。目前，已有轨道称重、视频检测等手段对列车载客量进行估算，故本文假设该数据已知。

(3)如果某列车通过A 站不停车，对于列车调整开始前已在车去往A 站的乘客将在A 站之前的最后一次停站处提前下车等候下次列车；对于列车调整开始后进站的乘客，如果其目的地为A 站，将原地等待下次在A站停站的列车。

为便于描述，本文模型的变量及参数定义如表1所示。

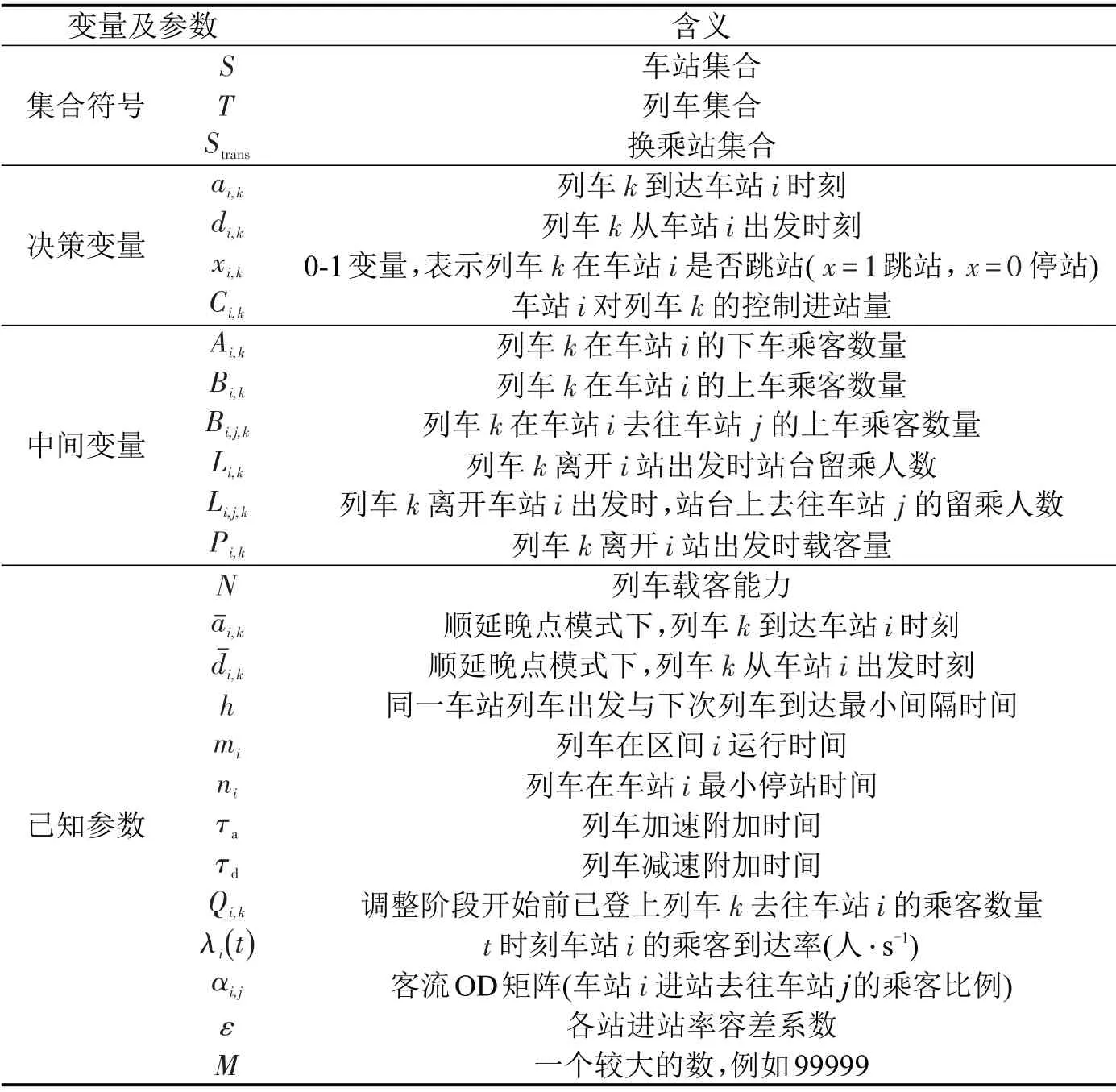
表1 变量及参数定义Table 1 Definition of variables and parameters

2.2 上层列车调整模型

上层列车调整模型以列车到达时刻ai,k、列车出发时刻di,k、列车是否跳站xi,k为决策变量，以列车到达延误最小为目标函数，即

上层模型约束条件为

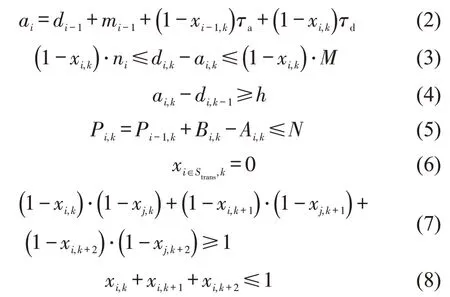
式(2)为列车运行时间约束，即列车到达时刻为前一站出发时刻与区间运行时间、加减速附加时间(如果有停站)之和。式(3)为列车停站时间约束，若xi,k=1，即列车k在车站i跳站不停车，此时列车k在车站i的到达和出发时刻相同；若xi,k=0，即列车k在车站i停站，此时列车出发时刻至少应距离到达时刻一个最小停站时间。式(4)为列车追踪间隔约束，列车k在车站i的到达时刻应和该站前一列车的出发时刻保持最小间隔h。式(5)为列车能力约束，表示各列车在各区间的载客量均不能超过列车容量，其中，Bi,k、Ai,k由下层模型的最优解获得。式(6)表示换乘站不可跳站。式(7)为跳站次数约束，为减少乘客留乘次数，本文限定任意OD 乘客最多经历2 次列车在出发站或目的站不停车。(1-xi,k)·(1-xj,k)=1 表示列车k同时在车站i和j停站，式(7)保证了每3列列车中至少有1列可以满足任意OD 的乘客需求。显然，式(7)为非线性约束，为方便后续求解，将式(7)近似线性化为式(8)，证明过程参见文献[3]。

2.3 下层客流协同控制模型

下层客流协同控制模型以各车站、各车次的控制进站量Ci,k为决策变量，以总上车客流量最大为目标函数，即

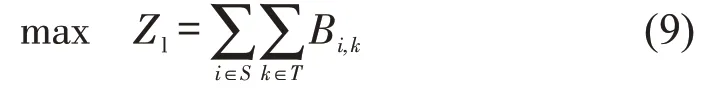
下层模型约束条件为

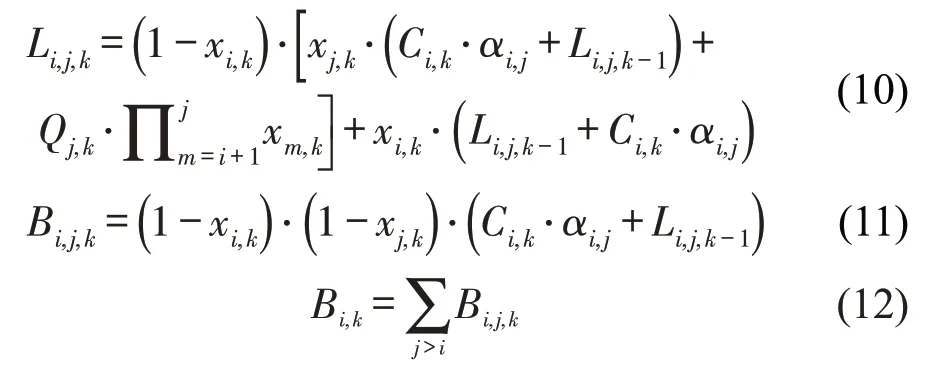
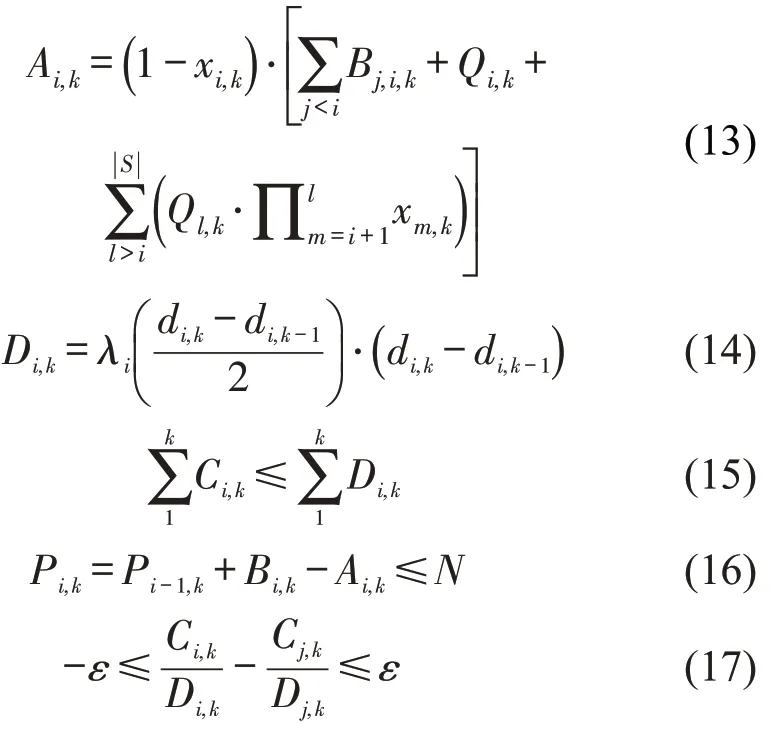
式(10)表示留乘数量，若xi,k=0，列车k在车站i停站，则留乘数量为因跳站不可达客流量；若xi,k=1，列车k在车站i跳站，则留乘数量为上次列车留乘和本次列车进站客流量之和。式(11)和式(12)表示上车乘客数量。式(13)表示下车乘客数量，为正常下车客流和因目的车站不可达而提前下车客流之和。式(14)表示客流需求。式(15)为限流进站量约束，即各车站累计进站客流量不能超过累计的实际客流需求。式(16)为列车能力约束，表示各列车在各区间的载客量均不能超过列车容量。式(17)为控流率均衡约束，即各车站对应各列车控制进站率的差异不能超过一个给定的参数ε，以此保障各车站乘客的公平性。

3 求解算法

文献[6]指出，即使是简单的双层线性规划也是NP-hard 问题，不存在多项式求解算法。一种简单的求解思路是将双层规划问题转化为单层规划，例如把下层模型替换为其KKT(Karush-Kuhn-Tucker conditions)条件，进而转化为单层规划问题。但就本文模型来看，如果将下层模型以其KKT 条件替换，得到的将是一个混合整数非线性规划模型，求解过程复杂难以满足实时调度需求。根据本文模型上下层分别保持线性的特点，若能对上下层分别求解，并利用下层模型对上层变量的近似反应函数不断迭代，则可实现快速求解。

基于灵敏度分析的算法[7]符合这一求解思路。该算法是一种迭代算法，利用下层规划对上层变量的导数信息来近似逼近反应函数，然后把这个近似反应函数代入上层规划，对从上层问题求出的最优解再一次求解下层问题就可得到新的解。重复上述步骤，得到一组新的近似反应函数。如此迭代计算，最后收敛于双层规划模型的最优解。算法流程如下：

Step 1 令迭代次数π=0，给定上层决策变量的初始解xπ=0。

Step 2 将给定的xπ带入下层规划，求解得到下层模型的最优解yπ。

Step 3 利用灵敏度分析法计算下层问题最优解yπ对上层变量xπ的导数，进而得到线性近似反应函数为

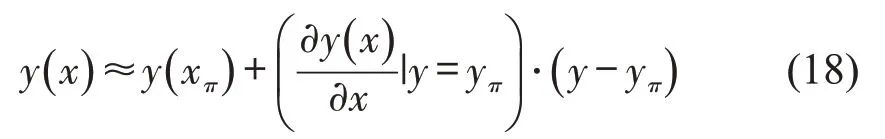
Step 4 计算式(18)，并将其带入上层规划中，求解上层问题，得到一组新的解xπ+1。

Step 5 若满足一定迭代精度，则停止；否则，令π=π+1，转Step 2。

4 案例分析

4.1 案例及模型参数

实验案例如图3所示，7:52 北京地铁亦庄线上行方向万源街站至旧宫站区间信号故障持续5 min无法行车，导致02、03、04次列车分别在万源街站、荣京东街站、荣昌东街站待避；7:57故障排除，列车按照调整后的运行图恢复行车。为验证模型算法的可靠性，本文进行4 组对照试验，分别为顺延晚点无客流控制(案例1)、仅客流控制无列车调整(案例2)、仅列车调整无客流控制(案例3)、列车调整与客流控制协同优化(案例4)，调整车次为02、03、04。

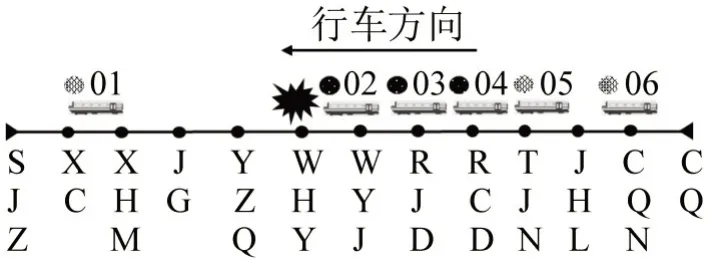
图3 北京地铁亦庄线故障案例Fig.3 Case of Beijing Subway Yizhuang Line delay

参数取值方面，列车载客能力N=1460 人，同车站列车发到间隔h=180 s，列车加、减速附加时间τa、τd均取为10 s，列车最小停站时间ni=30 s。客流数据通过历史AFC 数据获取，客流到达率λi(t)及OD比例αi,j分别如表2和表3所示。调整开始前，各列车已在车乘客数Qi,k去往终点站宋家庄(SJZ)为500 人，去往其他各站设置为100 人。客流控制方案中，各站控流容差率ε=10%，大数M=99999。

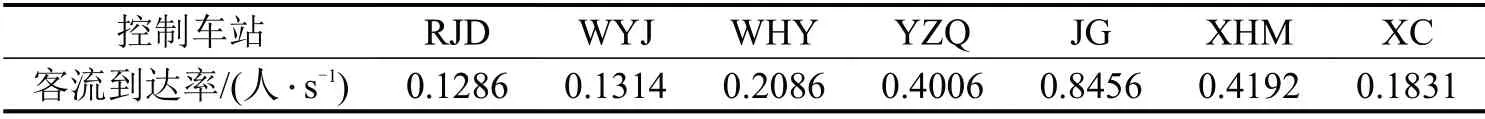
表2 控制车站客流到达率Table 2 Passenger flow arrival rate of controlled stations

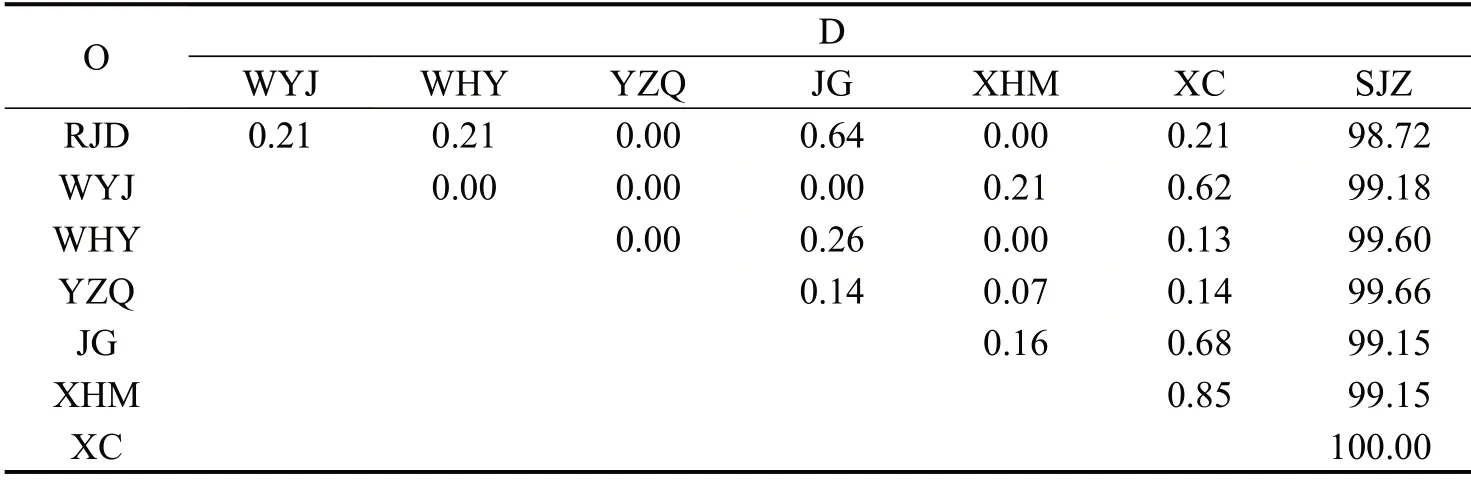
表3 进站客流OD比例矩阵Table 3 OD proportion matrix of inbound passenger flow (%)

4.2 结果分析

行车组织方面，调整后列车运行图如图4所示。案例1、2顺延晚点模式下，调整车次平均行程时间为1890 s；案例3、4跳站停车模式下，调整车次平均行程时间均为1791 s，相较于案例1、2 缩短了5.2%。在式(8)约束下，案例3、4 跳站次数均为7次，各列车在各车站的到达时刻相较于顺延晚点模式累计缩短1200 s，既提高了列车周转效率，又为乘客节约了时间。

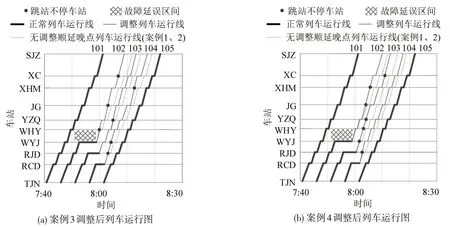
图4 调整后列车运行图Fig.4 Rescheduled train diagram

客流控制方面，选取上车客流量、进站率方差等指标对比各调度策略，如表4所示。无控制措施(案例1)的上车客流量最大；仅采取客流控制的案例2虽然降低了乘客集散量，但可使各车站进站率的方差降低97.8%，提高了各站乘客的公平性；案例3、4的跳站停车措施降低了上车客流量，在相同的跳站次数下，采取客流控制措施的案例4相较于无控制措施的案例3 不仅将上车客流量提高了6.1%，还使进站率方差降低了99.2%。综合来看，采用列车跳站与客流控制协同优化的案例4 兼顾了行车秩序的恢复和乘客出行的体验，且176.03 s的求解时耗在延误5 min的背景下能够满足实际调度需求。

表4 实验案例结果Table 4 Experimental case results

5 结论

城市轨道交通频发的列车延误不仅严重影响行车秩序，还会给乘客出行带来诸多不便。本文以跳站停车和客流协同控制为手段构建双层规划模型对突发延误后的城轨运输组织进行优化，并利用灵敏度分析算法求解。通过北京地铁亦庄线的延误案例验证本文方法的有效性。结果表明：(1)采取多车站协同控流措施可以提高各站乘客的公平性；(2)采取跳站停车的行车组织方案可以加快行车秩序的恢复，但会在降低乘客输送能力的同时加剧各站乘客的不公平；(3)采取跳站停车与多车站客流协同控制，可在保障乘客公平性的条件下提高列车运行和乘客集散效率。