政府主导下公铁联运系统三方演化博弈研究

徐新扬，杨扬

(昆明理工大学，交通工程学院，昆明650500)

0 引言

公铁联运可以充分发挥公路与铁路运输的优势，具有成本低，效率高及低碳排放的优势。在发达国家，多式联运已经成为物流行业最主要的运输方式，其中公铁联运已发展了数十年之久。目前，我国出台多项政策促进公铁联运发展，但仍有部分地区发展较慢或发展停滞，究其原因，主要是物流基础设施与信息平台的缺失，以及地方政府对于国家政策推行力度的欠缺。同时，公路运输企业与铁路运输企业的合作意愿也是影响公铁联运发展的重要因素。现阶段，公路运输企业大多存在非法改装，超载超限的运输现状，以达到获取额外收益，降低铁路比较优势的目的；铁路运输企业虽然有着运量大，能耗低的优势，但由于无法完成末端配送，需要付出额外成本对接公路运输企业完成运输订单。而公铁联运“一单制”模式可以发挥公铁企业双方优势。因此，如何实现共赢，协调公铁联运系统内各主体的利益，是公铁联运发展亟待解决的关键问题。

对公铁联运策略的研究主要集中于定价与补贴政策，其中博弈论被广泛运用到研究中。如HANG Z.等[1]针对公铁联运网络设计与定价策略问题建立竞争博弈模型。张桐等[2]对公铁联运模式与传统公路货运的定价策略进行博弈研究。文献[3]利用流动博弈理论对公铁联运的潜力进行预测。针对政府补贴政策对公铁联运影响的分析，文献[4-5]基于LAMBIT 模型，文献[6]基于Marco-scan 模型，结果认为补贴政策对促进公铁联运发展效果明显。文献[7]分析补贴政策对公铁联运发展的促进力度，认为当补贴力度超过0.14元·(t·km)-1后对公铁联运发展的促进力度并不明显。针对公铁联运竞争力的研究，唐继孟等[8]构造货物运输广义费用模型，分析枢纽延误对公铁联运竞争力的影响。对公铁联运系统的研究不能只分析公铁运输企业两方，段华薇等[9]与李芳等[10]分别加入铁路物流中心与大宗商品集仓研究公铁联运物流服务供应链协调与一体化模式构建。

公铁联运策略研究多从个体或双方策略进行定价或离散数学模型研究，较少从系统的角度进行整体研究，补贴政策也较多以托运人为对象。本文在对公铁运输企业实施相应政策背景下，研究公铁联运系统的稳定性与参与者的交互影响，建立由地方政府、公路运输企业、铁路运输企业3 个博弈主体构成的公铁联运系统，分析系统内部稳定性与各博弈主体演化趋势，并剖析政府行为对系统演化的影响，探寻公铁联运模式运作理想化的条件。

1 模型构建

1.1 符号说明

Ch2、Cr2——公路、铁路运输企业不进行公铁联运时的运输成本；

Ih2、Ir2——公路、铁路运输企业不进行公铁联运时的运输收益；

Eh2——公路运输企业选择不合作策略时由于超限超载获得的额外收益；

α——地方政府对于公路运输企业选择不合作策略时非法改装，超限超载行为的监管强度；

P——铁路运输企业不进行公铁联运时末端公路运输的额外支出；

S——公路与铁路运输企业均选择合作时为政府带来的社会收益；

Wh1、Wr1——公铁联运时公路、铁路运输企业的运输成本；

Nh1、Nr1——公铁联运时公路、铁路运输企业的运输收益；

Qh1、Qr1——公路与铁路运输企业选择合作策略时建设一体化物流信息平台的额外成本；

Vg1——地方政府选择积极推进政策时建设公铁联运基础设施的成本；

Vh1、Vr1——地方政府选择消极推进政策时选择合作策略的公路、铁路企业建设公铁联运基础设施的成本；

Fh2——地方政府对公路运输企业违规行为的罚款；

Fg2——地方政府选择消极推行政策策略时形象下跌导致的损失；

Mh1、Mr1——地方政府选择积极推行政策策略时给予公路、铁路运输企业中选择合作策略企业的补贴；

T——地方政府选择积极推行政策策略时国家给予地方政府的奖励；

K——地方政府积极推进政策时选择不合作策略运输企业督导考评不合格造成的损失。

1.2 模型假设

为构建演化博弈模型，作如下假设：

(1)由地方政府、公路运输企业、铁路运输企业构建公铁联运系统，3个博弈主体均具有有限理性，各主体间信息不对称，博弈随机且行为交互影响。

(2)博弈主体行为策略，地方政府策略集g表示政府是否积极推进公铁联运政策，g={g1,g2} ，其中，g1为积极推进，g2为消极推进；公路运输企业策略集h与铁路运输企业策略集r表示公铁运输企业是否选择公铁联运模式合作，h={h1,h2} ，r={r1,r2} ，其中，h1，r1为合作，h2，r2为不合作。

(3)博弈系统各主体均有一定概率选择自己的行为，假设初始状态下，地方政府选择积极推进的概率为pg1，消极推进的概率为pg2，pg2=1-pg1；公路运输企业选择合作的概率为ph1，选择不合作的概率为ph2，ph2=1-ph1；铁路运输企业选择合作的概率为pr1，选择不合作的概率为pr2，pr2=1-pr1。

(4)地方政府积极推行政策时，只对选择合作策略的运输企业给予补贴。公路与铁路运输企业中只要有一方选择不合作策略，则公铁联运模式无法进行；当公路运输企业选择合作策略时，即便铁路运输企业选择不合作策略使公铁联运无法进行，默认公路运输企业也不会通过非法改装，超限超载等方式获取额外收益。

1.3 收益矩阵

根据问题描述与模型假设，得到公铁联运系统中三方博弈收益矩阵，如表1所示。

表1 三方博弈主体的收益矩阵Table 1 Profit matrix of subject of tripartite game

2 演化博弈分析

2.1 复制动态方程

公铁联运系统中各主体策略的动态变化是有限理性博弈分析的核心，动态变化速度是关键问题，故分别构造地方政府、公路运输企业及铁路运输企业的复制动态方程，描述各主体策略被选择的频率，即表示各方主体选择不同策略比例的动态变化速度。

(1)地方政府的收益期望函数与复制动态方程

根据表1博弈收益矩阵分析可知，地方政府选择“积极推进”的期望收益f(g1)为

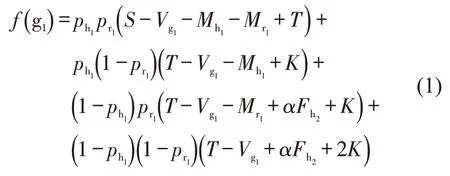
地方政府选择“消极推进”策略的期望收益f(g2)为

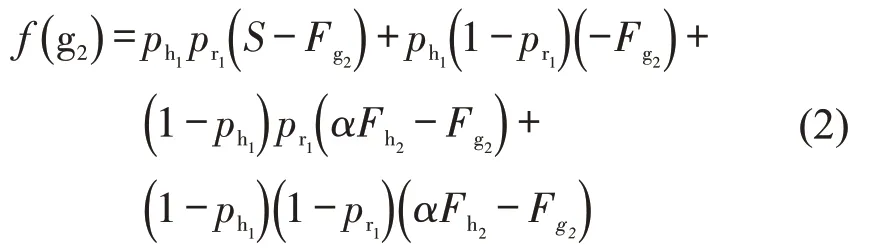
则地方政府的平均收益f()为

根据Malthusian 动态方程，构建地方政府的复制动态方程F(pg)为

(2)公路运输企业的收益期望函数与复制动态方程

根据表1博弈收益矩阵分析可知，公路运输企业选择“合作”的期望收益f(h1)为

公路运输企业选择“不合作”策略的期望收益f(h2)为

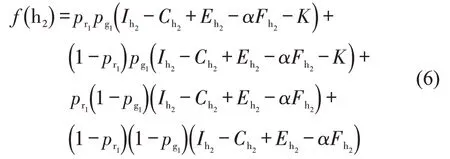
则公路运输企业的平均收益f()为

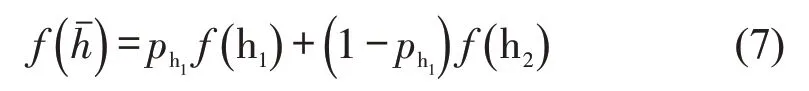
根据Malthusian 动态方程，构建公路运输企业的复制动态方程F(ph)为

(3)铁路运输企业的收益期望函数与复制动态方程

根据表1博弈收益矩阵分析可知，铁路运输企业选择“合作”的期望收益f(r1)为

铁路运输企业选择“不合作”策略的期望收益f(r2)为

则铁路运输企业的平均收益f()为

根据Malthusian 动态方程，构建铁路运输企业的复制动态方程F(pr)为

2.2 稳定性分析

根据RITZBERGER K.[11]演化博弈均衡求解方法，令公铁联运系统各主体动态复制方程为0，即联立式(4)、式(8)和式(12)，令其为0，求得公铁联运系统的平衡点。

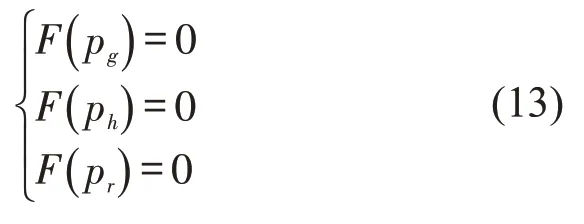
根据文献[11]求解式(13)，得到并只需讨论8个特殊均衡点：(0,0,0)、(0,0,1)、(0,1,0)、(0,1,1)、(1,0,0)、(1,0,1)、(1,1,0)、(1,1,1)的稳定性，即可研究公铁联运三方博弈系统的稳定性，其余均为非渐进稳定状态。

根据李雅普诺夫稳定性理论，通过对公铁联运系统博弈三方主体的复制动态方程，即式(4)、式(8)和式(12)求偏导，得到雅可比矩阵，分析矩阵在每个均衡点的特征值，判断公铁联运系统的渐近稳定性。雅可比矩阵J为

将8个特殊均衡点分别代入雅可比矩阵中，根据矩阵特征值求法得到相应的特征值λ1、λ2、λ3，如表2所示。

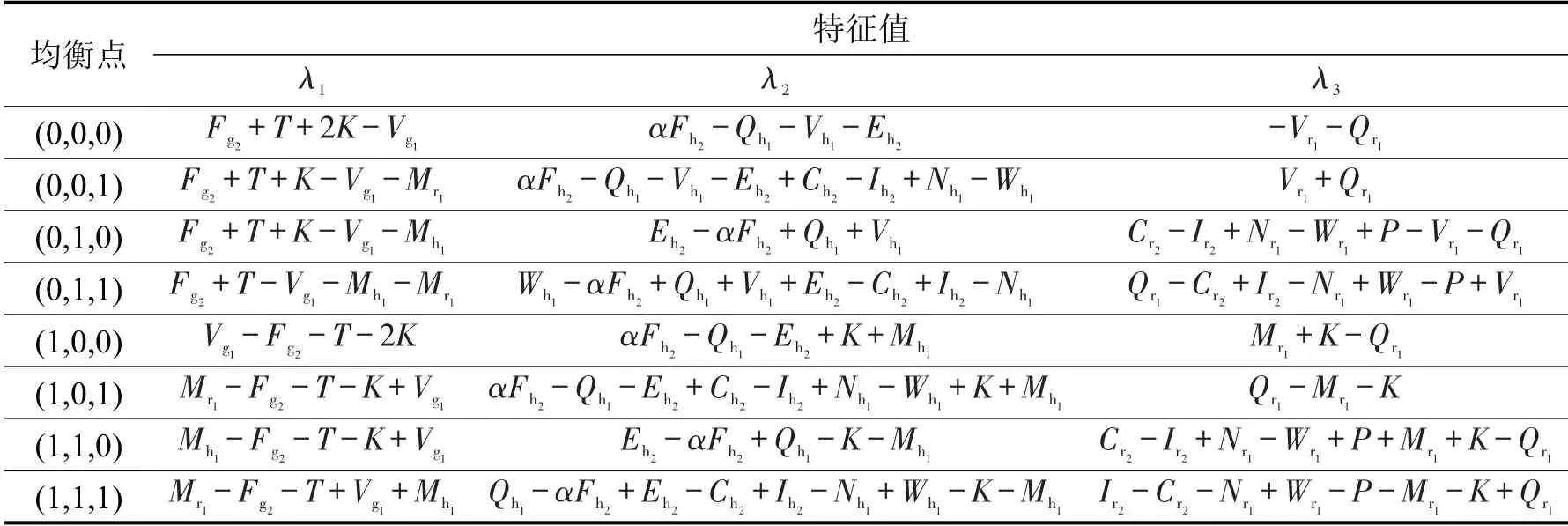
表2 博弈系统各均衡点特征值Table 2 Eigenvalues of each equilibrium point of game system

根据李雅普诺夫判别法(间接法)，当雅可比矩阵的所有特征值λ ＜0 时，该均衡点为渐进稳定点，为汇；当雅可比矩阵中所有特征值λ ＞0 时，该均衡点为不稳定点，为源；当雅可比矩阵中特征值λ中存在有正有负时，该均衡点为不稳定点，为鞍点。由表2可得：(0,0,1)只能是不稳定点，因为λ3=Vr1+Qr1＞0 恒成立。均衡点稳定条件如表3所示。

满足表3稳定性条件情况下，(0,0,0)、(0,1,0)、(0,1,1)、(1,0,0)、(1,0,1)、(1,1,0)、(1,1,1)可能是进化稳定策略。

表3 均衡点稳定性条件Table 3 Equilibrium point stability condition

3 数值仿真

3.1 理想演化路径分析

根据公铁联运博弈系统稳定性分析可知，除(0,0,1)点为不稳定点外，其余7 个均衡点稳定条件各有不同，对理想策略集{积极推进，合作，合作}进行数值仿真分析。

根据稳定性条件7，设参数取值Fg2=2 ，Fh2=4 ，T=2 ，K=3 ，Vg1=1.5 ，α=0.8 ，Qh1=2 ，Qr1=3 ，Vh1=2 ，Vr1=2 ，Eh2=3 ，Mh1=0.5 ，Mr1=1.5 ，Cr2=3，Ch2=3，Ir2=4 ，Ih2=5 ，Wr1=1，Wh1=2，Nr1=1，Nh1=4，P=0.5。地方政府、公路运输企业、铁路运输企业初始策略选择概率pg1、ph1、pr1均设定为0.5，仿真演化如图1所示。

图1 公铁联运博弈系统在条件7下的演化路径Fig.1 Evolution path of game system under condition 7

由图1可知，当政府补贴与建设公铁联运基础设施的成本之和小于国家对于地方政府积极推进政策的经济奖励与地方政府消极推进政策时形象下跌导致的经济损失之和时，公路运输企业选择合作策略时，运输成本与建设物流信息平台额外成本之和小于公铁联运收益与地方政府补贴之和；选择不合作策略时，地方政府对于违规运输方式的罚款与运输企业选择不合作策略的罚款之和大于公路运输企业不合作策略时的额外收益。铁路运输企业选择合作策略时，运输成本与建设物流信息平台额外成本之和小于公铁联运收益与地方政府补贴之和；选择不合作策略时，收益小于运输成本与末端公路运输额外支出与地方政府对于不合作策略的罚款之和。此时，公铁联运博弈系统演化路径为{积极推进，合作，合作 }，(1,1,1)为进化稳定策略。

3.2 各主体初始意愿对演化结果的影响

由复制动态方程可知，公铁联运系统内某一方主体演化路径受其他主体初始策略意愿影响，考虑系统演化路径分析时pg1、ph1、pr1均设定为0.5 的单一性，变化参数数值，研究初始意愿对演化结果的影响。

(1)ph1、pr1变化对地方政府演化影响

以0.5为初始策略选择意愿的中间值，高于0.5为高意愿，低于0.5为低意愿，将公路运输企业与铁路运输企业初始意愿值分别取0.1 与0.9，其中，0.9代表高意愿，0.1 代表低意愿。并将公路运输企业与铁路运输企业初始选择概率组合分为：(高，高)、(低，低)、(高，低)、(低，高)这4 种方式，研究对地方政府演化路径的影响，结果如图2所示。

由图2可知，无论ph1、pr1初值组合如何变化，不会影响地方政府向积极推进政策的路径演化，即选择积极推进策略的选择概率终将演化至1。但ph1、pr1初值的组合变化影响着地方政府收敛于选择积极推进策略的速率，影响强度从高到低的ph1、pr1初值意愿组合分别是：(低，低)，(高，低)，(低，高)，(高，高)，说明公铁运输企业参与公铁联运的意愿与地方政府积极推进政策的概率成反比，铁路运输企业的低合作意愿略比公路运输企业的低合作意愿更能刺激政府积极推动公铁联运政策。

图2 ph1、pr1 数值变化对地方政府策略演化的影响Fig.2 Effect of changes in ph1 and pr1 values on evolution of local government strategies

(2)pg1、pr1变化对公路运输企业演化影响

研究地方政府与铁路运输企业初始选择概率组合(高，高)、(低，低)、(高，低)、(低，高)这4种意愿方式对公路运输企业演化路径的影响，结果如图3所示。

图3 pg1、pr1 数值变化对公路运输企业策略演化的影响Fig.3 Effect of changes of pg1 and pr1 on evolution of highway transportation enterprises

由图3可知，pg1、pr1初值组合变化会影响公路运输企业的选择概率，当地方政府与铁路运输企业的初始意愿组合为(高，高)、(高，低)时，公路运输企业对于合作策略的选择概率趋向于1；当地方政府与铁路运输企业的初始意愿组合为(低，高)、(低，低)时，公路运输企业对于合作策略的选择概率趋向于0。同时，pg1、pr1初值的组合变化并不会影响公路运输企业选择概率演化的速率，但地方政府积极推进政策的意愿决定着公路运输企业是否选择合作策略。当地方政府高意愿积极推进政策时，公路运输企业向合作策略收敛；当地方政府低意愿积极推进政策时，公路运输企业向不合作策略收敛。铁路运输企业的合作意愿无法影响公路运输企业的演化趋势。

(3)pg1、ph1变化对铁路运输企业演化影响

研究地方政府与公路运输企业初始选择概率组合(高，高)、(低，低)、(高，低)、(低，高)这4种意愿方式对铁路运输企业演化路径的影响，结果如图4所示。

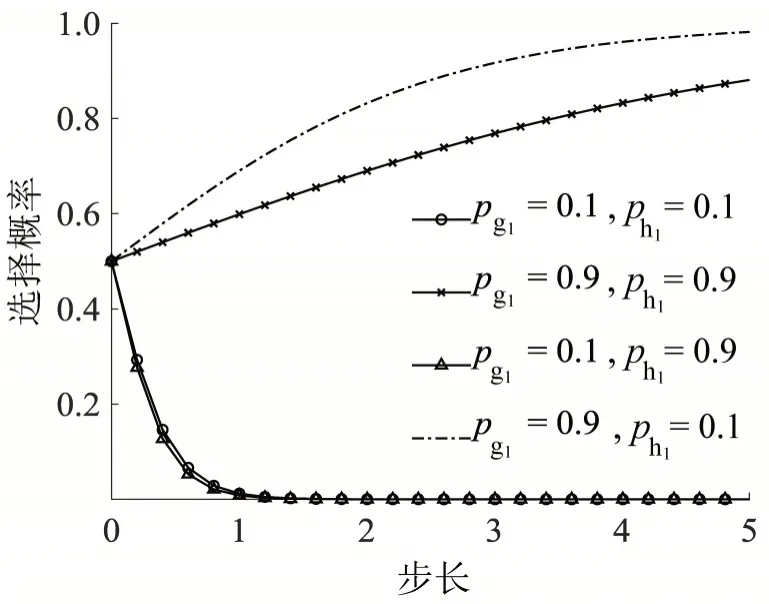
图4 pg1、ph1 数值变化对铁路运输企业策略演化的影响Fig.4 Impact of changes in pg1 and ph1 values on evolution of railway transportation enterprises

由图4可知，pg1、ph1初值组合变化会影响铁路运输企业的选择概率，当地方政府与公路运输企业的初始意愿组合为(高，高)、(高，低)时，铁路运输企业对于合作策略的选择概率趋向于1；当地方政府与公路运输企业的初始意愿组合为(低，高)、(低，低)时，铁路运输企业对于合作策略的选择概率趋向于0。pg1、ph1初值的组合变化还会影响铁路运输企业选择概率演化的速率，当地方政府高意愿采取积极推进策略时，公路运输企业合作的意愿越高，铁路运输企业向合作策略选择概率演化的速率越快；当地方政府低意愿采取积极推进策略时，公路运输企业合作的意愿越高，铁路运输企业向不合作策略演化的速率越快。由此可知，地方政府积极推进政策是铁路运输企业进行公铁联运的前提，公路运输企业选择合作策略的意愿不会影响铁路运输企业的演化趋势。当地方政府高意愿推进政策时，铁路运输企业收敛于合作策略的速率与公路运输企业选择合作策略的意愿成反比。

3.3 政府行为对演化结果的影响

演化博弈中额外成本增加，合作收益减少或不合作收益大于合作收益时，各主体向(1,1,1)演化的速率将减慢是毋庸置疑的。因此，本文分析政府行为对公铁联运系统演化结果的影响，探索公铁联运系统内部演化机理。

(1)补贴政策对各主体演化影响

以条件7参数取值为基础，对Mh1与Mr1分别取值0.7、0.8、0.9，研究其对博弈系统内各主体演化趋势的影响，如图5和图6所示。

图5 Mh1、Mr1 数值变化对地方政府演化影响Fig.5 Effect of changes in Mh1 and Mr1 values on evolution of local government strategies

由图5和图6可知，在稳定性条件7下，地方政府补贴力度的改变不影响公路与铁路运输企业合作策略的选择概率演化趋势，公铁运输企业对于合作策略的选择概率均趋向于1，补贴力度仅改变公铁运输企业策略演化的速率。地方政府对公铁运输企业的补贴越高，公铁运输企业向合作策略演化的速度越快，虽然地方政府向积极推进政策策略演化的速度相对变慢，但整体演化趋势差别不大，说明补贴政策对公铁联运起明显的促进作用。

图6 Mh1、Mr1 数值变化对公铁运输企业演化影响Fig.6 Effect of changes of Mh1 and Mr1 on evolution of highway and railway transportation enterprises

(2)政府督导考评力度对系统演化影响

K分别取值3、4、5，分析不同取值下公铁联运博弈系统演化变化，如图7所示。

图7 K 值变化对公铁运输企业演化影响Fig.7 Effect of changes of K on evolution of highway and railway transportation enterprises

由图7可知，在稳定性条件7下，地方政府督导考评强度的改变不影响公路与铁路运输企业合作策略的选择概率演化趋势，公铁运输企业对于合作策略的选择概率均趋向于1，督导考评强度仅改变公铁运输企业策略演化的速率。政府督导考评强度增加，会加快公铁运输企业向合作策略演化的速率，铁路运输企业相较于公路运输企业对地方政府督导考评政策更敏感。

(3)违规监管强度与罚款对公路运输企业演化影响

α分别取值0.5、0.6、0.7，Fh2分别取值4、5、6，分析不同取值下公铁联运博弈系统演化变化，如图8所示。

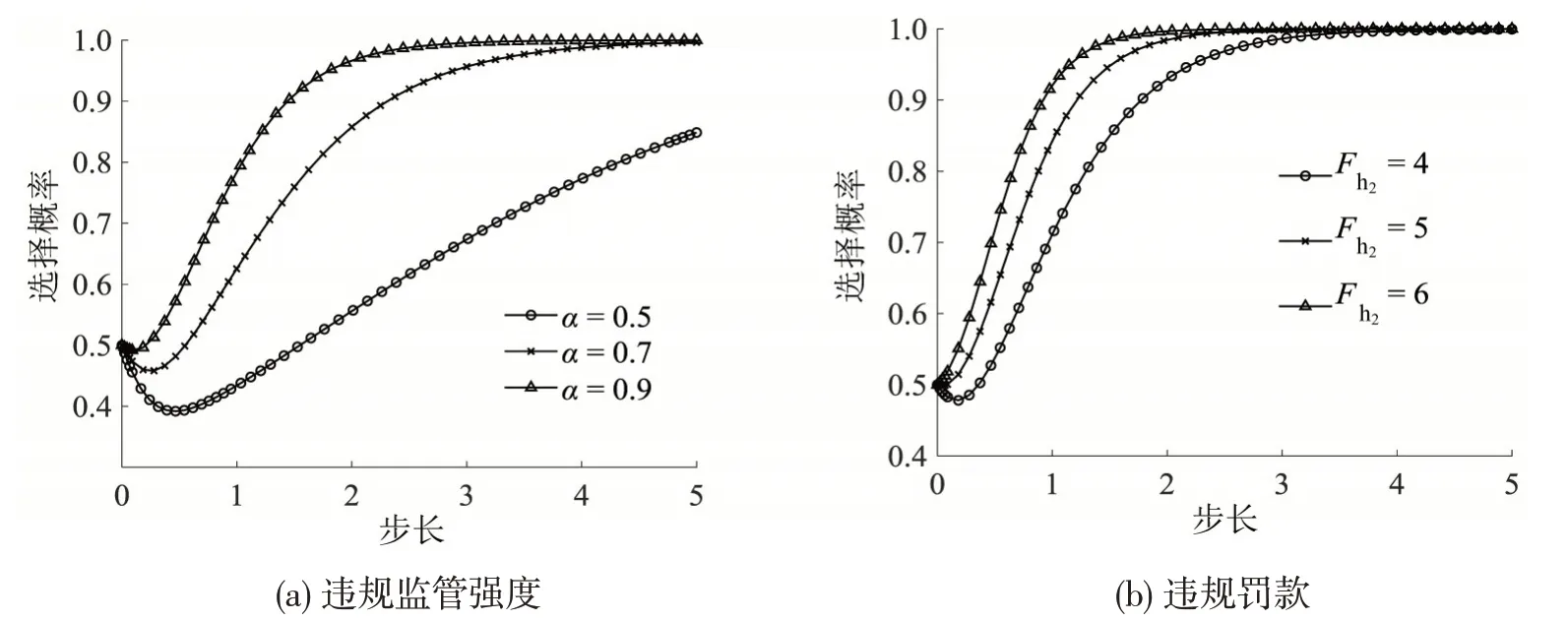
图8 α、Fh2 值变化对公路运输企业演化影响Fig.8 Effect of changes of α and Fh2 on evolution of highway transportation enterprises

由图8可知，在稳定性条件7下，地方政府违规监管强度与罚款的改变不影响公路与铁路运输企业合作策略的选择概率演化趋势，公铁运输企业对于合作策略的选择概率均趋向于1，违规监管强度与罚款仅改变公铁运输企业策略演化的速率。地方政府对于公路运输企业违规行为的监管强度，以及违规罚款与公路运输企业向合作策略收敛的速率成正比，高强度的监管促进公路运输企业进行公铁联运。

(4)形象下跌对地方政府演化影响

Fg2分别取值1、2、3，分析不同取值下公铁联运博弈系统演化，如图9所示。

图9 Fg2 值变化对地方政府演化影响Fig.9 Effect of changes in Fg2 values on evolution of local government strategies

由图9可知，在稳定性条件7下，地方政府形象下跌损失的改变不影响地方政府积极推进策略的选择概率演化趋势，地方政府对于积极推进策略的选择概率均趋向于1，形象下跌仅改变地方政府策略演化的速率。政府消极推进政策时，因形象下跌导致的损失与地方政府向积极推进策略演化的速率成正比。

4 结论

本文构建公铁联运三方博弈系统，分析系统内部稳定性，着重研究初始意愿变化，以及政府主导下不同政策对公铁联运博弈系统演化的影响，得出如下结论：

(1)除(0,0,1)点不稳定外，博弈系统具有7 个稳定条件下的均衡点，达到理想状态(积极推进，合作，合作)的稳定性条件为：Mr1-Fg2-T+Vg1+Mh1＜0 ，Qh1-αFh2+Eh2-Ch2+Ih2-Nh1+Wh1-KMh1＜0，Ir2-Cr2-Nr1+Wr1-P-Mr1-K+Qr1＜0。

(2)地方政府选择积极推进政策的初始意愿决定着公铁运输企业是否选择合作策略，当地方政府对积极推进政策展现出高意愿，无论公铁联运企业中一方合作意愿的高低，另一方都将向合作策略进行演化。

(3)公铁运输企业各自的合作意愿与演化路径不受彼此初始合作意愿干扰，主要由政府初始积极推进政策意愿决定，铁路运输企业的低合作意愿比公路运输企业的低合作意愿更能刺激政府积极推动公铁联运政策。

(4)地方政府的补贴政策明显促进公铁运输企业向合作策略演化的速率，地方政府演化速率对补贴政策的敏感度不高。高强度的督导考评与违规运输监管力度是发展公铁联运的有效政策，随着强度的增加，公铁运输企业向合作策略演化的速率大大增加。政府形象的下跌是地方政府积极推进公铁联运政策的重要因素。