基于个体出行链的区域城际铁路规划方法研究

李岸隽，王典，彭其渊*

(西南交通大学，a.交通运输与物流学院；b.综合交通运输智能化国家地方联合工程实验室，成都611756)

0 引言

我国高速铁路逐渐成网，铁路骨干网络已基本形成，研究城市群内的城际铁路规划逐渐成为热点。甘超[1]基于节点重要度和城市经济关联度提出成渝城市群城际铁路网构架。黄超[2]进一步基于网络演化思想优化线网结构，以加强线网密度较低区域的线路连接。苏瑞晔[3]从时空可达性角度提出城际铁路线网规划模型，最小化线网不可达OD的数量。上述研究均基于城镇节点进行建模，无法体现旅客全出行链，规划结果只能满足节点之间的连通性，可能导致高铁(城际)站离市区远、旅客“门到门”出行时间长等现实问题。近年来，“Mobility as a Service (MaaS)”的概念在学术界和工业界逐渐流行，可理解为出行即服务、基础设施即服务。“MaaS”理念包含多模式交通的运输供给、公共运输的“最后一公里”、个体行为特征等要素[4]。这对铁路骨干网成型后，精细化规划很有借鉴意义。首先，轨道交通的可达性必须通过开行列车来实现，若没有列车开行或运输能力小于运输需求，则无法满足出行者需求；其次，大多数旅客需要利用城市内的交通方式完成城际铁路两端的接驳，对客流的把握不应局限在“站到站”的运输，而应考虑旅客出行全过程，将“以人为本”的规划理念体现在完整出行链的构建。

随着移动设备的普及和大数据等技术的发展，结合智能手机、地理信息、交通调查、统计调查等多源数据捕捉个体出行需求成为可能[5]。因此，本文提出基于个体特征的城际铁路规划模型，优化得到使网络中出行者的广义费用和投资费用加权和最小的最优建设方案。在建模时考虑出发地或目的地与城际铁路车站间的多模式交通集散，以及出行者个体差异、交通工具个体差异和服务供给时间窗等因素，精准规划适应个体需求的全出行链，有利于掌握潜在客流需求，使交通基础设施的规划能紧密联系运输服务供给和旅客出行需求。

1 带时间窗的多模式出行链构建

为准确描述带时间窗的运输服务供给和旅客出行需求，需要构建一个包含地铁、城市道路、城际铁路等多种交通方式、所有已建和未建物理路段的多模式时空网络。其中，未建路段可根据实际客流、土地利用等客观情况提出若干条待决策路段Ec，以保证所得方案的实用性。对任一出行者p∈P(P为出行者集合)，其城际出行链可表示为时空网络中的时空路径。根据其时间价值λp寻找其出发地op至目的地dp间所有满足期望出行时间窗[tp,ed,tp,la] 的可行时空路径，进而通过优化模型决策最优建设方案并分配路径。

1.1 带时间窗的时空网络构建

从基础设施角度，一个运输物理网络由若干节点i,j和路段()i,j组成，常被抽象为有向图。为完整描述出行全过程，将各类交通方式描述为独立的物理站点，各物理站点还细分为场站出入口和完成乘降动作的两个独立物理点，交通工具只能在乘降点间完成运输任务。以图1为例：一个城际运输物理网络由14 个节点和13 个路段组成，包含3 类节点和3类路段；地铁列车在路段(3,4)和路段(11,12)提供服务，城际列车在路段(7,8)提供服务；出行者在交通场站通过上下车路段完成乘降作业。

图1 区域交通物理网络示意图Fig.1 A illustration of a regional physical transportation network

从运输服务角度，除步行路段和对应自驾车/打车的乘车路段外，出行者对公共运输路段的使用还依赖运营商的服务供给。城市轨道交通、城际铁路等基础设施不仅存在物理起讫点，还存在运载工具v开展运营服务的最早发车、最晚收车时间窗[tp,ed,tp,la] 及发车间隔、列车定员等约束。对出行者p而言，也存在期望的出行时间窗[tp,ed,tp,la] ，即出行者p最早于tp,ed时刻从点op出发并期望于tp,la时刻前到达目的地dp。为描述基础设施的服务供给和旅客出行时间窗，可将物理网络拓展为可直观反映时空耦合关系的时空网络[6]。苏瑞晔[3]、Tong[6]已在交通网络设计问题研究中引入时空网络。本文在构建时空网络时，时空点(i,t),(j,s)分别表示出行者在t,s时刻经过点i,j，时空弧(i,j,t,s)表示出行者在t时刻进入路段(i,j)并在s时刻离开的活动[6]。物理路段对应的时空弧包括某个具体时间窗内的所有可实现位移，并可供出行者选择的步行弧(含上下车及换乘)和乘车弧。

此外，出行者p可能不在最早出发时间tp,ed从出发地出发，或者在最晚到达时间tp,la前已到达目的地，因此在出发点和到达点存在等待弧，这类等待时间的费用记为0。由于运输服务存在发车间隔时间，出行者在乘车点也存在等待弧，根据实际等待时间计算广义费用。由于存在期望的时间窗内出行需求无法得到满足的情况，在每个出行者的出发地和目的地间搭建从最早出发时间到最晚到达时间的虚拟弧，并赋以较大的费用，以保证出行者能实现位移。综上，一个多模式的时空网络包含步行弧(含上下车及换乘)、不同运输方式乘车弧、乘降点等待弧、起讫点等待弧、虚拟弧等5类时空弧。

1.2 基于聚类的时空出行链构建

由于个体的时间价值反映个体对出行时间和费用的敏感程度，即便是同样的出发地、目的地以及出行时间窗，对不同个体而言，广义费用最小的路径可能不同。基于个体行为研究的难点在于如何处理大规模个体。Martinez[7]提出基于聚类的小型公交服务设计问题，将上下车时空点可以兼容的乘客归为一组规划小型公交服务线网。类似聚类分析方法同样适用于铁路旅客分类[8]。本文借鉴类似聚类思想，将出行时间窗、时间价值、出发地、目的地等属性相同的出行者进行聚类。因此，同一类出行者的可行出行路径k∈Kp(Kp为出行者p的可选路径集合)相同。

如图2所示，以某类出行者为例详细说明时空出行链构建。假设其时间价值为60元·h-1，期望的出行时间窗最早为8:00出发，最晚12:00到达。在图1物理网络基础上，引入时间维度描述该类出行者时空轨迹。因存在一条实际路径满足其出行需求，故该类出行者不会选择虚拟弧完成出行。由图2可知，该类出行者在出发地、目的地和城际站均需等待。

图2 时空路径示意图Fig.2 A illustration of a space-time path

2 模型构建

2.1 基本假设

(1)假设用于城际出行需求分析的交通小区Oz,Dz及其质心已知。

(2)假设小区质心间基于个体特征的城际出行需求已知。

(3)假设各路段旅行时间、运输供给时间窗、列车发车间隔、列车定员、票价已知且固定。

2.2 参数和变量

(1)参数

c(p,k)——出行者p采用路径k的广义费用；

β——总投资费用的权重；

f(i,j)——路段(i,j)建设费用；

ri,j,t,s——时空弧(i,j,t,s)已有或预留的运输能力，ri,j,t,s ＜0 表示需求，否则为供给；

Qv(i,j,t,s)——经过时空弧(i,j,t,s)的列车载客能力；

Bv——城际列车v对应的时空弧集合；

Bp,k——寻找路径k时，满足出行者p时间窗的所有时空弧集合；

cp(i,j,t,s)——出行者p经过时空弧(i,j,t,s)的广义费用；

T(i,j)——路段(i,j)的旅行时间；

g(i,j,t,s)——经过时空弧(i,j,t,s)需要支付的实际费用。

(2)0-1变量

x(p,k)——出行者p选择路径k出行时为1，否则为0；

y(i,j)——物理网络中修建路段(i,j)时为1，否则为0；

δi,j,t,s(p,k)——路径k∈Kp(∀p∈P)包含时空弧(i,j,t,s)∈Bp,k时为1，否则为0。

2.3 优化模型

(1)目标函数

目标函数最小化所有出行者的广义总费用和总投资费用的加权和。

(2)约束条件

式(2)为对任一出行者必须且只能选择一条满足其城际出行需求的时空路径；式(3)为城际列车载客能力约束，考虑中间站客流，即ri,j,t,s；式(4)为被选择路径经过的物理路段必须修建。

2.4 备选路径集生成

求解基于时空网络的优化模型通常面临变量和约束数量极多的问题。Mahmoudi[9]在求解带时间窗的车辆路径规划问题时提出基于动态规划的最短路算法和在时空状态网络中缩小路径搜索范围的策略。鉴于此，本文先根据每类出行者的期望出行时间窗和运输服务供给时间窗，构建所有可供选择的时空弧，再基于动态规划在多模式时空网络中寻找若干条可行时空路径。通过贪心算法，每次迭代对每类出行者寻找n条可行路径并加入备选路径集合，将其代入上述优化模型，利用CPLEX求解器更新最优解，如图3所示。

图3 模型求解框架图Fig.3 Solution framework of model

在每次迭代中，对任一出行者p通过n次循环找到n条可行路径。每次循环从可供选择的时空网络中删去已被选择的城际出行时空弧，以找出若干条不同路径。每次循环寻找最优路径的模型为

(1)目标函数

式(5)最小化出行者p的广义出行费用；式(6)计算任意时空弧的广义费用。

(2)约束条件

式(7)为流平衡约束。

3 算例分析

以某双城间的城际铁路规划为例，假设出发城市和到达城市均有两个可供选择的城际铁路车站。将各城市内的交通小区质心连接至所在城市的各铁路车站用于表示城市内接驳城际铁路的交通路段，作为出行路径中的一部分。

算例中将每个城市视为一个交通小区，城际客流需求集中于小区质心点，构建包含需求点、换乘枢纽点和所有已存在、待决策路段的物理网络。为描述出行全过程，将出发地(目的地)细分为5 个物理点1～5(30～34)，分别表示出发地(目的地)、出发地(目的地)就近的城市轨道交通车站和站台、出发地(目的地)就近的道路交通场站和乘车点。同理，将每个铁路枢纽展开为6个物理点，包括点6～11、12～17、18～23和24～29，分别表示每个铁路枢纽内的城轨车站和站台、道路交通场站和乘车点、铁路车站和站台，如图4所示。由此可完整描述出行全过程以及详细描述完成各类交通方式的候乘手续所需时间及换乘时间。

图4 某区域多模式物理交通网络图Fig.4 A multimodal physical transportation network in a region

点11、17和点18、24分别表示两城市内两个铁路车站对应的乘降站台，城际铁路待决策修建路段包括(11,18)、(11,24)、(17,18)和(17,24)，假设其按不同速度标准建设，对应的旅行时间分别为150，130，100，80 min，建设费用分别为180 亿元，260 亿元，380亿元，450亿元。两城市的城市轨道交通服务时间窗均为[6:00,22:20]，在22:20 之后到达的出行者无法选乘城市轨道交通到达最终目的地。各路段的类型、旅行时间、费用如图4所示，各类路段的服务时间窗及发车间隔如表1所示，由此可构建时空网络用于规划各类出行者的时空路径。β取较小正数以减小投资费用对旅客出行需求的影响。共有9 类出行者从点1 出行到点34，分3 种场景分别优化求解最优建设方案，并将个体出行需求分配到具体出行路径。

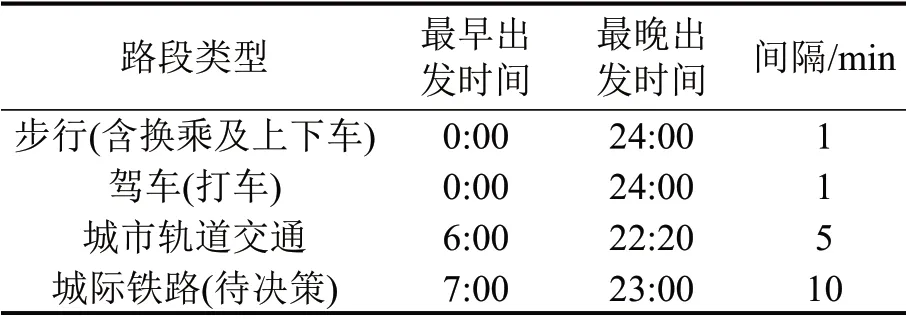
表1 各类路段时间窗及发车间隔Table 1 Link information

场景1 不考虑时间窗且不区分个体特征

假设所有出行者时间价值均为60元·h-1，则最优建设方案为建设路段(17, 24)，实际投资450 亿元。各类出行者在任何时段出行的最优路径相同，如图5所示，总出行时间为208 min。虽然所有出行者均能按其最优路径出行，选择城市轨道交通作为城际铁路两端的接驳方式，但实际在城市轨道交通服务时间窗以外的出行无法通过该路径实现。

图5 场景1的最优出行路径Fig.5 Optimal travel path under scenario 1

场景2 出行者时间价值较低

假设9 类出行者中有3 类具有较低时间价值，分别为20，50，80元·h-1，涵盖全天3个出行时间窗，即[7:00, 13:00]，[13:00, 19:00]，[16:00, 22:00]，出行时间预算均为6 h。则最优建设方案为修建路段(11,24)和(17,24)，实际投资710 亿元，能满足所有出行者在其期望时间窗内按最优路径出行，如图6所示。一共有6条时空轨迹描述这9类出行者的城际出行链。其中，时间价值为80元·h-1的出行者选择城际铁路(17,24)，在出发城市选择自驾车或打车前往城际铁路车站，路径总出行时间为188 min；其余出行者均选择城际铁路(11,24)，使用城市轨道交通作为城际铁路两端的集散方式，路径总出行时间为268 min。由于期望的出行时间窗不同，即便经由相同物理路径的出行者，也可能由不同车辆完成运输任务。

图6 时空网络中场景2的最优出行路径Fig.6 Optimal travel path under scenario 2 on a space-time network

若仅修建路段(11, 24)，则只对时间价值为80 元·h-1的出行者带来人均32.3 元的广义费用损失，投资额将减少450亿元。

场景3 出行者时间价值较高

假设9类出行者对时间敏感、对费用不敏感，具有3类较高的时间价值，分别为130，160，190元·h-1，涵盖全天3 个出行时间窗，即[11:00,15:00]，[14:00,18:00]，[20:00, 24:00]，出行时间预算缩减到4 h。则最优建设方案为修建路段(17, 24)，实际投资450 亿元，能满足所有出行者在其期望时间窗内按最优路径出行，如图7所示。出行者选择两条物理路径出行，其中4 类出行者选择路径1，在目的地城市选择城市轨道交通到达最终目的地，路径总出行时间为188 min；另5 类出行者选择路径2，在目的地城市选择自驾车或打车到达最终目的地，路径总出行时间为174 min。这是由于时间窗在20:00-24:00的出行者到达目的地城市后，城市轨道交通已经收班，只能选择道路交通到达最终目的地。对于时间价值为190 元·h-1的出行者来说，其最短路径即为使用道路交通作为城际铁路两端的接驳方式(详见图7)。

图7 时空网络中场景3的最优出行路径Fig.7 Optimal travel path under scenario 3 on a space-time network

可见，本文提出的考虑个体差异的城际铁路规划模型在不同出行特征条件下，得到的最优解不同。如果区域内出行者时间价值不高，仅需投资260 亿元即可满足大多数出行需求，城际铁路车站需要着重考虑公共交通接驳；若区域内出行者对时间非常敏感、对费用不敏感，且夜间出行较多，则城际铁路车站需要着重考虑出租车、自驾车的接驳，并适当调整公共交通服务时间。综上，本文提出的城际铁路规划方法可以得到更符合特定区域出行者需求、投资效益更佳的规划方案。

4 结论

随着大数据技术的不断发展，对城际客流需求的掌握也将更加精细化，为城际铁路规划提供了新的技术支持。在此背景下，本文提出基于个体出行链的城际铁路规划模型。在3种具有相同规模、不同需求特征的场景下，优化得到的最佳建设方案不同，对应投资额也有所差异。结果表明，该方法可根据区域发展实际情况，为城际铁路规划提供参考。后续研究将拓展到多OD对的客流需求，考虑时变的路段旅行时间和交通工具定员不同等更为复杂、更切实际的因素。