基于卡尔曼滤波的交叉口排队长度实时估计模型

蒋阳升，高宽，刘梦，王思琛，姚志洪*

(西南交通大学，a.交通运输与物流学院；b.综合交通大数据应用技术国家工程实验室；c.综合交通运输智能化国家地方联合工程实验室，成都610031)

0 引言

排队长度是计算信号交叉口车辆延误、停车次数、排放[1]及优化交通信号配时方案[2]的关键参数。在自适应信号控制系统中，均将实时的交通流量、交叉口转向比、排队长度等交通状态作为其输入参数[3]。而交叉口的实时排队长度作为自适应交通信号控制的主要输入参数之一，对信号控制系统的有效运行起着关键作用。因此，准确实时地估计排队长度尤其重要。

目前，对于排队长度估计已有广泛的研究，多数研究集中在固定探测器上，而固定检测系统存在易失效，安装、维护和运营成本高等问题。随着车联网技术(Connected Vehicle，CV)的发展，从车联网环境中可以实时获取车辆位置、速度、加速度等信息。因此，相关研究提出基于车联网数据的排队长度估计方法。如姚佼等[4]基于车辆轨迹数据分析车辆在队列内的排队位置，建立面向延误最小的排队长度估计模型。代磊磊等[5]采用自适应权重指数平滑法，基于估计的流量建立以排队论为基础的排队长度预测模型，在饱和交叉口排队长度预测上有较高精度。庄立坚等[6]基于低渗透率浮动车数据，利用队尾浮动车位置估计最大排队长度，该方法很大程度上依赖浮动车渗透率。王钰等[7]利用车辆GPS数据，建立基于交通波理论的交叉口排队长度估算模型，实现排队长度的估计。CHENG等[8]引入临界点提取算法，基于识别的轨迹数据临界点，提出基于改进冲击波理论的排队长度估计方法，实例分析表明，该方法可实现逐周期排队长度的估计。ZHAO 等[9]基于贝叶斯理论，根据网联车在交叉口停车位置分布估计排队长度，并通过仿真数据和实际数据验证模型的有效性。LI 等[10]建立基于数据融合的排队长度估计方法，分别构建了基于事件和冲击波理论的卡尔曼滤波排队估计方法，将两种方法的估计结果加权得到最终的排队长度。但分析结果表明，该数据融合方法有一定的局限性。此外，YIN等[11]提出使用低渗透率车联网数据的卡尔曼滤波排队长度估计方法。以上研究验证了卡尔曼滤波方法可以用于排队长度的估计。然而，现有基于卡尔曼滤波的排队长度估计方法仅讨论最大排队长度的估计，不能提供秒级的实时排队长度估计结果；而且这些方法都是基于历史轨迹数据，没有充分利用实时的车联网数据。

本文提出基于卡尔曼滤波的实时排队长度估计模型，根据交叉口的输入输出数据构建卡尔曼滤波的状态转移方程和观测方程，提出排队长度估计流程和性能评价指标，并基于实际数据构建仿真环境验证该模型的有效性。

1 标准卡尔曼滤波方法

标准卡尔曼滤波包括：状态转移方程和观测方程[12]。状态转移方程假设时间t的状态是从时间(t-1)的状态演变而来；观测方程可以根据时间t的估计状态和噪声来计算时间t的观察值(或测量值)，具体为

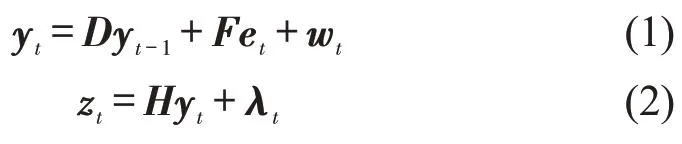
式中：yt为状态向量；D为状态转移矩阵；et为控制变量；F为控制输入矩阵；wt为状态随机变量，取值为均值为0的多元正态分布N，噪声协方差为Q，即w～N(0,Q)；t为时刻；zt为观测向量；H为观测矩阵；λt为取值于协方差为R的观察噪声，即λt～N(0,R)。

2 基于卡尔曼滤波的排队长度估计方法

为准确估计排队长度，本文假设在每个给定的时间间隔(例如：1，5，10 min)，可以通过感应线圈检测器或交通视频监控获得交叉口的车流转向比。此外，交通流量、渗透率和饱和流量等可以通过现有方法进行估计[9]。进而，基于这些数据构建基于卡尔曼滤波方法的秒级排队长度估计模型。

2.1 状态转移方程

根据式(1)，标准状态转移方程包含：当前状态，先前状态，状态转换矩阵，当前输入变量，控制输入矩阵，以及当前状态随机变量，分别表示为yt，yt-1，D，et，F和wt，这些变量在不同的动态系统中物理含义各不相同[13]。

在信号交叉口，当前状态为交叉口不同相位的排队车辆数。在时间t处的排队车辆数、t-1 处的排队车辆数和时间t处加入、离开排队队列的车辆数有关，如图1所示。

加入排队的车辆数由交叉口的车流到达率和转向比确定，离开排队的车辆数取决于信号灯状态和饱和流率。因此，状态转移方程表示为

式中：xi,t为时间t相位i的排队车辆数；qi,t为时间t相位i加入队列的车辆数；gi,t为时间t相位i的信号灯状态(1 或0)；si为相位i的饱和流率；P为相位集合，本文P={1,2,3,4,5,6,7,8} 。

标准交叉口信号相位如图2所示。

图1 信号交叉口的排队Fig.1 Queue at a signalized intersection approach

图2 标准交叉口信号相位Fig.2 Definition of a standard NEMA(National Electrical Manufactures Association)signal phase

对于标准四路交叉口，其状态转移方程的矩阵和向量形式为

式中：xt为时间t的排队长度状态向量，即

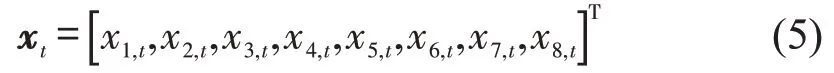
ut为时间t的输入变量，包含加入排队的车辆数qt和时间t的信号状态gt，即

A为状态转换矩阵，即

B为控制输入矩阵，即

2.2 观测方程

观测方程通过观测转换矩阵H最小化观测状态与从状态转移方程获得的估计状态之间的差距得到。在车联网环境中，如果渗透率为100%，则估计状态等于观测状态，表示观测矩阵为单位矩阵；对于渗透率不为100%的情况，利用排队网联车的数量和时间t相位i的渗透率获得。定义所观测的排队长度与实际排队长度之间的关系为

式中：ρi,t为时间t相位i的网联车渗透率；zi,t为网联车观测的排队车辆数，计算公式为

式中：pi,t为在时间t相位i排队的网联车数量，通过网联车的实时位置和速度获得。

因此，观测方程为

式中：zt为在时间t处观测的队列长度，即

若交叉口各个相位的渗透率不一样，则观测矩阵为

式中：矩阵对角线ρi(i=1,2,…,8)为各个相位的实际渗透率值。

通常，假设网联车在交通系统内某个区域的渗透率为定值[13]，故本文假设交叉口所有相位的渗透率相同，为ρ。因此，H表示为

2.3 噪声协方差

在式(1)和式(2)中，状态转移方程和观测方程的噪声协方差矩阵(Q和R)很难直接获得。HAO P.[14]开发的回归模型通过使用来自仿真实验的离线数据估计噪声协方差矩阵。本文采用该方法估计状态转移方程和观测方程的噪声协方差矩阵。

2.4 队列长度估计流程

获得以上参数后，卡尔曼滤波方法估计队列长度的流程如图3所示。

图3 通过卡尔曼方法估计排队长度的步骤Fig.3 Step of estimating queue length by Kalman method

图3中，Kt为在时间t处卡尔曼增益值；Φ*t为在时间t处的预测误差协方差；Φt为在时间t处观测更新后的误差协方差；为时间t处预测队列长度；x^t为时间t处观测更新后的队列长度；I为单位矩阵。

由图3可知，卡尔曼滤波方法估计队列长度包括两个步骤：时间状态更新和观测更新。具体地，在步骤1 中估计前一步状态和误差协方差；步骤2中计算卡尔曼增益，估计结果和误差协方差。

2.5 性能指标

本文模型的性能取决于估计与实际排队车辆数的差距。因此，为更好地评估模型性能，选择平均绝对误差(MAE)，平均绝对百分比误差(MAPE)和均方根误差(RMSE)作为评估标准。计算公式分别为

式中：li,t、分别为时间t相位i的实际、估计车辆数；T为总的离散时间；Li,n、分别为周期为n时相位i的实际、估计的最大排队车辆数；M为总周期数。

3 案例分析

选择成都市合适的交叉口收集数据，包括：交通量、限速、转向比和交叉口的几何形状，交叉口的位置和几何形状如图4所示。

图4 仿真实验交叉口Fig.4 Intersection of simulation experiment

每个进口道包括1 个左转车道和2 个直行车道，且交叉口处于非饱和状态。基于实际数据，在Vissim 中构建车联网仿真环境，验证模型的有效性。

3.1 仿真设置

3.2 仿真结果与分析

通过仿真实验数据，获得交叉口各个相位实际的排队长度数据；同时，采用本文模型对排队长度进行估计。当渗透率和交叉口饱和度分别为0.5 和0.6 时，交叉口相位2 的排队长度估计值与实际值的对比结果如图5所示。

图5 仿真实验的队列长度动态估计Fig.5 Dynamics of estimated queue length for simulation experiment

由图5可知，本文模型能够实现逐秒级的排队长度估计，且估计值与实际值基本重合。

为更好地评估本文模型性能，计算所有仿真实验结果的评价指标。不同随机种子仿真实验结果的MAE，MAPE和RMSE的平均值如表1所示。可知，随着渗透率的增加，模型的估计误差逐渐减小。当渗透率大于30%时，MAE 和RMSE 分别少于2 辆和3 辆；当渗透率为40%时，MAPE 小于17.5%；但当渗透率非常低，仅为10%时，MAPE 高达70%。结果表明，模型对渗透率要求较高(如大于30%)，在渗透率很低(如10%)时，模型的估计性能较差。不同渗透率的估计误差如图6所示。

表1 不同渗透率下的估计性能Table 1 Estimated performance under different penetration rates

由图6可知，随着渗透率增加，3个误差指标均逐渐减小；在渗透率达到20%时，3个误差指标均有明显的下降。图6(b)中当渗透率达到20%时，MAPE下降最为显著，表明至少需要40%的渗透率才能确保MAPE在20%以内，说明模型对渗透率有较高的要求。

为验证模型有效性，以LI等[10]提出的基于数据融合的排队长度估计方法为基准，当交叉口饱和度时，本文模型的改进百分比如图7所示。

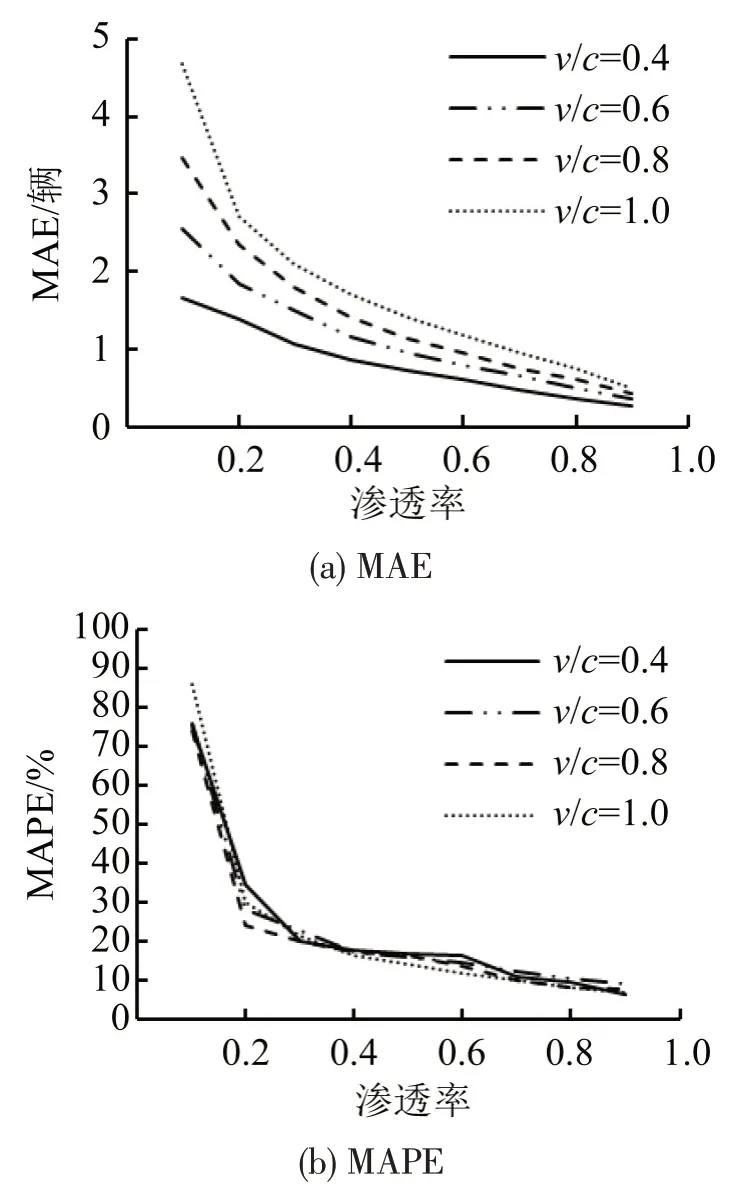
图6 不同渗透率下的估计误差Fig.6 Estimated errors under different penetration rates

由图7可知，当渗透率小于20%时，基准方法预测误差更小；而当渗透率大于20%时，本文方法的性能优于基准模型。表明本文模型和基准方法的应用条件不同，本文模型适用于较高渗透率的环境。特别地，当渗透率为90%时，与基准方法相比，本文模型MAE、MAPE 和RMSE 分别减少了10.5%、8.6%和9.8%，证明在高渗透率下本文模型能够获得较好的估计结果。

图7 模型的改进百分比Fig.7 Percentage improvement of proposed model

4 结论

本文提出卡尔曼滤波实时排队长度估计方法，利用实时网联车数据实现对交叉口排队长度的秒级估计。当渗透率为40%时，MAE、MAPE 和RMSE 分别小于1.5 辆、17.5%和2 辆。这表明该方法对渗透率有较高的要求。

与基准模型相比，当渗透率大于20%，本文模型对于排队长度估计结果误差较小，而在高渗透率下，本文模型估计的效果更优。但模型输入要求较高，后续研究可以考虑融合多源数据开发新的模型和算法减少本文模型对输入数据的高要求。