在习题教学中精准设问提升学生思维水平

文∣晏廷飞

《普通高中物理课程标准(2017年版2020修订)》从物理观念、科学思维、科学探究、科学态度与责任等四个方面提出了培养学生的核心素养。科学思维是物理核心素养的重要组成部分。发展科学思维本质就是提升学生的思维水平，提高学生思考辨析能力，提高学生分析、推理、质疑、判断、创新等能力。在习题教学中，可以在学生学习的关键之处、卡壳之处、易错之处设问，通过问题链，引导学生深入思考，不仅可以弥补学生知识缺陷，更能锻炼学生思维的严密性、灵活性、深刻性、敏捷性、批判性，从而实现学生思维水平的提升，实现核心素养的培养。

一、在容易遗漏条件之处设问，培养学生思维的严密性

思维的严密性要求思考问题时能够严格、准确，进行运算、推理时能够准确无误。思维的严密性对物理学科非常重要。但由于学生心理特点和认知水平等因素的影响，学生在物理学习过程中思维的严密性往往有所欠缺。学生在解决问题时，有时候会遗漏一些看似不重要的条件，因为没有这一条件，学生也能将问题解决，得到正确的结果。虽然看起来问题解决了，但是学生思考问题的逻辑存在严重的缺陷，只要将题目的条件稍作变化，学生马上就会掉入陷阱。教学中，教师有针对性地对这些遗漏条件设问，引起学生的重视，引导学生审视自己的解题过程，可以培养学生思维的严密性。

例1.在30 m高的楼顶以2 m/s的速度下抛物块，同时由静止释放小球.不计空气阻力，在下落2 s时物块与小球的距离是多少？(取g=10 m/s2)

(1)例1中其他条件都不变，在下落3 s时物块和小球的距离是多少？

(2)例1中将楼顶的高度改成22 m，问在下落2 s时物块和小球的距离是多少？

在问题(1)中物块和小球都已经落地，距离为零；在问题(2)中，物块已经落地而小球尚未落地，下落了20 m，二者的距离是2 m。通过这两问，一方面可以检验学生是否真的掌握了知识，另一方面培养了学生思维的严密性。

二、在能够拓展之处设问，培养学生思维的灵活性

思维的灵活性是学生思维品质的重要组成部分，思维灵活的学生能够活学活用，当遇到新的问题时往往能够自己独立思考出解决问题的新思路、好办法，能够将物理知识、物理思想方法迁移到新问题的解决中。物理教学中，要提升学生的思维品质就要培养学生思维的灵活性，当遇到一些可以拓展的教学内容时，引导学生从不同的侧面运用不同的物理知识、物理方法来思考问题、解决问题，可以培养学生思维的灵活性。

例2.在高速公路上行驶的汽车其速度为30 m/s，前方80 m处发生了交通事故，司机马上采取紧急制动，汽车经过4 s才能停下，汽车制动过程中加速度恒定。试分析该汽车是否有安全问题。

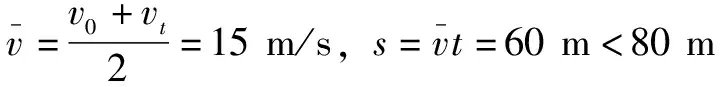
(1)描述物体运动的物理量有哪些？

(2)用位移这一物理量可以判断汽车是否安全，用别的物理量是否可以呢？请尝试别的解法。

通过问题引导与启迪，在师生的共同努力下找到多种解决问题的方法，拓展了学生解决问题的思路。引导学生从不同的角度思考问题，培养了学生思维的灵活性。

三、在易错之处设问，培养学生思维的深刻性

深刻性是思维的重要品质，要求能够全面、深入思考问题，要求能够透过表面现象洞察到事物的本质。学生在解决问题时觉得难，容易出错，其实只是在一两个易错之处学生没有想到，或者思考不透彻，这就是思维的深刻性不够。一道复杂的习题，往往只有一两个关键点，对学生的思维、能力要求较高。为此，在教学中教师只要抓住这一两个关键点进行设问，引导学生深入思考，将学生的思维引向纵深发展，让学生思考问题更深刻、透彻。

例3.图1是研究平抛物体运动实验用一张印有小方格纸记录的部分轨迹，小方格边长L=1.6 cm，a、b、c、d是小球平抛运动途中的几个位置。试求小球平抛的初速度v0=______(用L、g表示)，其值是______，小球在b点的速率为________。(取两位有效数字，取g=10 m/s2)

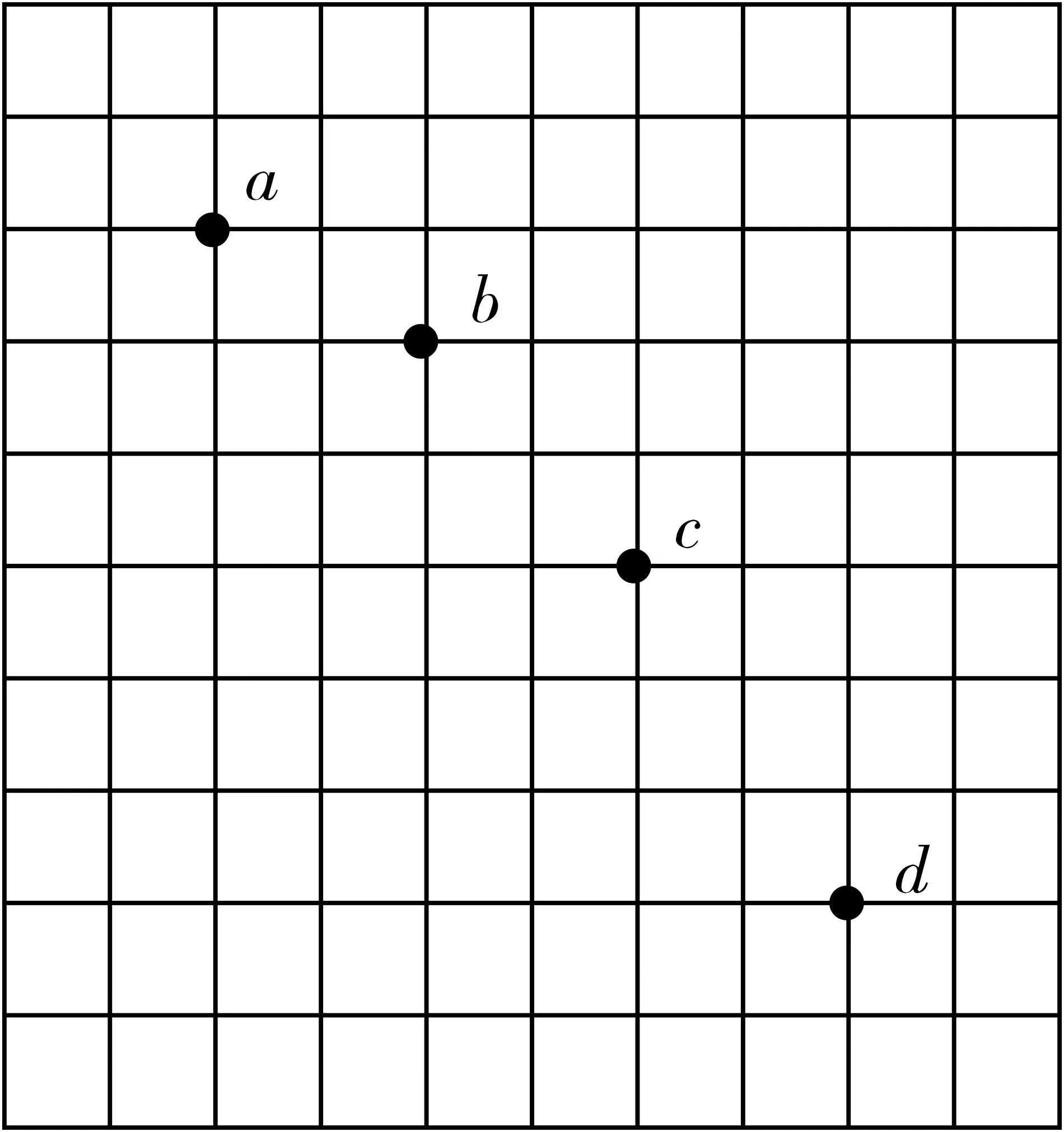
图1

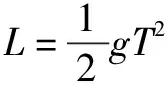
(1)a到b，b到c，c到d时间一样吗？你的依据是什么？

(2)a点是小球平抛运动的起点吗？

(3)如何判断a是不是平抛运动的起点？(如学生基础较差可将这一问改成：若a是平抛的起点，其竖直分位移有何特点？)

(4)小球在竖直方向的运动是匀变速直线运动，如何求解小球在b点的竖直分速度？

(5)如何求小球在b点的速度的大小？

通过上述问题的思考，问题的解决水到渠成(解答过程略)。教师通过引导学生思考，培养学生思维的深刻性。

通过上述计算可知a点不是平抛的起点，如果以a为原点，水平向右为x轴正向，竖直向下为y轴正向，建立坐标系，试求平抛起点的坐标。

上述问题针对学生错误的根本原因——误认为a点是平抛的起点，并在解决习题设置的问题之后，让学生求解平抛起点的位置坐标。设问针对学生“痛点”，有较强针对性。针对学生错误，引导学生深入思考，想透物理本质，理顺逻辑联系，有效培养了学生思维的深刻性。

四、在临界之处设问，培养学生思维的敏捷性

敏捷性反映了思维的速度和智力的敏锐程度。思维敏捷的人在思考和解决问题时能够根据情况的变化积极、周密地考虑，能够快速、准确地作出判断、得出结论。高中学习任务重，考试压力大，无论是平时的学习还是考试都要求学生在有限的时间内完成规定任务。这就要求学生解决问题不仅要追求准确，还要追求速度。故而，学生面对问题时，思维的敏捷性就显得很重要。只有思维敏捷才能够快速、准确想到解决问题的方法。

例4.如图2所示，质量m=5 kg滑块置于一粗糙斜面上，用平行于斜面大小为40 N的力F推滑块，若滑块沿斜面向上匀速运动，斜面体始终静止，取g=10 m/s2。求：(1)斜面对滑块的摩擦力大小；(2)斜面与滑块之间的动摩擦因素。

图2

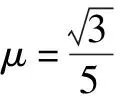
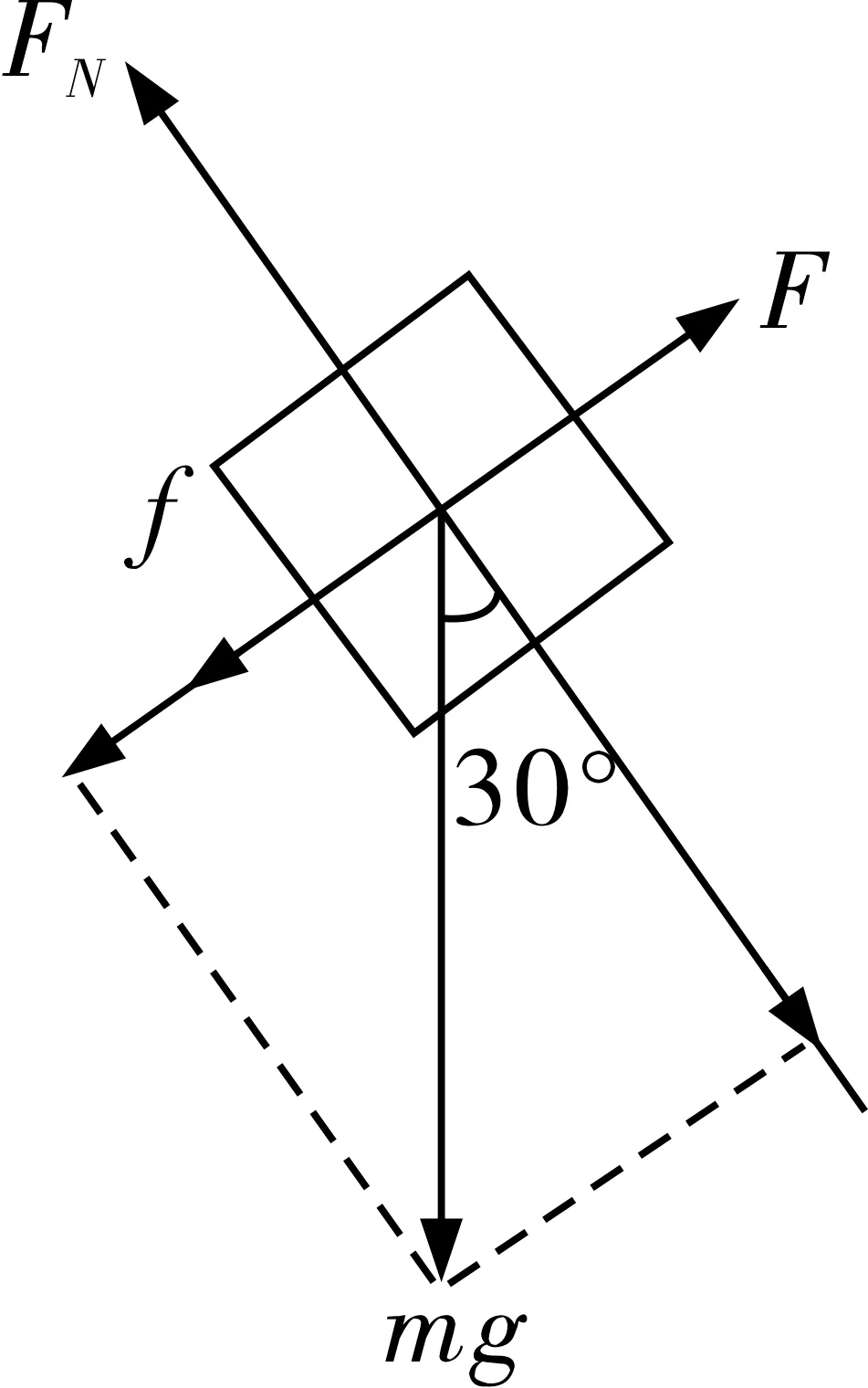
图3

物体在斜面上的情境，学生往往会想当然地认为有向上的力物体就一定会沿斜面向上运动。为此，可以假定最大静摩擦力等于滑动摩擦力，针对物体在斜面上能否滑动的临界提出以下问题：

(1)当推力F=30 N时，斜面对滑块的摩擦力为多大？

(2)若推力F=25 N时，斜面对滑块的摩擦力为多大？

(3)当推力F=10 N时，斜面对滑块的摩擦力为多大？

(4)当推力F=5 N时，斜面对滑块的摩擦力为多大？物体做什么运动？

(5)若要物体静止在斜面上则推力F的范围是多大？

通过问题引导，学生弄明白滑块恰好沿斜面上滑和恰好下滑时推力的临界值，找到这两个临界值，滑块能够静止在斜面上的条件就水到渠成。找到了临界值，有助于学生分析不同推力条件下滑块所处的状态或者运动情况，这有助于学生在今后解决问题时能快速寻找到解决问题的方向，提高解决问题的效率。

五、在思维定式之处设问，培养学生思维的批判性

批判性思维是合理、反思性的思维，是基于充分的理性和客观事实进行理论评估与客观评价的能力与意愿。具有批判性思维的人能够在与别人的交流中轻易发现别人的漏洞，并提出自己异于别人的见解。在教学中培养学生思维的批判性，有利于培育学生的创新意识和创新能力，没有批判就没有进步，就没有创新。学生在学习过程中，会因为生活经验、解题经验而产生思维定式。思维定式有时会对学生构建新知识产生不利影响。针对学生的思维定式设问，不仅可以破除学生的思维定式，还可以培养学生的批判意识，教会学生批判的方法，从而培养学生的批判思维。

例5.一小球以初速度v0=3 m/s水平抛出，经过一段时间后小球速度变为v=5 m/s，则这段时间内小球速度的变化是多少？小球下落的时间是多少？

由于学生从小开始接触的都是标量的运算，虽然在必修一学习了力的合成与分解，了解了矢量的运算。但是由于思维定式，学生依然不能熟练掌握矢量的运算方法。面对上述问题时，不少学生依然套用标量的运算法则，得到小球速度变化为2 m/s的错误结论。由于思维定式，学生没有作矢量图的意识，想不到构建如图4所示的矢量三角形。为此，可针对学生思维定式依次设问如下：

图4

(1)速度是标量还是矢量？

(2)矢量、标量的运算法则一样吗？

(3)你学过的矢量的运算有哪些？按照什么法则进行？

(4)在力的合成与分解时，3 N和4 N的合力一定是7 N吗？若不是，它们的合力可能是多少？

(5)5减3一定等于2吗？

(6)在这里5减3等于多少？为什么？

通过层层设问，让学生逐渐清晰，物体的速度和所受的合外力都是矢量，再合成与分解时，遵从与标量运算不一样的平行四边形定则和矢量三角形法则。从而破除学生思维定式，“破”的过程就是学生反思的过程，是学生进行批判思维的过程。

习题教学是提高高中物理教学效果的关键“最后一公里”，也是在课堂上落实核心素养培养的重要、关键阵地。抓好习题教学对帮助学生查漏补缺、提高思维水平、发展科学思维、落实核心素养培养至关重要。在习题教学中精准设问，可以引导学生逐步深入思考，由浅入深层层剥离问题，逐步触及问题本质，更重要的是可以很好地发展学生思维的严密性、灵活性、深刻性、敏捷性、批判性，从而提升学生科学思维水平。