高中数学直观想象能力培养策略探寻

郭龙祥

[摘  要] 数学研究的对象是数与形，数与形不是截然分开的，“形”可以用“数”来描述，“数”可以展示“形”的特征. 因此，要想真正实现数形结合，就必须为学生寻找到一个坚实的基础，这个基础体现在素养方面的直观想象素养. 直观想象包括两点，即几何直观与空间想象. 毫无疑问，直观想象的直接研究对象是“形”，而“数”则是作为研究“形”的工具而存在. 几何直观可以理解为空间想象的基础，空间想象可以理解为几何直观的思维延伸. 学生的直观想象能力要想得到有效的培养，关键要做两个工作：一是让学生有一个有效的数学模型，这个模型越清晰，学生的几何直观就越清晰，这个模型所包含的关系越丰富，学生的几何直观也就能够伸出更多的触角;二是学生要有足够的推理能力与想象能力，只有这样才能将新的问题情境中的信息与原有的模型产生联系.

[关键词] 高中数学;核心素养;直观想象

在高中数学学科核心素养的组成要素当中，直观想象是六个要素之一，在教学中必须想方设法予以落实. 从核心素养培育的角度来看，直观想象素养是指借助几何直观和空间想象感知事物的形态与变化，利用空间形式特别是图形，理解和解决数学问题的素养. 其主要包括：借助空间认识事物的位置关系、形态变化与运动规律;利用图形描述、分析数学问题;建立数与形的联系，构建数学问题的直观模型，探索解决问题的思路. 有时候对直观想象还有更为通俗的理解，也就是认为直观想象是几何直观与空间想象的结合. 这样的理解也是有道理的，数学研究的对象是数与形，数与形又不是截然分开的，除了人们熟知的数形结合之外，每个高中数学教师也都知道：“形”可以用“数”来描述，“数”可以展示“形”的特征. 因此，要想真正实现数形结合，就必须为学生寻找到一个坚实的基础，这个基础体现在素养方面就是直观想象素养. 本文试就直观想象素养，谈一谈笔者的一些实践基础上的认识，以及相关的思考.

■核心素养视角下的直观想象理解

要培养学生的直观想象素养，教师首先要对直观想象有深刻的理解，只有建立了科学的理解，才能用正确的理念引导生成正确的教学行为. 既然直观想象已经成为数学学科核心素养的要素之一，那么在核心素养的视角之下理解直观想象，也就成为高中数学教师的必然选择. 从上面的通俗理解来看，直观想象包括两点，即几何直观与空间想象. 毫无疑问，直观想象的直接研究对象是“形”，而“数”则是作为研究“形”的工具而存在.

同时直观想象还存在着一种依存关系：几何直观更多的是描述学生看到几何图形之后产生的直观感觉，而空间想象则是在几何直观的基础上，学生通过想象建构起来的新的结果（图形）. 因此，几何直观可以理解为空间想象的基础，空间想象可以理解为几何直观的思维延伸. 所以，培养学生的直观想象素养，就要搞清楚这种逻辑关系，也只有搞清楚这种逻辑关系，才能认识到直观想象有利于促进学生的知识与能力的形成，有利于提高学生分析和解决问题的能力，从而养成良好的数学思维习惯、创新意识以及应用数学意识与欣赏数学之美. 例如，在高中立体几何的知识体系当中，正方体是一个基本的图形. 作为立体几何中最为规则的图形，正方体是空间中点、线、面的结合，是一个基本的数学模型，也是培养学生几何直观的一个基础性模型. 这种模型在促进学生思维提升的方面有着重要的作用.

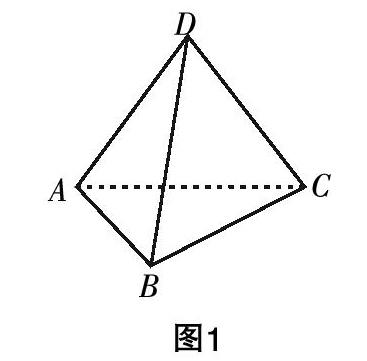
举一个例子，要让学生求一个正四面体（如图1）外接球的表面积和体积，学生会感觉比较困难，因为要确定球心的位置与球的半径，是比较难以寻找突破口的.

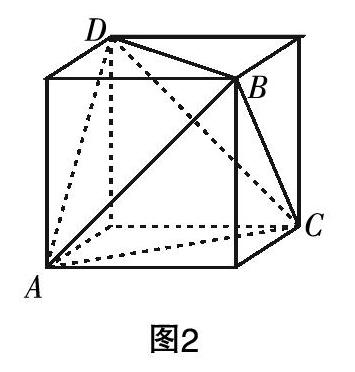
更加深入的分析表明，学生之所以难以突破，是因为大脑当中缺乏必要的几何模型. 如果学生大脑中的正方体模型比较清晰，那就可以将正四面体还原到正方体当中（如图2）. 这样的一个还原，就是几何直观的结果，只要学生大脑当中有清晰的正方体模型，并且以此直观作为基础进行想象，那么正四面体自然就会出现在正方体当中，从而为问题解决开辟新的视角.

■基于核心素养培养直观想象能力

从以上分析可以发现，直观想象能力确实支撑着学生的问题解决能力，这无论是从应试的角度来看，还是从核心素养培育的角度来看，都有着非常重要的价值. 对此有相关的研究表明，从“数学史与数学教育”（HPM）的视角去设计和实践不失为一种好的培养学生直观想象能力的选择，尤其是借鉴古代数学家的思想与智慧，应用“图说一体”“几何模型”和“经典反例”等实例来提高学生从直观想象到推理论证和理解的能力，以逐渐培养学生的直观想象素养. 来看一个课例：一道高考题的问题解决.

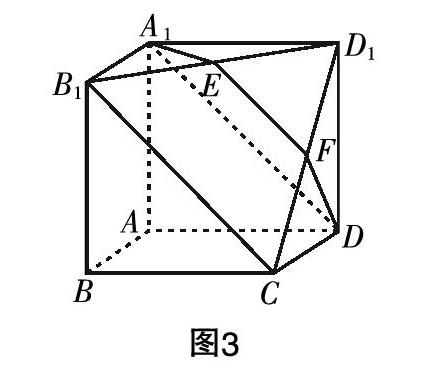
如图3，在多面体A■B■D■-DCBA中，四边形AA■B■B，ADD■A■，ABCD都是正方形，E是B■D■的中点. 现有一过A■，D，E的平面交CD■于F点.

（1）证明：EF∥B■C;

（2）求二面角E-A■D-B■的余弦值.

实际教学中当学生看到的是一个多面体时，立即会感觉到难度的存在，再加上是一个立体图形，学生的空间想象能力如果跟不上，那么这道问题的解决就会遇到非常大的挑战.

所以在解决这个问题的时候，笔者首先想到的是帮助学生进一步巩固一个模型，这个模型就是上面提到的正方体模型. 绝大多数情况下，学生大脑中所储存的正方体模型，就只是一个形体的存在，对其中的规律或者说关系并不十分清晰. 因此，教师教学的第一个任务就是帮学生丰富这个模型. 对此笔者的做法是：在幻灯片上继续呈现一个正方体，明确最基本的关系，如各边相等，等等. 其后，研究正方体的对角线（包括体对角线与面对角线，要把相应的线画出来），然后寻求关系，如面对角线跟体对角线垂直，体对角线（如图4中的BD■）被相应的面（如图4中的AC■D■）分为1∶2的两段，等等.

这样一个教学过程，虽然与解题并不直接相关，但是却丰富了学生对正方体这个模型的认识，客观上也就为学生的几何直观奠定了更为丰厚的基础. 在此基础上引导学生去想象——想象的方向就是这个基本图形与要解决的问题中的图形的关系. 学生通过对比可以发现，如果把原题中的多面体补全了，补成一个正方体，那就可以得到一些基本的关系，而通过这些基本关系的运用，就可以实现问题的求解. 由于这个过程与直观想象能力的培养距离较远，因此这里就不再占用篇幅赘述.

回到直觀想象能力培养这个主题上来，在上面的课例当中可以发现，学生的直观想象能力要想得到有效的培养，关键要做两个工作：一是让学生有一个有效的数学模型，这个模型越清晰，学生的几何直观就越清晰;这个模型所包含的关系越丰富，学生的几何直观也就能够伸出更多的触角. 二是学生要有足够的推理能力与想象能力，只有这样才能将新的问题情境中的信息与原有的模型产生联系. 而从核心素养培育的角度来看，这种基于较为完整的、清晰的几何直观模型的合理想象，就应当是学生在数学学习中表现出来的关键能力，也因此培养学生的直观想象能力的过程，就是培养学生数学学科核心素养的过程.

■直观想象培养不是一个孤立过程

大量的课例分析可以积累大量的教学经验，而大量的教学经验表明，直观想象的培养其实并不是一个孤立的过程，很大程度上可以将其理解为一个系统工程. 初步的研究表明，在直观想象的培养过程中，学生需要进一步借助几何直观来发展空间想象能力，增强用图和识图的能力，体会空间几何特征的刻画方法和刻画的本质，培养创新思维. 进一步的研究发现，当把直观想象解析为几何直观与空间想象之后，直观想象能力培养的逻辑也就变得很清楚了，也就是上面所强调的，在几何直观的基础上培养学生的空间想象能力. 之所以说这是一个系统工程，是因为在巩固学生的几何直观基础的时候，教师也有大量的工作要做. 在上面的课例当中可以发现，几何直观常常需要模型作为支撑，于是这就涉及数学学科核心素养中的数学建模;空间想象需要学生进行有逻辑的推理与想象，于是这又涉及逻辑推理，其中还有可能涉及运算，等等. 因此，一个直观想象将数学学科核心素养中的多个要素组织在一起，从而形成一种系统的学习形态. 因此，在培养学生直观想象能力的时候，教师一定要有系统思维，绝对不能将直观想象孤立起来，否则那样的教学过程，一定不能让学生的直观想象素养真正落地.