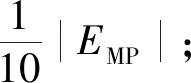用于量值传递的高精度单晶硅球质量测量研究
彭 程,王 健
(中国计量科学研究院,北京 100029)
1 引 言
第26届国际计量大会(Conférence Générale des Poids et Mesures,CGPM)通过的关于“修订国际单位制(SI)”决议于2019年5月20日正式生效。新定义后的量值传递体系发生了变化,为使新定义后的质量单位在现有的质量传递系统中得到落实,其复现和传递工作十分关键。目前的研究主要聚焦于1 kg标称质量值的复现与传递,其中对于千克质量值的复现主要有2种相互独立基准方法:一是通过利用约瑟夫森电压和量子化霍尔电阻导出量子电功率基准,再进一步导出质量基准的电学天平方案来复现得到一定质量的实物基准,称为“瓦特天平”方案[1]。由于采用该方法时需要对多个电学相关参量进行测量,目前电学天平系统设计较为复杂,测量装置庞大且成本高昂。另一种是通过对高纯度单晶硅中的硅原子进行计数,利用一定质量纯度极高的单晶硅球内硅原子数目来建立量子质量基准的X射线晶体密度法(X-ray crystal density,XRCD)[2,3]。从实际应用上考虑,无论采用瓦特天平方法或X射线晶体密度法,均需要将基于物理常数定义的质量值复现在一定质量的实物载体之上,以用于向后继续传递至各级砝码。随着半导体产业中大型单晶硅生长技术的成熟发展,高化学纯度和无位错的单晶硅材料易于获得,单晶硅球被用作新定义后质量复现和传递工作中最为理想的实物基准[4]。通过X射线晶体密度法方法复现得到的质量主基准为高纯度单晶硅球,质量副基准通过在真空中与主基准校准后继续向下传递至具体应用场所,硅球质量测量将成为未来量值传递工作中的重要一环。不仅如此,在密度测量领域中单晶硅球是现行国家密度实物基准,单晶硅球的绝对密度测量必须对硅球质量进行准确测量[5]。因此,对高精度单晶硅球的质量测量相关技术和方法的研究具有重要意义。
由于硅球与现行圆柱体型或OIML型等标准砝码的材质属性及几何特性存在较大差异,且空气浮力修正主要由被测砝码与参考砝码的体积差值与空气密度的乘积计算得出,由于硅球与常用砝码体积差值扩大,测量环境中空气密度变化带来影响更加显著,为确保量值传递的准确性,硅球质量修正值计算需要在过去的修正方法上加以改进。因此,本文研究了美国国家标准与技术研究院(NIST)、中国计量科学院研究院(NIM)以及OIML-R111国际建议中对于开展不同精度的质量测量时环境参数变化范围的要求[6~8],采用CIPM-2007公式法计算分析不同环境参数变化对空气密度测定的影响;对实际测量过程中的密度变化情况分析得出在单个测量序列内存在6种不同的变化序列,基于质量测量原理提出将单次测量序列中实验室环境的空气密度实时测量值代入空气浮力修正值计算,并通过数值模拟分析忽略空气密度瞬态变化对硅球质量测量带来的空气浮力修正计算误差。
2 硅球质量测量原理
ms=mref+Δm
(1)
式中Δm为硅球质量修正值。通过对质量修正值Δm的来源进行分析得出,在潮湿空气中测量时,质量修正值主要产生于硅球与参考砝码之间体积及表面性质上存在的较大差异,使得二者所受空气浮力大小、重心位置及表面水分子吸附力不同[9,10]。在进行质量修正时,应分别考虑各部分对硅球质量测量的影响,硅球质量测量的质量修正值Δm计算公式为:
(2)

我国最高国家质量基准为铂铱合金砝码,合金密度约为21 500 kg/m3[11],质量副基准采用JF1无磁不锈钢材料,其密度约为8 000 kg/m3。单晶硅球与现行使用的各级砝码物理性质之间存在着明显差异[12],根据各质量基准材料属性及几何外形差异,表1为不同材质的1 kg质量基准主要物理性质。

表1 不同材质1 kg质量基准的性质Tab.1 1 kg mass standard in different materials
在实际测量过程中,参考砝码与被测物体的体积差异导致二者所受的空气浮力大小不同,在进行测量过程中需要进行空气浮力修正[13]。1 kg铂铱合金砝码与1 kg不锈钢材质砝码其体积差值约为80.5 cm3;由于单晶硅材质密度较小,1 kg硅球与 1 kg 铂铱合金砝码之间的体积差值约380 cm3。若考虑测量时的空气密度为1.2 mg/cm3,采用1 kg铂铱合金砝码作为参考砝码,1 kg不锈钢砝码进行质量测量时空气浮力修正值约为96.6 mg,1 kg硅球空气浮力修正值可达到459.6 mg。现行各级砝码形状主要为圆柱体或OIML型,与相同质量下单晶硅球重心高度差异明显,在精确测量中应考虑重心高度的修正。地面重心高度差的修正因子约为0.3 μg/mm[13],1 kg铂铱合金砝码与1 kg单晶硅球重心高度差修正值可达6.69 μg。新定义后质量基准的复现过程在真空条件下进行,副基准进行量值传递时需从真空条件下取出时,空气中的潮湿水分子会附着于表面使得质量值增加[14]。Picard A[10]等在先前的研究中通过重力法测得单晶硅材料表面水蒸气吸附修正因子为30 ng/cm2,其标准不确定度为9 ng/cm2,根据表1中数据可知,1 kg硅球置于潮湿空气中表面水蒸气吸附量约为8.3 μg,标准不确定度为2.5 μg。2012年,日本国家计量院(NMIJ)利用吸附块法间接测定硅球表面水蒸气物理吸附量为12.0 μg,相对不确定度为4.7 μg[15,16]。硅球质量测量修正值的近似计算结果如表2所示。
由表2可知,其质量修正的主要来源是测量环境下所受空气浮力不同带来的影响。空气浮力修正值通过计算测量时的空气密度及被测物体与参考砝码之间体积差值的乘积得到,固体密度经测量后短时间不会发生明显改变,而测量时环境条件波动变化使得空气密度难以达到绝对恒定,实际测量过程中空气密度存在一定程度的漂移。由于单晶硅球与其它材质砝码之间体积差值较大,使得在高精度测量中空气密度的细微变化也会对空气浮力修正带来显著影响。本文进一步对空气密度瞬态变化进行分析,并对NIST,NIM及NMIJ进行检定校准时普遍采用的空气浮力计算方法加以改进,提出考虑瞬态空气密度的空气浮力修正算法,以提高在硅球质量测量时的空气浮力修正准确度。

表2 1 kg硅球质量测量修正值计算Tab.2 Mass correction of 1 kg silicon spheres
3 空气浮力修正计算方式的改进
3.1 测量环境条件变化对空气密度的影响
质量测量采用的衡量仪器主要为基于电磁力反馈平衡原理的高分辨率质量比较仪,其工作原理为通过多组循环测量,以整个测量序列的单次测量结果标准偏差来得出质量差值。为减少线性漂移对衡量结果的影响。以ABA(A1B1A2)循环模式为例,在该循环测量模式下AiBiAi+1三次交替组合称量过程作为单次测量序列,i为放置在衡量盘上的砝码顺序号,i=1,2,…,n。
当测量示值序列为IA1,IB1,IA2,IB2,IA3,…,IAn+1时,单次测量的质量差值结果计算公式如下[11]:
图4为不同压下量的Cockcroft-Latham损伤结果,对比3个不同压下量下结果可以发现,在试样鼓肚及附近位置出现明显损伤,特别是鼓肚位置的损伤值较大,而坯料上下端未见明显损伤。随着压下量的增加,鼓肚位置的损伤值不断增加。分析其原因,是由于在鼓肚位置由于没有约束,处于自由变形状态,在正的应力三轴度的作用下,此处的损伤将不断增加。当达到材料的临界损伤值时,试样中将出现明显的裂纹。
(3)
式中A和B为2个具有相同标称值的砝码。
为了对测量时的空气密度进行测定,在日常检定中目前主要采用CIPM-2007公式法,通过质量比较仪内的温度、湿度、大气压强及二氧化碳浓度传感器接收实时环境参数测量对测量环境空气密度进行数值计算。由于在实际测量过程中,质量比较仪进行多组循环测量时单个测量序列测量中包含的3次交替称量持续时间约为5~8 min,即使是对温度湿度场进行严格控制的恒温恒湿实验室或计量检定室,其测量环境条件也难以保持恒定不变,每次称量时,通过环境参数测定的空气密度值浮动变化将对测量结果的准确性造成一定影响。因此,各国国家计量技术机构对于各准确度等级砝码检定时的环境条件变化状况提出了相应的要求。NIST提出对于高精度等级质量测量中,在1组测量序列中温度变化量应低于0.5 ℃,且全年内,温度变化应在±1 ℃/24 h,对于较低等级的砝码检定校准中(如Echelon Ⅱ等级)规定温度应在18~23 ℃范围内,且允许的最大变化量为±2 ℃/12 h及1.5 ℃/1 h,相对湿度应在40%~60%范围内,且4 h内变化量应低于±10%。我国砝码检定规程中对环境参数变化的规定等同采用OIML-R111国际建议,对于高精度等级砝码(如E1,E2等级砝码)规定检定时每4 h的温度最大变化0.5~1 ℃,空气的相对湿度最大变化5%~10%。为了分析环境参数变化对空气密度测定的影响,本文基于CIPM-2007空气密度计算公式定量分析测量时的温度、湿度在不同程度波动变化下对测量环境的空气密度计算值的影响,分析结果如表3所示。从空气密度变化量计算结果可知,在进行高精度等级的测量时,温度和湿度在规定允许的范围内波动时,通过CIPM-2007公式法测定的空气密度将随之产生10-3~10-4kg/m3的变化。

表3 环境参数变化对空气密度测定的影响Tab.3 Influence of environmental conditions fluctuations on air density estimation
为了进一步研究在实际测量中环境参数变化对空气密度测算的影响,本文收集了在恒温恒湿实验室进行质量测量时,质量比较仪封闭腔体内的空气密度实时数据,记录每次称量时的空气密度所得到的空气密度变化曲线如图1所示。

图1 恒温恒湿实验室空气密度变化曲线Fig.1 Air fluctuation curve in laboratory with temperature and humidity under well-controlled condition
图1中的空气密度变化曲线反映了1组采用ABA循环测量模式的质量测量在12 h内,共计273次空气密度采集结果,由于实验室对温度和湿度恒定控制,测量过程中实验室环境温度控制在(20±0.1) ℃,相对湿度控制在52.1%~52.3%,实验过程中的大气压强变化范围为1 014.36~1 014.11 hPa,二氧化碳摩尔分数变化范围为784.7~830.5。结合图1可知,测量过程中空气密度整体上变化趋势具有一定的稳定性,测量结果分布在1.200 7 kg/m3到1.201 0 kg/m3范围内,由于环境参数如二氧化碳浓度、大气压强、温度和湿度等产生浮动变化,在测量过程中空气密度值呈现随机性波动,根据变化曲线可知任意一组测量序列中相邻两次测量的空气密度若产生浮动变化,其变化幅度约为1×10-4kg/m3。根据实际测量过程中的密度变化曲线进行分析,可以得出若设定测量时环境空气密度大致稳定于ρa,相邻2次测量的空气密度变化量为δ时进行,在包含3次称量过程的单个测量序列中,空气密度变化呈现出如图2所示的6种变化序列(Ⅰ,Ⅱ,…,Ⅵ),其中Ai1Bi1Ai2(i=1,2,3,…,n)表示ABA循环模式下的第i个测量序列,其中A作为参考砝码需要在被测砝码测量前后分别进行一次测量。
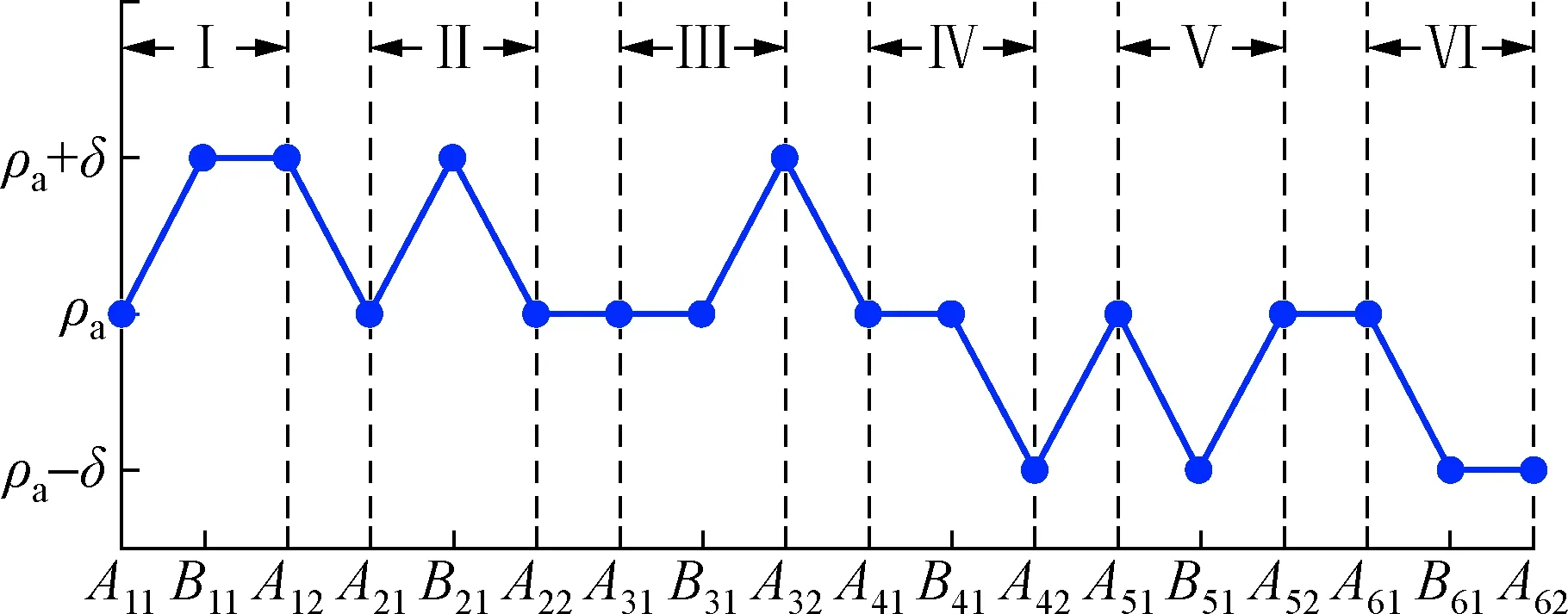
图2 单个测量序列中的空气密度变化序列Fig.2 Air fluctuation series in one ABA weighing cycle
由于从铂铱合金砝码传递到不锈钢材质砝码,或在同种材质砝码之间传递过程中参考砝码和被测砝码间体积差值较小,交替称量中的空气密度变化带来的影响不会造成各级量值传递或校准工作中要求的测量精度损失从而可忽略不计,因此各国国家计量检定机构在日常检定工作中,空气密度常取多次循环测量序列中的均值,取空气密度恒定值带入计算空气浮力修正。若考虑未来采用单晶硅球进行量值传递,由于其与现有砝码体积差值的显著扩大,在空气浮力作用下空气密度的瞬态变化亦将对质量测量结果产生重要影响,在精确测量中不容忽视。本文基于对硅球质量测量的研究,提出一种考虑空气密度瞬态变化的空气浮力计算方法,引入空气密度的实时测量结果计算硅球质量测量的空气浮力修正。
3.2 硅球质量测量的空气浮力修正优化算法
依据JJG 99-2006《砝码检定规程》进行空气浮力修正时,空气密度通常取恒定值进行计算,在ABA循环测量模式下包含3次交替称量过程的单次测量序列中,对硅球进行质量测量时空气浮力修正计算采用式(4):
Δmb1=ρa×(Vs-Vref)
(4)
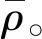
根据3.1节中分析可知,在实际的质量测量过程中存在单个测量序列中存在密度瞬态变化,使得每次称量时的空气密度存在一定差异,仅考虑空气浮力对质量测量的影响,由质量比较仪得到的示值应为:
I=m-ρaV
(5)
式中:m为物体质量;V为该物体的体积。
采用ABA测量模式对硅球进行测量,由此得到3次称量测得的示值序列I1,I2,I3:
(6)
式中:m1,m2,m3分别为3次称量的质量值;ρ1,ρ2,ρ3分别为3次称量时的空气密度。
结合式(3)中给出的单次测量质量差值计算式可知,若考虑测量过程中空气密度存在3次称量过程中的空气浮力修正值合成为:
(7)
式中Δmb2为具体考虑3次称量过程中密度变化后得到的空气浮力修正值。
3.3 2种不同空气浮力修正方式的差异分析
基于是否考虑单次测量中空气密度发生的细微变化,3.2节中给出了2种空气浮力修正的计算方式,为了分析引入空气密度浮动变化计算空气浮力修正结果与空气密度取恒定值计算2种方式之间的差异:
(8)
根据式(8)给出的差值计算式,取定硅球质量测量环境空气密度大致稳定于1.2 kg/m3,且相邻2次测量间的空气密度变化量取3.2节中恒温恒压实验室实际测量数据的变化量1×10-4kg/m3,按照表1中给出的不同材质物理性质,分析1 kg铂铱合金砝码作为参考砝码进行1 kg单晶硅球质量测量时,采用2种不同空气浮力修正方式带来的计算差异。基于式(8)进行计算的具体结果在表4中给出,由表4可知在测量过程中空气密度大致稳定于1.2 kg/m3时,由于空气密度存在瞬时变化,单个测量序列的3次称量时的空气密度可能产生浮动,当测量序列内的3次空气密度值的变化以图2所示的6种空气密度变化序列形式存在时,若仍采用空气密度取单一值进行空气浮力修正将产生约为15.1~30.2 μg的计算误差;其中3次测量时空气密度若以I、Ⅲ、Ⅳ、Ⅵ类变化序列存在时,计算误差的绝对值为15.1 μg,若产生Ⅱ、V类型变化时,产生的误差绝对值约为其他类型的2倍;根据上述分析表明由于显著体积差值的存在,对硅球质量进行测量时如果忽视单次测量过程中的密度瞬态变化情况,将对空气浮力修正的准确性带来较大影响。
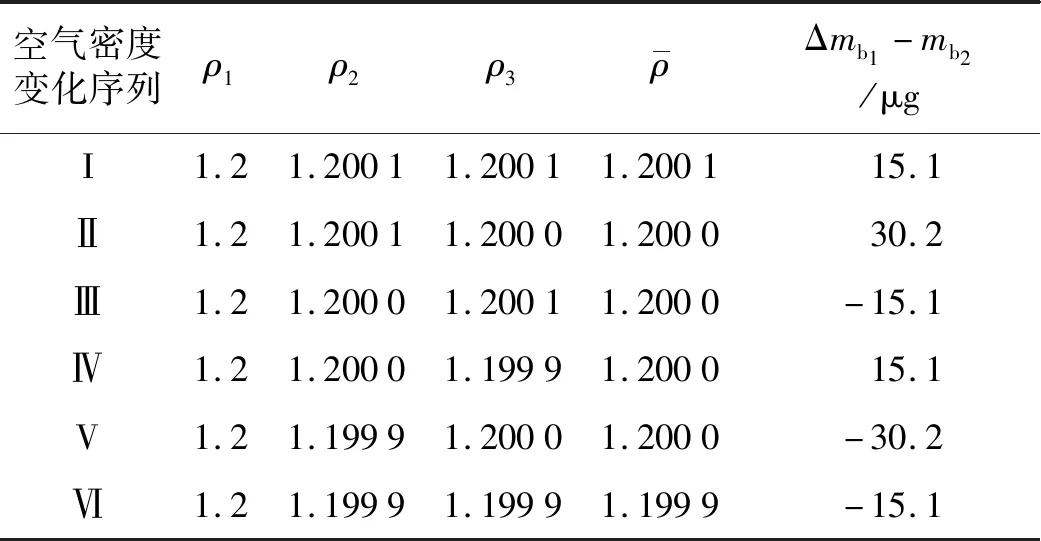
表4 2种不同空气浮力修正方式计算差异Tab.4 Differences of two methods in air buoyancy correction mg·cm-3
若采用硅球作为质量基准将质量值传递至各级砝码时,由于目前常用砝码材料的密度主要分布在8 000 kg/m3左右,铂铱合金砝码密度相对更大,约为21 400 kg/m3;而天然单晶硅球的固体密度相对较小,对于1 kg标称质量,相同质量的天然单晶硅球与其他材质砝码之间的体积差值约为288~380 cm3。为了研究硅球作为质量基准与其他材质砝码开展测量时,空气密度的浮动变化对测量结果的影响,本文结合3.1节中的环境条件变化范围,对空气密度浮动取极限变化量即0.000 1~0.005 0 kg/m3,待测砝码按照砝码检定规程中列出的常用砝码类型,以图2中的空气密度变化序列I为例进行空气浮力修正的数值模拟,计算得出若忽略测量过程的空气密度浮动变化将带来的空气浮力修正误差值,结果如表5所示。
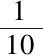

表5 不同材质砝码的空气浮力修正误差值Tab.5 Errors of air buoyancy correction in weights manufactured in different materials μg
4 结 论
本文基于对硅球质量测量的研究,对硅球质量测量原理进行分析,提出对硅球质量修正值计算模型,并对作为质量修正主要来源的空气浮力修正计算进行深入研究,对测量过程中的空气密度瞬态变化带来的修正误差进行分析。研究结果表明:
1) 在对硅球质量测量结果进行质量修正时,根据其物理特性,应进一步考虑由空气浮力、潮湿空气中水分子吸附及重心高度差带来的影响,经计算分析后可知,由于单晶硅材质密度较小,以1 kg铂铱合金砝码为参考砝码进行质量测量时,1 kg硅球的空气浮力修正值可达到459.6 mg,空气浮力修正为硅球质量修正值的主要来源。
2) 由于在测量过程中环境参数的动态变化,测量时的空气密度仍难以避免地发生着细微改变,通过对大量采集的数据进行分析,发现测量过程中空气密度整体上大致稳定于某一范围,但在单个测量序列的3次交替称量过程中,空气密度值会绕某一稳定值出现瞬态随机波动,根据本文实时采集的空气密度测量结果梳理得出,质量测量过程中单个测量序列内空气密度的浮动存在着6种不同的变化序列,各变化序列将对空气浮力修正的结果产生不同的影响。