基于峰谷互补方法的开关磁阻电机转矩脉动抑制研究

何伟福,王宁黎,赵 浩,冯 浩

(1.杭州电子科技大学，浙江 杭州 310018;2.嘉兴学院，浙江 嘉兴 314001)

1 引 言

开关磁阻电机(switched reluctance motor,SRM)具有结构简单、可靠性高、调速性能好等优点,在汽车、矿山、纺织等多个领域得到了广泛应用。但SRM的双凸极结构和非线性磁路,以及脉冲工作方式,使SRM运行时存在明显的转矩脉动,限制了SRM的推广应用。国内外学者对SRM的转矩脉动及其抑制方法做了大量研究,提出的解决方法主要分为2种:一种是从电机本体设计入手,如文献[1～3]通过优化定、转子结构,减小边缘磁通影响,从而降低转矩脉动;另一种是从控制策略入手,如文献[4]介绍了一种分段谐波电流控制策略,采用向初始矩形参考电流中注入多次谐波分量,使之生成相应的额外转矩,来补充或消除原参考电流产生的转矩脉动。文献[5]提出了一种磁链与电流自适应补偿的TSF优化方案,得到恒转矩下较理想的参考电流波形,间接达到减小转矩脉动的目的。文献[6]通过设计转矩滞环控制器,使得转矩能实时跟随给定转矩,以此减小转矩脉动。转矩分配控制策略也是现今转矩脉动抑制的一个热门方向[7],文献[8]从本身电机实际尺寸出发,利用模型仿真得到不同转子位置和相电流下的转矩,建立了转矩-电流逆模型,文献[9,10]分别以铜耗、电流变化率以及相电压需求最小化为目标优化了转矩分配策略。这些方法在一定程度上降低了转矩脉动,但抑制效果不甚理想。

本文在理论分析SRM转矩脉动产生原因和实际测量转矩脉动波形的基础上,提出了一种基于峰谷互补叠加抵消转矩脉动的方法:两套电磁参数相同的开关磁阻电机工作在相同工况,脉动转矩波形相位互差180°,转矩叠加后输出驱动负载。

2 开关磁阻电机数学模型

SRM的运行遵循“磁阻最小原理”,即磁通总会沿着磁阻最小的路径闭合。通过控制SRM定子各相绕组的顺序产生磁场,转子会向磁阻最小的位置转动的趋向,产生连续转矩使电机运转。为简化分析,通常采用线性模型分析电机工作的基本特性和各参数间的相互关系。

各定子绕组电压方程为:

(1)

式中:i为绕组相电流;R为绕组相电阻;θ为转子位置角度；Ψ(i,θ)为相绕组磁链。

由于SRM各相绕组间的互感相对于自感而言甚很小,可忽略不计,这时绕组磁链可近似成相电流与自感及转子位移角θ的关系函数:

Ψ=Ψ(i,θ)=L(i,θ)·i

(2)

式中L(i,θ)为相电感。将式(2)代入式(1),得定子绕组电压方程为:

(3)

式(3)表明,L、Ψ和u都随着θ变化,体现了SRM磁路的非线性。

由于SRM磁路的非线性,通常SRM的转矩根据磁共能来计算,由一相产生的转矩通式为:

(4)

式中:Te为其中一相产生的瞬时转矩;W为相绕组磁共能。

显然,磁共能的改变既取决于转子位置,也取决于绕组电流的瞬时值。在磁路饱和状态下运行的SRM是一种非线性严重的机电装置,磁共能很难解析计算。

线性模型时式(4)可简化为:

(5)

SRM总的瞬时转矩为各相瞬时转矩之和,本文所用的SRM是三相6/4极电机,故总瞬时转矩为:

(6)

根据力学定律可列出电机转子机械运动方程为:

(7)

式中:TL为负载转矩;J为转动惯量;F为阻尼系数;ω为角速度;dω/dt为旋转角加速度。

转矩脉动的产生原因主要有2个:其一,由于磁链为非线性函数,即使通入恒定的电流,瞬时相转矩也不是一个恒定的值,必定会存在转矩脉动。其二,由于电机绕组视为感性负载,因此换相时绕组相电流以一定速率上升或下降,即梯形电流波形,进一步产生脉动转矩。本文以分析当导通角为120°时电机换相的相电流波形为例,如图1所示。其中Off_A,On_B,On_C,Off_B分别为A相绕组关断,B相绕组开通,C相绕组开通,B相绕组关断。

图1 SRM换相时电流变化图Fig.1 Current Change Diagram in SRM Commutation

由图1可知,SRM在换相区域,当前关断相电流下降速率与下一开通相电流上升速率不等时,换相时段的合成电流将产生相对脉动。通过选择不同的开通与关断角度值,可以优化相电流的实时波形,但由于电机参数的非线性和不对称性,换相区域的合成电流相对脉动依然存在进而产生脉动转矩。

3 SRM转矩脉动仿真与实验

3.1 转矩脉动仿真

文献[11～13]对分别在电流斩波控制(CCC)、电压斩波控制(CVC)和角度位置控制(APC)方式下的电磁转矩与三相电流进行了仿真,分别如图2～图4所示,仿真结果可知,以换相为主频的振动转矩确实是存在的。

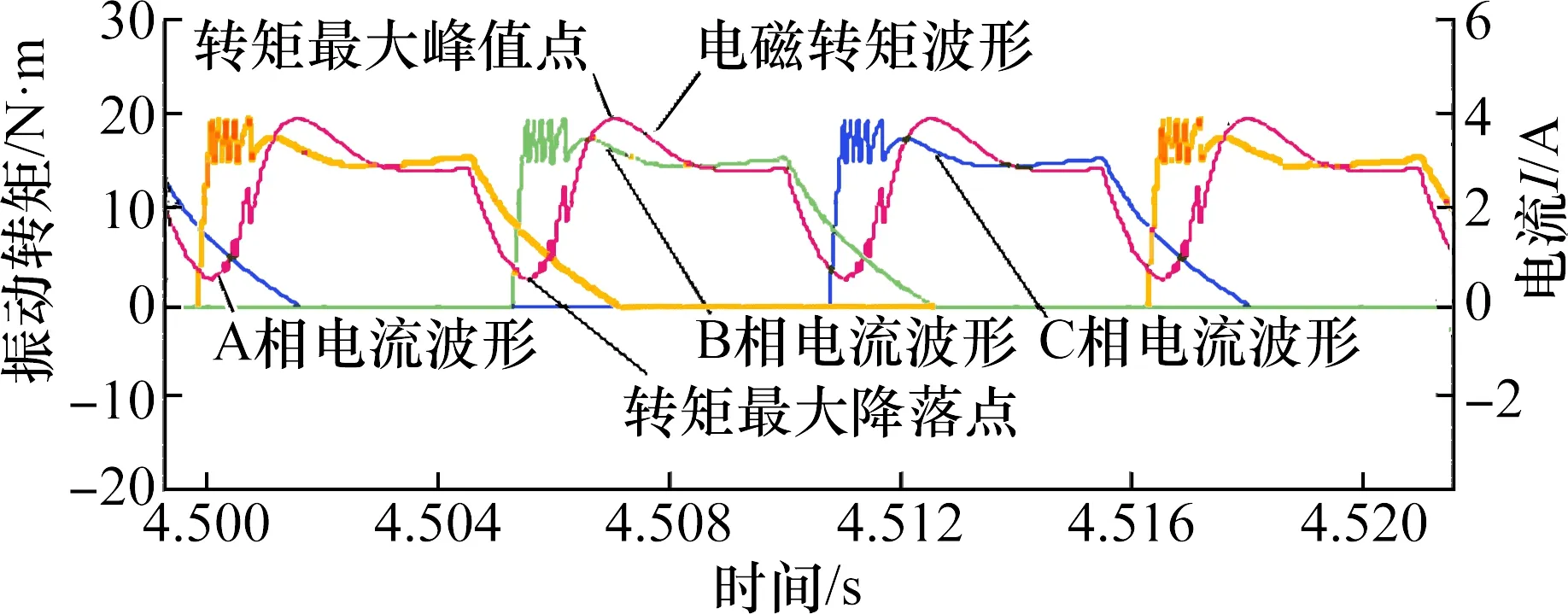
图2 CCC方式电磁转矩与相电流的仿真波形Fig.2 Simulated waveforms of electromagnetic torque and phase current in CCC mode

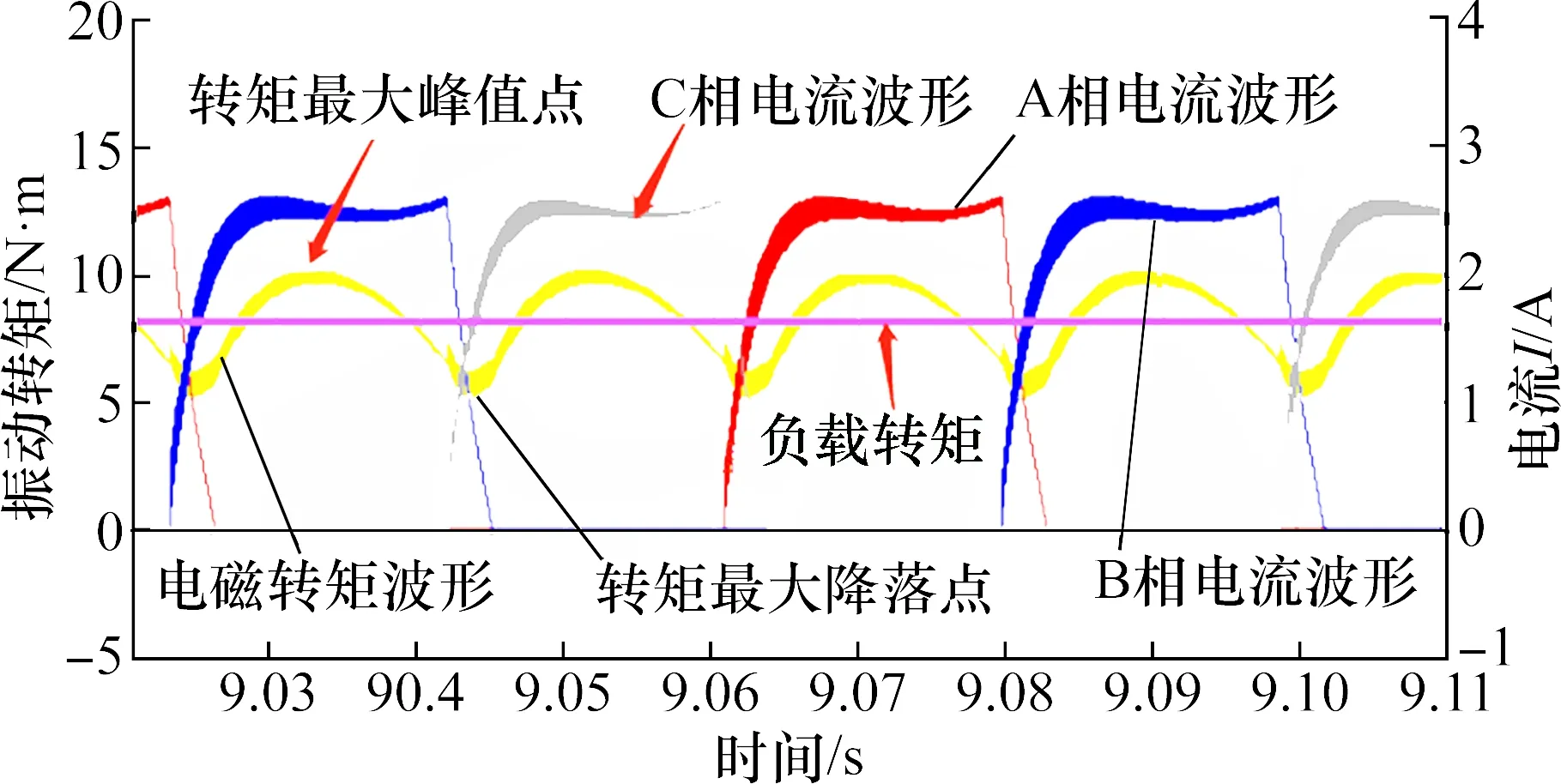
图3 CVC方式电磁转矩与三相相电流的仿真波形Fig.3 Simulation Waveform of Electromagnetic Torque and Three Phase Current in CVC Mode

图4 APC方式电磁转矩与三相相电流仿真波形Fig.4 Simulated waveforms of electromagnetic torque and three-phase current in APC mode

3.2 转矩脉动测量实验

当SRM带载运行后,阻尼系数很小可忽略不计,由式(7)可得简化后电机的转矩平衡方程:

(8)

由式(8)可知,当SRM存在转矩脉动时,会以转轴旋转角加速度的形式表现出来,可以通过测量SRM轴上的旋转角加速度及系统的转动惯量来间接测量SRM轴端的转矩脉动。

构建的实验测量系统如图5所示,包括开关磁阻电机及控制器、机械负载、旋转角加速度传感器和数字示波器,对应测试平台实物如图6所示。

图5 实验测量系统框图Fig.5 Experimental measurement system block diagram

图6 实验测量平台实物图Fig.6 Physical Chart of the Measuring Platform

实验测试了单台开关磁阻电机在不同转速下的旋转角加速度(即开关磁阻电机的脉动转矩)的大小,图7和图8是实验(SRM-60 V-200 W)开关磁阻电机在340 r/min振动转矩波形图和振动转矩的频谱分析图,图9和图10为实验开关磁阻电机在 370 r/min时测得转矩脉动波形和对应该运行速度下的转矩脉动波形的频谱分析图。

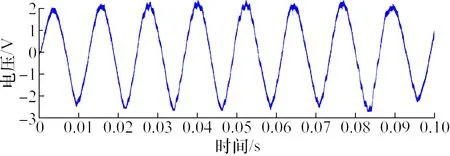
图7 转速为340 r/min转矩脉动波形图Fig.7 Torque ripple waveform of 340 r/min

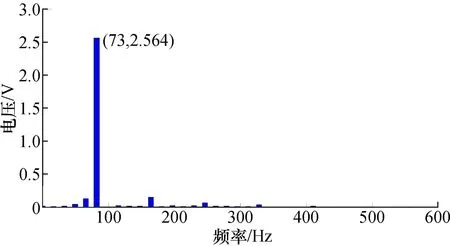
图8 转速为340 r/min转矩脉动频谱分析图Fig.8 Spectrum Analysis of Torque Ripple at 340 r/min

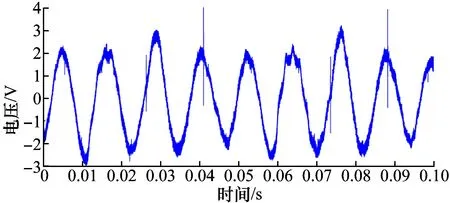
图9 转速为370 r/min转矩脉动波形图Fig.9 Torque ripple waveform of 370 r/min

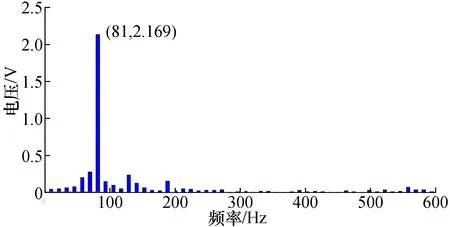
图10 转速为370 r/min转矩脉动频谱分析图Fig.10 Spectrum Analysis of Torque Ripple at 370 r/min

由测量结果可知:开关磁阻电机在换相过程中产生的转矩脉动是客观存在的,当电机转速n为340 r/min时,对应的转速频率为n/60=5.67 Hz,6/4极开关磁阻电机步距角为30°,转一圈需要换相12次,因此由换相引起的转矩脉动频率应为SRM电机转速频率12倍频,即为68 Hz;同理,电机转速为370 r/min时,电机转速频率约为6.16 Hz,由换相引起的转矩脉动频率为74 Hz。

从频谱的角度分析,图8中幅值最高点出现在73 Hz,在当前状态开关磁阻电机转速频率68 Hz附近;图10中幅值最高点出现在81 Hz也在转速频率74 Hz的附近。造成转矩脉动基波频谱与理论值不相同的原因主要是:开关磁阻电机定、转子齿的空间分布存在误差,导致步距角不均匀;绕组电流换相过程中存在误差。

4 开关磁阻电机转矩脉动抑制

4.1 基于峰谷互补的转矩脉动抑制方法

由第3节实验结果可知,SRM电磁转矩的最大降落和最大转矩脉动呈周期性出现,且电磁转矩的峰值脉宽和谷值脉宽以及振幅也近似对称。因此,选用2台同样参数的开关磁阻电机,将它们各自产生的转矩脉动错开180°电角度,从基本的物理概念可知,可以有效抑制SRM的转矩脉动。

实验中的SRM电机为三相6/4极,转子旋转一周相电流有12次换相,会引起12个周期的转矩脉动。因此,将2套原来对齐的转子凸极位置错开15°空间机械角,即可实现左右两套电机系统产生的换相转矩脉动对应的电角度互差180°,能够保证转矩脉动得到最大抑制。转矩脉动峰谷互补方法的原理如图11所示。图11中#1、#2表示不同的2条转矩波形曲线。

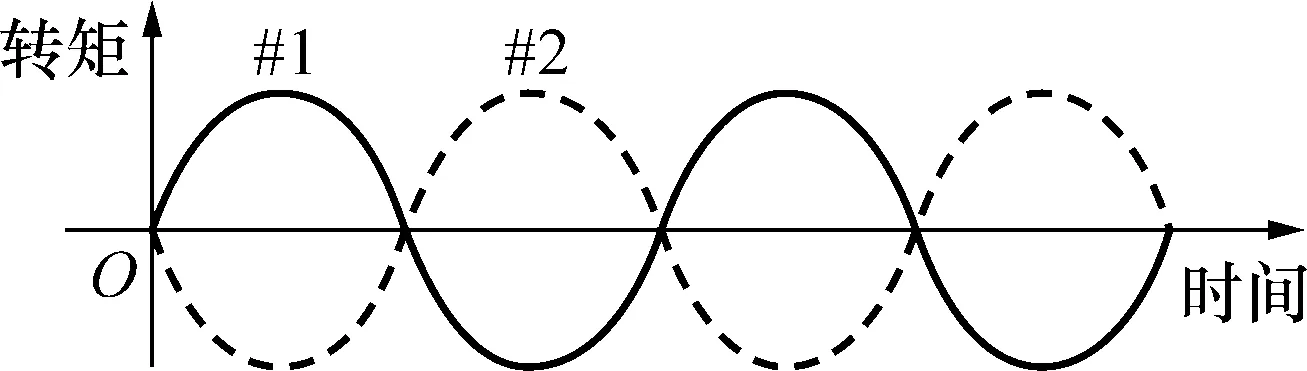
图11 峰谷互补原理Fig.11 Peak-valley complementary schematic diagram

4.2 转矩脉动抑制实验平台

根据本文提出的方法,设计如图12所示的实验系统,对应的实物如图13所示。

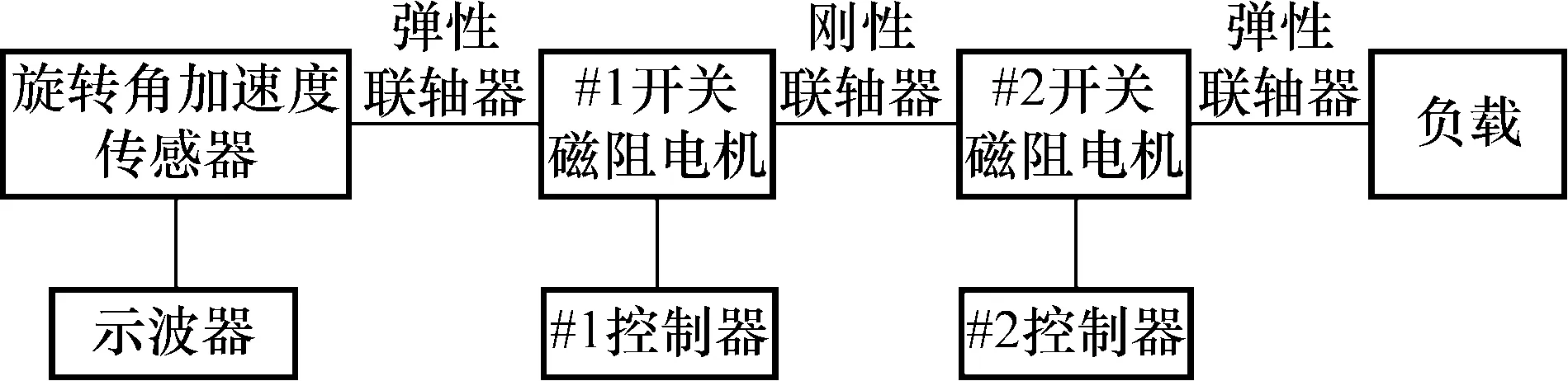
图12 实验系统框图Fig.12 Block diagram of experimental system

图13 实验系统实物图Fig.13 Physical Chart of Experimental System

在SRM实际运行中,要实现本文提出的抑制SRM转矩脉动方法的关键是:当2台电机转轴同心同轴相联后,要尽量保证2台电机分担相同的输出功率,即要保证2台电机都工作在相同的机械特性工作点下。

图13的实验系统中,通过磁粉制动器施加一定的负载,2台电机的母线电压给的都是32V,先启动#1号电机,将电机的稳态转速调至为340 r/min;此时关掉#1号电机,再启动#2号电机并将稳态转速调至340 r/min,并且此时2台电机的母线电流几乎相等;再同时启动2台电机,并且通过增大磁粉制动器的励磁电流慢慢增大负载转矩,直到同轴相连的2台电机的转速都达到340 r/min,此时仍要确保2台电机控制器的母线电流相等(实际实验中是近似相等2台电机有0.05 A微小误差),如果母线电流明显不同,则仅需要微调其中一个电机的控制器就可以使之相同,由此实现2台电机的同工作点、同功率运行。

4.3 转矩脉动实验结果与分析

在340 r/min和370 r/min转速下,2台SRM电机转子位置对齐时,转矩脉动的波形分别如图14和图15所示,对应的频谱分别如图16和图17;2台SRM电机转子位置在空间错开15°机械角时,转矩脉动的波形分别如图18和图19所示,对应的频谱分别如图20和图21所示。

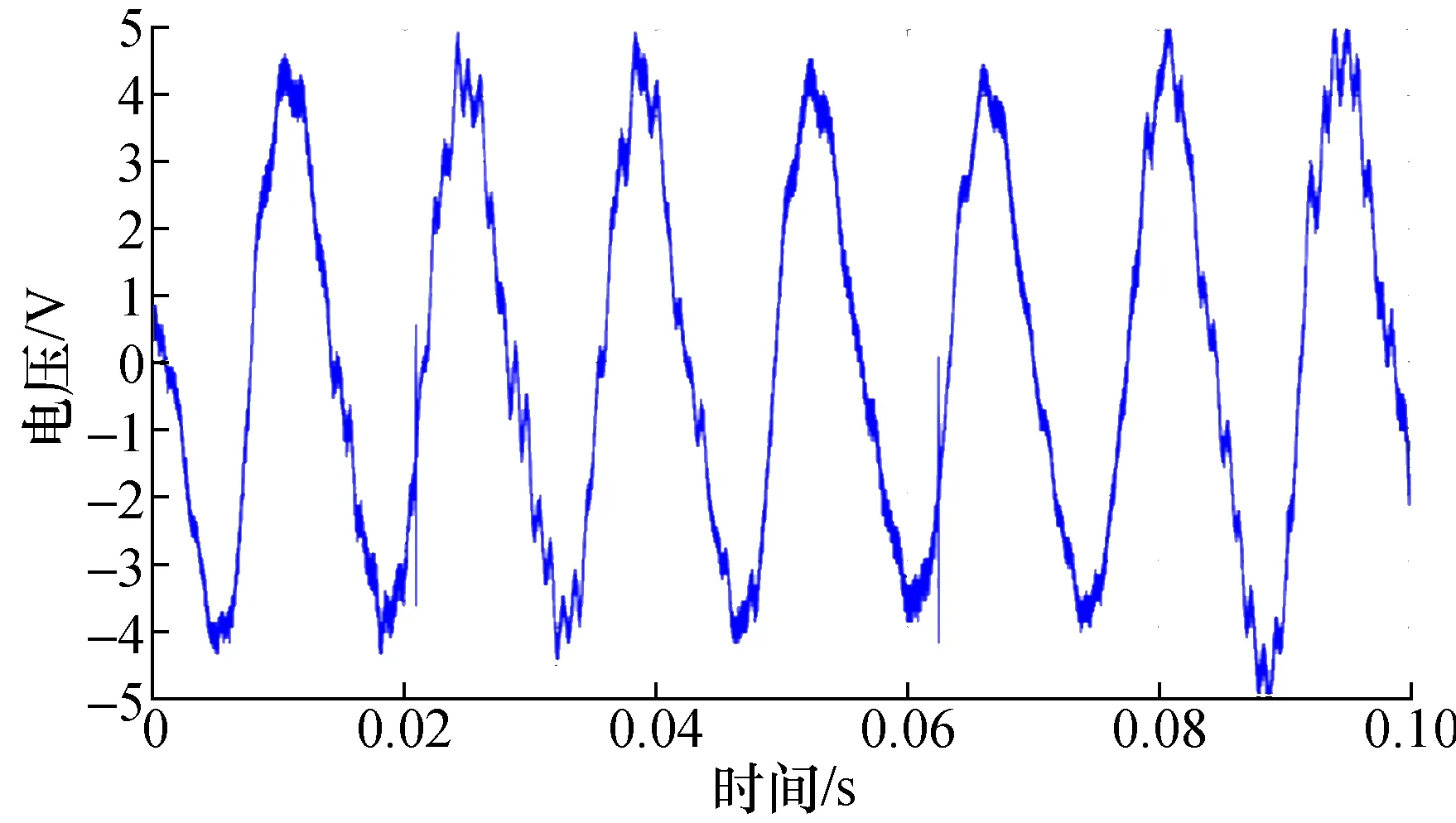
图14 转子对齐时340 r/min转矩脉动波形图Fig.14 Torque ripple waveform on 340 r/min

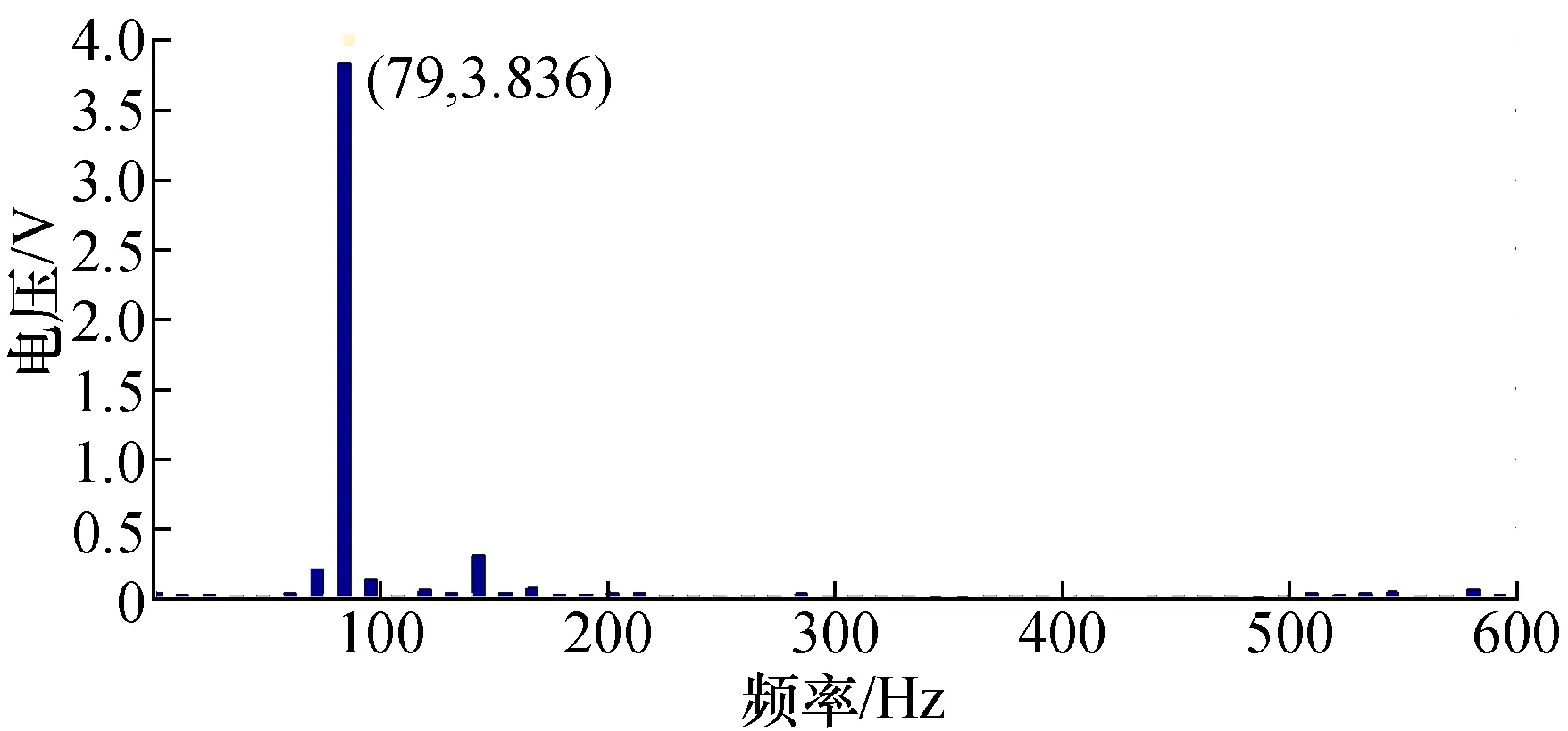
图15 图14对应的频谱分析图Fig.15 Spectrum analysis of 340 r/min torque ripple waveform

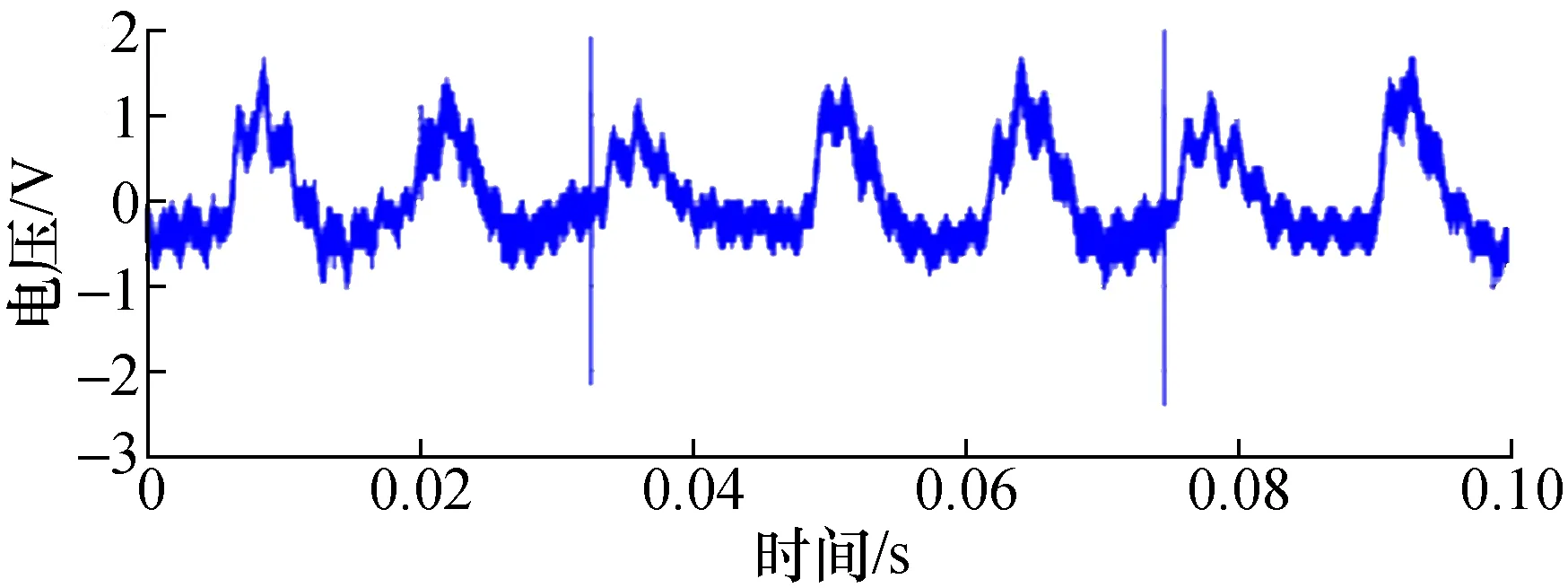
图16 340 r/min抑制后转矩脉动波形图Fig.16 Torque ripple suppression waveform on 340 r/min

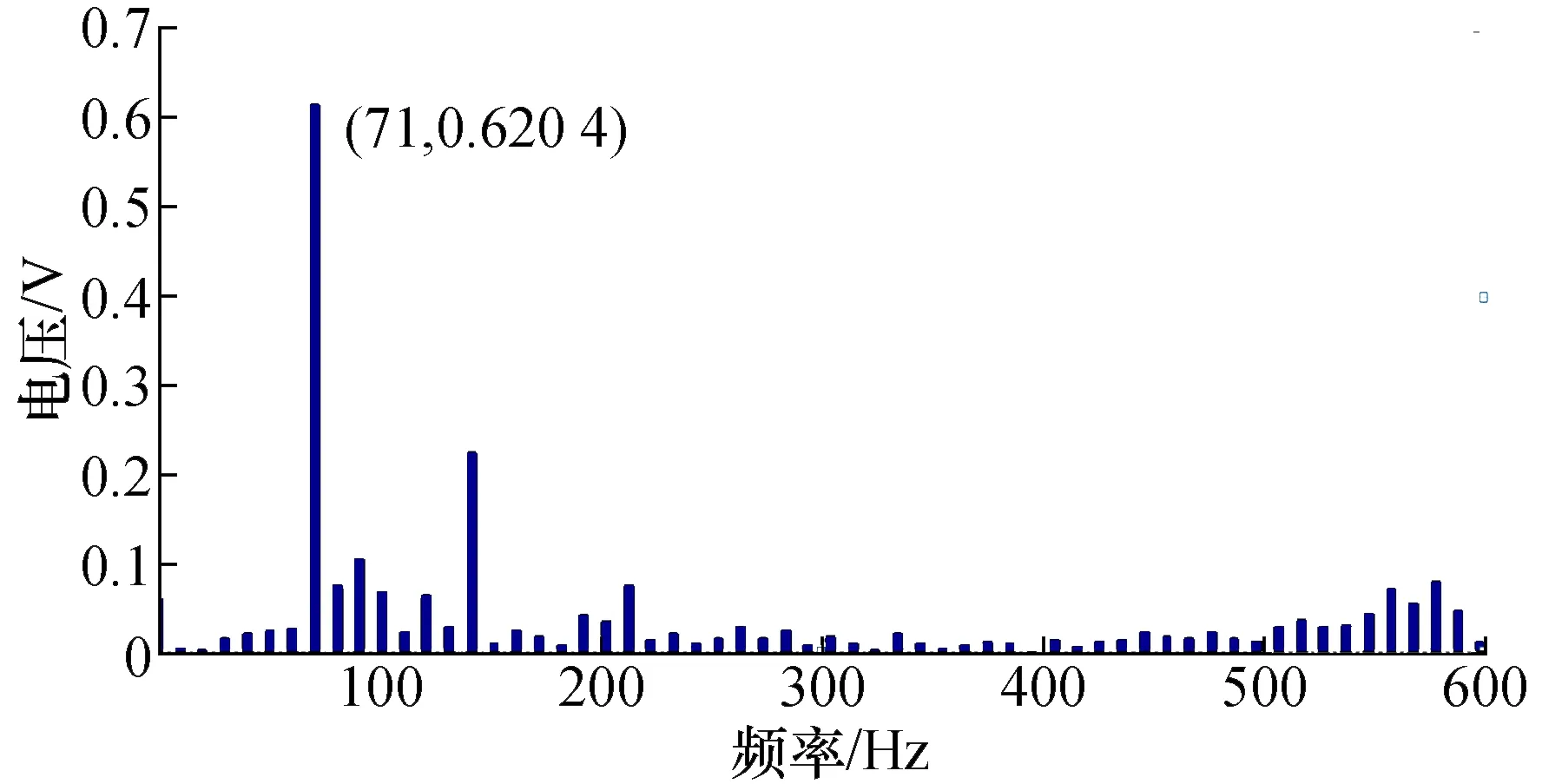
图17 340 r/min抑制后转矩脉动波形频谱分析图Fig.17 Spectrum analysis of torque ripple suppression waveform on 340 r/min

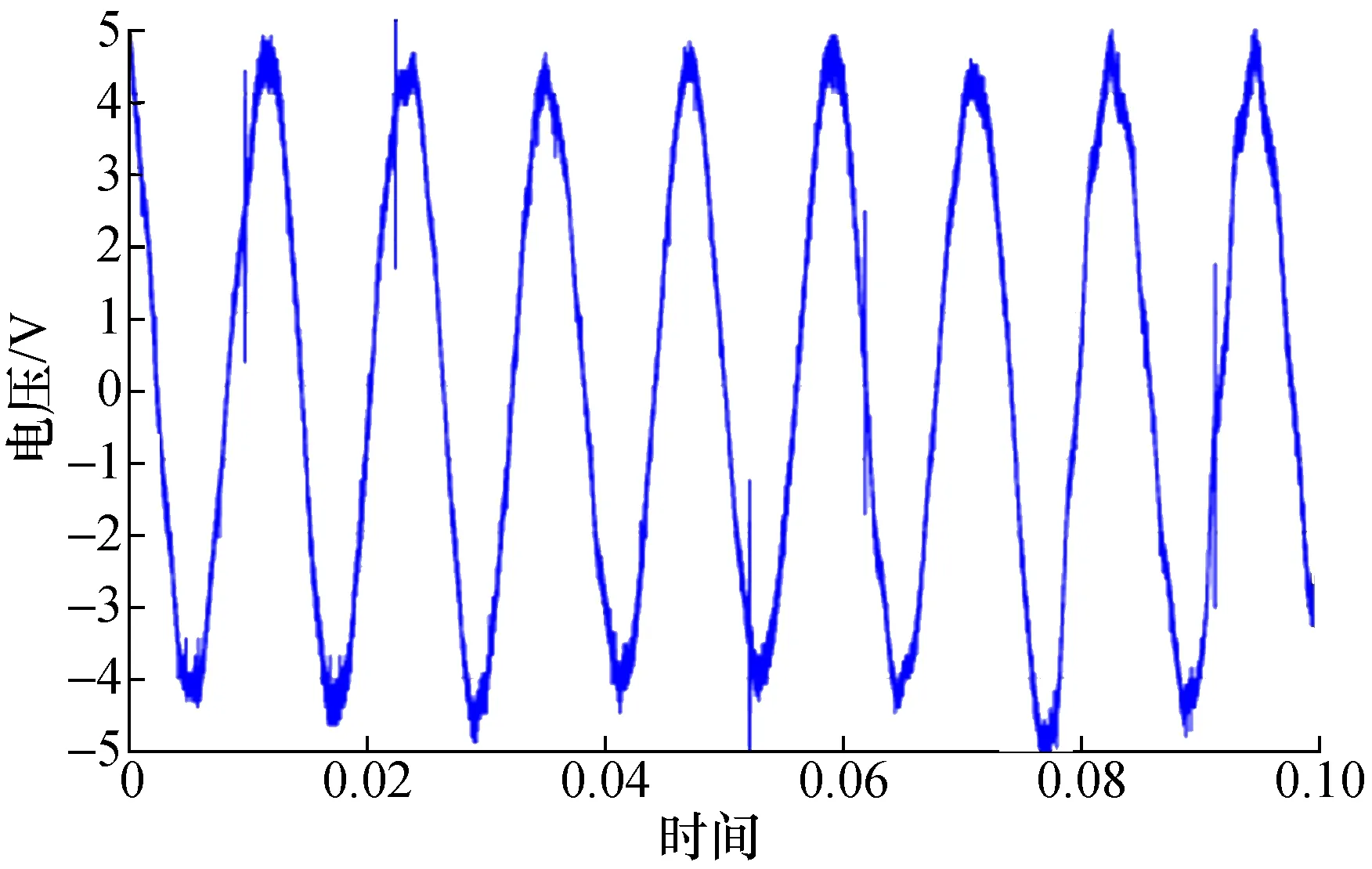
图18 转子对齐时370 r/min转矩脉动波形图Fig.18 Torque ripple waveform of 370 r/min

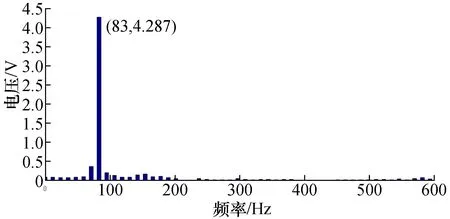
图19 370 r/min转矩脉动波形频谱分析图Fig.19 Spectrum analysis of 370 r/min torque ripple waveform

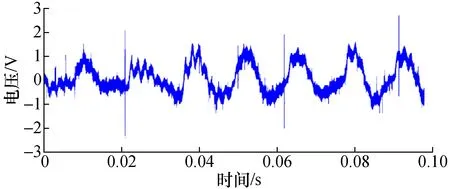
图20 370 r/min抑制后转矩脉动波形图Fig.20 Torque ripple suppression waveform on 370 r/min

图21 370 r/min抑制后转矩脉动波形频谱分析图Fig.21 Spectrum analysis of torque ripple suppression waveform on 370 r/min

由图7和图14、图9和图15可知,当定子磁极与转子凸极都相互对齐时(等效为合成一台电机的结构形式),转矩脉动相位相同,此时转矩脉动叠加,幅值约为单台SRM的2倍;由图14和图18、图15和图19可知,当转子凸极位置错开15°机械角时,转矩脉动相位约错开180°,此时转矩脉动叠加后幅值明显减小,与单台SRM测量到的转矩脉动波形幅值相比降低了60%左右。

5 结 论

目前大多数的SRM脉动转矩抑制主要是从控制策略的优化和定转子的结构上面的改进,一定程度上降低了转矩脉动,但抑制效果不甚理想。本文以三相6/4极的SRM为研究对象,在线性模式下理论分析了转矩脉动产生的原因,通过仿真验证了以换相为主频的脉动转矩是真实存在的,并且进一步通过永磁旋转角加速度传感器测得以换相为主频的脉动转矩近似呈现为周期变化的正弦曲线。从转矩脉动的周期性规律和峰谷波形近乎对称出发,提出了基于峰谷互补方法的SRM转矩脉动抑制。此方法与传统的控制方法相比,是从源头上消除SRM切向的脉动转矩,能更好地抑制脉动转矩。通过实验验证了该方法的可行性,且以换相为主频的脉动转矩抑制效果与单台脉动转矩相比降低了50%到60%之间。然而平台安装时候的同心度必然存在一定的误差,接下来进一步的研究方向是把2套磁路共用同一根主轴,理论上能够进一步抑制SRM切向的脉动转矩。