柔性支撑控制力矩陀螺动力学建模与控制

鲁 明,梁柱林,徐张凡

1.北京控制工程研究所，北京 100190 2.南京航空航天大学机械机构力学及控制国家重点实验室，南京 210016

0 引 言

控制力矩陀螺(control moment gyroscope，CMG)是航天器姿态控制的核心惯性执行机构.CMG通过高速转子高速恒速旋转获得角动量，通过框架电机调整转子系统的角动量矢量方向输出控制力矩，从而实现对航天器的姿态控制.可见，框架电机的伺服控制性能直接影响到控制力矩陀螺的力矩输出性能.

CMG是星上主要的微振动源之一[1]，为避免微振动对星体敏感载荷的影响，CMG需要安装在柔性隔振平台上，抑制CMG的微振动干扰传递，保持星体的低扰振水平.而隔振平台在抑制CMG微振动传递的同时，其自身在外部力矩激励的作用下会发生形变，从而改变CMG系统角动量矢量方向，影响CMG输出力矩的控制精度，进而影响航天器平台的姿态控制精度和稳定度.

文献[2-4]较全面地分析了CMG的动力学不确定因素，文献[5-9]从机械模型和电磁模型两方面入手，建立了CMG的动力学模型，可以用来分析CMG的动力学行为并指导控制系统设计.但文献[2-9]针对CMG框架控制系统的研究均为在刚性支撑基础上的控制研究，并未考虑柔性支撑条件.文献[10]研究了CMG集群隔振平台的动力学及其对卫星姿态控制的影响，给出在隔振条件下卫星姿态控制系统的参数选择方案.文献[11]则研究了CMG加入单机隔振平台后的动力学模型及其对卫星姿态的影响.但文献[10-11]的研究主要集中在CMG引入柔性支撑后对整星姿态控制的性能影响分析.文献[12]分析了柔性支撑所引发的CMG角动量矢量的改变及其对CMG输出力矩的影响，但其主要分析了柔性支撑条件下CMG整机的开环特性，未涉及柔性支撑对框架伺服系统闭环控制性能的影响分析和控制器设计.针对CMG自身动力学影响，尤其是柔性支撑对CMG自身控制性能影响的动力学分析及其控制策略，目前相关研究成果较少，亟需针对这一问题进行深入研究.

图1 安装在柔性隔振器的SGCMGFig.1 SGCMG installed on flexible vibration isolator

为抑制柔性隔振机构引起的扰动对CMG框架控制性能的影响，本文以单框架控制力矩陀螺(single gimbal control moment gyroscope，SGCMG)为基础，定义了4类坐标系，推导柔性支撑下SGCMG动力学模型及新增扰动力矩的模型，并设计了一种积分滑模控制器，实现框架系统的高精度闭环稳定控制.

1 坐标系建立

SGCMG安装在具有4个柔性隔振器的底座平台上，其动力学系统中涉及多部件的协同运动，需要建立以下坐标系对其运动进行描述：

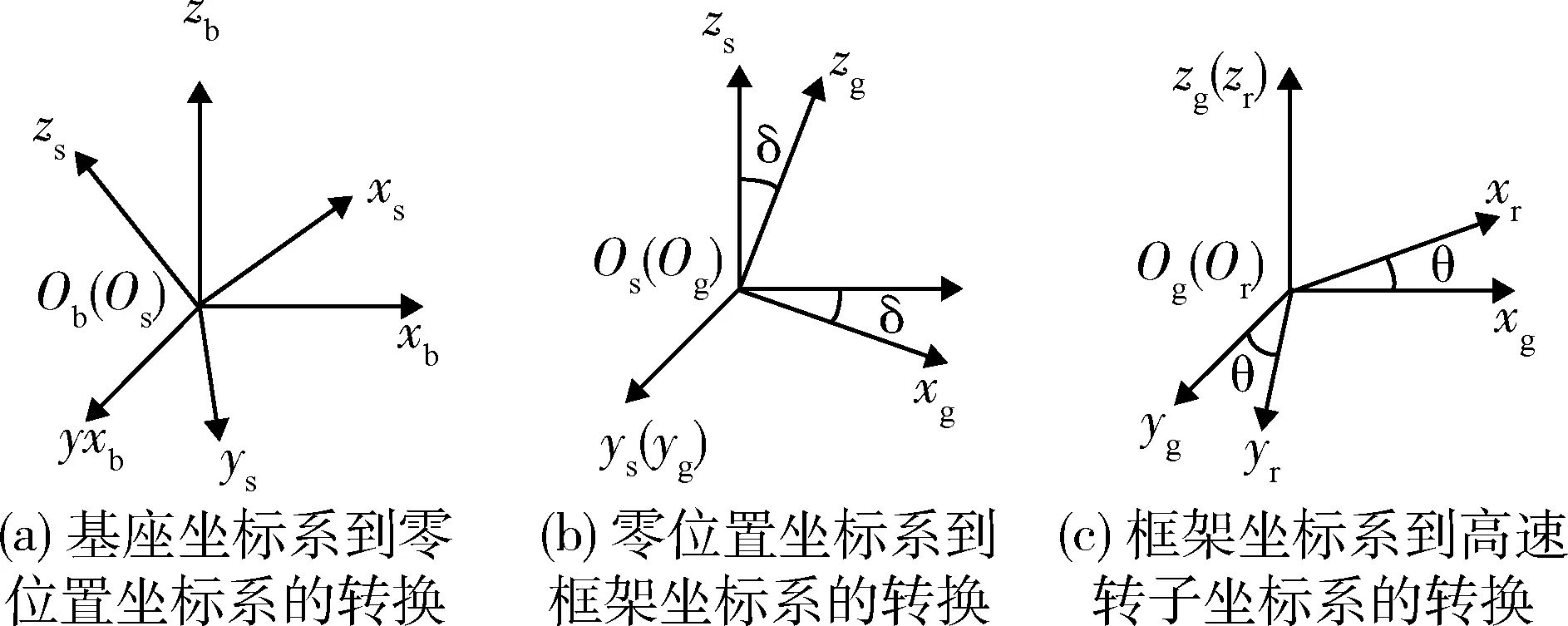
图2 坐标系的转换Fig.2 Coordinate transmission

1)基座坐标系Obxbybzb：基座坐标系xb轴和yb轴垂直且皆位于4个隔振器的支撑面，其中yb轴正向为SGCMG框架轴正向方向，zb轴垂直于xbyb轴平面并满足右手法则.

2)零位置坐标系Osxsyszs：零系与本体系固连，原点位于SGCMG质心.忽略零系和基座坐标系的位置矢量，考虑柔性支撑的柔性，零位坐标系由基座坐标系沿X-Y-Z顺序旋转(α-β-γ)角度得到.

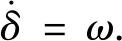
2 柔性支撑SGCMG动力学建模

假设基座与地面固连，考虑柔性支撑的柔性形变，基于拉格朗日方程建立柔性支撑条件下的SGCMG框架动力学模型.

在惯性系Obxbybzb上SGCMG系统的动能为

W=Wr+Wg+Ws=

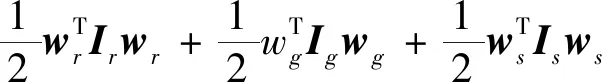
(1)

式中，Ir=diag{Irx,Iry,Irz}、Ig=diag{Igx,Igy,Igz}和Is=diag{Isx,Isy,Isz}分别为高速转子、框架和柔性支撑的惯性张量，Ir、Ig、Is的取值可由有限元计算或实验测量得到.wr，wg，ws分别是惯性坐标系下高速转子、框架和柔性支撑的转速，Wr、Wg、Ws分别为高速转子、框架和柔性支撑的动能.

系统势能为隔振机构柔性形变引起的弹性势能，其表达式为

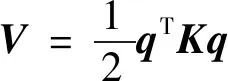
(2)

式中，q=[αβγ]T是由柔性支撑三轴形变组成的广义矩阵变量，K=diag{kx,ky,kz}为柔性支撑的弹性刚度矩阵.

系统阻尼采用线性粘性阻尼模型，阻尼力与广义速度成正比，此时瑞利耗散函数为

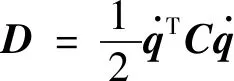
(3)

式中，C=diag{cx,cy,cz}为柔性支撑的阻尼矩阵.

基于能量法，采用拉格朗日方程建立动力学方程.综合式(1)至式(3)，计算得拉格朗日函数为L=W-V,代入拉格朗日方程中得

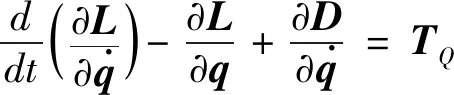
(4)

式中，TQ=[TQxTQyTQz]T为作用在柔性支撑上的广义力矩，

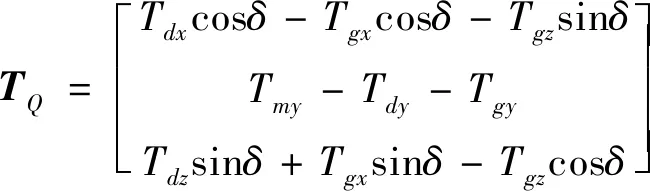
(5)

其中，Tm为柔性支撑SGCMG框架电机启动力矩，

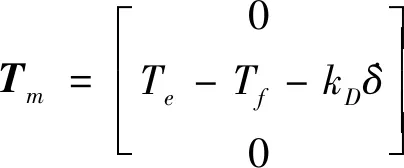
(6)

式中，Te为框架电机电磁力矩，Tf为框架摩擦力矩，摩擦力矩采用LuGre模型表征[15].kD为框架阻尼系数.

Td为动不平衡力矩

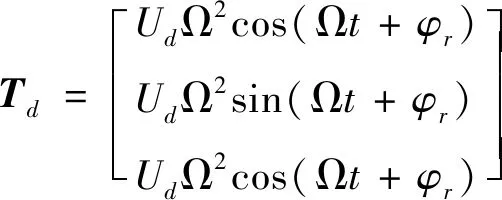
(7)

式中，Ud为高速转子动不平衡量，φr为高速转子初始相位.

Tg为陀螺力矩，可由动量矩守恒定理计算得出.在高速转子坐标系Orxryrzr上，高速转子的转动惯量为I=diag{Ix,Iy,Iz}，由于高速转子的对称结构，转子的赤道转动惯量Ix=Iy，Iz为极转动惯量.令高速转子的动量矩为H，则有

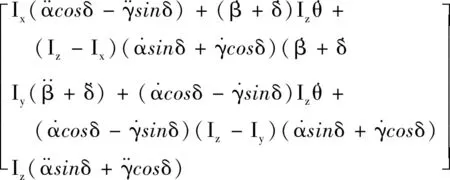
(8)

综合式(1)-(8)，计算可得

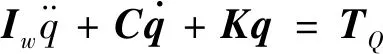
(9)

其中

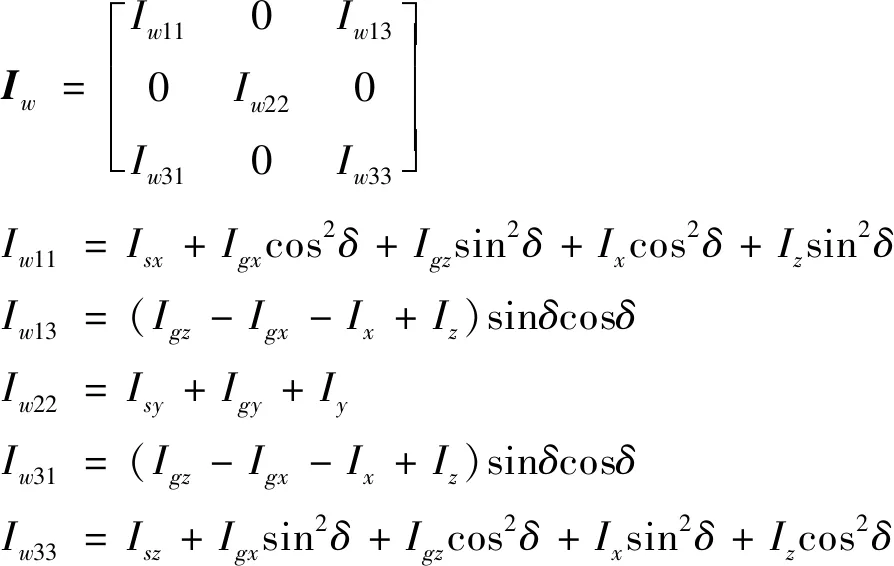
(10)

根据式(9)可解出柔性支撑三轴角位移α、β、γ，进而获得柔性支撑在框架轴引起的扰动力矩Tgy的解析模型如下：

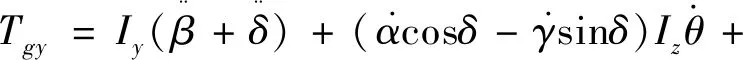
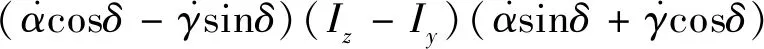
(11)

3 柔性支撑影响分析

柔性支撑的三轴形变改变了SGCMG角动量矢量的方向，在低速框架轴方向产生干扰力矩分量Tgy，同时其自身柔性运动与框架系统产生动力学耦合，导致框架系统参数摄动，改变框架轴的动力学特性.

柔性支撑SGCMG框架系统PID控制仿真系统如图3所示.其中，SGCMG框架采用永磁同步电机(PMSM)直接驱动，干扰力矩包括摩擦干扰、高速转子动不平衡干扰和柔性支撑引起的干扰力矩，控制对象模型中考虑柔性支撑引入的耦合动力学，控制策略采用PID控制.分析PID控制策略下柔性支撑对控制系能的影响.系统模型参数如表1所示.

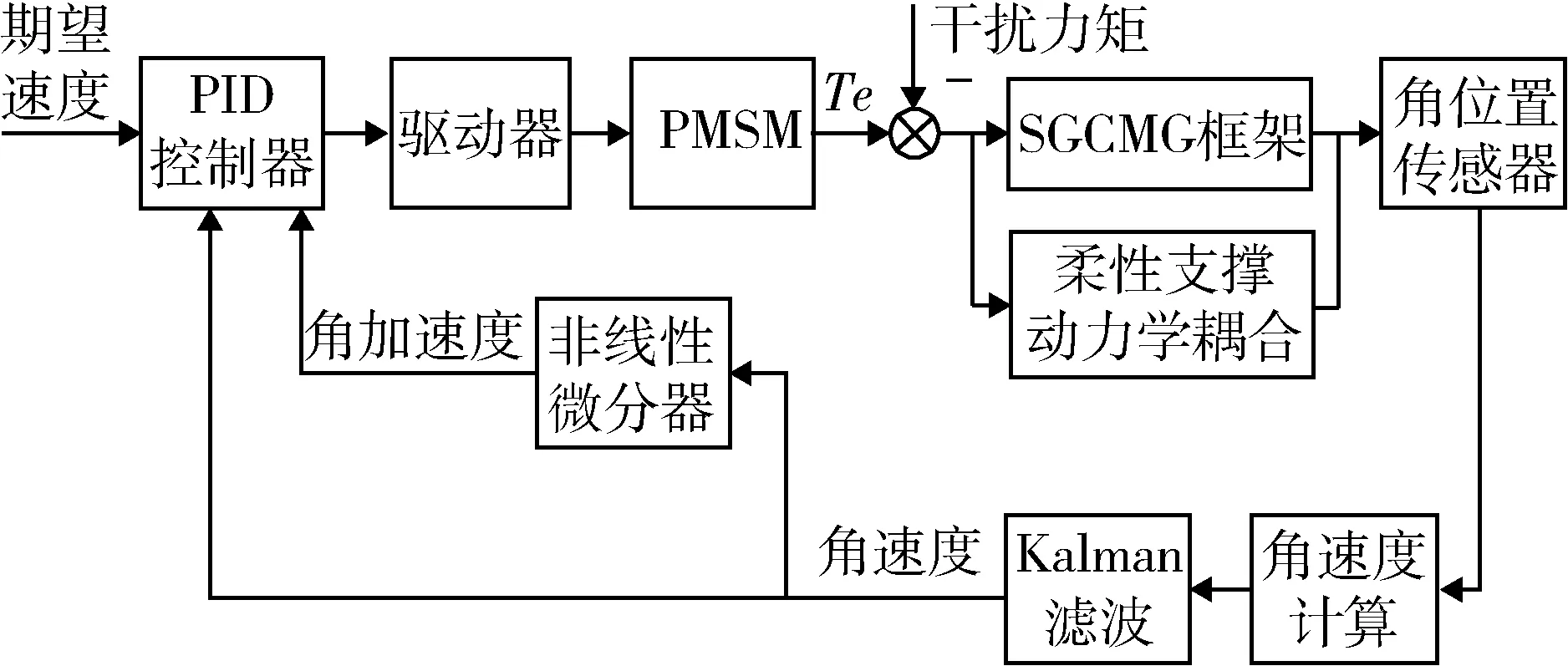
图3 柔性支撑SGCMG框架系统PID控制框图Fig.3 PID controller for SGCMG gimbal system with flexible support

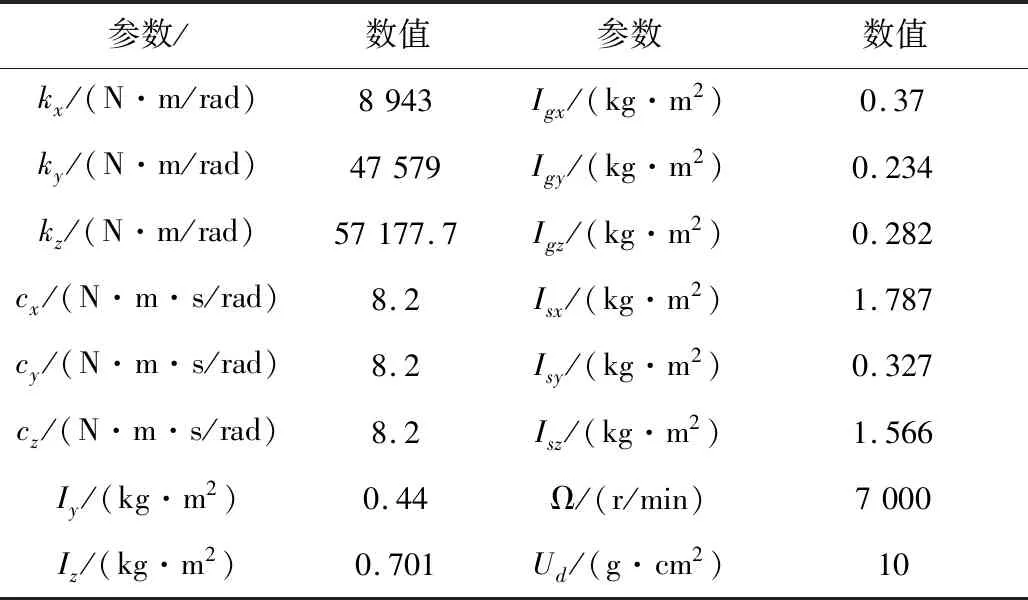
表1 系统模型参数表Table 1 System model parameters

在PID控制策略下，柔性支撑在三轴方向上的形变如图4.当在框架速度为1°/s时，X、Z轴形变最大幅值分别为0.001°和0.000 16°，Y轴的形变量最小.三轴形变的幅值不同是由于柔性支撑三轴的刚度不同引起.柔性支撑的三轴形变量随着框架位置的变化而变化，周期与框架位置变化周期一致.

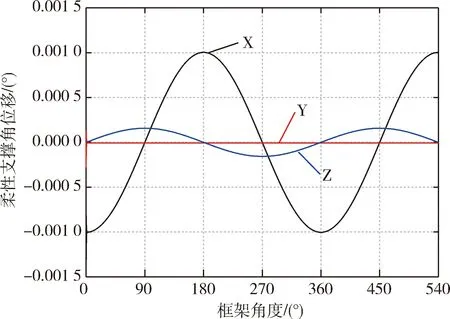
图4 柔性支撑三轴形变角位移Fig.4 Threeaxis angular displacement of flexible support

引入柔性支撑后SGCMG框架轴新增干扰力矩曲线如图5.框架转速为1°/s时，柔性支撑引起的扰动力矩最大幅值为0.037 9 N·m，周期为180.0 s；框架转速为2°/s时，扰动力矩最大幅值为0.152 N·m，周期为90.0s.可见，在柔性支撑下，框架转动速度越大，扰动幅值越大.当SGCMG支撑为绝对刚性时，该扰动分量为零.

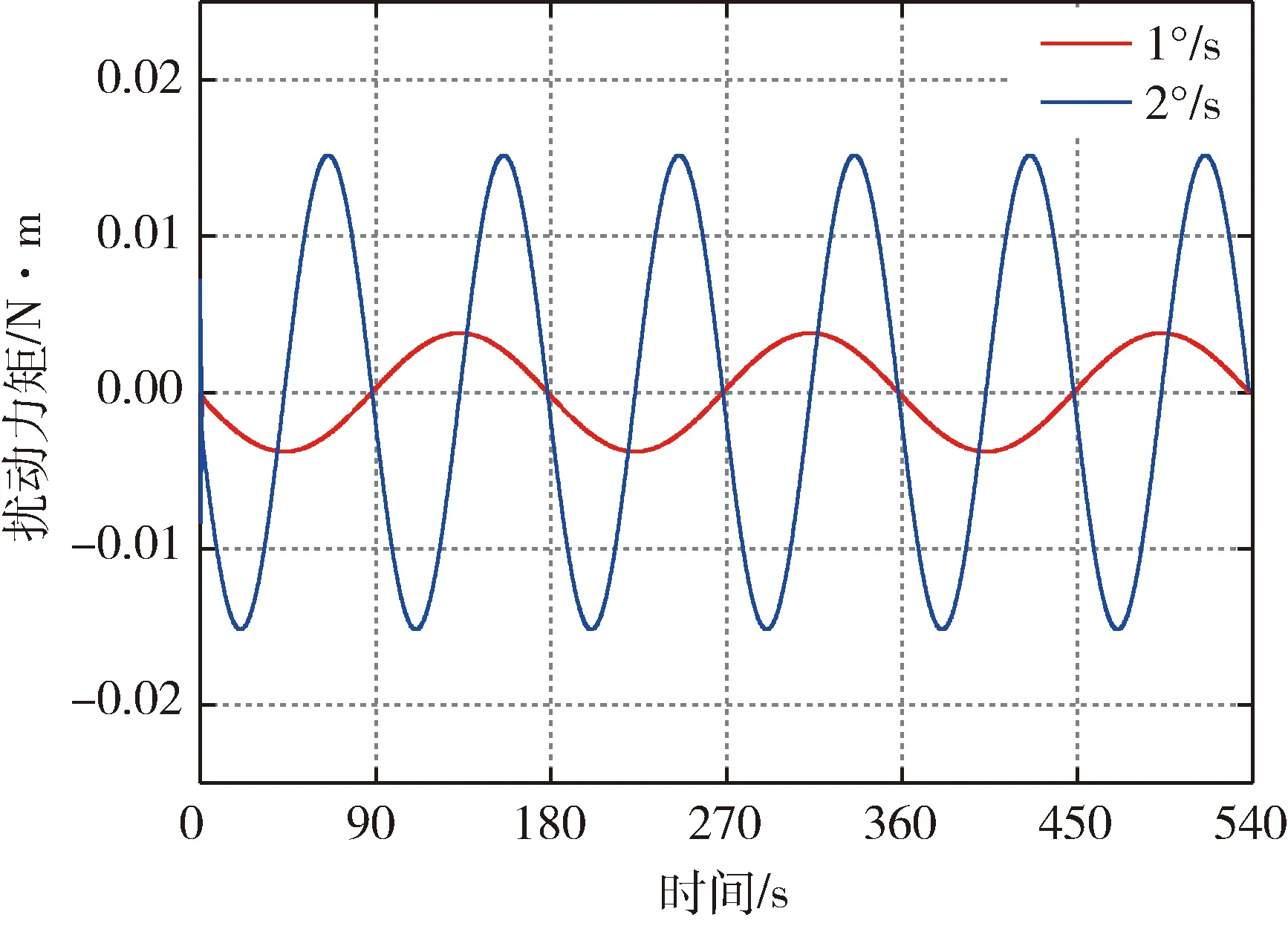
图5 不同框架转速时柔性支撑在框架轴的引起扰动力矩Fig.5 Disturbance torque of flexible support on gimbal axis under different gimbal speed

引入柔性支撑前后框架速度阶跃响应对比曲线如图6.引入柔性支撑前，框架速度阶跃响应无超调，稳定时间为0.41 s；引入柔性支撑后，若PID参数不变，阶跃响应性能变差，优化参数后，超调量变为5.96%；稳定时间为1.31 s，是引入柔性支撑前的稳定时间的3倍.

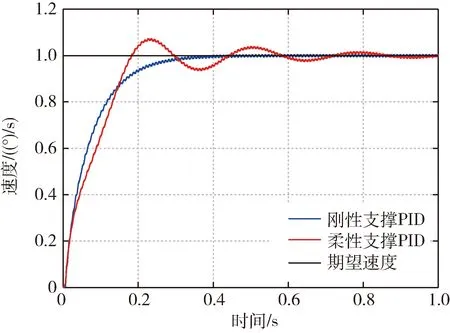
图6 引入柔性支撑前后PID控制框架速度阶跃响应Fig.6 Gimbal speed step response of PID control before and after introducing flexible support

可见，SGCMG框架系统引入柔性支撑后，框架系统的动力学特性发生变化，同时新增了干扰力矩，传统的PID控制难以同时兼顾框架转速的动态性能和稳态性能，导致框架速度控制性能下降.

4 滑模控制器设计与仿真分析

具有滑动模态的滑模控制策略对系统的参数摄动和力矩干扰具有较强的鲁棒性，可以通过滑动模态的设计使系统轨迹快速进入滑模面，提升系统的动态性能，进入滑模面后通过变结构切换控制保证系统的稳态性能.因此，滑模控制策略在兼顾保证动态性能鲁棒性和稳态性能鲁棒性方面具有优势[14].

在柔性支撑SGCMG系统动力学模型的基础上，设计一种积分滑模控制器(sliding mode control，SMC)实现系统闭环稳定控制.

综合前文推导，可知伺服系统模型为

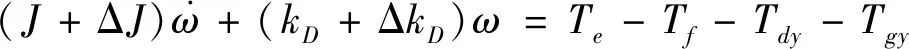
(12)

式中，J=Iy+Igy为框架电机转动惯量，ΔJ、ΔkD为柔性支撑在框架轴引起的参数摄动.

取式(12)的标称模型，可得

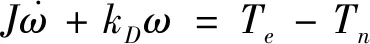
(13)

其中，Tn=Tf+Tdy+Tgy为框架轴集总干扰力矩.框架电机电磁力矩Te=kTi，kT为电机转矩系数，i为电机力矩电流，其表达式由下式微分方程计算

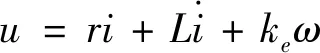
(14)

式中，r、L分别为电机电阻和电感，ke为电机反电势系数.

综合式(13)和(14)，可求

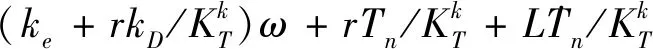
(15)

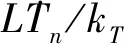
(ke+rkD/kT)ω+rTn/kT

(16)

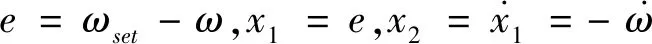
kT(ke+rkD/kT)ω/LJ+rTn/LJ

(17)

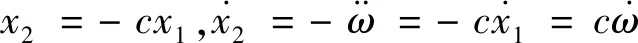
(18)

进而可求

kT(ke+rkD/kT)ω/LJ+rTn/LJ

(19)

则可求得等效控制ueq为

(ke+rkD/kT)ω+rTn/kT

(20)

滑模控制器采用指数趋近律，则可求电机控制电压为

u=ueq+ks+δsat(s)=

(ke+rkD/kT)ω+rTn/kT+ks+δsat(s)

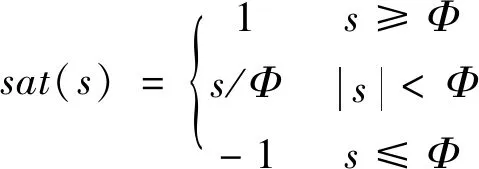
(21)

式中，k>0,δ>0,Φ>0.sat(s)函数用于降低系统轨迹进入滑动模态后趋近律中的符号函数切换引起的高频抖振.

滑模系统控制框图如图7所示，将PID控制器替换为滑模控制器，其他仿真条件与第3节一致.在动力学特性变化和新增干扰力矩的影响下，对比滑模控制策略在引入柔性支撑前后的控制性能；并在柔性支撑条件下，与PID控制策略的控制性能进行对比.

如图8所示，在柔性支撑干扰力矩、摩擦干扰力矩、动不平衡干扰力矩的影响下，PID控制的阶跃响应上升时间为0.14 s，SMC的上升时间为0.07 s，相比PID提升了50.0%，可见，SMC具有较优的动态性能.进入稳态阶段后，PID控制器对扰动力矩具有一定的抑制效果，框架转速在0.995°/s到1.005°/s间波动，波动量为0.5%；SMC控制策略的稳态波动在0.999 9°/s到1.001 1°/s间波动，最大波动量为0.1%，稳态性能比PID控制提高了5倍.

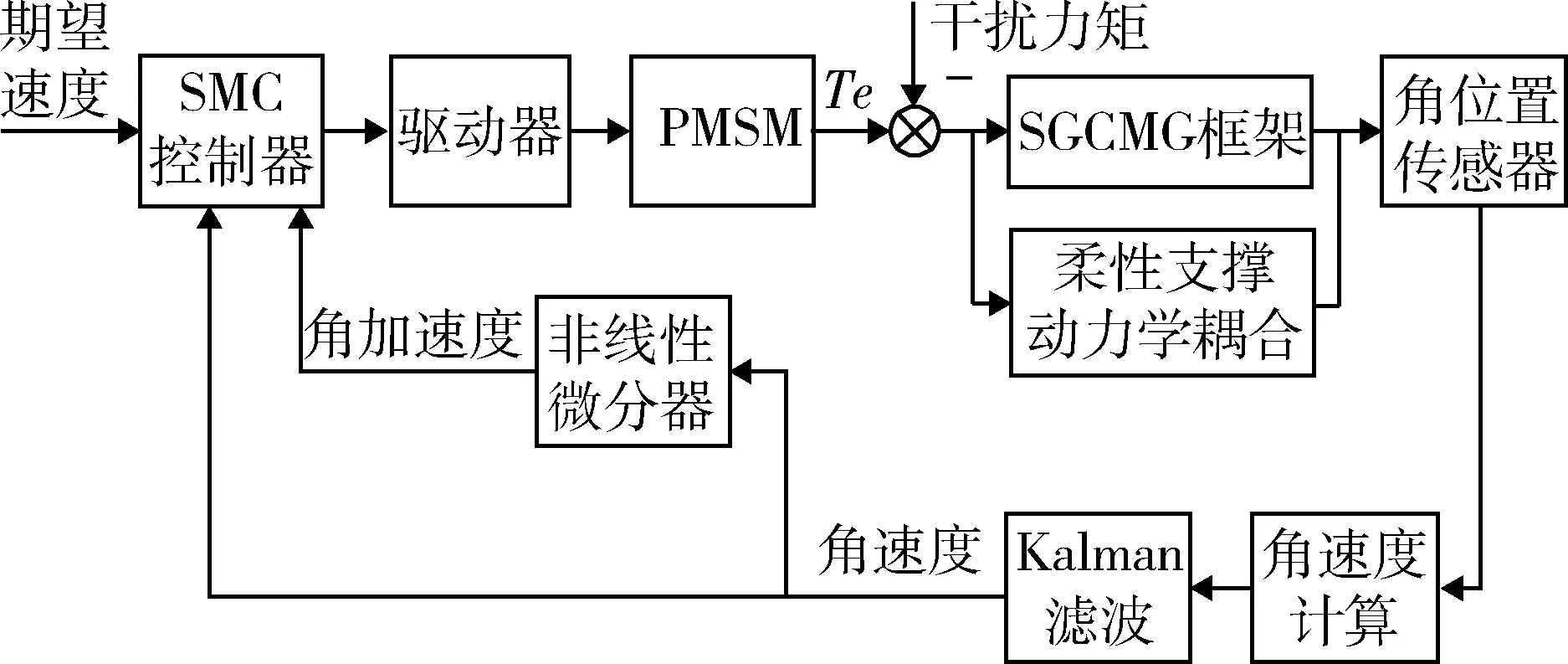
图7柔性支撑SGCMG框架伺服系统控制框图Fig.7 SMC controller for SGCMG gimbal system with flexible support

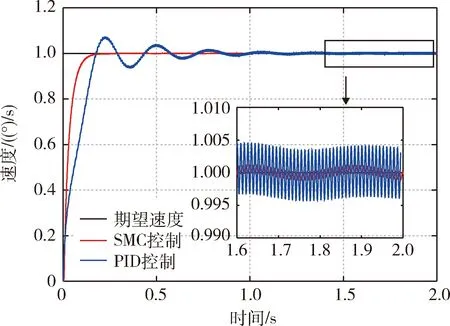
图8 柔性支撑SGCMG框架速度控制阶跃响应Fig.8 Step response of SGCMG gimbal system with flexible support

综上，相对传统的PID控制，本文设计的SMC控制策略具有良好的动态响应性能和稳态性能，能够有效抑制柔性支撑扰动等干扰力矩的影响，提高SGCMG框架系统的控制精度.

5 结 论

本文首先通过拉格朗日方程建立柔性支撑条件下SGCMG的动力学模型，并给出柔性支撑引入干扰力矩的解析模型.然后，在PID控制策略下分析了动力学变化和新增干扰力矩对控制性能的影响.据此，设计了一种积分滑模控制器，相比传统的PID控制具有更好的动态过程和稳态性能，提升了柔性支撑下控制力矩陀螺框架速度的闭环控制性能.