一种基于OPTICS聚类的仅测角导航目标检测算法
王 宁,汪 玲*,徐 根,杜荣华,张 翔
1.南京航空航天大学,南京 211106 2.南京理工大学,南京 210094
0 引 言
随着空间活动商业化的快速发展,对低成本高可靠性的导航技术有了更广泛的需求.由于卫星对地通信条件的限制,在导航过程中应尽可能减少地面工作站的远程控制,要求在导航过程中具有较高的自主性.在众多的自主导航技术中,仅测角自主导航方法具有设备简单、复杂度低,功耗低的优点,适用于成本较低的微纳卫星,满足商业化的要求.
在中远距离下,由于无法获得目标的姿态信息,需要配合距离及目标视线角[1]或仅使用目标视线角[2]完成导航.而在自主导航抵近过程中当前主要使用光电传感器来获取目标视线角信息.由于空间中光照环境复杂,目标信息少,稳健的空间目标检测算法成为了仅测角导航的关键[3].
针对仅测角导航中的空间目标检测算法,国外已经在展开了深入研究并率先完成了相关在轨实验[4-5].2012年德国航空航天中心主持了ARGON (advanced rendezvous demonstration using GPS and optical navigation)在轨实验使用由丹麦技术大学研制的视觉模块,实现了30~3 km范围内的抵近.ARGON实验在目标检测算法上,首先利用飞行器姿态信息及星表对提取出的点进行识别,将其分为恒星点及非星目标点.对两帧中的恒星点及非星目标利用灰度信息定义了任意两个点之间的相似因子,并使用Kuhn-Munkres匹配算法将两帧中的非星目标或恒星的对应的点匹配在一起.最后分别计算出匹配在一起的点在两帧图像之间的位移.由于相机热点在像素块中的位置基本不变,位移小于特定门限的点可作为相机热点排除.针对其他点,计算出点在成像平面内的平均位移.由于恒星与目标之间的运动差异,与平均位移相差大于一定门限的点被判断为目标.2016年,德国航空航天中心在ARGON实验的基础上,完成了AVANTI (autono-mous vision approach navigation and target identification)在轨实验[6].相比ARGON实验,AVANTI实验仅使用运动信息来实现目标轨迹的提取,在自主抵近目标的过程中不再使用GPS定位信息且降低了对空间光照条件的限制.
国内学者对空间目标检测进行了大量理论分析.有学者提出用最小二乘估计方法估计目标的运动轨迹[7],该方法算法简单、运算量小,但对于在视野中非直线运动的目标,估计误差会随着目标运动不断变大.还有学者提出了先用交叉投影生成恒星掩膜后确定目标的方法[8]、基于全局运动参数估计的方法[9]、基于卡尔曼滤波器的算法[10]、迭代距离分类与轨迹关联检测的方法[11]等其他一些方法.考虑到这些方法或需要限制目标运动轨迹为直线、或需要识别图像中所有恒星、或需要进行序列图像的配准,而AVANTI实验中的算法避免了这些限制,且在轨实验显示了其高效性.本文在其基础上进一步深入研究并进行了改进.
AVANTI实验中目标检测算法不足之处在于其使用的DBSCAN(density-based spatial clustering of applications with noise)聚类算法具有对参数邻域半径和密度阈值敏感的特性,最终在检测目标以及抵近目标的过程中需要人工依据经验调节聚类参数,在自主性上仍然存在提升空间.本文使用的OPTICS聚类对参数相对不敏感,并对聚类距离进行修正,从而更好的提取出目标轨迹.
本文第1节介绍了空间目标的成像模型及目标检测算法处理流程,其中详细分析了针对聚类算法的改进,目标轨迹的形成.第2节使用仿真星图分别验证了在仅测角导航过程中对目标的初次检测以及抵近过程中本文中算法的可行性.最后一节,对算法进行了简要总结.
1 目标检测算法
光电传感器采集得到的图片中,由恒星、目标、背景噪声及可能出现的相机噪声组成.对于空间中任意赤经为α赤纬为δ的恒星,在J2000坐标系下的方向矢量表示为
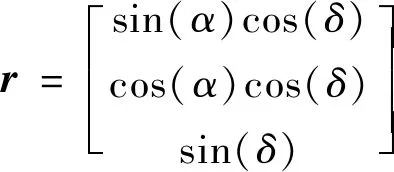
(1)
设相机相对于J2000坐标系的旋转矩阵表示为R,则恒星在成像平面内的位置表示为(xs,ys),则(xs,ys)与r满足方程[2]
(xs,ys)=h(R·r)
(2)
其中h(v)表示对v进行投影变换.由于单个像素的定位精度无法满足姿态测量的要求,因此通常使用离焦处理使得星点在像素平面上扩散到多个像素块[12],即(xs,ys)通常在像素平面通常会占据多个像素块.因此,需要首先对采集得到的图片进行星图预处理提取出满足精度要求的星点及目标点.
为了形成恒星及目标运动轨迹,需要使用多帧图片.由于恒星在成像平面中的位置在相邻两帧中的位移变化通常十分微小,若直接选择短时间内的连续帧图片用于目标检测,则难以区分恒星与相机热点,且在使用聚类算法时会引入较大的计算量.由此,本文结合星图识别的结果从中选择出部分帧用于目标检测,将其称为关键帧.
青辰已经越来越接近地面,箭囊中的箭矢也即将告罄。他知道,如果在他落地之前,不能将地面的这些土狼驱散的话,他将会与那女子一样,陷入土狼的包围圈中。
对于选择出的关键帧,使用经过改进的OPTICS聚类算法即可获得轨迹,若其中仅包含一个目标轨迹,可直接由运动差异选择出目标.当包含2个及以上目标时,则需要分别对轨迹进行拟合,并依据拟合参数选择目标.目标检测算法的完整流程图如图1所示.
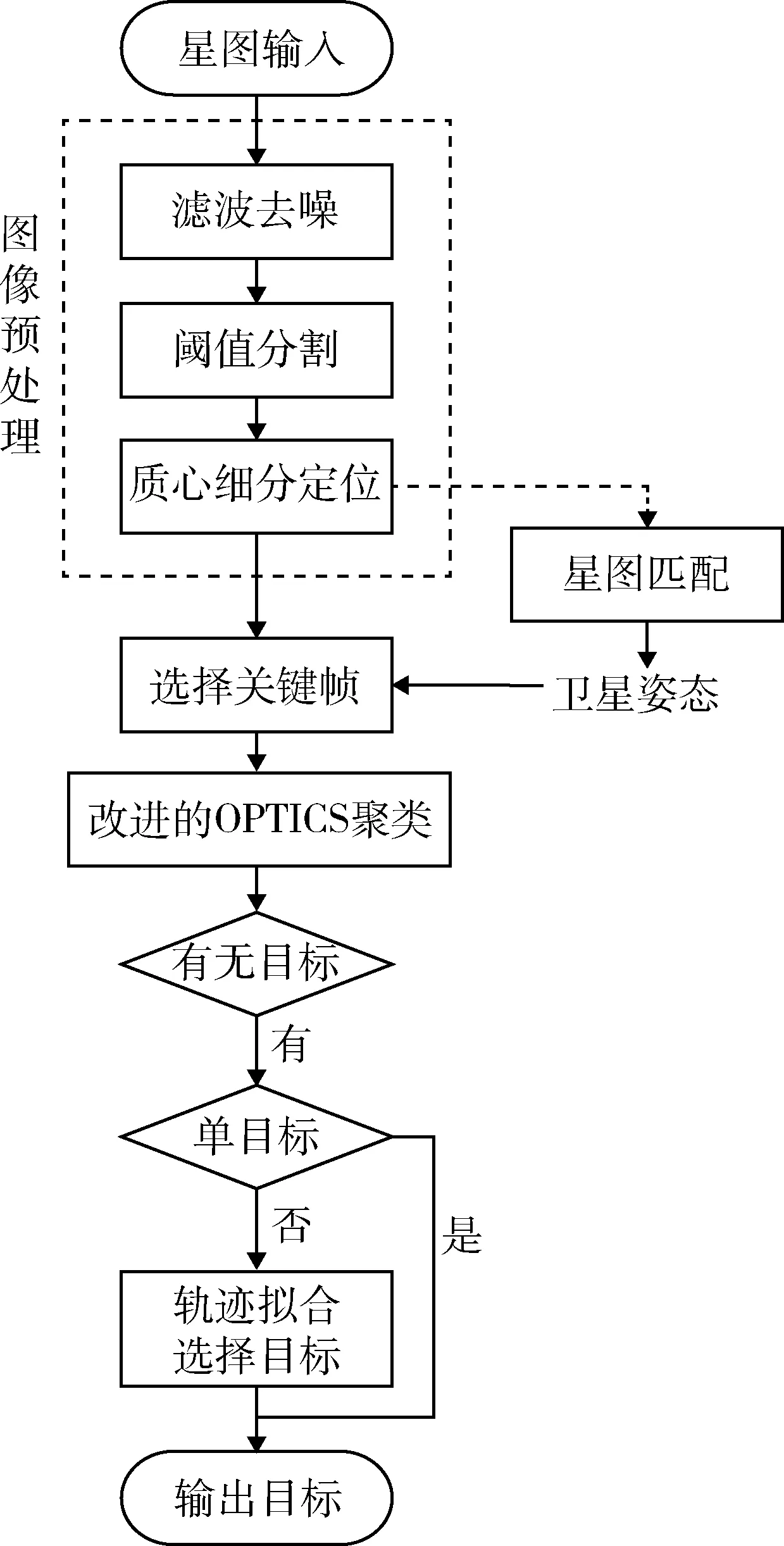
图1 目标检测流程图Fig.1 Flow chart of target detection
下面分别对该目标检测流程中的图像预处理、关键帧的选择和改进的OPTICS聚类方法进行详细介绍.
1.1 图像预处理
图像预处理主要包括:图像滤波、图像分割、连通域分割和星点的细分定位.图像采集电路得到的原始信号中夹杂着大量的噪声,通常首先使用3×3或5×5的低通滤波模板滤波.图像分割的目的在于使用全局阈值或局部阈值[13]将星点目标与背景分开.连通域分割用于将星点及目标相互区分开来[14-16].星点的细分定位用于提高星点定位精度,从而达到亚像素级,常用的方法包括质心法及其改进算法[17]、曲面拟合法[18]等方法.其中质心法及其改进算法具有复杂度低、稳定性好的优势,在工程中得到了广泛的应用.
1.2 关键帧选择
经过图像预处理后任意星点或目标点可以表示为(x,y,k),其中(x,y)表示星点或目标在成像平面的坐标,k表示帧序号,并把第一帧加入关键帧.将提取出的星点与导航星表匹配后,某一颗被识别出恒星在第k1帧与第k2帧中的坐标分别表示为(x1,y1,k1)及(x2,y2,k2),该恒星在两帧之间的欧式距离d(k1,k2)表示为

(3)
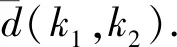
1.3 改进的OPTICS聚类
OPTICS聚类[19-20]是一种经典的基于密度的聚类方法,从任意一个数据对象开始,尽量向着密度大的方向扩张,按照扩张顺序将每个数据对象依次排列(即有序序列),画出可达距离,则形成了反映簇结构的决策图.以下将简要介绍核心距离、可达距离、密度直达的定义.对象P在参数ε和参数Minpt下的核心距离定义为:若对象P的ε邻域内的对象数大于等于Minpt,则其核心距离为第Minpt近的对象到对象P之间的距离.对象P到对象M之间的可达距离定义为:若对象P的ε邻域内的对象数大于等于Minpt,则对象P的核心距离与对象P和M之间距离的最大值即为对象P到对象M之间的可达距离.若对象P的ε邻域内的对象数大于等于Minpt且对象N在对象P的ε邻域内,则称对象N到对象P密度直达.
修正的原则是将同一帧中的不同点归为不同的类.假设关键帧中星点及目标点在同一坐标系下的轨迹如图2所示,其中绿色虚线对应目标的轨迹,黑色、蓝色和灰色虚线对应不同恒星性的轨迹.由于绿色轨迹在起始时刻的轨迹点接近黑色轨迹点,在末尾时刻的轨迹点接近蓝色轨迹,若直接使用欧式距离聚类,三条轨迹将聚类为一条,即无法正确区分目标和恒星.因此,应对距离修正,使一条轨迹末端与另一条轨迹首端之间的距离大于ε,即这个两个端点之间不是密度直达的,从而避免被归为同一类.
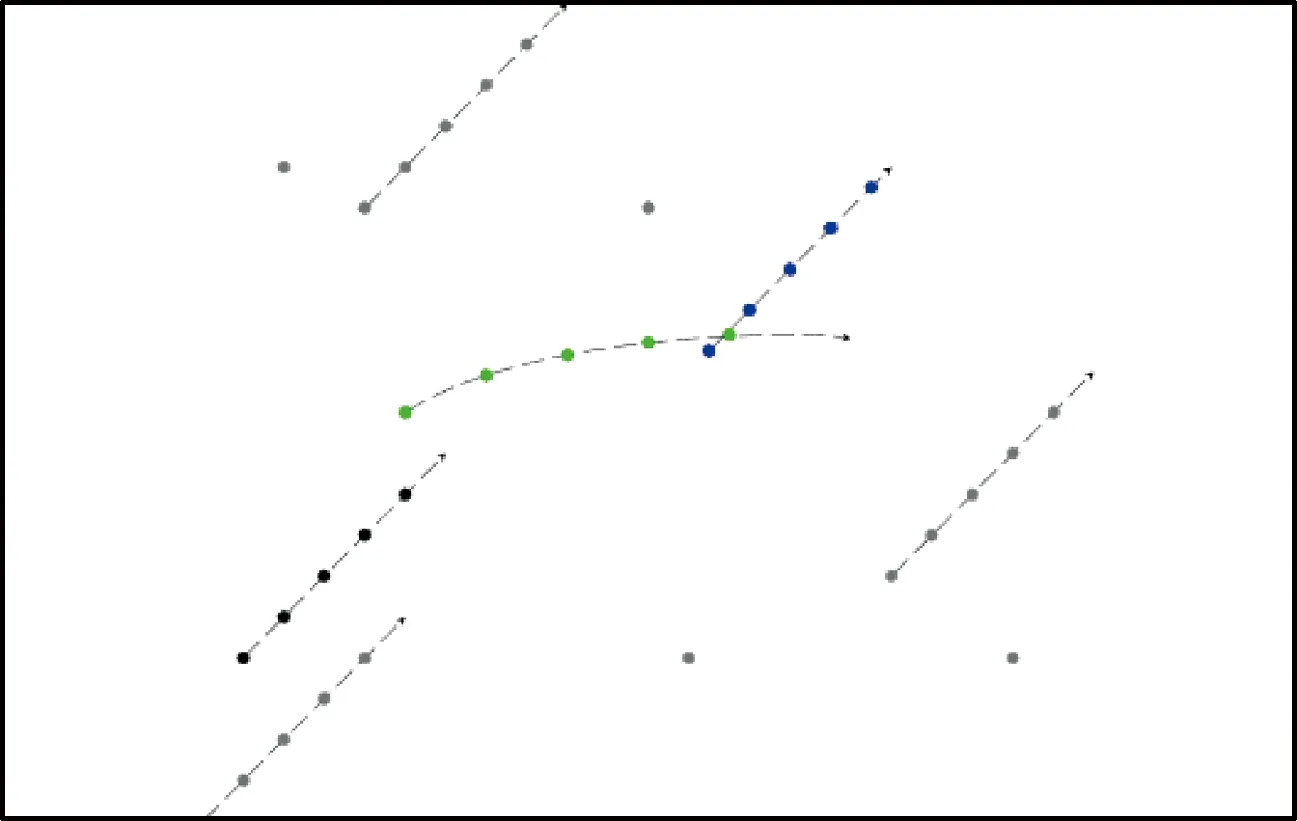
图2 关键帧中星点及目标Fig.2 Star points and a target in key frames
假设两个端点之间的关键帧序号之差大于Minpt,若修正后的距离大于Minpt·d(K1,K2)则其必然大于ε,这里将其修正为(Minpt+1)·d(K1,K2).对于有相同关键帧序号的两个点,显然不应将其归为同一类,则将其距离修正为无穷大,表示为inf.其它情况下,无需对距离进行修正.最终距离修正公式为:
d1(i,j)=
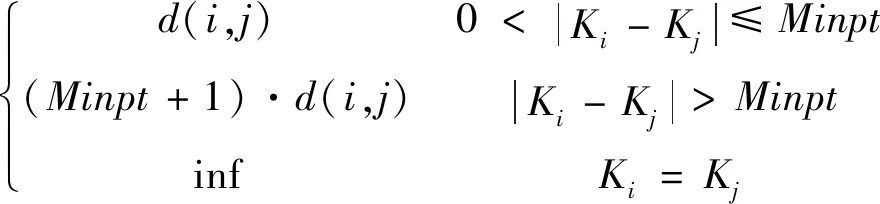
(4)
此外,对于同一轨迹中的两个点,若两点的关键帧序号之差大于Minpt,由两个点之间的轨迹点将其联系在一起,依然可以被聚为同一类,避免了此时距离修正引起的聚类错误.
使用OPTICS聚类算法,会首先生成一个有序排列,其中距离越接近的数据,在排列中的位置越靠近,更有可能被分为同一类.分别使用修正前后的距离聚类生成的决策图如图3(a)、图3(b)所示.图中横坐标为有序序列(又称扩张顺序),纵坐标为可达距离.当目标位置接近恒星时,则在决策图上表现为一个微小的尖峰将目标与该恒星区分开,即图中横坐标为32处对应的尖峰.修正后尖峰将得到放大,同时修正后的决策图中出现了新的尖峰,这是由仅在部分帧进入视野的目标引起的.
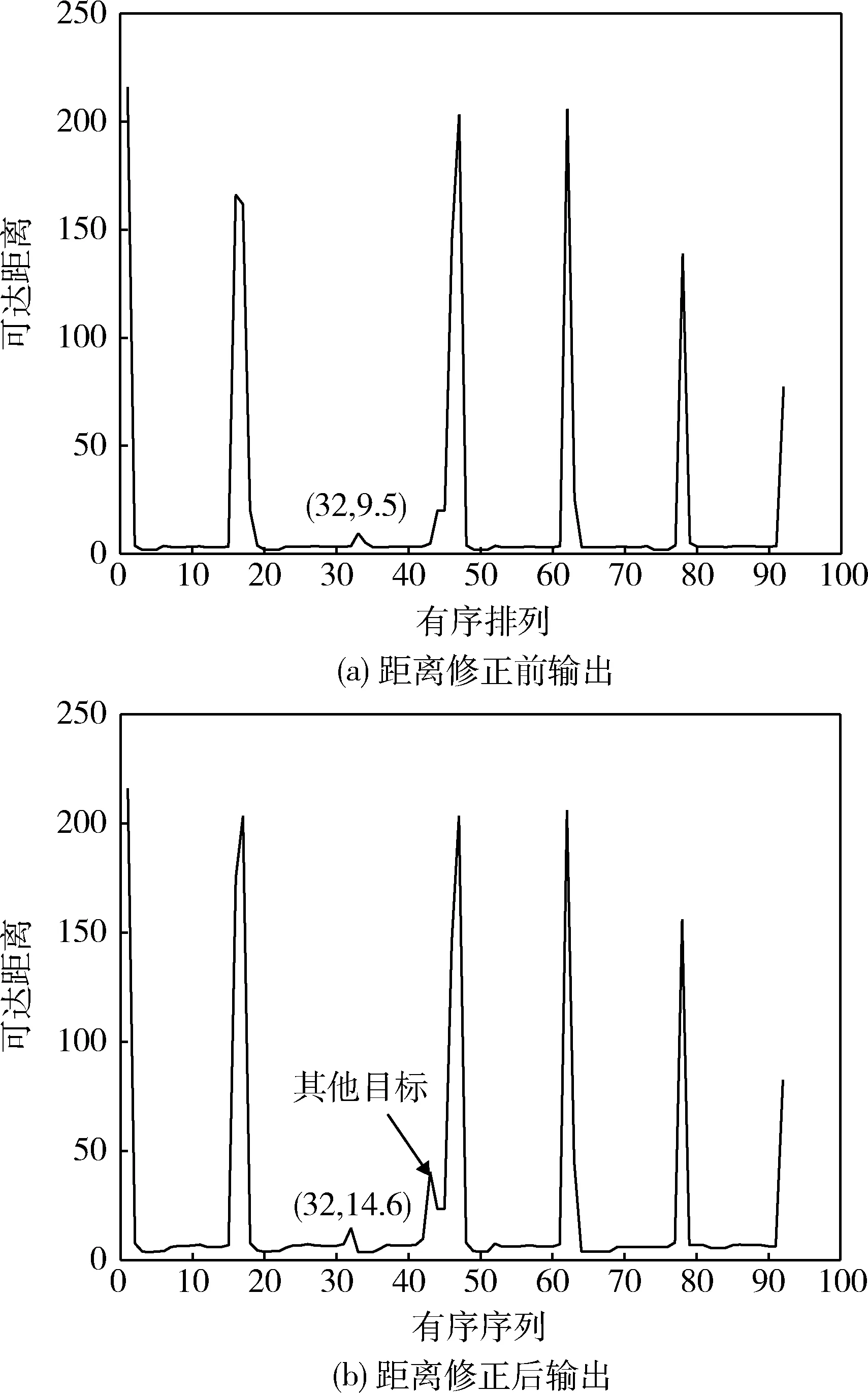
图3 OPTICS聚类输出有序序列Fig.3 Ordered arrangement output result of OPTICS
从决策图中自动识别簇完成分类任务,可用ε-Clustering[20]、Tree Clustering[21]等方法[22-23].其中Tree Clustering方法简单易用.本文参考Tree Clustering方法选择阈值.首先从决策图中选则局部最大值.对任意数据对象,若其相邻左侧数据对象的可达距离(如果存在)与其相邻右侧数据对象的可达距离(如果存在)的均值小于该数据对象可达距离的0.75倍,则该数据对象为局部最大值.遍历决策图选择出所有的局部最大值,并按照可达距离降序排序.然后依次在决策图中比较该局部最大值将其左右两侧分为两类是否合理.若新分成的两类中其中一类的数据数目小于预定义的最小类数目则认为不合理,否则认为其合理.最后,选择局部最大值序列中可以合理分类的最小可达距离的μ(0.75<μ<1)倍作为阈值.
2 仿真验证
在中远距离下,用于仅测角导航的目标检测算法,其工作阶段可大致分为两部分:卫星初次对空间目标的检测和伴飞抵近过程中对目标的检测.以下将分别仿真不同阶段的目标检测结果.关键帧选择参数n·σ为2.4像素,聚类参数Minpt=3,参数ε初始化为无穷大,阈值参数μ=0.8.
首先仿真了背景星图[24-26],仿真使用的探测器视场角为16.8°×12.6°,CCD分辨率为640×480,仿真了视星等6等及以上的SAO星表中的恒星.对星表中经过岁差、章动、自行修正后的恒星赤经、赤纬转换为J2000坐标系下的方向矢量,经过旋转投影变换从而得到恒星在成像平面中的坐标(xs,ys),其后对成像平面内的恒星在3×3像素范围内离焦并对并对灰度使用高斯函数拟合[26].
空间目标的等效视星等与卫星模型材质以及探测器CCD性质以及目标与卫星之间的距离有关,由于基于 OPTICS的目标检测算法中,未使用到星图中目标的灰度信息,在仿真过程中指定其等效星等为5.2.并对加入目标后的星图添加高斯噪声作为背景噪声,最终仿真出单帧星图如图4所示,对图中一颗恒星周围区域放大后如红色框中所示.

图4 仿真星图Fig.4 Simulation of star map
使用表1中的轨道初始参数进行轨道递推,仿真出连续的星图,帧之间时间间隔为0.1 s.
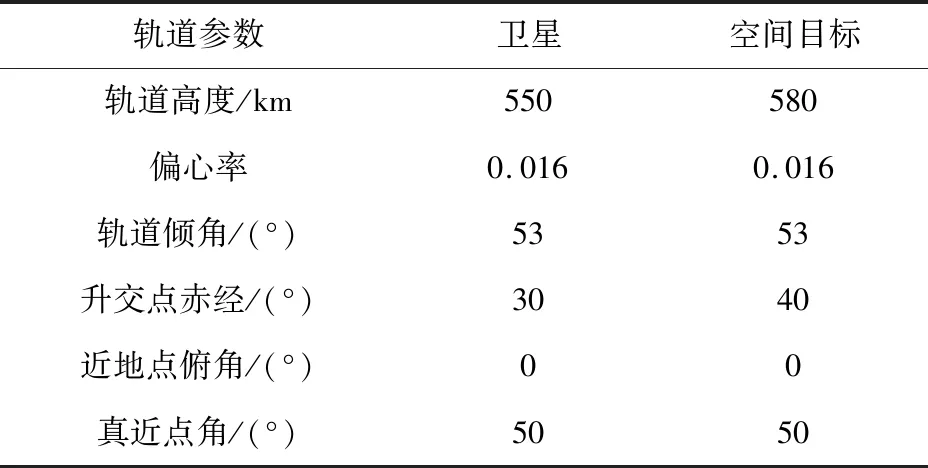
表1 轨道参数Table 1 Orbit parameters
其部分轨迹如图5所示,图中蓝色表示卫星轨迹,黑色表示目标轨迹,且此时目标未进入星敏感器视野,红色表示目标进入星敏感器视野时在空间中的轨迹.
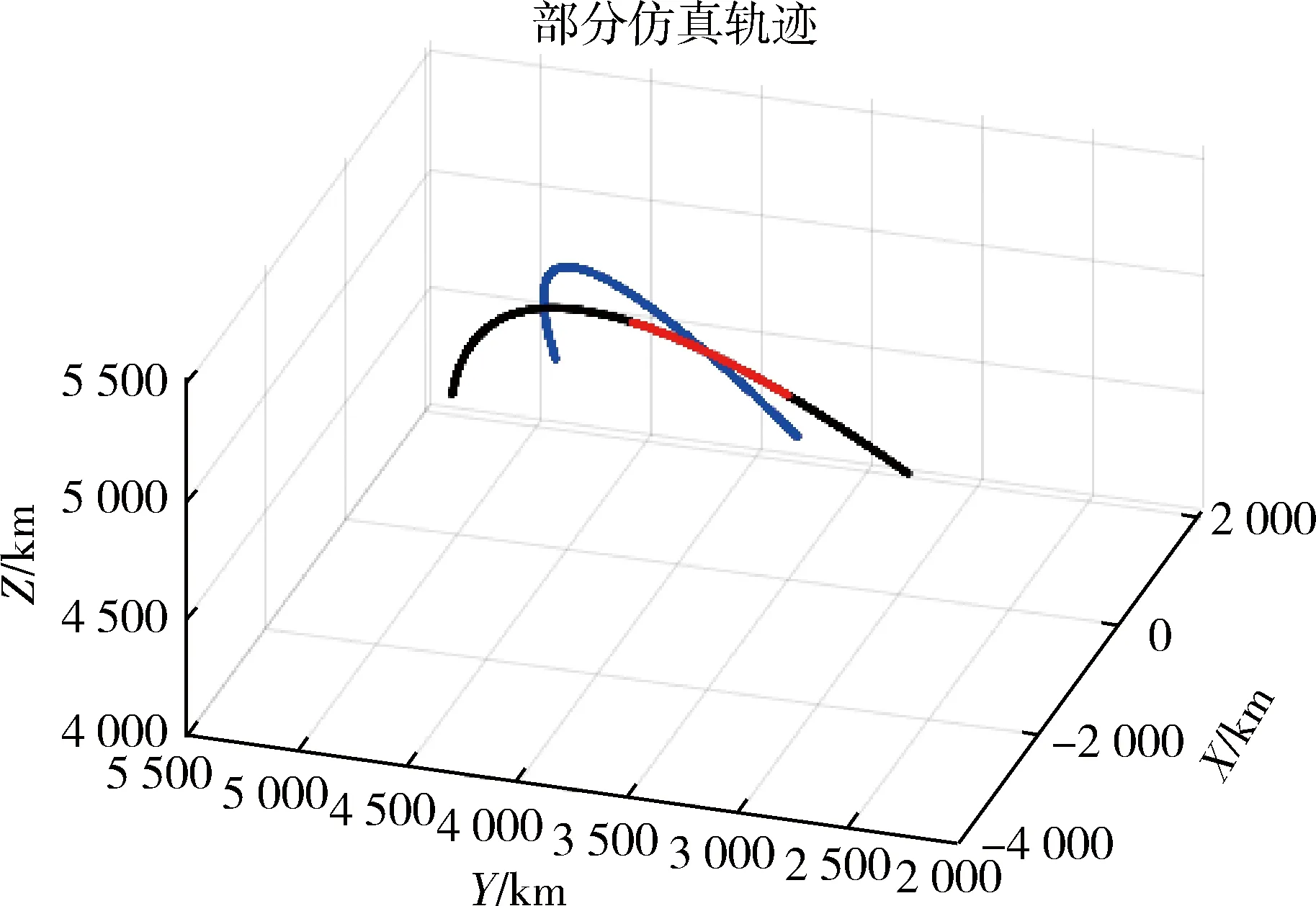
图5 部分仿真轨迹Fig.5 Partial simulation trajectory
使用图5中的轨迹仿真背景星图及目标,并使用本文的空间目标检测算法检测空间中的目标与理论值比较,其水平误差及垂直误差分别如图6(a)及(b)所示,图中黑色点表示误差,红色表示在该帧检测出的目标误差大于0.15°或无法确定目标.
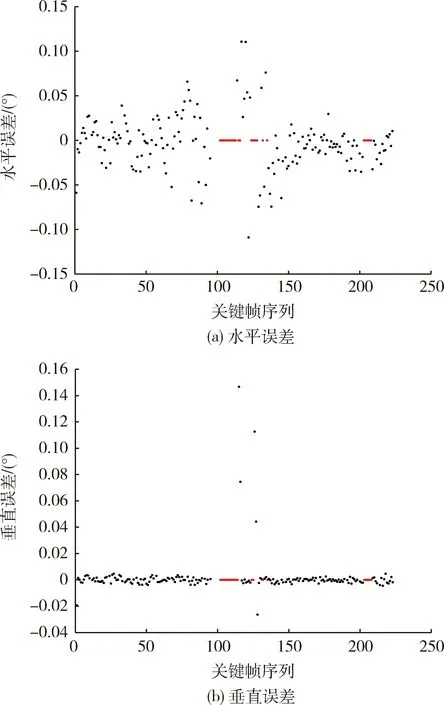
图6 目标检测误差Fig.6 Target detection error
由于图像预处理中星点质心细分定位算法的限制,图6中目标检测的水平误差及垂直误差小于0.15°的分别占到了关键帧中帧数的86.6%及88.6%,可用于初次对目标的检测.
利用STK的Astrogator模块搭建绕飞场景,仿真绕飞过程中卫星对目标的抵近[28].其中卫星轨道参数与表中的卫星轨道参数保持一致.在30~5 km抵近的过程中,卫星相对目标的位置变化如图7所示.
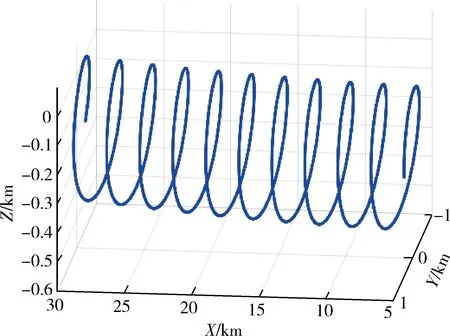
图7 卫星相对位置Fig.7 Relative position of the satellite
在卫星相对抵近过程中,使用本文中的目标检测算法检测目标并与理论值进行比较,其水平误差及垂直误差分别如图8(a)及(b)所示.
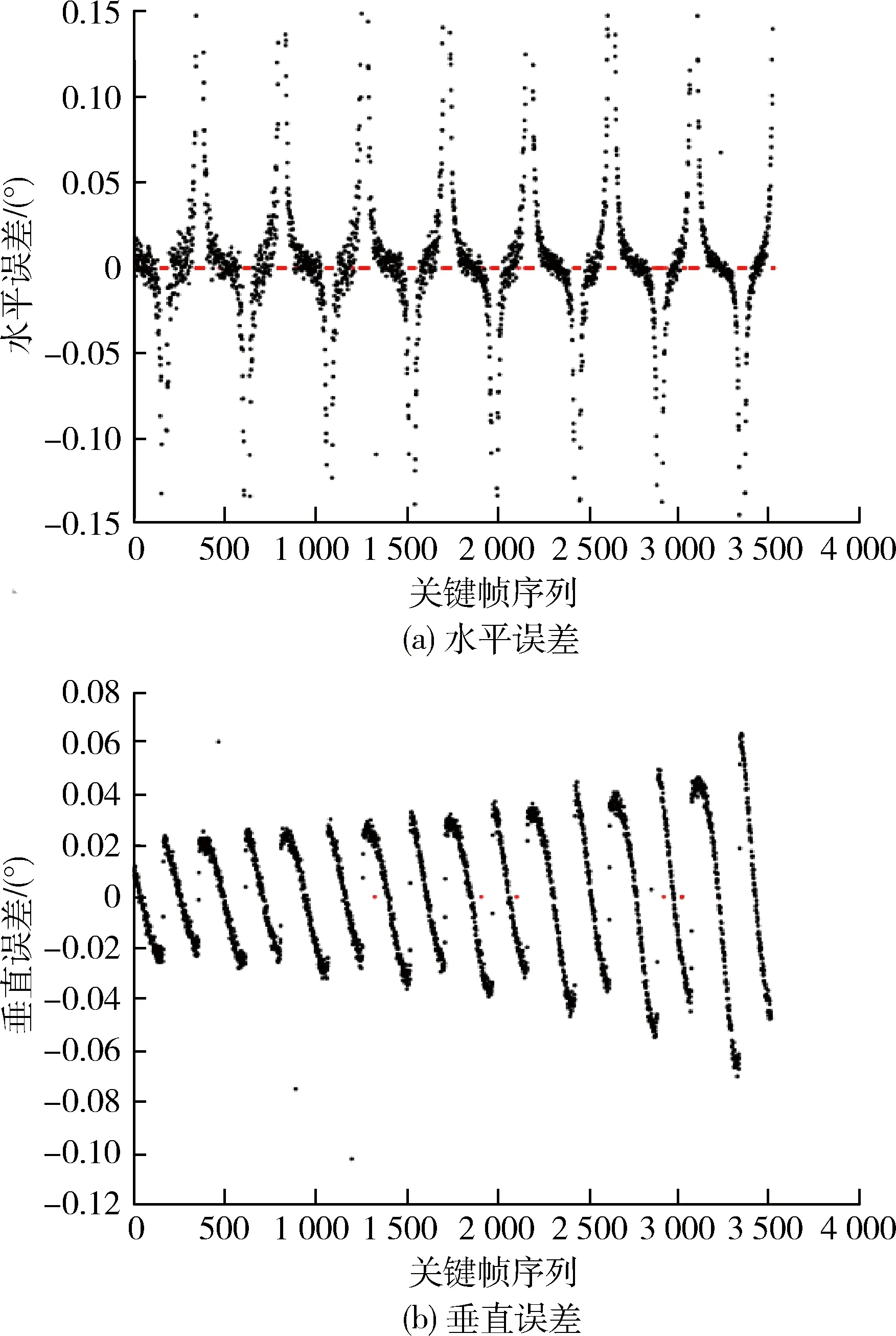
图8 抵近过程中目标检测误差Fig.8 Target detection error during approach
图中红色点表示此时误差大于0.15°或无法确定目标,相对抵近过程中,当目标离开或进入视野时会导致检测出的目标具有较大的误差,从而使得图中水平误差大于0.15°的帧重复出现.在抵近过程中,视野中的目标在垂直方向上变化范围逐渐变大从而形成了图8(b)中的误差变化.在仿真抵近过程中目标检测的水平误差及垂直误差小于0.15°的帧数分别占到了85.4%以及99.6%.
3 结 论
本文提出了一种用于中远距离下仅测角相对导航的空间目标检测算法,从经过预处理后的星图中选择出用于检测目标的关键帧,使用经过改进的OPTICS聚类算法提取目标轨迹,文中分别给出了在空间中初次目标检测以及抵近两个不同阶段下的仿真结果,验证了算法的可行性.

