地球静止轨道混合推进三星库仑编队队形保持控制研究

贺京九,袁长清,左晨熠

空军航空大学，长春 130022

0 引 言

库仑力编队飞行[1](coulomb formation flying,CFF)是近些年来一种新兴的卫星编队技术，其基本思想是通过某种手段使卫星带电(如电子枪发射电子使卫星带正电荷)，在编队各卫星之间形成库仑力，再设计相应的控制规律，进而控制编队达到期望状态.

库仑编队技术相对传统编队技术具有明显优势，主要体现在控制精度高、控制能耗小、能源可再生、不产生羽流污染等方面.在卫星编队运行过程中，构型保持是一项关键技术，是编队完成既定任务的前提和保证.当编队卫星数量达到三颗及以上时，星间耦合问题使得动力学模型的建立难度大大提高，相应控制律设计也变得十分复杂.目前国内外研究相对多集中于二体编队，已有的三体编队研究选择对问题做适当简化，主要是通过预设共线或等边三角形等特殊构型降低分析难度，或者将编队设置在深空环境，排除外部摄动干扰.黄静[2]在其博士论文中考虑输入有界与状态约束，设计了不同的反馈控制律，对于深空环境下的多体间相对距离控制问题有较好的表现.王景伟[3]详细分析了两星编队的稳定性与控制问题，提出基于PD控制的反馈控制律，分别实现了两种不同方向上的编队在小扰动下的构型保持.王有亮[4]基于平均化思想，推导了平均相对速度和脉冲速度增量之间的解析表达式，提出一种只需要星间测距信息的解析控制策略.朱数一[5]采用最优滑模控制方法，对于高精度精密编队构型维持问题取得了较好的效果.PETER等[6]分析了共线旋转三星库仑编队的面外稳定性，设计了非线性控制器消除了面外扰动的影响.QI等[7]提出了库仑双金字塔绳系构型，通过拉格朗日方程得到编队的运动方程，在卫星个数较少的情况下获得了单个星电荷解析解.史小平等[8]针对编队飞行动力学中的未知部分，提出采用自适应神经滑模控制律进行补偿.HOGAN等[9]研究了共线三星库仑编队的形状不变条件，并求出了相应的电荷解.林明培等[10]提出了库仑编队的八电荷对称构型，并利用中心流形约化和庞加莱映射研究了它的动力学特性.孙云龙等[11]研究了地球同步轨道处径向共线四星库仑编队的动力学与控制问题，设计了改进的LQR控制器，有效维持了编队构型.翟光等[12]讨论了圆轨道自旋绳系编队的控制问题，提出了一种非线性干扰观测器，在此基础上设计了控制律，并分析了其与几个重要参数之间的关系.

受空间摄动影响，卫星实际轨道会与参考轨道产生偏差，此时需要卫星机动对偏差进行修正.在实际任务中，很多机动需要大幅度转向，但由于库仑力是编队内部力，并不能改变卫星惯性轴的角动量.而且库仑编队的动力学模型是具有高度耦合的非线性模型，使得单纯依靠静电库仑力无法满足推进需求[13].为克服此缺陷，考虑在库仑力外加入电推力作为补充，改善库仑力编队的可控性，提高响应速率.等离子推进器是电推进技术的一种，其主要技术优点有比冲高、总冲量大、寿命长、体积小等.NASA开发的“渐进式氙离子推进器”(NASA’s evolutionary xenon thruster，NEXT)比冲大于4000 s，最大推力超过200 mN[14]，总冲量达107N·s量级[15].以上技术指标非常适合用于库仑编队中的推力补充.

本文研究了混合推进三星编队在地球静止轨道处的队形保持控制问题.通过假设三星始终处于共线分布对问题进行简化.考虑摄动影响，建立了混合推进三星库仑编队动力学方程，设计了投影圆轨道旋转编队构型，采用滑模控制方法设计控制器对环绕星进行队形保持控制，并进行了数值仿真验证.

1 动力学模型

设编队位于地球静止轨道(GEO)处，3颗星在任意时刻始终呈共线分布，中间位置为参考星，沿GEO绕地球转动，其余两星为环绕星，在编队构型平面内绕参考星转动,编队构型如图1所示.以参考星质心位置为原点建立Hill坐标系，编队质心与参考星质心重合.记两颗环绕星分别为Sat1和Sat2，参考星为Sat3，ri(i=1,2)为库仑力编队中第i个卫星在地心惯性坐标系中的位置矢量，r3表示编队质心在惯性系中的位置矢量，则第i个卫星相对于编队质心的位置矢量可以表示为ρi=ri-r3=[xiyizi]T，考虑摄动影响，Hill坐标系下的混合推进卫星编队动力学方程为

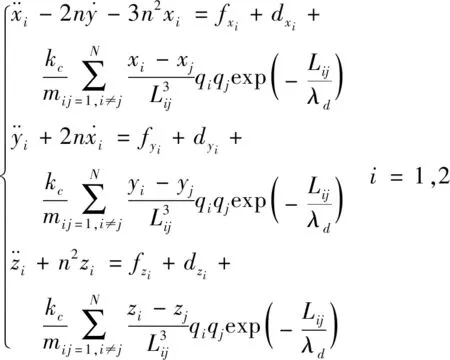
(1)

2 编队构型设计

当式(1)等号右端全部为零时，可以得到相对运动方程解析解：

(2)

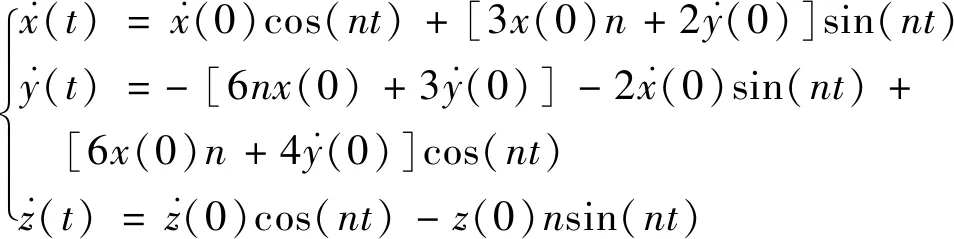
(3)

(4)

其中

(5)

(6)

当满足下列条件时，相对运动轨迹在Hill坐标系x-y面内投影是以原点为圆心的正圆：

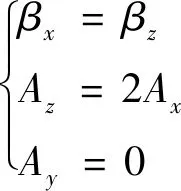
(7)

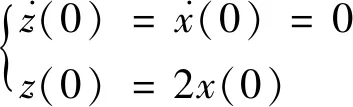
(8)

式(8)即为环绕星期望相对运动轨迹，在Hill坐标系x-y面内有y2(t)+z2(t)=[2|x(0)|]2，圆心(0,0)，半径R=2|x(0)|.记x(0)>0为环绕星Sat1轨迹，x(0)<0为环绕星Sat2轨迹，二者关于原点对称并绕其旋转.

3 滑模控制器设计

控制目标为Sat1和Sat2相对Sat3沿式(8)给定的期望轨迹运行，初始时刻存在位置误差e，考虑未知有界相对摄动的影响，设计滑模变结构控制器，以电荷积Q和电推力fet作为控制输入，Sat1和Sat2的相对位置为输出，通过调节输入使Sat1、Sat2获得适当的控制加速度，以期在有限时间内使e→0，实现编队期望队形的保持.

将式(1)改写成如下形式：

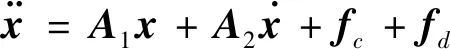
(9)

其中x=[x1y1z1x2y2z2]T，fd=[dx1dy1dz1dx2dy2dz2]T，

环绕星Sat1和Sat2相对参考星Sat3的期望位置在Hill坐标系下表示为xd=[x1dy1dz1dx2dy2dz2d]T，误差e=x-xd，求二阶导数得

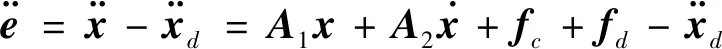
(10)

采用线性滑模面

(11)

其中，λ为六阶正定对称矩阵，s为6×1列向量.采用指数趋近律：

(12)

其中，ε、k为六阶正定对角矩阵，sgn(s)=[sgn(s1) sgn(s2) sgn(s3) sgn(s4) sgn(s5) sgn(s6)]T，对式(11)求导，与式(10)、(12)联立得

(13)

整理得

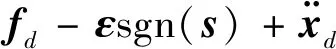
(14)

需要指出的是，式(14)中由滑模控制器求得的控制量fc为环绕星应产生的总的控制加速度，而该控制加速度由编队内部库仑力和环绕星上电推进力矢量和得到，因此得到控制加速度后，须将其转换为直接控制量Q和fet，为此将fc展开成如下形式：

fc=AQ+fet

(15)

其中Q=[Q12Q13Q23]T，A为系数矩阵

fet=[fx1fy1fz1fx2fy2fz2]T为电推进力，电荷积由最小二乘法[11]解得Q=(ATA)-1ATfc，库仑力大小为Fcou=miAQ，电推进力fet=mi[fc-AQ].

定义Lyapunov函数

(16)

求导，代入式(14)得

sT(-εsgn(s)-ks)≤-sTks≤0

(17)

故根据Lyapunov稳定性理论，系统全局渐近稳定，但实现过程中存在抖振.为了消除抖振影响，将符号函数替换成饱和函数，替换后的控制器如下：

(18)

其中，sat(s,Δ)=[sat(s1,Δ)sat(s2,Δ)sat(s3,Δ)sat(s4,Δ)sat(s5,Δ)sat(s6,Δ)]T[17]，饱和函数sat(si,Δ)具体构造为：

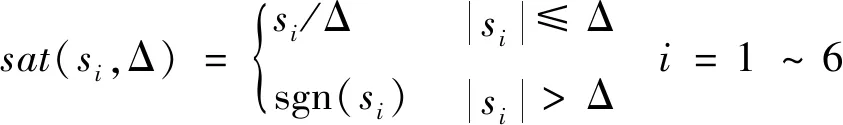
(19)

式(19)中Δ为消抖界宽.

4 仿真算例

本文选取地球静止轨道处卫星编队作为仿真验证对象，此处空间摄动影响主要有地球非球形摄动和日月引力摄动，用余弦函数表示为[18]

fd=diag{0.5 -0.5 0.5 0.5 -0.5 0.5}×

cosnt×10-5m/s2

参考星轨道为R=42164 km的圆轨道，角速度n=7.272×10-5rad/s.取|x(0)|=100 m，则环绕星Sat1和Sat2的期望相对运动轨迹为：

(20)

(21)

设环绕星质量为m1=m2=200 kg，在机动过程中同时使用库仑力和电推力构成混合推力进行轨道控制.控制参数选取如下：

λ=diag{3 3 3 3 3 3}×10-3，

k=diag{6 6 6 6 6 6}×10-3，

ε=diag{1 1 1 1 1 1}×10-4，

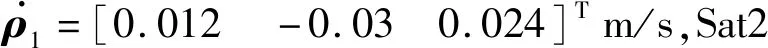
图1 编队示意图Fig.1 Formation demonstration

图2 星1位置跟踪曲线Fig.2 Position track of Sat1

图3 星2位置跟踪曲线Fig.3 Position track of Sat2

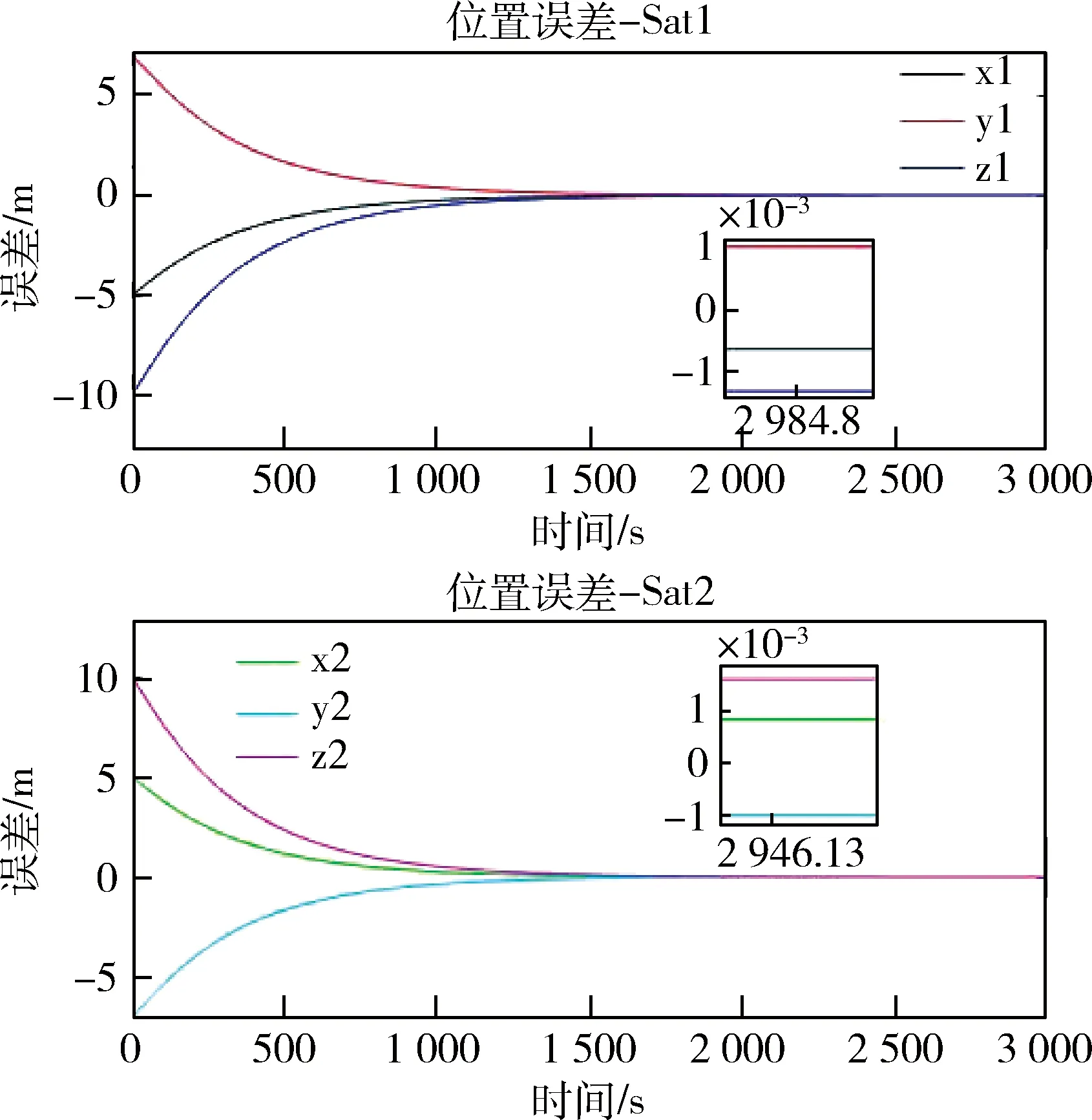
图4 环绕星位置误差曲线Fig.4 Position errors of follower satellite

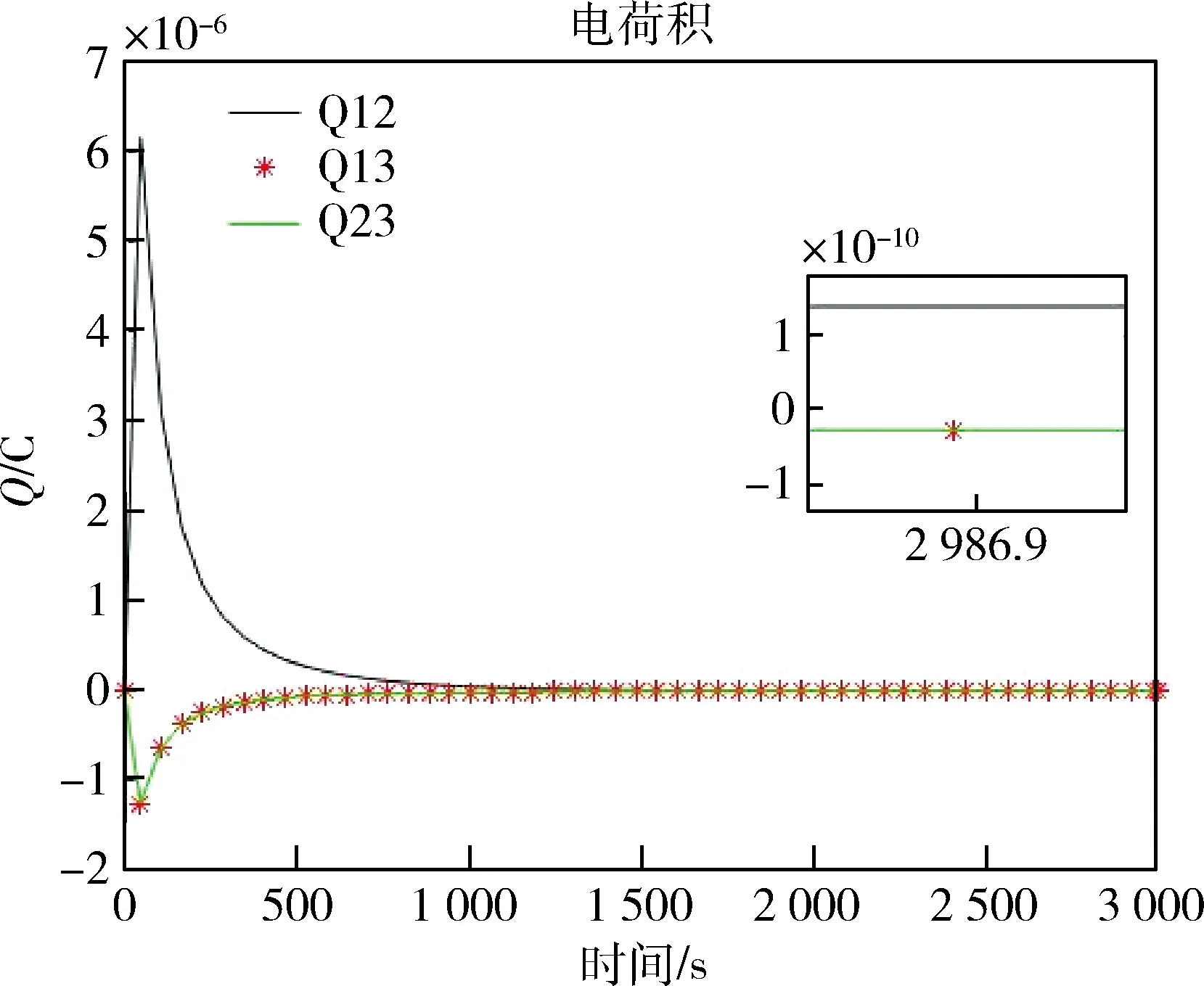
图5 电荷积曲线Fig.5 Charges product

图2、图3分别为环绕星Sat1、Sat2的三轴位置跟踪情况，由图可知跟踪过程平滑，无超调无抖动，有较好的动态性能.由图4可得，相对位置误差在2000 s内就已收敛到较高精度，随后稳定在±1×10-3m量级，相对轨道为250 m左右量级，可以认为取得了较好的控制效果.图5为编队内卫星两两之间的电荷积曲线，由图可知，两颗环绕星电荷积始终为正值，任意一环绕星与参考星电荷积都为负值且相等，这表明在充电过程中，环绕星始终带同种等量电荷，而参考星与环绕星为异种电荷，在机动过程中电荷积量级较大，接近期望轨道后维持在较低水平.图6为环绕星电推力大小，在机动过程中由于需要转向，此时电推力数值较大，随后环绕星逐渐向期望轨道靠近，电推力逐渐减小，最终维持在1 mN左右.

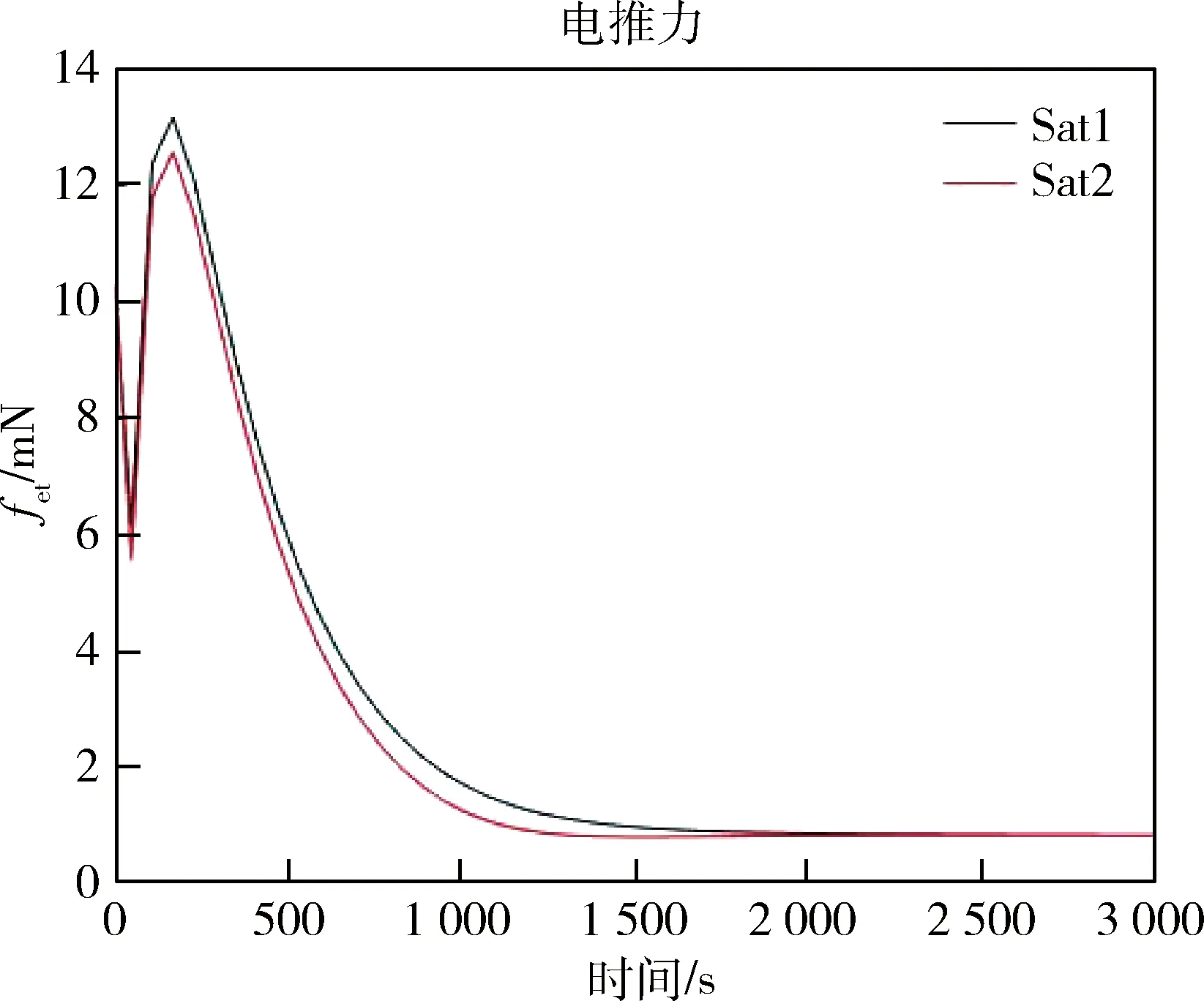
图6 电推力曲线Fig.6 Electronic thrust

5 结 论

本文基于相对运动解析解，设计了一种投影圆轨道旋转编队构型.考虑静止轨道处摄动影响，将其简化为有界量，采用指数趋近律设计了一种滑模控制器，用Lyapunov方法证明了其稳定性，通过控制电推力和库仑编队内部静电力实现对预设轨道的跟踪.仿真结果表明混合推力方案响应速度快，调节过程平滑，控制精度高，改善了仅依靠库仑力控制的缺陷，具有一定实用价值.