侧向微重力环境下板式表面张力贮箱内推进剂晃动行为分析

黄 滨，王 璐，陈 磊，刘锦涛，吴大转

1.浙江大学海洋学院，舟山 316021 2.北京控制工程研究所，北京 100190 3.浙江大学能源工程学院，杭州 310027

0 引 言

随着航天事业的迅速发展，对航天器的有效工作寿命与经济性有了更高的要求，因而推进剂在航天器中的填充量在不断地增大.现阶段的航天任务越来越复杂，对其姿态和机动性能要求越来越高，使得我们对航天器贮箱运行过程中推进剂在不同工况下的流动状态越来越重视[1-3].板式表面张力贮箱是国际上航行器主流的推进剂贮箱,它利用表面张力进行液体输送和气液分离，为发动机或推力器提供不夹气的推进剂，PMD作为板式表面张力贮箱的核心部件对贮箱为发动机或推进器提供不夹气的推进剂有关键作用[4-7].由于贮箱内推进剂的晃动会对PMD的液体管理能力产生重要影响，从而对航天器的正常运行产生重大影响，因此需要关注航天器飞行过程中不同姿态下的推进剂晃动问题[8-12].针对微重力环境下板式贮箱内流体行为研究，由于无法长时间进行地面微重力验证试验，常采用数值仿真进行先验性分析.通过数值仿真可以对航天器航行中推进剂行为进行预测，分析贮箱结构对推进剂管理性能的影响，对PMD结构设计与优化起导向作用[13-14].本文根据卫星可能的在轨飞行情况，针对重定位过程中推进剂有明显晃动产生的东西位置保持和南北位置保持工况下的板式表面张力贮箱内部流体运动过程进行数值仿真，并对贮箱内推进剂晃动行为和PMD液体管理性能进行分析，为后续微重力落塔试验及空间站试验提供参考.

1 数值模拟模型

本文采用VOF两相流动模型模拟侧向加速度环境下板式表面张力贮箱内流体分布规律，对贮箱内推进剂晃动现象进行分析研究，验证板式表面张力贮箱的推进剂管理能力.

1.1 VOF计算模型

VOF两相流模型是一种求解气液两相流动和自由表面流动的算法，它最早是由美国Los Alamos科学实验室开发用于处理含有自由面的二维粘性流体的数值计算方法[15-20].该模型通过预测气液两相界面的自由表面流动来监测侧向微重力 环境下贮箱内流体运动过程，由于推进剂在贮箱内的流动过程雷诺数较小，流动形态一般为层流，此种情况下VOF模型的基本方程式由物性方程、连续方程、动量方程等三类方程组成.

1)物性方程

流体的物性是由流体中不同相的体积组分确定的，物性方程就是要确定不同体积组分时流体物性的表达式，提供给其他输运方程.贮箱内部流动只有气液两相，假设第二相的体积组分被跟踪，那么流体的密度属性方程为

ρ=α1ρ1+α2ρ2

(1)

α1+α2=1

(2)

式中，ρ为混合流体的密度，α1、α2分别为第一相和第二相的体积组分；ρ1、ρ2分别为第一相和第二相的密度，它们为给定值.

2)连续方程

流体连续方程的基本表达式如下：

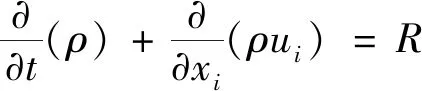
(3)

式中，ui为混合流体速度，xi为混合流体位置，R为源项.

3)动量方程

混合流体的动量方程为

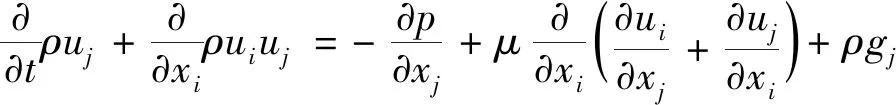
(4)

式中，p为贮箱压力，ui、uj分别为两相混合流体的气相和液相速度，xi、xj分别为两相混合流体的气相和液相位置，t为时间，gj为微重力加速度，μ为粘性系数.由于表面张力的作用，有

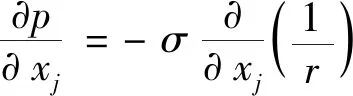
(5)

式中，σ为表面张力系数，r为液带的曲率半径，将式(5)代入(4)得混合流体的动量方程表达式

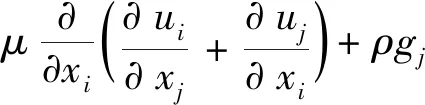
(6)

这就是混合流体的动量方程.

1.2 贮箱模型

以容积为884 L，内直径为1128 mm的板式表面张力贮箱作为研究对象，贮箱的PMD部件主要由4个导流板和1个蓄液器构成，结构简图1所示.贮箱轴向为Y轴，导流板布置在+X、-X、+Z、-Z四个方向上起到传输推进剂的作用，蓄液器位于贮箱下方出口处起到蓄液的功能.

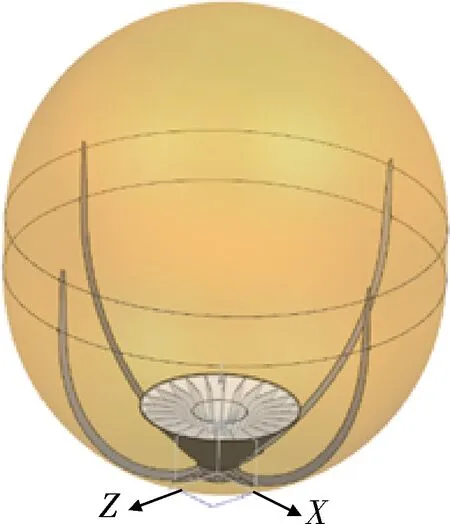
图1 板式表面张力贮箱三维模型Fig.1 Model of the vane-type surface tension tank

在ICEM中采用六面体结构化网格分别对贮箱和蓄液器进行计算域离散.为便于进行网格划分，对于贮箱和导流板区域采用1/4周期性流域进行网格划分；对于蓄液器区域采用1/24周期性流域进行网格划分.将周期性流域在ICEM中阵列出全域模型如图2所示，贮箱壳体和导流板流域总体网格数约为291万，蓄液器流域总体网格数约为309万，经过网格无关性验证，具有良好的收敛性，计算模型如图2中(c)图所示.

图2 贮箱各部件网格Fig.2 Mesh of components of the vane-type surface tension tank

1.3 模拟求解方案

(1)边界条件

计算时将各个壁面设为固壁边界，即为无穿透、无滑移边界.

(2)初始体积组分

计算域由液体和气体两部分组成，设定气相为主相，液相为次相.液体介质为NTO，密度为1444 kg/m3(20℃)，粘性系数为4.2×10-4Pa·S；气体介质为氦气，密度为0.1625 kg/m3(20℃)，粘性系数为1.99×10-5Pa·S.NTO的表面张力系数为0.026 N/m.在进行计算时需设定计算域内的初始体积组分分布，本文按照推进剂的填充比(容量占整个体积的比率)5%、25%、45%、60%，初始时推进剂处于贮箱底部进行设置.

(3)计算模型

利用 Fluent18.0进行一阶隐式非稳态数值计算，时间步长为 1×10-3s.压力-速度耦合方法采用PISO，其他方程的离散格式设置如下：压力离散：Body Force Weighted；动量离散：QUICK，体积分数离散：Compressive.方程收敛标准：质量守恒方程残差 RRR<10-3，所有速度量残差：RRR<10-3.能量残差RRR<10-3.

2 流体行为数值仿真结果与分析

侧向加速度环境模拟了航行器航行于东西位置保持和南北位置保持的工况下贮箱的受力情况，推进剂的初始液面处于贮箱底部，侧向加速度大小为0.015 m/s2，方向为X轴方向.

2.1 侧向微重力重定位数值仿真

通过数值仿真模拟侧向微重力重定位过程，得到推进剂重定位后的分布情况，预测了板式表面张力贮箱内推进剂在侧向加速环境下重定位过程中的流体行为.为了解不同推进剂填充比对重定位过程中推进剂晃动行为的影响，设定初始推进剂填充比分别为5%、25%、45%、60%.各填充比下贮箱初始气液云图如图3所示，重定位后贮箱气液分布如图4、图5所示.

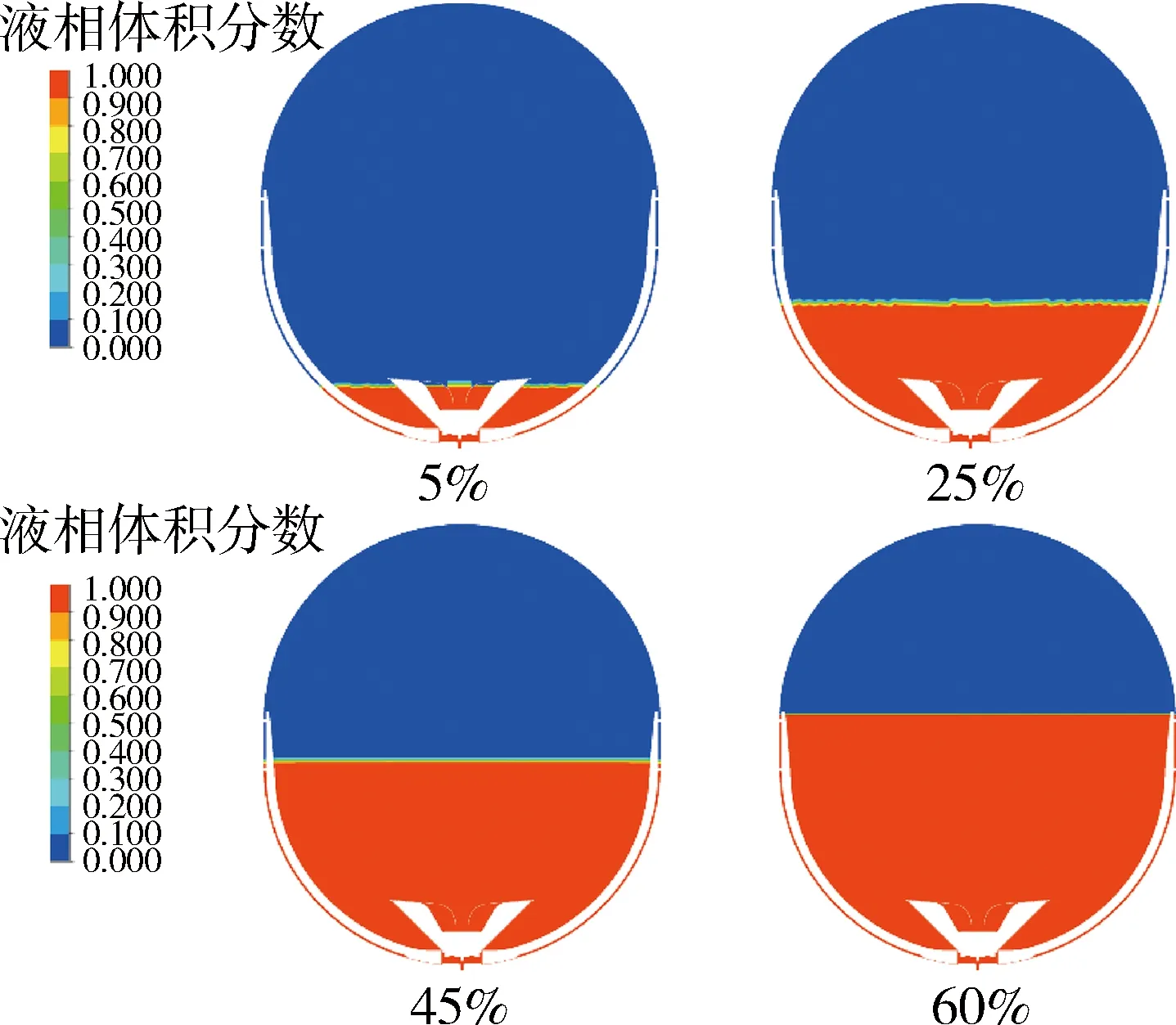
图3 各填充比初始气液云图Fig.3 Initial gas-liquid contours of different fill ratio

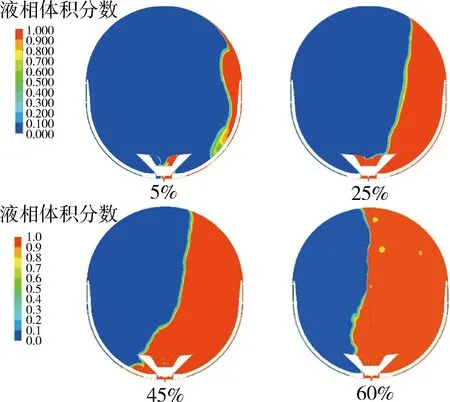
图4 各填充比重定位结束气液云图Fig.4 Gas-liquid contours after reorientation of different fill ratio

图5 各填充比重定位结束气液交界面Fig.5 Gas-liquid interface after reorientation of different fill ratio

重定位结束气液云图表明气体和液体在重定位过程中无混合，气液界面稳定后呈现波浪状，蓄液器内部液体未流失.气液界面呈现波浪状说明液体内部存在相互作用力使得液体内部产生晃动；但液体的晃动对气液分离过程并没有造成破坏、蓄液器仍能保持液体储蓄，表明该板式表面张力贮箱的PMD在该侧向加速的环境下能够实现推进剂的管理与运输.气液交界面图可以更清晰显示液体表面的波浪状，液体在侧向微重力的作用下将贮箱底部、中部、顶部的侧表面浸染.

2.2 重定位过程流量分析

为更清晰地了解板式贮箱侧向加速度下重定位过程中推进剂体运动过程，对板式贮箱初始气液交界面和竖直对称面进行流量监测，得到重定位过程中液体的晃动特性.流量监测面设置示意图如图6所示，流量监测曲线如图7、图8所示.

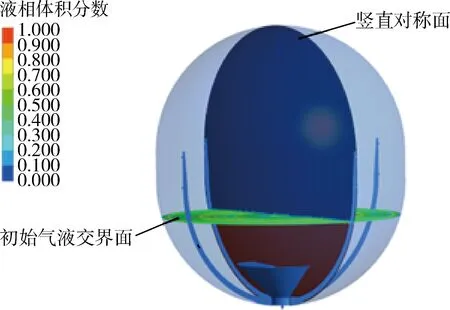
图6 流量监测面设置示意图Fig.6 Schematic diagram of flow monitoring surface setting

通过液体晃动气液云图周期变化可以更直观的对流量时间曲线的变化趋势进行解释，以填充比为25%时液体晃动周期图为例如图9、图10所示，并将气液云图对应的时刻点在相应的流量时间曲线上进行了标注如图7(b)和图8(b)所示.

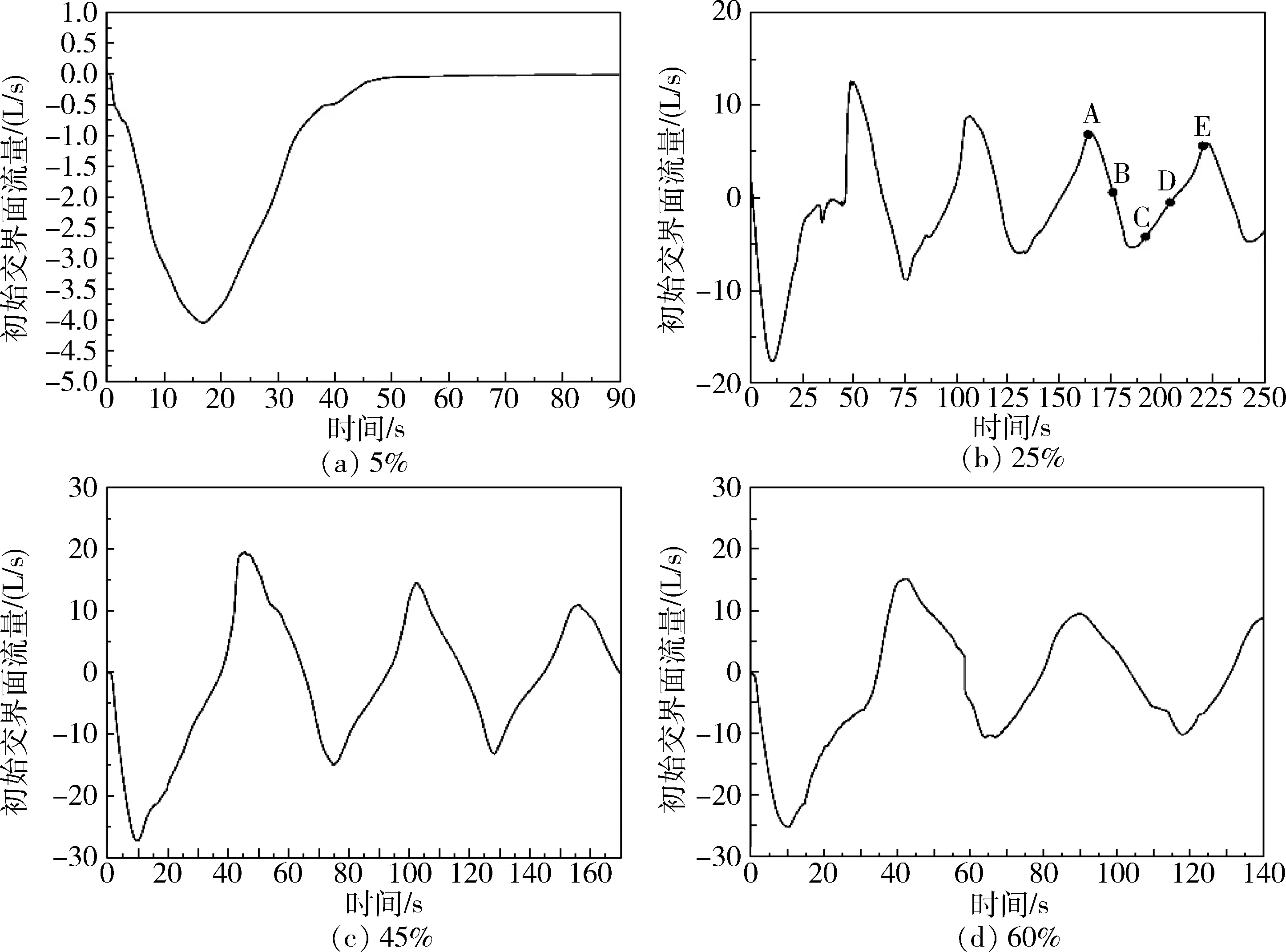
图7 各填充比交界面流量时间曲线Fig.7 Flow-time curve of interface flow of different fill ratio

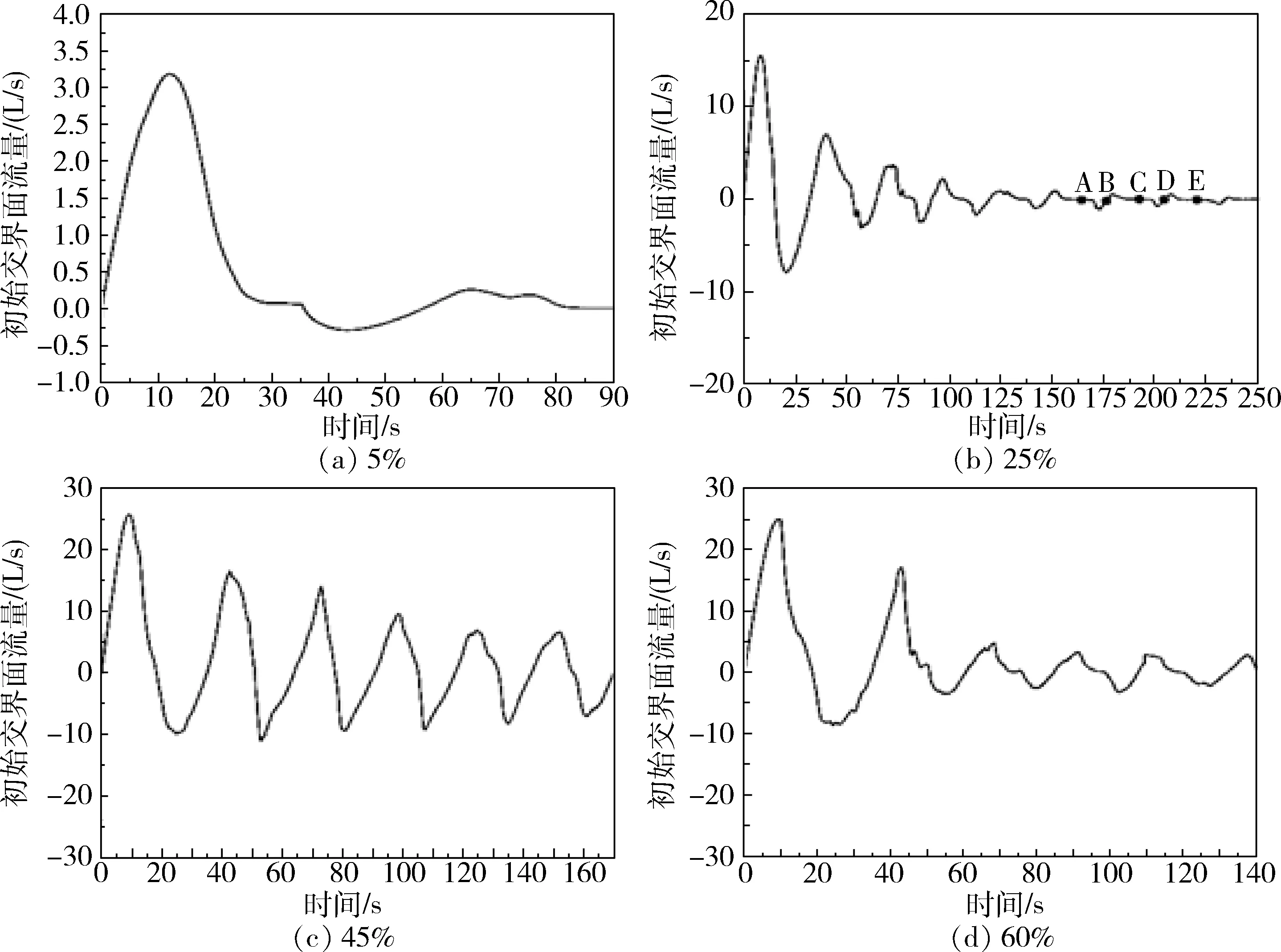
图8 各填充比垂直对称面流量时间曲线Fig.8 Flow-time curves of vertical symmetry plane flow with different fill ratio

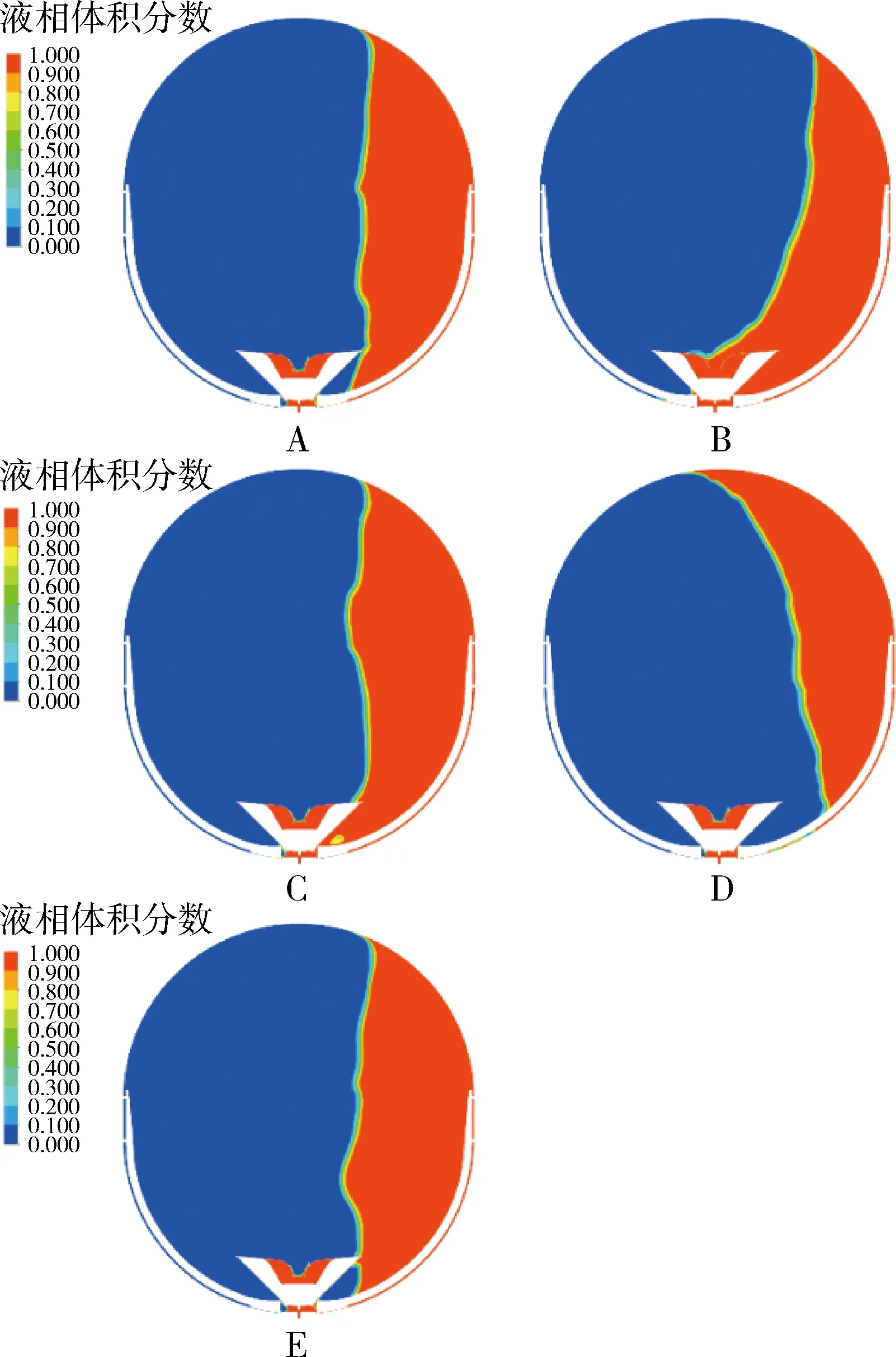
图9 填充比25%时液体晃动周期气液云图Fig.9 Gas-liquid contour of sloshing cycle of fill ratio 25%

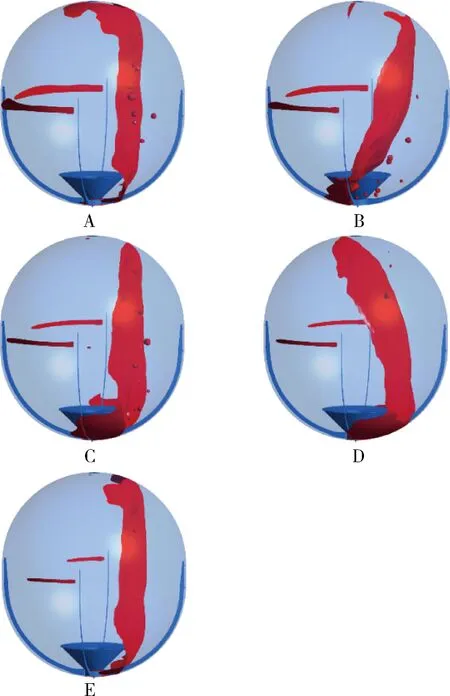
图10 填充比25%时液体晃动周期气液交界面Fig.10 Gas-liquid interface of sloshing cycle of fill ratio 25%

初始交界面和竖直对称面的流量时间曲线显示在重定位过程中流量的变化存在明显的波动，通过液体晃动周期气液云图可以更直观的看出液体的晃动行为.通过对比不同填充比的流量时间曲线发现：液体晃动程度与推进剂的填充比存在一定的联系.随着填充比的增加，重定位完成的时间与流量波动的最大幅值的变化呈现先增大后减小的趋势.该现象表明随填充比的增加液体的晃动剧烈程度呈抛物线状的变化趋势，且存在峰值状态，为保证贮箱的正常运行和PMD的推进剂管理能力，应在峰值区间内进行密集试验.

3 结 论

本文设置X轴方向0.015 m/s2的加速度环境模拟在轨飞行时东西位置保持和南北位置保持航行工况下的侧向微重力环境.对不同填充比表面张力板式贮箱重定位过程进行数值模拟，得到侧向微重力环境下重定位过程中推进剂的运动过程：气液在重定位过程中无混合且液体能够稳定积蓄在贮箱的一侧，蓄液器能够有效的储蓄推进剂，气液交界面呈波浪状.重定位结果表明该板式表面贮箱在该侧向微重力环境下可以有效地实现气液分离，虽然推进剂内部存在明显的晃动，但贮箱内PMD能够有效的管理贮箱内部液体.流量时间曲线显示贮箱内液体的晃动与液体的填充比存在一定的关联，在环境一定的情况下，重定位的时间和流量波动的最大幅值随流量的增加呈先增加后减小的趋势.本次模拟结果对板式表面张力贮箱的侧向加速度下的运行有了一定的预测，对后续即将开展的微重力落塔试验和空间站试验提供了重要的参考依据.