考虑实时电力交易的电动汽车群组充放电优化策略

黄敬尧，朱嘉帅,2，侯登旭，孟明梅

(1. 三峡大学电气与新能源学院，湖北 宜昌443002；2. 国网湖北省电力有限公司武汉供电公司，武汉430013；3. 国网湖北省电力有限公司孝感供电公司，湖北 孝感432100)

0 引言

随着新一轮电力体制改革的逐步深入，国家发改委提出2020年开始我国将逐步建立发用电双方带曲线交易的模式，电力市场实时交易覆盖面将进一步扩大[1 - 2]。同时，在政策与市场的双重驱动下电动汽车产销量不断增长，电动汽车入网技术(vehicle-to-grid，V2G)使其与电网紧密联系[3 - 4]，利用电动汽车作为储能装置[5]可以根据电力市场的实时价格波动，将富余的电能出售到电力市场“低买高卖”获取收益，同时减少电动汽车大规模接入电网带来的功率波动与负荷冲击问题[6]。

目前，大量学者对电动汽车的充放电优化进行了研究。文献[7 - 8]引入了虚拟同步机技术，实现了对微电网频率的无差调节，起到了减小负荷波动率、削峰填谷、降低经济成本的作用；文献[9]以换电模式作为电动汽车的能源供给模式，构建了基于排队论的换电站运行状态转移模型，实现了有序充电模型的快速求解。以上文献仅从技术层面论证了有序充放电的优势，未考虑增加用户的收益或减少用户的成本。

针对参与电力交易的电动汽车充放电优化开展了相关研究。文献[10]建立主从博弈模型，以主动配电网与电动汽车为对象，基于贪心策略进行两阶段优化，验证了充放电策略的经济性和有效性；文献[11]基于蒙特卡洛模拟和粒子群算法进行仿真计算，控制策略思路清晰，计算变量少；文献[12]考虑动力电池的损耗成本，采用迭代法对电池损耗成本和充电站的充放电计划进行联动优化，验证了电动公交车参与V2G时的优越性；文献[13]针对居民小区的个人用户，考虑了配电变压器供电容量限制，设计了求最优网格选取结果的方法与步骤，降低了用户成本，起到了削峰填谷的作用。但以上文献均通过分时电价作为减少用户成本的渠道，未考虑参加电力市场进行电力交易；文献[14]建立基于区块链的充电权交易机制与模型，需通过双向拍卖市场和P2P市场挂牌交易，使电动汽车所有人和电力市场之间的电力交易受到一定的约束，且不是根据实时曲线进行电力交易。

在上述背景下，本文针对商用电动汽车群组有序充放电问题，设计将电动汽车电池中储备的富余电能出售到电力市场中参加实时电力交易的电动汽车充放电优化策略。在保障电力系统安全的情况下，以电力交易收益和车辆运营收益最大化为目标，基于多目标决策理论建立优化模型，通过遗传算法求解。最后，基于新加坡能源市场计算用户收益并将该策略有序充电与无序充电情况进行对比，验证本策略的有效性。

1 电动汽车群组调度架构

1.1 电动汽车调度策略

本文提出的充放电优化策略适用的对象为商用电动汽车群组，以作为电动汽车群组运营主体的商业用户的收益最大化为导向。要增加电动汽车所有者的收益主要通过参与实时电力市场交易和优化电动汽车运营来实现：一方面，将电力市场的实时电价传递到电动汽车群组，在电动汽车群组有富余电能的情况下，将电能释放出来参与实时电力市场进行交易，实现“低买高卖”获取利润，同时也节省充电支出；另一方面，使电动汽车周转效率最大化，在相同情况下完成更多的业务，增加电动汽车的运行收益。

与此同时，为了保障电网系统的安全稳定运行，充电站的负荷不应超出电网的承受范围。因此，本文将讨论电网的安全约束条件，以确保不影响电网的安全运行。

1.2 智能充电站工作场景

电动汽车充电站的结构如图1所示。当电动汽车连接到电网时，可以将其看作一个储能装置。为便于电力市场和电动汽车间信息的交互，本文引入聚合器作为两者联系的桥梁[15]，同时发出指令对电动汽车的运营进行调度。商用电动汽车群组产权所有者为商业用户，聚合器及电网在内的设备产权所有者均为电网公司。

图1 电动汽车充电站结构图Fig.1 Structure of an electric vehicle charging station

1.3 电动汽车充放电流程

考虑到商用电动汽车群组用户的运行要求以及电动汽车是否有富余的电能参加电力交易，本文设计了如图2所示的充放电控制流程图。

图2 充放电控制流程图Fig.2 Charge and discharge control flowchart

2 多目标决策条件建模

2.1 经济收益建模

2.1.1 电力交易收益

电动汽车作为实时电力市场的参与者，可以为实际交易的电能收益或支出相应的能源费用。根据实际情况，电动汽车可以进行正调节或负调节：在正调节时，将能源费用支付给提供电动汽车所有者；在负调节时，参与者支付从电网获取的能源费用。提供负调节Wneg给电动汽车充电，其值受到之前用于驾驶的能量的限制：

(1)

式中：dd为当天行驶的路程，km；ηveh为功耗， kWh/km；ηcharge为充电效率。

通过将可用能量Wneg除以相应的调度时间tdisp,d(每辆电动汽车每天参与交易时间的平均值)可以求出负调节时每个电动汽车可以提供的功率Pneg。

(2)

电动汽车每天接通电源的时间tplug乘以能源消耗的概率，可以求出tdisp,d，这个概率可以通过Rd-c来估计，Rd-c是实际每天消耗的能源Edisp和潜在的合同能源Econtr之间的比率。

(3)

tdisp,d=Rd-ctplug

(4)

1辆车参与电力交易的最大有功功率Pmax受充电器容量PC和最大安全充电功率Pm的限制。

Pmax=min{Pc,Pm}

(5)

N辆电动汽车和T个时间段的每日总收益为：

(6)

式中：p(cap,j)为第j小时的容量价格；Pi为车辆i的充电功率；c(pe)j为第j小时的现货市场能源价格；p(el)j为第j小时的规定能源价格；E(disp)i,j为第j小时的车辆i的分解能量；ton,i为车辆i接通电源的时刻；tplug,i为车辆i接通电源的时长。

2.1.2 车辆运营收益

在电动汽车连接充电站进行充放电时，无法进行正常运营，过多的电动汽车连接到充电站，势必会影响到商业用户的正常运营。对运营的影响程度本文用运营影响系数来表达，以研究对正常运营影响最小的情况。

为便于分析，本文规定电动汽车到达和离开充电站的时间是固定的，电动汽车群组所有者通过估计业务出现的时刻和业务处理时长来使业务等待时间最小化，推荐的车辆参数可以从排队论中定义的M/M/s模型获取[16]。则所有n辆车都可用的概率p0为：

(7)

式中：s为电动汽车的数量；λ为每个时间单位的预期干预次数；μ为每个时间单位内完成的预期干预次数。

系统中存在n个业务需要处理的概率pn为：

(8)

系统中每辆电动汽车的预期业务数量L如下：

(9)

将等待时间用W表示，在稳态排队过程中每辆电动汽车的预期业务数量为：

L=λW

(10)

(11)

为了更加直观地以使用经济性来评估调度结果，本节将运营影响系数用经济指标进行了相应转化。假定完成一个业务的收益为c0，则商用电动汽车用户的总收益C为：

(12)

式中N为电动汽车的数量。

基于需要处理的业务可以等待的最长时间spref,j=f(Wmax)，可以计算满足条件的当前可用车辆数的最小值。一定数量的可用车辆能保证车辆运营收益C最大，有：

(13)

式中：spref,j为每小时首选车辆数量，使用N辆电动汽车和T个时间段，通过最小化与该值的偏差进行单准则优化。

2.2 电力系统安全约束

2.2.1 电力容量约束

在本文提出的电动汽车充放电策略中，智能充电站内有聚合器，根据单辆电动汽车的耗电量计算出每个小时的总充电需求，即为充电站每小时需要提供的电能。为了保障电力系统的安全稳定运行，充电站所能提供的电能不应超过充电站的最大容量，充电约束关系为：

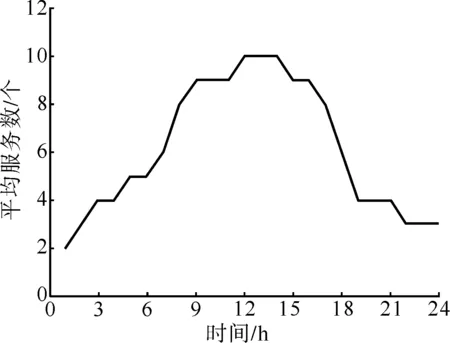
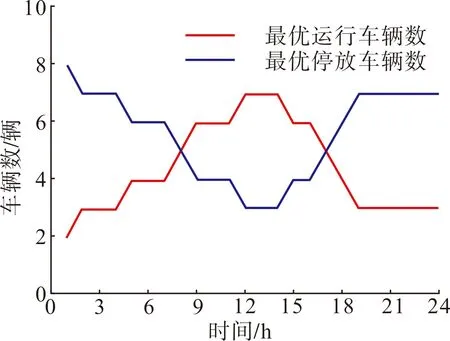
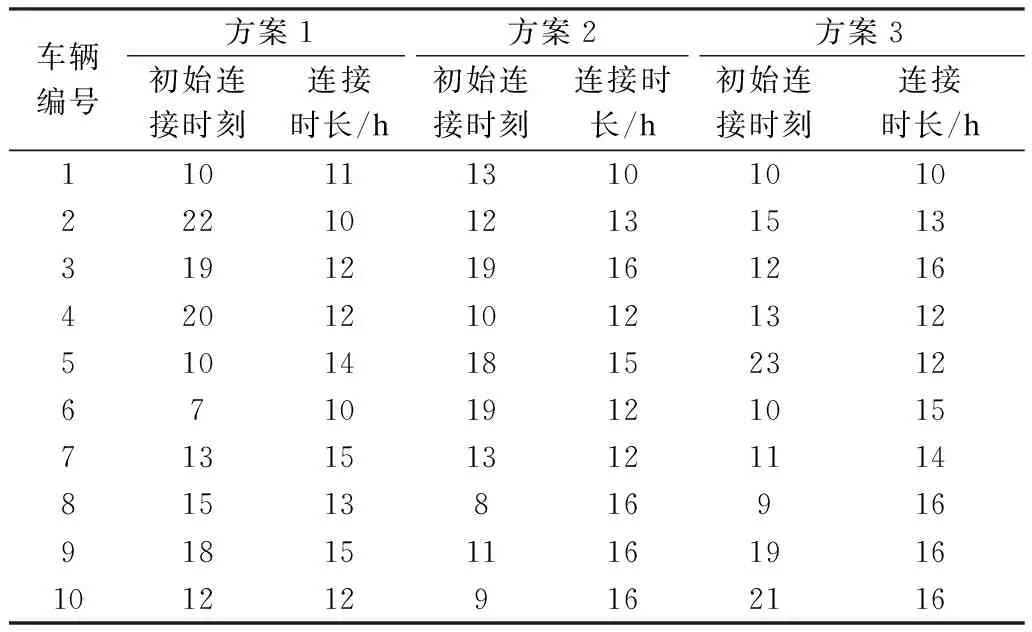
0

(14)

式中：pt为t时刻电网负荷的预测值：pmax为充电站所能提供的最大充电功率：τ为充电站的充电效率。

2.2.2 电池容量约束

本文将电动汽车的电池作为储能设施建模，其容量等于充电站中所有电动汽车电池容量的总和。总容量会随着时间的变化而变化，因为停车场中可用的电动汽车数量是变化的。下面两式分别表示停车场储能设施在t小时的最大容量和最小容量。

(15)

(16)

得到充电站电动汽车电池总容量的最大值和最小值，则电动汽车参与实时电力交易的容量如式(17)所示。

(17)

式中Et为电动汽车参与实时电力交易的容量。

充电功率可以通过减载装置进行降低，即车辆连接后不立即开始充电，而是通过聚合器结合电力市场实时电价和商业运营的要求，在满足车辆正常运行及不超过充电设施最大功率限制的前提下，再进行针对性充放电。

3 优化模型求解

3.1 多属性效用理论

多属性效用理论定义了多属性效用的结果，它是各个属性的效用函数。多属性效用理论规定了几种可能的函数以及每种函数的适用条件。如果存在相互独立效用，则多属性效用函数如式(18)所示。

(18)

式中：ui(xi)为属性i的单属性效用值，其值为xi(xi范围为0～1)；ki为属性i的权衡参数；K为归一化常数。

如果给定X2=x2时X1的随机变量的结果不取决于x2的水平，则属性X1的效用独立于X2。如果满足累加条件独立性(更严格的偏好条件)，则偏好由边际决定，而不是由每个绩效指标的联合分布决定。

如果存在累加条件独立性，则多属性效用函数具有累加性，如式(19)所示。

(19)

(20)

总体效用函数可以反映各个标准之间的3种不同类型的关系。本文使用多属性效用理论进行优化，该理论允许决策者对风险采取不同的态度：在补偿情况下，可以通过一项标准的执行弥补另一项标准的不足，如式(21)(a)中所示；在累加情况下，一个标准的执行与其他标准的值无关，如式(21)(b)中所示；在互补情况下，通过一项标准获得最优结果是首要目标，如式(21)(c)中所示。

(21)

可以根据决策者的多元风险状况来区分这3种情况。第1种情况代表风险规避，第2种情况代表风险中等，第3种情况代表风险寻求。在本文确定函数的方法中使用的方法是通过每个u(x)确定kj的值，并进行迭代求解找到K值。

(22)

3.2 多目标优化

通常有两种方法生成多目标优化的解集：标量化和非标量化方法。标量化方法明确地使用标量化函数将问题转换成单目标问题，也是本文所采用的方法。调度优化首先对先前分析的电力交易收入函数和车辆运营收入函数进行单目标优化，该优化输出的是基于电力交易收益UR和车辆运营收益UC的单一最大值的效用函数。接下来，将多属性效用理论应用于聚合效用来执行多目标优化，分别如式(23)—(24)所示。

(23)

(24)

式中：R(x)为电力交易收益；C(x)为车辆运营收益。

多目标优化函数为：

(25)

式中：K为归一化常数；k1和k2分别为电力交易收益和车辆运营收益的权衡参数。

在本文中，将使用非线性(25)和加性模型效用函数(26)：

U=k1UR+k2UC

(26)

优化问题是对偶的，有两种解决方法。一种需要找到由二进制变量组成的矩阵，另一种仅需找到整数变量。本文采用后一种方法，从而大大减少了变量数量，并将优化问题设置为混合整数非线性规划问题。优化函数是非线性的，具有式(27)所示的线性约束。

(27)

式中：T(min,on),i和T(max,on),i分别为车辆i的最早和最晚连接时刻；T(min,plug),i和T(max,plug),i分别为车辆i的最短和最长连接时长；Pi,max为车辆i的最大充电功率。

第1个约束将车辆活动限制在1天内(24 h)，第2个约束给出了决策者允许车辆停放而不使用的时间范围。可能的堵车时间范围由第3个约束条件设定，每辆车的最短和最长连接时长如式(28)所示。

(28)

式中：Wi为车辆i的等待时间；Rd-c为每天实际消耗的能源和潜在的合同能源间的比率；Pmax,i为车辆i所连接充电桩的最大功率；Tservice,i为车辆的预期运营时间。

最后，每个车辆的最大充电功率由第4个约束给出。

由于根据不同的运营情况，电动汽车的使用时间是随机的。因此，白天行驶的公里数范围是应用M/M/s模型进行运营的泊松概率分布的结果。

(29)

式中μ为每个时间单位内完成的预期干预次数。

接下来，使用遗传算法解决优化问题。首先确定每个条件的效用函数，然后将多属性方法用于车辆调度。完整的优化过程如图3所示。

图3 优化过程图Fig.3 Optimization process diagram

4 仿真算例分析4.1 参数设置

本文以某充电站为例，研究优化电动汽车调度的方法，假设其拥有10辆电动汽车组成的小型电动汽车群组。电动汽车的运行业务以M/M/s模型建模，一辆车每小时平均已完成业务μ=2， 允许的最大等待时间Wmax=30 min。通过3.1节可知，最佳的未运营车辆数量spref(t)和运营车辆数量N-spref(t)。其中，该电动汽车每千米耗电参数dd=0.15 kWh/km，充电效率ηcharge=0.95。

图4中给出了1天中各时段的平均业务数λ(t)，图5给出了最优的运行和停放车辆数量。

图4 各时段平均业务图Fig.4 Average service graph during every period

图5 最优运行和停放车辆图Fig.5 Optimal operation and parking of vehicles diagram

利用每辆车进行运营的泊松分布，求出每辆车在运行时间内已完成任务的概率分布。接着将概率分布离散化，以便获得每辆车的实际业务数量，M/M/s模型应用程序的最终结果是每辆车的预期千米数。车辆充电参数见表1，计算参数见表2。

表1 输入充电参数Tab.1 Input charging parameters

表2 单目标优化的第一步优化结果Tab.2 First-step optimization results for single-objective optimization

本算例选择了新加坡能源市场公司2020年4月22日24 h实时价格进行计算[17]，如图6所示。

图6 新加坡电力市场能源价格Fig.6 Energy prices in electricity market of Singapore

4.2 各方案调度对比分析

根据前文提出的两步法，首先对电力交易收益和车辆运营收益函数在约束条件下执行单目标优化，然后构建效用函数优化目标。接下来使用遗传算法，对3种不同类型的目标函数执行多目标优化，具体取决于决策者的风险态度，3种方案的最佳调度安排见表3。

3种可能的情况反映了3.2节中的3种不同的决策策略：风险规避、风险中等和风险寻求。表5中列出了优化问题的最终结果和3种方案的情况。图7和图8分别是白天的计划充电功率和进行充电的电动汽车数量。

表3 针对3种方案的最佳调度Tab.3 Optimal scheduling for three scenarios

表4 3种方案下的最终结果Tab.4 Final results under the three schemes

图7 各时段计划充电功率Fig.7 Planned charging powers for each period

图8 各时段运行的电动汽车数量Fig.8 Numbers of electric vehicles running during each period

通过对优化得出的结果进行对比可知：方案1(风险规避)的综合效果最佳；方案2(风险中等)中某一方面的突出表现不及整体平衡重要，其综合效果不尽人意；方案3(风险寻求)中一个条件的执行不与其他条件的相关，但是由于各个条件的关联性较低，因此也能达到良好的总体效果。

优化结果同时得出，在选择方案1的情况下，每辆电动汽车每年的平均电力交易收益为425.17美元(约合人民币2 965.48元)，综合收益为人民币18 796.48元，具有一定的经济效益。

4.3 考虑有序充电的必要性

为了进一步研究本文充放电策略下电动汽车群组优化调度的效果，分别在无序充电与本策略有序充电的情况下，对拥有100辆电动汽车的中型商用电动汽车群组进行分析。图9是100辆电动汽车在两种情况下的日负荷曲线图。

图9 有序充电与无序充电的日负荷曲线图Fig.9 Daily load curves of ordered charging and disordered charging

由图9可知，使用本文充放电策略的优化调度降低了电动汽车大规模、集中性接入电网时的负荷冲击，起到了“削峰填谷”、错峰充电的作用，更加合理地配置了智能充电站的设施使用。

综上所述，运用补偿效用函数的方案一是最佳选择，其使得包含电力交易收益和车辆运营收益在内的总收益最大化，并且不会影响电网的安全稳定运行，与此同时还可以起到“削峰填谷”的有益作用。

5 结论

本文在新电改推进实时电力交易的背景下，基于电动汽车大规模商用的趋势，考虑到用户的需求和收益，以及电网的安全性，提出了一种参加实时电力市场交易的电动汽车的充放电策略。主要工作和得出的具体结论如下。

本文在电动汽车充放调度优化中，对实时电力交易收益、车辆运营收益以及充电设施安全约束进行建模，并使用多属性效用理论优化了该模型，最后通过算例验证了该模型。

商用电动汽车群组用户在参与电力市场带曲线实时交易中可以获得一定的收益，且商业用户的日常运营不会受到明显影响，同时对电网的安全性也不会造成影响。另外，通过在本策略下进行有序充电和无序充电进行对比，证明本策略可以起到“削峰填谷”的作用，缓解了电网“负荷尖峰”的问题。