DFIG网侧变换器反馈线性化与滑模控制

侯传羽，李岚，赵楠，杨琦，杨旭

(太原理工大学电气与动力工程学院，太原030024)

0 引言

随着近年来风能设施的进步，风能作为可再生能源，愈来愈具有经济竞争力和发展潜力[1 - 3]。而目前主流的风电机组通常采用变速恒频机组，以双馈异步发电机(doubly fed induction generator, DFIG)组为主，其定子直接挂接电网，转子通过三相交—直—交变换器实现交流励磁，可以通过定子、转子双通道实现电功率的交换。转子励磁变换器常采用背靠背三相两电平电压型PWM变换器，两PWM变换器按照其所在位置分别为网侧变换器(grid-side converter, GSC)和转子侧变换器(rotor-side converter, RSC)[4]。DFIG有超同步，亚同步，同步三种工作状态，本文研究的是GSC在整流工况实现功率因数控制，即亚同步状态。当DFIG处于亚同步时，需要GSC向DFIG供电，若电网发生不对称故障时，网侧将出现二倍频交流量，最终将会传递至转子侧，严重危害DFIG风电机组的机械系统安全，故在DFIG系统中，对GSC的控制尤为重要。

目前GSC的控制通常采用同步旋转坐标系下双环级联PI控制。在PI控制器下，GSC的控制虽然容易实现，但动态性能不是很理想，其中电流电压很难进行快速跟踪，因此想要达到理想的控制效果非常困难。

对于结构复杂，强耦合的非线性系统，经典控制理论很难对系统内部的变化做出描述，而基于微分几何的现代控制理论能够从系统的内部状态出发，充分描绘系统全部的动态过程。GSC本质也是一种变换器，从现代控制理论的角度，国内外也进行了研究，提出了一些相应的非线性控制理论。文献[5]提出电压外环使用滑模控制(sliding mode control，SMC)，但其SMC是基于稳态的滑模面，并不具备良好的动态性能；电流内环使用反馈线性化控制(feedback linearization, FL)，由于控制量的电流参考值在同步旋转坐标系下为常数，微分后为0，且引入了耦合项，最后化简的控制器的表达式和双环级联PI控制并无差异。文献[6]在不平衡电网下使用含有滑模补偿的反馈线性化控制，在dq坐标系中该控制的电流环将产生4个变量系数，再加上电压环的变量系数，调节难度极大。文献[7]使用FL直接电压控制，也是基于同步旋转坐标系，但因为存在直流母线电压的二阶微分，运算过程极为繁琐。

以上的控制方法相较于传统的PI控制方式，都改善了系统的动态性能，但是它们都有一个相同点：通过基于旋转同步坐标下反馈线性化控制律，这种控制方式不仅需要电网电压定向，还会出现与传统PI相同的控制结构[8 - 13]，甚至在不平衡电网下，增加控制的复杂性[14]。在总结前述文献成果的基础上，论文在理想电网下建立静止坐标系下的反馈线性化控制数学模型，这种方法避免了在同步旋转系下与传统PI控制相一致的情况，并且减少了因旋转因子带来的耦合项。通过增加含饱和函数的滑模控制，进一步提高动态性能，以实现网侧功率因数控制和电压稳定的目的。最后通过仿真验证上述控制方法的正确性。

1 静止坐标系下GSC数学模型

图1为GSC的结构框图。

图1 GSC结构框图Fig.1 Topology of grid side converter

图1中ua、ub、uc为变压器输出电压；ura、urb、urc为网侧变流器交流侧电压；R为寄生电阻，L为滤波电抗器的电感；ia、ib、ic为网侧变流器输入电流；C为直流母线滤波电容；udc为直流母线电压；iload为网侧流向转子变流器的电流。

三相静止abc坐标系下数学模型为：

(1)

根据GSC的拓扑结构，结合式(1)可得在两相静止αβ坐标系下的数学模型为：

(2)

(3)

2 GSC电流内环控制器设计

2.1 系统相对阶

对于y1=iα=x1=h1(x)，根据式(3)可得：

(4)

同理，对于y2=iβ=x2=h2(x)，可得：

(5)

(6)

由式(4)和(5)初步判断γ1=1，γ2=1(γ1为y1=h1(x)对应的子相对阶，γ2为y2=h2(x)对应的子相对阶)；通过式(6)可知为非奇异，则由此判定系统式(3)的相对阶γ=γ1+γ2=2，即γ=n(n为系统的阶数)。

2.2 FL控制律的确定

(7)

则：

(8)

即：

(9)

由式(9)可得FL控制律为：

(10)

式中v1、v2为新的控制输入。

通过FL控制律式(10)，可得输出与新的输入关系为：

(11)

为了实现跟踪控制，新的输入由下式确定。

(12)

式中：y1_ref=iα_ref；y2_ref=iβ_ref；e1=iα_ref-iα,e2=iβ_ref-iβ；iα_ref和iβ_ref均为参考电流。

其误差动态方程为：

(13)

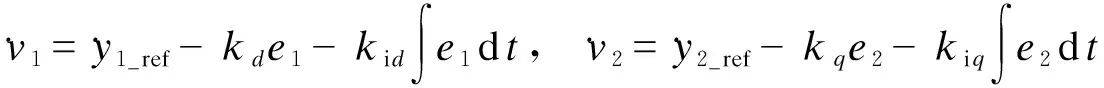
把式(12)代入式(10)可得：

(14)

又因为u1=uα-urα，u2=uβ-urβ，则GSC调制所需的合成期望电压为：

(15)

3 GSC电压外环控制器设计

选取滑模面函数[15 - 18]为：

S=udc_ref-udc

(16)

式中udc_ref为直流母线电压参考值。

通过选择合适的指数趋近律来限定滑模控制趋近阶段的运动轨迹以保证系统趋近运动的动态品质。由于系统在滑模面可能出现高频抖动，本文选用饱和函数sat(S)替换传统的sgn(S)来削弱其高频抖动，则指数趋近律如式(17)—(18)所示。

(17)

(18)

式中：k1、k2为滑模控制器参数，且k1>0，k2>0；ε为误差带，ε>0。

当系统稳定时，系统的直流母线电压udc将无静差跟踪参考值udc_ref，所以有：

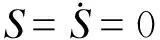
(19)

将式(19)代入到式(16)中，可得：

(20)

又由直流母线电压与功率关系，可得内环有功功率与直流母线电压关系为：

(21)

结合式(17),式(20)—(21)，可得网侧变换器直流母线电压外环的控制方程为：

p=(C[k1S+k2sat(S)]+iload)udc

(22)

综上，可得到GSC控制框图如图2所示。

图2 DFIG网侧、转子侧变换器联合控制原理图Fig.2 DFIG grid-side and rotor-side converter combined control schematic diagram

4 稳定性分析

定义Lyapunov函数为：

(23)

对式(23)求导，可得：

(24)

当|S|>ε时，有：

sat(S)=sgn(S)

(25)

将式(25)代入到式(24)，可得：

(26)

当|S|≤ε时，有：

(27)

将式(27)代入到式(24)，可得：

(28)

5 GSC参数设计

5.1 GSC网侧电感的设计

若忽略GSC网侧电阻R，稳态条件下，GSC网侧矢量关系如图3所示，且只考虑基波正弦电量。

图3 GSC网侧稳态矢量关系Fig.3 Steady-state vector of relationship GSC AC side

对图3中所示三角形，由余弦定理可知：

|V|2=|E|2+|Vr|2-2|E||Vr|sinφ

(29)

由GSC网侧电感的伏安关系式|Vr|=ωL|I|，代入式(29)，化简得

(30)

式中：E为网侧变压器电动势矢量；V为GSC网侧相电压矢量；Vr为GSC网侧电感电压矢量；I为GSC网侧相电流矢量。

因为：

|V|max=ηudc

(31)

式中：η为PWM相电压最大利用率。

即：

|V|≤ηudc

(32)

将式(32)代入式(30)，得GSC网侧电感为：

(33)

由式(33)可得：

(34)

GSC采用SVPWM控制，且忽略GSC损耗，则有：

(35)

式中：p为GSC交流侧有功功率；q为GSC交流侧无功功率。

满足单位功率因数下，将式(35)代入式(33)可得：

(36)

然而根据实际情况网侧电感都带有寄生电阻，考虑网侧电阻时的GSC网侧矢量关系如图4所示。其中虚线矢量是忽略电阻影响时的GSC网侧电压矢量V′，实线矢量则是考虑电阻影响时的GSC网侧电压矢量V。

图4 GSC网侧电阻对其网侧电压矢量的影响Fig.4 The influence of GSC AC grid side resistance on AC side voltage vector

如图4所示，GSC工作在单位功率因数下，由于|V′|>|V|，因此当考虑GSC网侧电阻影响时，GSC交流侧基波电压幅值有所减小，在相同条件下运行时，GSC网侧电感上限值应相应增大。

5.2 GSC直流侧电容的设计

当GSC直流电压给定为直流电压参考值时，电压调节器采用滑模控制器，则在GSC实际直流电压未超过参考值之前，滑模控制器的输出将会向滑模面趋近。由于滑模控制器输出为GSC网侧功率参考值，在给定直流电压下，此时GSC直流侧将以最大电流Idm对直流电容及负载充电，从而使GSC直流电压以最快速度上升。这动态过程等效电路如图5所示。

图5 GSC直流电压跃变时等效恒压源电路Fig.5 Equivalent constant voltage source circuit when GSC DC voltage jumps

由图5易知：

(37)

式中：RLe为转子侧等效负荷电阻；Idm为最大电流；τ1为时间常数。

化简得：

(38)

(39)

6 关于转子侧PWM变换器及其影响

由于直流环节的解耦作用，DFIG系统中的各变换器功能相互独立，其中GSC主要控制直流侧稳定以及获得良好的交流输入性能，并不会直接参与对DFIG进行控制；RSC则是用以实现DFIG及其整个双馈风力发电系统的运行控制，其控制的有效性将直接影响DFIG风电系统的运行性能。

在保证GSC控制直流侧稳定情况下，为了保证最大风能跟踪，根据其原理，在不计机械损耗的条件下，DFIG输出总电磁功率参考值由文献[19]可知：

(40)

式中：Popt为最佳功率；ωm为发电机转速；ωr为风力机转速；np为DFIG极对数；N为齿轮箱增速比；Pe_ref为总电磁功率参考值；Kw是与风力机有关的常数。

根据总电磁功率与定子有功之间关系，可以得到定子输出有功参考值Ps_ref，即：

(41)

式中：Pcus为定子铜耗；s为DFIG运行转差率。

通过式(41)并对定子输出有功进行闭环控制，进而实现对总电磁功率的有效控制，控制原理图如图2所示。

7 仿真分析

为了验证本文所述控制策略的有效性，在MATLAB/Simulink环境中对其所述控制策略进行仿真。GSC仿真的主要参数按照上文参数要求，设计如下：变压器输出线电压190 V/50 Hz；交流侧滤波电感10 mH；电阻5 Ω；直流侧初始电压为0，参考电压220 V；直流侧电容470 μF；负载为RSC；ipm开关频率为10 kHz。图6为仿真结果。

图6(a)和图6(b)为静止坐标系下网侧参考电流和实际电流，实际电流能够较好地跟踪参考电流；图6(c)上半图为传统双环级联PI控制下的iα、iβ波形，下半图为外环为滑模控制，内环为FL控制下的iα、iβ波形，对比可知，传统控制方式下的iα、iβ具有很明显的超调，而在非线性复合控制方式下的动态过程过渡非常平滑；图6(d)上半图为外环使用PI控制内环为FL控制下的iα、iβ波形，下半图为外环使用滑模控制器，内环使用FL控制下的iα、iβ波形，如图6(d)所示，在0.01 s使用非线性复合控制的6(d)超调更小，动态性能更好。图6(e)为非线性复合控制下的三相输入电压和网侧电流波形，图中三相输入电压和网侧电流同相位，实现了单位功率因数控制。图6(f)和图6(g)分别为传统控制下的直流母线电压udc和非线性复合控制下的直流母线电压udc，通过两图对比可知，传统控制下的udc在0.05 s前具有很大的超调，在0.13 s才趋于稳定，而非线性复合控制下的udc并没有超调，且在0.025 s就达到稳态，具有很好的快速性。

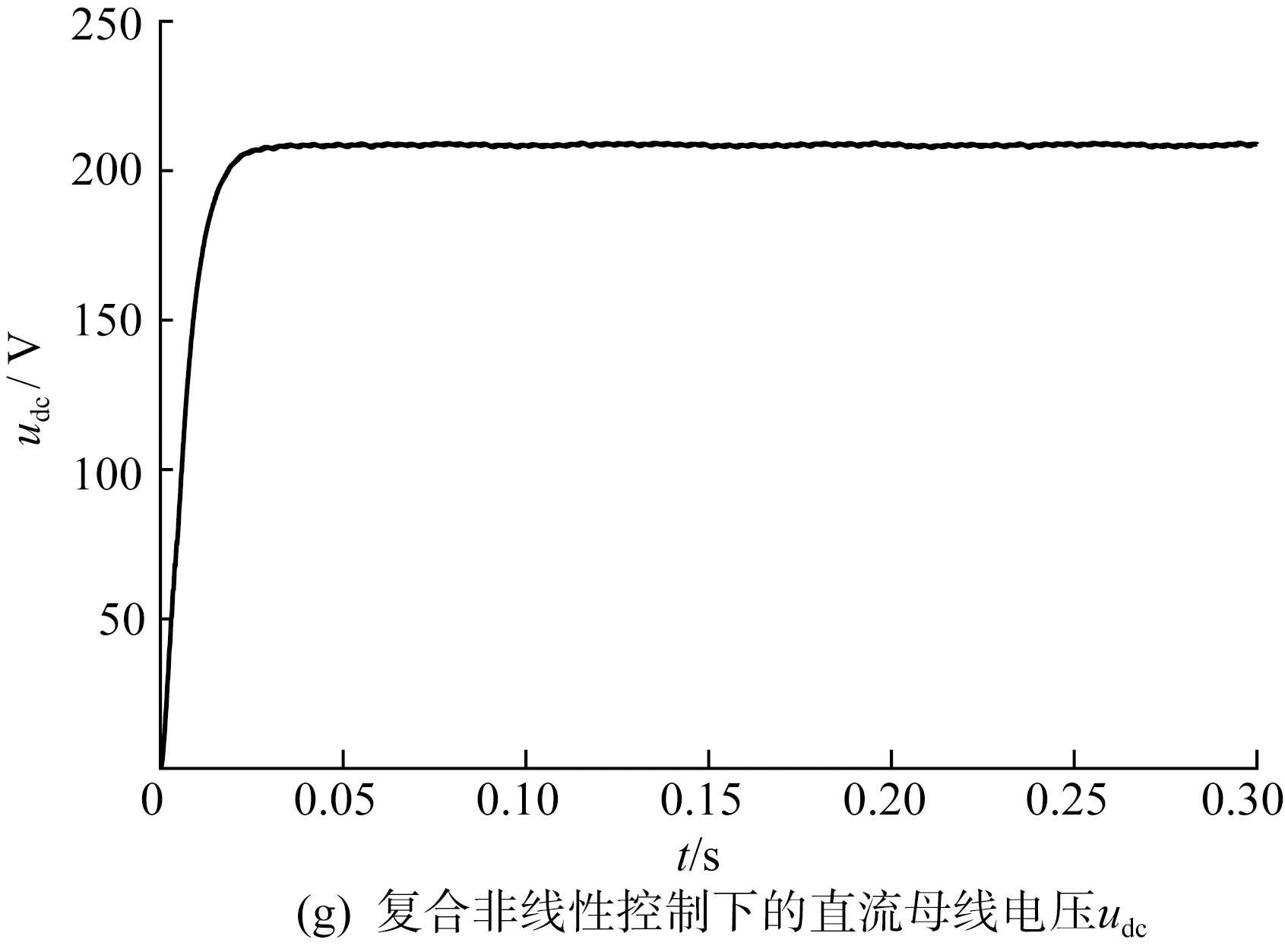
图6 仿真结果Fig.6 Simulation results

通过对GSC的数学模型搭建以及仿真结果的验证，证明了本文所提的控制策略在平衡电网下GSC控制具有优秀的动态性能。

8 结语

本文以DFIG网侧变换器作为研究对象，提出了利用反馈线性化理论在两相静止坐标下对电流进行控制的方法，相比在同步坐标系下的控制方式，本控制策略无需电网电压定向，减少了耦合项的引入，避免出现与传统PI相同的复杂结构，实现了反馈线性化快速解耦；同时电压外环采用含饱和函数的电压滑模控制，提高了系统的动态性能。仿真结果表明，该控制方法具有很好的动态性能，并且实现了直流母线电压的稳定以及网侧功率因数控制，验证了理论的正确性。上述控制策略也为不平衡电网下DFIG的GSC非线性控制提供了理论基础。