基于开关函数的LCC-HVDC输电系统谐波计算方法

洪潮，代锋，曾德辉，吴争荣，吴为，王钢

(1. 南方电网科学研究院，广州510663；2. 华南理工大学电力学院，广州510640；3. 广州嘉缘电力科技有限公司，广州510640)

0 引言

对于传统直流输电系统(line-commutated converter high voltage direct current, LCC-HVDC)，由于存在基于晶闸管的换流器等非线性设备，造成换流器交直流侧均含有谐波，这将危害电力设备运行安全，降低电网运行的经济效益[1 - 4]。目前，对于谐波的计算和分析主要集中在低次谐波以及仿真分析方面。而随着电网规模的扩大和电力电子设备的增加，高次谐波成为需要分析的新问题，近几年发生的几起高次谐波振荡问题也给电网安全造成了极大的危害[5 - 6]。因此，有必要对高次谐波，特别是作为主要谐波源的换流器产生的谐波进行计算和分析。

国内外对换流器产生的谐波开展了大量的研究，提出的模型主要包括电磁暂态模型以及动态相量模型等[7 - 11]。电磁暂态仿真方法是基于电磁暂态仿真软件(如PSCAD/EMTDC、EMTP等)建立含有换流器的直流系统详细模型，求解相应的时域解，但其求解耗时较长，也不能揭示谐波产生及交直流侧谐波相互作用的机理；而基于开关函数的动态相量模型很好地平衡了速度和精度的关系，能够揭示换流器换流及谐波产生机理，逐渐成为重要的换流器谐波研究方法。

目前文献对谐波的分析多侧重于低次谐波的分析，较少考虑高次谐波的计算和分析[12 - 14]，而低次谐波数值一般相对较大，不同精度的模型造成的误差相对不大，因此，存在较少考虑开关函数精确求解的问题。如文献[15 - 17]中，对开关函数的计算存在忽略换相过程、将换相曲线等效为直线、仅考虑开关函数傅里叶级数的基波分量等问题，这与实际情况并不相符，也不利于高次谐波的计算，并且其采用两端直流输电系统建立对应的直流电压和电流方程，不仅增加了计算量，也由于需要更多的已知参数而不具有求解灵活性。

因此，为了解决各次谐波，包括高次谐波的求解问题，提高计算精度，同时使计算模型更加接近真实工程，并揭示谐波产生机理，本文考虑了符合实际情况的开关函数，通过提出基于开关函数的谐波计算方法对LCC-HVDC中换流器产生的各次特征谐波进行准确计算，从而揭示谐波的产生机理，为高、低各次谐波相关分析及抑制提供参考。

1 谐波计算模型

1.1 谐波模型建立

首先，本文通过图1所示的三相六脉动换流器的结构示意图，引出六脉动换流器的谐波模型建立方法。

图1 三相六脉动换流器的结构Fig.1 Structure of a three phase six pulse converter

根据调制理论可知：直流电压可以视为换流器对交流电压的调制，交流电流可以视为换流器对直流电流的调制，即：

(1)

式中：ud、id分别为直流电压和直流电流；ua、ub、uc分别为三相交流电压；ia、ib、ic分别为三相交流电流；Sua、Sub、Suc分别为a、b、c三相对应的电压开关函数；Sia、Sib、Sic分别为a、b、c三相对应的电流开关函数。

将式(1)进行傅里叶变换，可得：

(2)

式中k、m均为谐波次数，且k≠m。

对于12脉动换流器，一般将两组6脉动换流器进行串联，而且所连变压器分别采用Yn/△和Yn/Y接线。为了减少计算量，同时考虑到正常情况下，非特征谐波足够小，可以忽略不计[18]，因此，可得12脉动换流器谐波模型，如式(3)所示。

(3)

式中：上标y、d分别表示12脉动换流器的Y桥臂和△桥臂相应相量，j=a,b,c。

1.2 开关函数求取

开关函数可以反映换流器的工作过程。电压、电流的开关函数标准波形如图2所示。

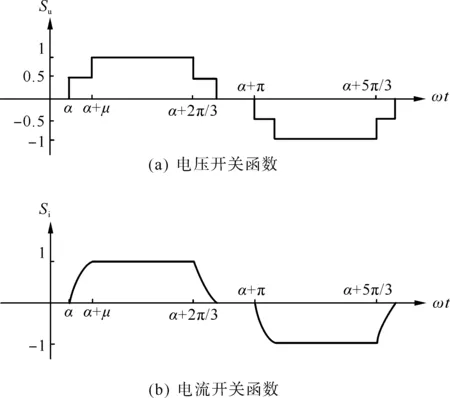
图2 开关函数波形Fig.2 Switching function waveforms

从图中可以看出，对于电压开关函数，换流阀导通期间，Su=±1；换相期间，Su=±0.5；关断期间，Su=0；而对于电流开关函数，由于电流值不能突变，其换相期间的值为逐渐变化的曲线。

假设图1中，首先只有换流阀5和6导通，在ωt=α时，阀5开始向换流阀1换流，此时有：

(4)

式中：E为换相电压幅值；Lr为交流系统等值换相电感；i1、i5分别为换流阀1和5上流通的电流。

由于换流阀1和5中的电流之和等于直流电流，因此，对式(4)进行积分运算，可得：

(5)

式中：Xr为交流系统等值换相电抗；α为触发角。

最终，当换流阀5和6完全换相为换流阀6和1后，换流阀5将关断，i1和i5将分别等于Id和0。

因此，通过以上分析，可得换相过程中电流开关函数为：

(6)

式(6)采用了曲线形式对换相期间的开关函数进行描述，相对于目前相关文献[15 - 17]中忽略换相过程、将换相曲线等效为直线、仅考虑开关函数傅里叶级数的基波分量等处理方法更符合实际，也具有更高的计算精度。

2 直流系统等值电路及模型求解

2.1 直流控制特性

图3为CIGRE Benchmark标准测试系统的Ud-Id特性曲线[19]，Ud和Id为直流电压和电流。图中的细实线A-I是整流器运行于最小触发角αmin控制时逆变侧控制器的稳态运行特性曲线，粗实线A-Z是逆变器运行于定关断角γ0控制时整流侧控制器的稳态运行特性曲线。

图3 直流输电系统的Ud-Id特性曲线Fig.3 Ud-Id characteristic curve of an HVDC system

因此，基于图3所示特性曲线，可得考虑直流控制策略情况下的整流侧和逆变侧控制器稳态运行特性对应的直流电压和电流关系分别为：

(7)

(8)

式中a1、b1、a2、b2均为分段函数参数。

需要强调的是，图3的特性和式(7)、(8)可用于故障情况下的暂态谐波分析，而如果只关注直流输电正常稳态运行下的工况(即运行于点A的工况)，则应不予考虑。

2.2 直流等值电路

直流输电系统在正常情况下的等效电路如图4所示。

图4 直流系统谐波阻抗等值电路Fig.4 Harmonic impedance equivalent circuit of HVDC

基于电路理论，由图4得直流等值谐波阻抗为：

(9)

式中：Zl(m)为直流线路m次等值谐波阻抗；Zf(m)为直流滤波器m次等值谐波阻抗；Zs(m)为平波电抗器m次等值谐波阻抗；Ze(m)为对侧换流器的直流侧m次等值谐波阻抗，可由式(10)求得[20]。

(10)

式中：Zc(m)为换流器的m次换相阻抗；Zd(m)为从本侧换流器直流侧看进去的m次等值谐波阻抗。

因此，换流器直流侧m次谐波电流为：

id(m)=ud(m)/Zd(m)

(11)

最终，通过式(3)得到了基于开关函数的换流器交直流谐波相互作用关系，通过式(11)得到了直流系统的电压、电流关系，然后通过对交流侧潮流的分析得到了式(12)所示的关于交流电压、电流的关系。

uj=f(ij)

(12)

式中：uj为j相交流电压；ij为j相交流电流；f为交流电压和电流之间的关系函数；j=a,b,c。

最终联立式(3)、(9)—(12)即可求解得到直流系统各次谐波。并且，通过开关函数反映了换流器导通过程，通过调制理论反映了交直流侧电压、电流之间的关系，在它们的共同作用下，最终产生了复杂的谐波关系。

2.3 模型求解

为了对本文建立的谐波计算模型进行求解，提出的求解策略如图5所示。

图5 谐波模型计算流程图Fig.5 Calculation flowchart of harmonic model

总体的求解思路为：基于换流器工作原理及相关参数，计算电压和电流开关函数，然后将谐波的求解过程分为交流系统、直流系统以及交直流交互系统(换流器系统)3个组成部分：根据本文第2节建立关于直流电压、电流直流分量和谐波分量的关系；根据交流潮流计算方法形成式(12)所示的交流电压、电流的关系；根据第1.1节中基于开关函数的谐波计算方法建立关于交直流谐波电压、电流的相互作用关系方程。最终通过联立各关系式即可求解得到交流侧和直流侧的谐波电压、电流值。

3 谐波计算方法验证

3.1 特征谐波分析

为了对本文所提出的换流器谐波计算方法进行可行性及准确性验证，利用PSCAD软件中的CIGRE Benchmark模型开展了仿真，其中在模型中设置短路比SCR为2.5，交流系统的短路容量为2 500 MVA，交流系统阻抗特性如图6所示，将仿真结果与本文的基于开关函数的模型计算结果进行对比。

图7给出了各次特征谐波的计算值与仿真值的对比结果。

图6 交流系统阻抗特性Fig.6 Impedance characteristics of AC system

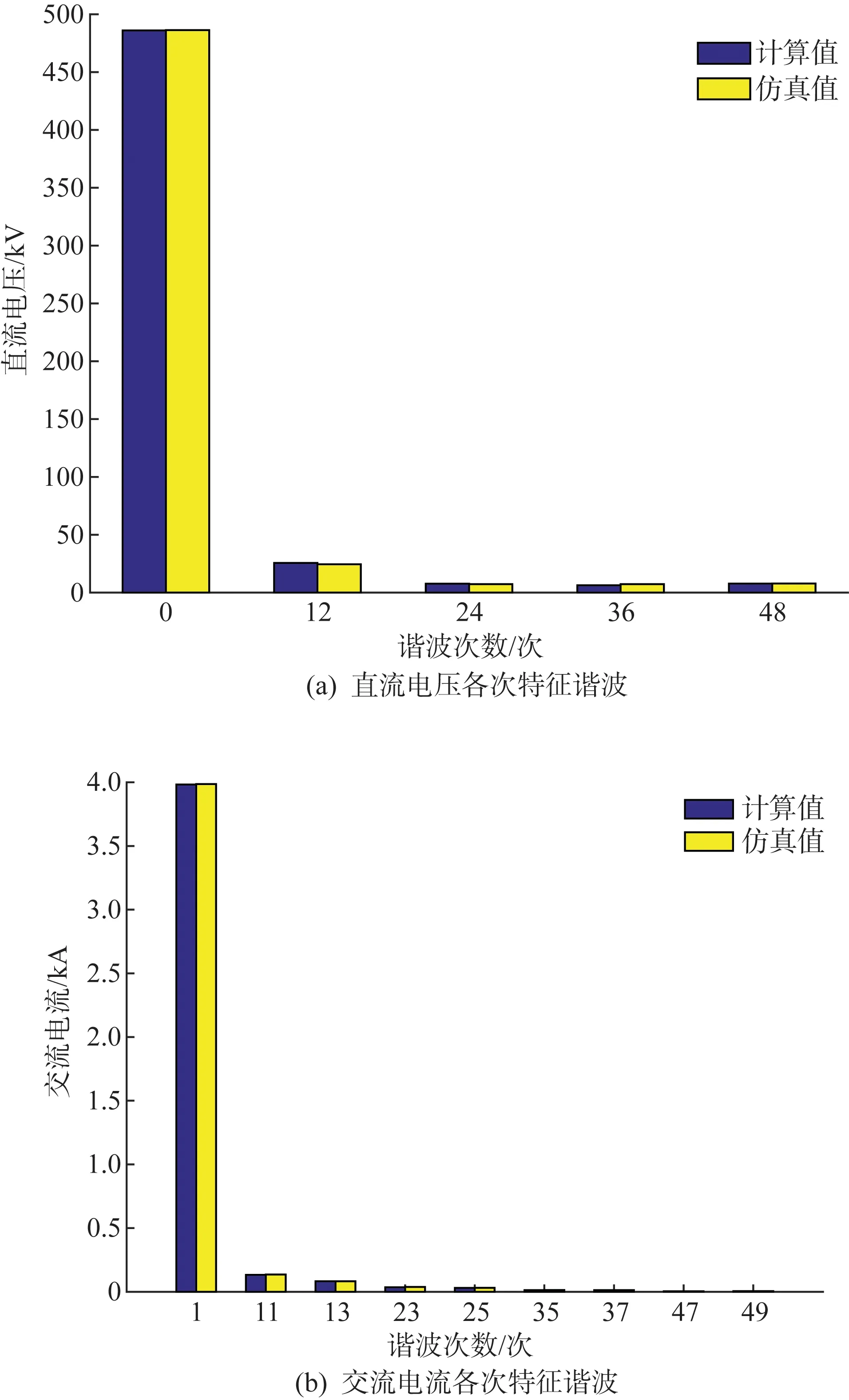
图7 各次特征谐波的计算和仿真对比结果Fig.7 Comparison of calculation results and simulation results in each characteristic harmonic

从图7可以看出：本文方法计算的直流电压直流分量以及12、24、36、48次直流电压特征谐波分量、基波电流分量以及11、13、23、25、35、37、47、49次交流电流特征谐波分量均与仿真结果一致，具有较高的精度，能够满足谐波计算的要求。另外，由于交直流谐波之间的交互作用，谐波在48/49次后依然存在一定的数值，从本文的分析可知，其相互作用会一直作用至更高次谐波。

进一步通过交流谐波电压和电流计算谐波阻抗，可得换流器交流侧阻抗幅频特性如图8所示。为了验证所提算法的优越性，与文献[21]中的谐波计算数据进行了对比，结果如图9所示。由图9可见，本文的方法精度较高。

图8 换流器交流侧等值阻抗的幅频特性曲线Fig.8 The amplitude-frequency characteristic curves of equivalent impedance at AC side of converter

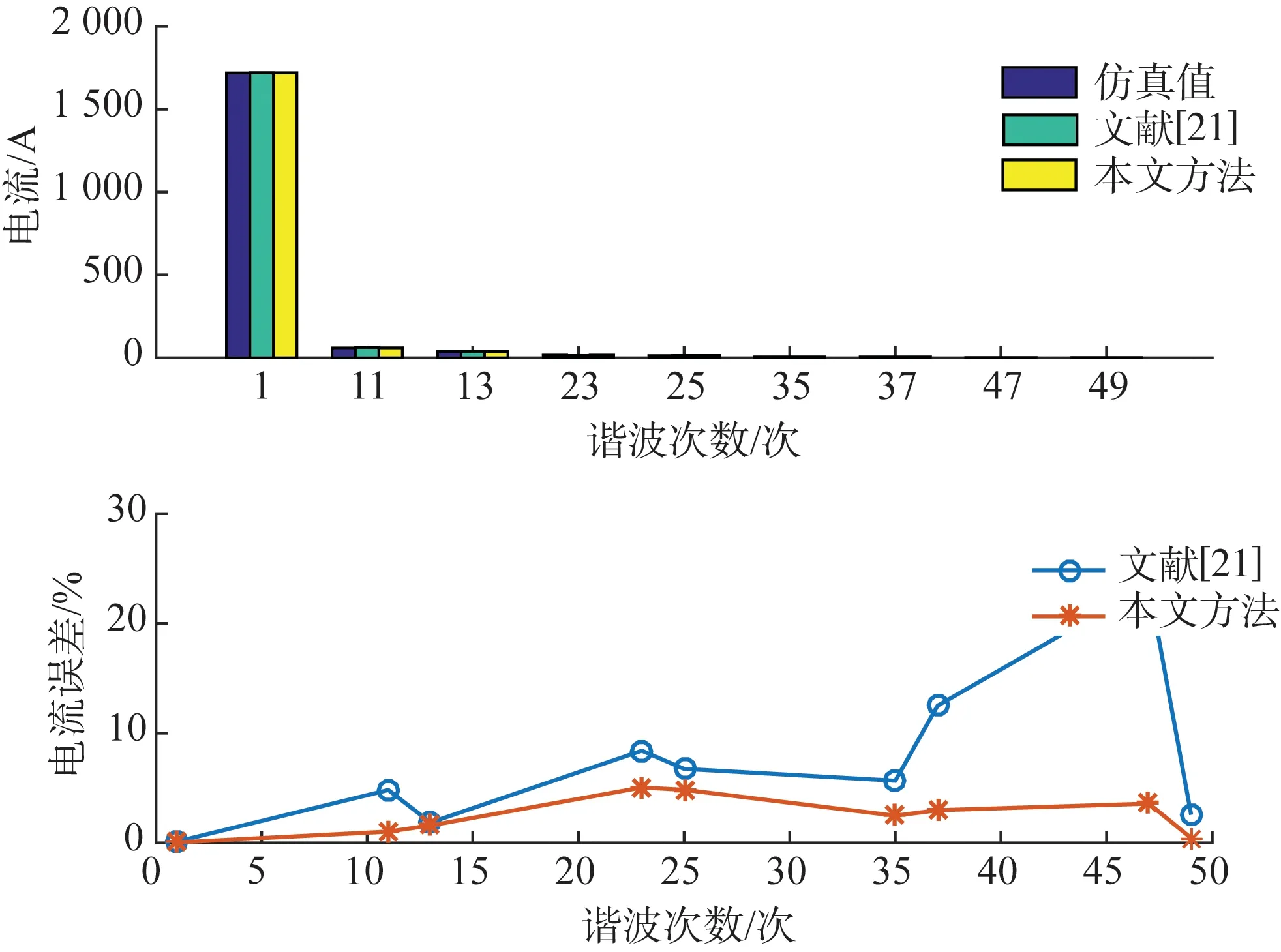
图9 本文方法与文献[21]的对比结果Fig.9 Comparison between the proposed method and the reference [21]

3.2 误差分析

本文所提基于开关函数的谐波计算方法虽然精度较高，但仍然存在误差，这是由于开关函数计算过程中并不能完全吻合实际。表1给出了本文模型部分数据点的电流开关函数值。其中，数据编号表示从起始时刻开始的开关函数采样/计算离散点编号值，编号1- 3处于换流阀关断区间，编号66- 69处于换相区间，编号117-119处于导通区间。

由表1可见：在换流阀关断情况下，由于仿真中关断电阻非无穷大，仍然存在一定的换流阀电流，所以存在一定的开关函数值，而开关函数的计算值更加理想化，因此仿真和计算值存在一定误差。但此时电流开关函数值均很小，由式(3)可见，该误差并不会显著影响最终的计算结果。在换流阀换相期间，由于本文采用了曲线对换相期间的开关函数进行描述，因此计算误差较小。另外，在换流阀导通期间，由于开关函数值相对更大，因此仿真和计算值误差最小。通过以上分析可发现，在开关函数误差以及计算误差等的综合影响下，虽然导致仿真值和计算值存在一定的误差，但相对于目前文献中忽略换相过程、将换相曲线等效为直线、仅考虑开关函数傅里叶级数的基波分量等处理方法仍然具有较高的精度优势。

综上，通过对直流电压、交流电流的各次谐波以及开关函数的计算，验证了本文方法能够用于高次谐波计算，解决了目前较少进行高次谐波计算的问题，且具有较高的精度。

4 结论

针对目前谐波研究较少进行高次谐波计算和分析，且由于开关函数的计算公式不同导致计算也存在不同的误差的情况，本文为了计算直流系统各次谐波，特别是高次谐波，提高计算精度，通过基于开关函数的调制理论对换流器进行了建模，使计算模型更接近真实工程，同时，通过直流侧等值谐波阻抗来反映直流电压、电流关系的方式以及整体交直流方程联立求解的方式，既直观反映了相关谐波的相互作用关系，也提高了谐波求解灵活性，实现了对交直流侧的特征谐波，包括高次谐波的准确计算，从而可分析谐波的产生机理。

从计算和分析结果可以看出：本文提出的方法具有较高的精度，能够满足对各次特征谐波的计算；由于谐波相互作用，将产生至很高次的交直流侧电压、电流谐波，并且随着谐波次数的增加其幅值呈现减小的趋势；换流器本身的换流原理决定了其会产生一定的谐波，进而在交直流侧谐波的交互作用下形成复杂的谐波关系。本文的计算方法和结果可以为直流输电系统的谐波计算和抑制提供方法基础和理论参考。