基于组合赋权-TOPSIS交直流配电网能效评估

曹华珍，王天霖，张黎明，高崇，张真，杨墨缘，欧阳森

(1. 广东电网有限责任公司电网规划研究中心，广州510080；2. 华南理工大学电力学院，广州510640)

0 引言

21世纪以来，经济的高速发展伴随的能源需求的急剧攀升，能源的供需问题日益突出。目前我国能源效率仅为33%，远低于发达国家，传统配电网更易出现电能损耗大，10 kV配电网损耗占据整体电网损耗的一半[1]。如何提高能源利用率[2]，降低配电网损耗是当前亟待解决的问题。在此之前对配电网进行科学、合理的能效评估显得尤为重要，既有理论研究的必要性，也有工程应用的需求。

国内外在能效评估领域已有部分研究成果，部分学者从优质电力园区中多种能源之间转化的效率考虑能源利用率，对包含冷/热/电等多能源的综合能源系统进行能效评估[3 - 4]。现有传统配电网的能效评估多从网架结构、设备的规划与运行参数、技术经济等电网侧方面对能效进行评估[5 - 9]。针对传统交流配电网存在线损高、电能质量不稳定等问题[10]。现解决方案是引入直流供电技术，可改善电能质量，降低DG并网时的换流损耗，同时需进一步考虑新能源出力和负荷的不确定性，对新能源消纳的能力进行评估[11]。而直流环节的接入有赖于电力电子设备，随着电力电子变压器(power electronics transformer, PET)的快速发展，其应用于直流环节的变流连接具有较好的效果[12]；同时配电网在发、变、配、用等环节的能效影响因子发生了改变。因此，基于源网荷3方面并考虑DG和PET等电力电子设备接入对能效评估的影响的研究具有重要意义。

交直流配电网电源侧分布式电源(distributed generation, DG)的类型、波动性、分布位置以及渗透率等[13]均会影响电网损耗，同时直流环节的引入提高了DG渗透率，将对能效产生新的影响。文献[14]计及电源侧各类DG出力波动特性，电网损耗会随概率潮流分布而发生显著改变；文献[15]以网损费用最低为约束目标，讨论了DG接入的位置和容量对系统的影响。文献[16]讨论了分布式储能系统的效率和能量管理，其充放电效率会对能效的影响。文献[17]考虑了能源系统的多能流特性与DG对设备利用率的影响。

交直流配电网的电网侧除了传统线路、配电变压器等因素外，DG的并网将引入变流器，而直流配电网的变流连接引入PET，其具有诸多优势是未来发展的趋势，大量电力电子设备接入必然对能效产生新的影响。文献[6]考虑了电网侧新型设备PET的接入，并从设备静、动态参数以及损耗指标3方面对交直流配电网的能效进行评估；文献[7]建立了技术经济评价指标，讨论配电网供电可靠性、电压合格率、综合线损率等综合性能的影响。

交直流配电网负荷侧的用电波动性、逆变器等用户设备效率以及节能管理方式等均对能效产生影响。文献[18]建立电力用户负荷侧能效评估模型，讨论了耗能设备效率、节电率等关键指标的影响；文献[19]考虑了源网荷协调控制对电网降损效果的影响，但未分析设备规划指标和源荷波动率。

关于评估方法的研究，文献[20]针对综合能源系统能效评估提出AHP法，存在一致性检验问题。文献[21]提出基于灰色AHP的变电站能效综合评估模型，忽略了原始数据所包含的信息造成权重过于主观化。文献[22]提出G1-反熵权法用于分布式能源系统的多指标评价，并取得良好的效果。因此本文考虑在此基础上结合逼近理想解排序法(technique for order preference by similarity to ideal solution, TOPSIS)，提出一种组合赋权-TOPSIS法对交直流配电网能效进行评估。

现有指标体系尚不够全面，缺乏对源荷波动率、节电率等影响较大因素的考虑，且现有文献仅从电网角度出发提取指标，少有文献考虑从配电网的发、变、配、用等环节对指标进行细化并整理归纳成为能效评价指标体系。本文从源网荷3方面构建了一套适用于交直流配电网的能效评价指标体系，该指标体系考虑的因素全面而简化；并拟建立基于G1-反熵权法确定指标的主客观权重，采用TOPSIS法评估充分反映各方案之间的差距和实际情况。最后通过模拟算例验证了指标的合理性和模型的可行性，为能效评估提供一定的参考价值。

1 能效影响因素机理分析

1.1 典型交直流配电网拓扑

现有中低压配电网大部分通过变压器和变流器增加直流环节，再通过变流器进行负荷供电，而新引入的PET可灵活接入DG并可直接进行直流供电，因此计及PET增量和传统变流方式存量并考虑到DG接直流母线可降低换流损耗，本文以图1典型的交直流配电网拓扑结构为例，主要包括：配电变压器、DG、交直流负荷和线缆以及各种电力电子设备等。本文将配电网中分布式电源划分为电源侧，将公共连接点(point of common coupling，PCC)以后的线路划分为负荷侧，其余归纳到电网侧，从源网荷3个方面考虑对电力系统能效水平的影响。

图1 交直流配电网拓扑示意图Fig.1 AC/DC distribution system topology diagram

1.2 电网侧能效机理分析

图2 线路Π型等值电路Fig.2 Equivalent circuit of line π-type

电网侧线路等值电路如图2所示，线路损耗ΔPL包括两部分：电导损耗PG和负载损耗PR，PG在配电网中一般较小做忽略处理，线损理论计算公式如式(1)所示：

(1)

式中：ΔEL为月总电量损耗；EL为月总传输电量；T为月总小时数；R为台区等值电阻；Irms为均方根电流；Kf=Iif/Iav为负荷形状系数；Iif为日均方根电流；Iav为日平均电流；ρ为线路电阻率；l为线路供电半径或总长度；K为三相不平衡系数；UN为运行电压；λN为功率因数；A为线路截面。通过对月电量损耗率分析，线路提高运行电压、功率因数以及增大线路截面积可以提高电网能效。结合式(1)，当存在谐波、三相不平衡等电能质量问题时附加损耗如式(2)—(3)。

(2)

(3)

式中：ΔPh为谐波附加损耗；Iin(i=a,b,c)为三相第n次谐波电流有效值；Rn为第n次线路的谐波电阻；式(3)中：ΔPunbalance为三相不平衡产生的附加损耗；Ii(i=A,B,C)为三相电流值；Iav为三相电流平均值；R为单相等值电阻值，同理谐波和三相不平衡对变压器损耗也有影响，不再累述，综上可见电能质量越差，能效水平越低。

由于PET在DG的灵活接入、降低谐波以及提高能源利用率等方面具有优势，PET接入容量的增加，将降低传统变流过程中的损耗提升能效水平，配电网的直流侧与交流侧变流连接采用PET将成为未来发展的趋势；同时电网侧大量VSC的使用，其工作效率会影响能效；交直流配电网中直流配电和交流配电损耗可由式(4)比较。

(4)

式中：ΔPDC为直流系统功率损耗；ΔPAC交流系统功率损耗；cosφ为交流系统功率因数；k为直流电压与交流电压幅值比；UAC、UDC分别为交流线电压和直流单极对地电压；rAC、rDC分别为交直系统等效电阻；在配送功率相同的情况下，直流配电网的线路功率损耗只有交流配电网线路功率损耗的19.55%[23]，直流供电容量的增加可提升电网能效。为提高指标的全面性，结合已有文献补充一些电网侧已有的规划和运行参数，电网侧的影响因子与能效关系如表1所示。

表1 电网侧的影响因子与能效关系表Tab.1 Relationship between grid side energy efficiency and impact factors

1.3 电源侧和负荷侧能效机理分析

为量化分析DG接入前后对系统损耗的影响，DG接入配电网后简化等值电路如图3所示，等负荷需求下电网损耗相对变化量如式(5)所示。

图3 DG接入后配电网等值电路图Fig.3 equivalent circuit diagram of distribution network after DG access

ΔP=IL(RL+RD)-IDGRDG-I′LRL-IDRD=

(5)

式中：ΔP为DG接入前后网损的变化量；IL、I′L分别为DG接入前后电网支路电流；IDG、ID为DG和负荷支路的电流；SDG、UN为DG接入容量和额定电压；RL、RDG、RD为对应支路的等效电阻，结合式(5)接入容量的增加可提高系统能效。

直流环节提高了DG渗透率，高渗透率下DG的随机性与间歇性增大了源荷波动，引起电网电压不均一波动，电压分布不均衡度量化公式[24]如式(6)所示。

ε=D(V)=E(V2)-E(V)2

(6)

式中：D(V)为全网节点电压方差；E(V)为节点电压均值，即期望值。电压分布不均衡度与网络损耗都和网络各节点电压差值的平方项相关，所以电压波动和网络损耗具有较高的相关性。为降低其电网的影响，需装设储能装置(energy storage, ES)用以削峰填谷，其充放电效率正向反应能源利用率。负荷侧存在城市道路的过度照明、高损耗设备运行等问题，根据文献[25]和低碳环保理念的要求，倡导淘汰高损耗的设备，提高节电率成为提升能效的发展趋势。电源侧、负荷侧的影响因子与能效关系如表2所示。

表2 电源侧、负荷侧的影响因子与能效关系表Tab.2 Relationship between energy efficiency and influencing factors on power supply side and load side

表3 基于源网荷的交直流配电网能效综合评价指标体系 Tab.3 Comprehensive evaluation index system of energy efficiency of AC and DC distribution network based on source load

2 交直流配电网能效指标体系构建

本文考虑从配电网的发、变、配、用等环节对指标进行细化并整理归纳成为能效评价指标体系。结合上文对能效影响因子的分析，源网荷3方面相关指标计算公式如下，指标编号如表3所示。

2.1 电源侧指标分析

1)DG容量占比。相同工况下分布式电源并网可减少交流侧输送容量，降低输电损耗。

(7)

式中：PDG为分布式电源发电容量，其包含储能的总容量；PL为系统负荷需求总容量。

2)DG出力波动率。DG出力波动性越大，并网所引起的不确定性及并网损耗越大。

(8)

3)ES充放电效率。与其自身性能、运行状况、维护情况有关，是评估资源利用率和损耗的综合指标。

(9)

式中：Edis为放电量；Echa为充电量。

2.2 电网侧指标分析

1)导线截面积及供电半径。表征线路规划参数。

(10)

(11)

式中：S、l分别为单条线路导线截面积和供电半径；NL为馈线条数。

2)直流供电容量占比。等功率配送,直流配电网的功率损耗低于交流配电网功率损耗。表征直流潮流对能效的影响。

(12)

式中：PDC直流供电总容量；PL负荷总容量。

3)高损配变容量占比。表征配变的损耗。

(13)

式中：Sloss_i为第i台高损配变的容量；ST为所有变压器容量。

4)PET容量占比。含有PET的交直配电网能效水平较高[6]。表征电力电子设备引入的影响。

(14)

式中：SPET_i为第i台PET的容量；ST为所有变压器容量。

5)均方根电流。上述分析线损与负荷电流成正比。表征用户需求对能效的影响。

(15)

式中：k为电流形状系数；WP、WQ分别为有功电能与无功电能读数；t为统计时间。

6)变压器负载率。变压器运行在合理的负载区间内可实现经济运行。表征电网运行方式的影响。

(16)

式中：ST_ave变压器平均输出功率；STN变压器额定容量。

7)线路负载率。线路负载率随峰谷差的增大而下降，峰谷负荷差距越大，则负载率越低，电网运行所产生损耗越大。表征电网运行方式的影响。

(17)

式中：SL_max为线路最大负荷；Sline_max为线路最大容载量。

8)总谐波畸变率。谐波电流会在设备运行时产生附加谐波损耗。表征电能质量的影响。

(18)

式中：I(1)为电压基波分量有效值；I(h)为电压的第h次谐波分量有效值。

9)三相不平衡度。三相电流不平衡会使得线路及变压器损耗增加[5]，基于负序的电压不平衡度计算方法。表征电能质量的影响。

(19)

式中：U1三相电压的正序分量方均根值；U2为三相电压的负序分量方均根值。

10)功率因数。功率因数低不仅影响生产产品的质量，还会降低配电网能效水平。表征电能质量的影响。

(20)

式中P、Q分别为馈线的有功与无功功率。

11)VSC效率。表征电力电子设备接入的影响。

(21)

式中Pvsc_i、Pvsc_o分别为变流器输入输出功率。

2.3 负荷侧指标分析

负荷总波动率。负荷波动会引起电压波动，并改变电网的潮流分布特征，增大线损。统计时间周期T内，用户总负荷曲线平均波动率为

(22)

高损设备容量占比。电力用户侧存在低效用户配变及用电设备等高损设备严重影响电网能效。

(23)

式中：∑SLoss为高损设备总容量；∑SL为电力负荷侧用电总容量。

节电率。提出节电率的目的是为了提升城市照明和用户用电的节能意识。

(24)

式中：WS为根据负荷预测的预计用电量；WR为节电条件下实际用电量。

逆变器效率。用户侧逆变器的大量使用影响负荷侧能效。

(25)

式中：NS为用户逆变器类别数；nS为各类逆变器台数；pi第i类逆变器容量占比；ηij为第i类第j台逆变器转换效率；N为总逆变器台数。

2.4 交直流配电网能效指标体系

整理筛选上文所提能效影响因子并参考相关国标[23 - 28]，本文构建了3个指标层级共计19项指标综合评价指标体系如表3所示，第1层S={交直流配电网能效水平}，第2层{S1,S2,S3}={电源侧能效指标,电网侧能效指标，负荷侧能效指标}以及第三层指标P层。本文从交直流配电网发、变、配、用4个环节即源网荷3个角度全面系统对能效进行评估。指标能够覆盖整个交直流配电网系统，既具代表性，又可体现差异化。其中指标与能效呈现正相关，则为正向指标，反之为逆向指标,若最优值为中间值则为区间指标。

3 综合评估模型步骤设计

本文指标体系中电源侧和负荷侧的指标数目远不及电网侧，采用G1-反熵权法可赋予较少指标数的电源侧与负荷侧的指标较高权重，突出能效评估中电源侧和负荷侧指标的重要性，因此该方法非常适合本文的需求，传统组合赋权均采用线性组合方式，而线性组合系数的选取主观性过强，本文基于一致性分析引入Spearman秩相关系数代替组合系数[29]，同时采用TOPSIS评估模型克服使用单一标准造成评估结果不够全面的缺点，客观反应对象的真实情况并极大减小了评估结果相同的概率[30]。本文评估方法的步骤如图4所示：1)采用灰色关联度分析法(grey relation analysis，GRA)对指标原始数据进行规范化处理；2)利用反熵权法和G1法组合赋权法确定各指标综合权重；3)构建加权矩阵并利用TOPSIS评估对象的优劣。

图4 综合评估模型步骤框图Fig.4 Step diagram of comprehensive evaluation model

3.1 原始数据预处理

本文采用GRA对能效指标进行规范化处理，选取不同决策方案中正向指标最大值为基准值，逆向指标中最小值作为基准值，区间指标取最优值为基准值。针对m种方案、n项指标的体系其规范化矩阵En×m中元素求取如式(26)所示。

(26)

式中：x0为能效指标基准值；xi(k)为i方案第k项能效指标原始值，i=1,2,…m；ζ为分辨系数一般为0.5。

对规范化矩阵进行归一化处理得到中转矩阵，其元素求取如式(27)所示。

(27)

式中pij为中转矩阵中第i行第j列元素。

3.2 指标权重的确定

3.2.1 G1法确定主观权重

采用G1法无需一致性校验，其步骤如下。

1)选取专家且确定指标集X={x1,x2,…,xn}各指标序关系，x1≻x2≻…≻xn。

2)确定相邻指标间的重要程度，设专家对指标xk-1与xk重要程度之比。

(28)

式中：ωk为第k项指标的主观权重；rk的取值依据指标标度表4所示。

表4 指标标度表Tab.4 Index scale Table

3)确定各指标主观权重系数。

(29)

式中ωn为指标集中xn的客观权重。

4)专家组权重确定。

(30)

3.2.2 反熵权法确定客观权重

设有m种多指标决策方案，每个决策方案包含n项指标，则求取系统的熵值h得

(31)

式中pij为方案i中第j项指标的归一化值。

与传统熵值特征不同，本文提出的反熵值与指标间的差异程度成正相关，即指标的差异性越大，反熵值越大，该指标权重系数越大。针对交直流配电网能效多指标体系，反熵的定义为

(32)

各指标的客观权重表示为：

(33)

3.2.3 基于一致性分析的组合赋权方法

为避免权重组合系数选取的盲目性，引入Spearman秩相关系数量化多种赋权方法之间的一致性，其计算公式如下：

(34)

第i种赋权方法的平均一致性为：

(35)

式中：m为采用的赋权方法种类数。将各赋权法的一致性系数作为组合系数获得最终权重。

(36)

式中Wi为第i项指标未考虑一致性系数的综合权重。

3.3 基于TOPSIS的综合评价模型

利用已经求得的规范矩阵E和综合权重向量W构造加权矩阵Y。

(37)

式中：ξi为各指标对应的各方案的规范值向量；ωi为各指标的权重向量。

根据逼近理想解排序法，确定加权矩阵的正理想解Y+和负理想解Y-。

(38)

式中：j+为效益类指标本文指能效正向指标，j-为成本类指标本文指能效负向指标。针对区间指标选取最靠近中心的指标值为正理想解，最远离中心为负理想解。

计算第i个评估对象到正理想解和负理想解的欧氏距离为：

(39)

(40)

计算各评估对象的综合评估指数：

(41)

按照综合评估指数fi大小依次排序，fi越大表示该评估对象表现越优。

4 算例分析

本文通过对文献[5 - 7]相关算例进行改造，形成具有代表性的四个模拟算例，分别为：传统交流配电网Z1,旧城改造后引入直流线路的交直流配电网Z2，高直流供电容量占比、源荷波动极低的优质电力园区Z3，高DG渗透率的交直流配电网Z4。本文基于源网荷建立能效指标体系，并采用G1-反熵权组合赋权法确定权重，利用TOPSIS模型评估各配电网能效水平。

4.1 指标预处理

根据步骤框图，首先对4个模拟算例中19个指标进行指标预处理，计算求得对应的初始值、基准值、归一化后的值详见附表1。其中区间指标线路负载率和变压器负载率选取经济运行点作为基准值处理；用GRA法根据公式26对指标原始集进行规范化处理，求得指标集的规范化矩阵E19×4见附表2。上述各矩阵计算结果均保留4位小数以方便计算。 图5为4个算例19项指标规范化后的雷达图，通过图中19项指标围成几何图形的面积，可以粗略的反应各配电网的能效水平。

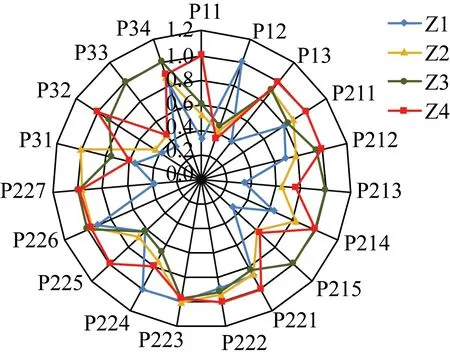
图 5各项指标规范化Fig.5 Normalization of indicators

4.2 主客观权重计算结果分析

主观权重计算依赖专家组科学客观的建议，本文算例采纳5位长期研究交直流配电网能效领域专家的打分情况，各层级序关系评价结果如表5所示。用1,2,3…来描述指标间的序关系，如：二级指标中231代表序关系为S2>S3>S1。专家根据序关系对相邻指标间的相对重要程度打分结果如表6所示。相对重要程度采用A,B,C…来表示(依次代表1.0,1.1,1.2…)，如：二级指标中FC代表相对重要程度r2=S2/S3=1.5;r3=S3/S1=1.2。

结合各专家打分情况可知，专家组对于序关系的评价略有不同，而对相对重要程度打分情况相对严苛，最高ri值为1.7，保证了各层间的权重系数档次充分拉开，同时整体而言专家对各层级指标序关系的打分相对接近，说明专家经验的相似性。

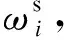
根据表7所示，指标P11、P12、P213、P33采用G1法计算的主观权重较综合权重偏高，这是由于各专家个人的研究内容、领域认知以及经验有所差异，导致对主观权重影响较大。结合公式31采用熵权法求得表7中熵权权重。对比客观权重可知电源侧、负荷侧各项指标以及电网侧P213、P215、P227的熵权权重偏低，这是由于指标差异较大造成的，其余各指标由于指标差异化较小权重系数相近，传统熵权法计算结果因差异化大指标权重小，差异化小指标权重大无法拉开评价差距，重要指标得不到突显导致失效。

表5 序关系专家打分表 Tab.5 Scoring Table of relationship experts

表6 相对重要程度打分表 Tab.6 Scoring Table of relative importance

表7 交直流配电网各项指标权重 Tab.7 Index weights of AC and DC distribution networks

结合上述分析，采用G1法避免了AHP法所需的一致性校验，简化计算；采用反熵权法克服了传统熵权法因灵敏度过高而导致指标失效的缺陷。综上所述，采用G1-反熵权法的组合赋权方法既采纳了专家对指标重要程度的分析，也保留了数据自身的内部信息，相比已有的方法具有明显的优势。

指标权重结果如图6所示，其中综合权重较大的包括：电源侧P11、P12和P13；负荷侧P31、P32、P33，突出电源侧和负荷侧指标在评估过程中的重要性。尤为突出的是电源侧DG容量占比P11和负荷侧高损设备容量占比P32的权重，证明两者对能效水平具有较高的影响。另DG出力波动率P12、负荷总波动率P31以及节能率指标P33指标权重较大，然而现有指标体系忽略了这类指标的重要程度，导致评价结果不过全面客观，本文基于源网荷构建指标体系，可兼顾源荷侧重要指标的考虑。

图6 各指标综合权重图Fig.6 Comprehensive weight chart of each index

表8 各项指标正、负理想解 Tab.8 Positive and negative ideal solutions of each index

此外，电源侧DG容量占比P11、DG出力波动率P12，电网侧供电半径P212、直流供电容量占比P312；负荷侧高损设备容量占比P32、节电率P33在各指标层级中相对较大，被专家评价为相对重要的指标，结合附表1可知上述指标初始值差异较大，故指标主客观权重值较大。而对于综合权重较小的指标是由于专家评价下的相对重要程度低，且各配电网该能效指标数据差异小，所以主客观权重小；电网侧运行指标层级由于指标数目较多且又处于较低层级，导致指标的综合权重较小，因此电网侧指标数目不易过多，为防止过多指标的引入采用主成分分析法适当筛选掉成分相似度的指标，降低指标间的相关性[31]，此处不再累述。

4.3 TOPSIS综合评估分析

由规范化矩阵E和综合权重W通过式(33)构造加权规范化矩阵。依据公式38选取4个评估对象中各指标正理想解或负理想解。另设交直流配电网在线路和配变负载率均为70%时实现经济运行， 线路负载率P222、变压器负载率P223可依此条件在规范化矩阵E选取正负理想解，结果如表8所示。

表9 各配电网相对贴近度Tab.9 Relative closeness of distribution networks

直接采用函数法即综合权重矩阵W与规范化矩阵E相乘所获得各评估对象的综合得分与采用TOPSIS评估结果如图7所示，传统的函数法存在得分区分度较小的可能，这是由于指标数值差异小和采用单一标准造成评估不够准确；而采用TOPSIS评估得分客观可靠的依据各项指标数值的欧氏距离来表示，很好地克服上述评估结果不够全面的缺点,并极大减小了评估结果相同的概率；同时贴近度的大小反应评估对象趋于理想状态的程度，反应系统的整体能效水平。

图7 各配电网能效相对贴近度Fig.7 Relative closeness of energy efficiency of each distribution network

相比较现有能效评价指标体系，本文创新点是考虑从源网荷3方面建立能效评价指标体系，评估过程中更加注重现有指标体系缺乏对电源侧与负荷侧指标的考虑，突出源荷波动率等电源侧和负荷侧多因素对配电网能效的影响, 并进一步简化对电网侧指标的分析，使得评估的角度全面而又不繁琐，更加客观。

5 结论

本文考虑从电源侧、电网侧、负荷侧三个方面构建了一套适用于交直流配电网共计19项指标的能效评价体系，建立了G1-反熵权法与TOPSIS综合评价模型，通过算例分析得到以下结论。

本文采用G1-反熵权法的组合赋权法既采纳了专家对指标重要程度的分析，也保留了客观原始数据自身的内部信息，同时引入Spearman秩相关系数代替传统组合系数，避免评价结果主观性过强，同时采用TOPSIS综合评估充分反映各方案之间的差距，极大减小了评估结果相同的概率。

实例结果表明了交直流配电网的能效水平显著高于传统交流配电网；高DG渗透率、PET的引入也将提高配电网能效水平；以及全面考虑源荷波动率等电源侧和负荷侧指标的必要性，符合理论分析的结果验证了综合评估模型的合理性。

本文基于源网荷构建了交直流配电网能效评价指标体系以及评价方法，为交直流配电网进一步科学的规划、建设和管理提供一定的参考价值。