基于区间Orthopair模糊距离测度的VIKOR多属性决策方法

舒慕华，王思宇，林志超，周礼刚，肖 箭

(安徽大学 数学科学学院，合肥 230601)

多属性决策(MADM )是指存在多个备选方案时，如何选择一个最满足一组评价指标的问题，是当代决策科学的一个重要组成部分.多属性群决策问题的实质是在多个属性和多个决策者的共同参与下，对备选方案进行择优或者排序的过程.一些经典的多属性决策方法常常得到广泛运用与研究，例如TOPSIS方法，PROMETHEE方法，ELECTRE方法，VIKOR方法等.VIKOR方法是Opricovic教授[1]提出的一种基于折衷规划的排序方法，主要用于解决复杂并且含有多准则优化问题.随后，Opricovic和Tzeng教授[2]进一步比较了这四种经典的多属性群决策方法，认为VIKOR方法不仅考虑了最大化的群效用并且也追求了个体遗憾的最小化，且引入了决策系数，充分考虑到了决策者的主观偏好，保证决策更加合理性与准确性[2].

在多属性群决策问题中，常常需要决策者提供决策信息，但是在实际问题中，由于事物本身的模糊性、不确定性以及专家或决策者知识结构和个人偏好等主观因素的影响，对表现出一定程度犹豫以及含有不确定信息的决策问题，专家或决策者需要做出清晰准确的决策十分困难.文献[3]中Zadeh提出模糊集的概念[3]来描述对象的不确定性，之后许多学者都在研究推广模糊集理论，并运用于不同的决策场景.Zadeh本人又提出了区间模糊集和2-型模糊集的概念[4].Atanassov将模糊集推广到了直觉模糊集(IFs)[5]，并用隶属度与非隶属度来表征研究对象，满足两者之和小于1的限制.

随着社会信息的多元化及复杂化交融，Yager研究发现毕达哥拉斯模糊集仍然无法适用于更加复杂的多元问题.因此，Yager基于直觉模糊集以及毕达哥拉斯模糊集理论知识进一步提出了q-rung Orthopair模糊集(q-ROFs)的概念[9]，其中要求其隶属度与非隶属度的q次幂之和不超过1.此时，可以看出，直觉模糊集和毕达哥拉斯模糊集都是q-rung Orthopair模糊集(q-ROFs)的特殊情况(q=1和q=2).并且由于q次幂的广泛性，q阶Orthopair模糊集合可以扩大模糊信息的范围，放宽限制条件，为研究理论以及解决问题带来了便利.很多专家和学者都基于q-rung Orthopair模糊集(q-ROFs)在该领域不断探索和研究.Du[10]提出了一个功能测量两个q阶Orthopair模糊集合，介绍了q阶Orthopair的相关系数以及相关系数有界和无界连续的模糊集域.Liu和Wang[11]提出了q阶Orthopair模糊权重平均运算和q阶Orthopair模糊权重几何运算如何去解决多属性决策(MADM )问题.Wen[12]提出了Minkowski型距离测量，并讨论其关于多属性群决策问题的实际应用.由于目前对构造区间Orthopair模糊距离测度的多属性决策模型研究较少.因此，本文采用区间q阶Orthopair模糊集合处理VIKOR方法中的不确定性的多属性决策问题.

距离测度不仅是模糊集的理论中的重要概念，也是VIKOR法中非常重要的理论基础.经典的折衷规划法就是基于距离测度来决定特定解与理想解的贴近度.Papakostas[13]和Xu[14]等很多学者对已有的距离测度以及相似性测度进行了研究和对比.本文基于Wang[15]提出的一种新的直觉模糊距离测度来体现直觉模糊集的信息特点，提出一种基于区间Orthopair模糊距离测度，并更好的运用到VIKOR方法当中解决多属性决策问题.该方法运用新的区间Orthopair模糊距离测度计算VIKOR法中的群体效用和个体后悔度进而得到决策结果，并对结果进行合理并有效的讨论与分析.

1 预备知识

定义1[16]设X是一个非空有限集合，X上的直觉模糊集(IFs)可以定义为

A={x,μA(x),vA(x)|x∈X}

(1)

其中：函数μA(x)∶X→[0,1]和vA(x)∶X→[0,1]分别表示元素x属于X的隶属度和非隶属度，并且满足约束条件0<μA(x)+vA(x)≤1，则直觉模糊集的犹豫度为：

πA(x)=1-μA(x)-vA(x)

(2)

显然πA(x)∈[0,1]，表示X中元素x属于A的犹豫度或不确定度.

定义2[17]设X是一个非空有限集合，则X上的Orthopair模糊集(OFS)可以定义为

O={x,μO(x),vO(x)|x∈X}

(3)

其中：函数μO(x)∶X→[0,1]和vO(x)∶X→[0,1]分别表示元素x属于X的隶属度和非隶属度，并且满足约束条件0<(μO(x))q+(vO(x))q≤1，(q≥1)，则Orthopair模糊集的犹豫度为：

πO(x)=(1-(μO(x))q-(vO(x))q)1/q

(4)

显然πO(x)∈[0,1]，表示X中元素x属于o的犹豫度或不确定度，为了方便，称(μO(x),vO(x))为Orthopair模糊数(OFN)，表示为(μO,vO).

其中:当q=1时，O为直觉模糊集；当q=2时，O为毕达哥拉斯模糊集;当q=3时，O为Fermatean模糊集.

区间Orthopair模糊集是对 Orthopair模糊集的推广.

定义3[18]设X为一个非空有限集合，则X上的区间Orthopair模糊集(IOFNS)可以定义为：

(5)

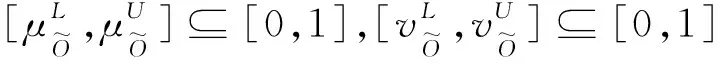
(6)

1)加法

2)乘法

3)数乘

4)幂

容易证明，区间Orthopair模糊数(IOFNS)有如下的运算律[18]：

(7)

为记分函数，称

(8)

为精度函数.

同时，文献[19]还给出了区间Orthopair模糊数排序的方法.

2 一种新的区间Orthopair模糊距离测度

(9)

(10)

3 基于新的区间Orthopair模糊距离测度的VIKOR法

(11)

表示第k名决策者对第i个方案关于第j个属性给出的评价结果，通过区间Orthopair模糊数表示.基于新的区间Orthopair模糊距离测度的VIKOR法具体步骤如下：

i=1,…,m,j=1,…,n,k=1,…,l

(12)

(13)

步骤3：确定每个方案在每个属性的权重ωij.

根据式(14)计算第i个方案在第j个属性的权重ωij，其中Eij为第i个方案下在第j个属性的熵：

(14)

其中:

(15)

(16)

(17)

步骤5：计算群效用值Si和个人遗憾值Ri.

根据式(18)计算群效用值Si

i=1,…m,j=1,…,n

(18)

根据式(19)计算个人遗憾值Ri

i=1,…,m,j=1,…,n

(19)

步骤6：计算折衷评价值Qi.

设γ为决策系数，表示群效用最大策略的权重，1-γ表示个体遗憾的权重，且γ∈(0,1).若γ∈(0,0.5)，则主要考虑个体遗憾值；若γ∈(0.5,1)，则主要考虑群效应.根据式(20)计算折衷评价值：

Qi=γSi+(1-γ)Ri,i=1,2,…,m

(20)

步骤7：对各方案进行排序.

根据群效用值Si、个人遗憾值Ri和折衷评价值Qi对各方案进行排序，排序方法如下：

将备选方案分别根据群效用值Si、个人遗憾值Ri和折衷评价值Qi从小至大排序.把折衷评价值Qi从小至大排序，满足以下两个条件的第一个备选方案A(1)为最优方案.

条件1：可接受决策的优势性.设A(2)为按照折衷评价值Qi排序第二的方案，满足Qi(A(2))-Qi(A(1))≥DQ有：

(21)

条件2：可接受决策的稳定性.首先通过折衷评价值Qi排序后为第一的备选方案需要满足其在群效用值Si和个人遗憾值Ri中的升序也为第一，即为从群体效用值来看，最优的备选方案比次优方案的更优，或者从个体妥协值来看，最优的备选方案比次优方案的小.

若一个备选方案不能满足上述的两个条件时，于是说明有多个备选方案非常接近，因此以下提出一个妥协方案集合：

1)若不满足条件1，妥协方案集合A(1),A(2),…,A(t)，其中t满足不等式：Qi(A(2))-QiA(1)≥DQ的最小自然数.

2)若只不满足条件2时，排序的第一方案和第二方案，均为最优的方案.

4 实例分析

现有一上市公司在为某投资项目选取方案，他们收到公司给出的四个备选方案A1，A2，A3和A4，为了选择一个最优方案，公司准备从：C1利润值，C2风险性，和C3可实行性三个方面来对四个备选方案进行决策.公司的四名决策者D1，D2，D3和D4构成评审组来对四个方案进行综合评价和决策分析，最终进行最优方案的确定.

不失一般性，我们取q=2进行分析，决策步骤如下.

步骤1 决策者提供的评价矩阵表达了对于备选方案Ai在属性Cj的隶属度和非隶属度.此时用区间Othopair模糊数表达相关信息，评审组四名决策者对每个属性下的备选方案进行评价，对应的评价矩阵见表1～4.

表1 决策者D1提供的评价矩阵

表2 决策者D2提供的评价矩阵

表3 决策者D3提供的评价矩阵

表4 决策者D4提供的评价矩阵

步骤2 根据式(13)计算综合评价矩阵见表5， 四名决策者的权重根据公司股权的分布来确定为：W=(W1,W2,W3,W4)T=(0.20,0.25,0.25,0.30)T.

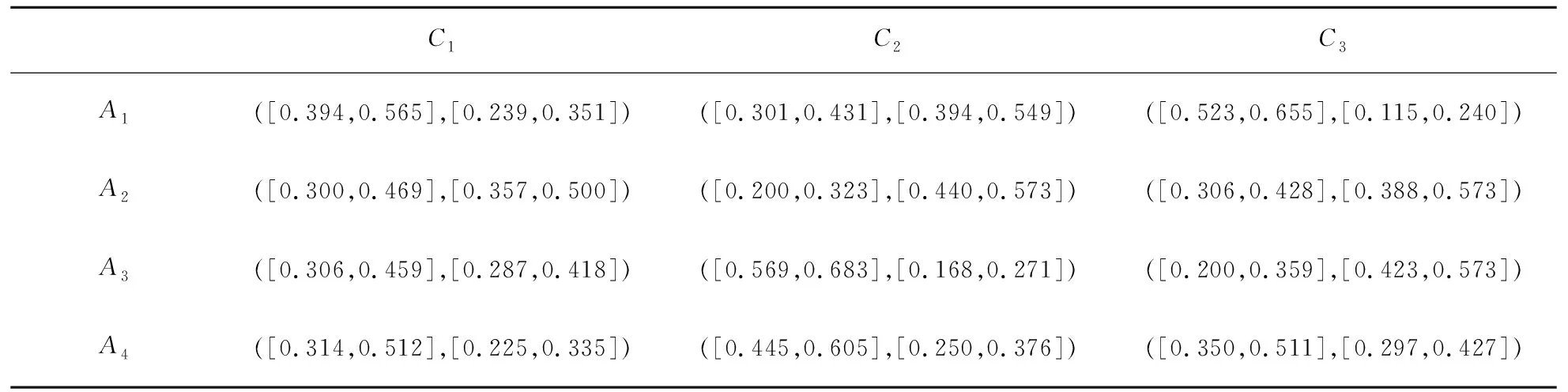
表5 综合评价矩阵

步骤3 根据式(14)、(15)计算出每个方案下的各属性权重矩阵见表6.

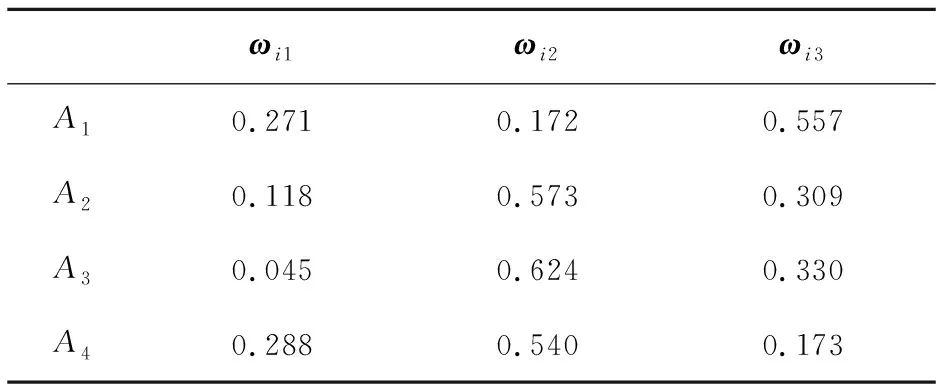
表6 各方案下的属性权重矩阵

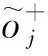
步骤5 由式(17)、(18)计算群效用值Si和个人遗憾值Ri得：

S1=0.133，S2=0.965，S3=0.358，S4=0.315.

R1=0.133，R2=0.573，R3=0.331，R4=0.151.

步骤6 不失一般性，令γ=0.5，由式(19)计算折衷评价值Qi得：

Q1=0.133，Q2=0.769，Q3=0.344，Q4=0.233

步骤7 对群效用值Si、个人遗憾值Ri和折衷评价值Qi进行排序得：

Si：A1A4A3A2，

Ri：A1A4A3A2，

Qi：A1A4A3A2

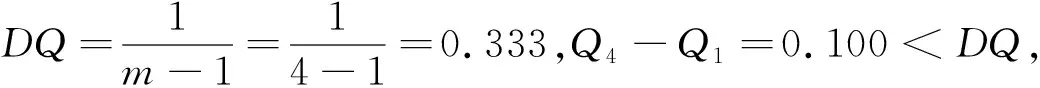
当γ=0.5为了验证计算结果对参数q的敏感性，取q=1,2,…,10进行敏感性分析，折衷评价值Qi随着q值的变化情况如图1.

图1 折衷评价值Qi随着q值的变化图Figure 1 Change of trade-off evaluation value with Qi value q

依据图1和通过python软件的计算结果，由区间Orthopair模糊距离测度的VIKOR方法计算可得：当q∈[1,4.309]时，备选方案的排序为A1≻A4≻A3≻A2，则可知A1是最优方案.当q>4.309时，备选方案的排序为A1≻A3≻A4≻A2，此时A3和A4的排序结果发生了改变，但是A1仍是最优方案.

当q=2为了验证计算结果决策系数γ的敏感性，取γ=0.1,0.2,…,1.0进行敏感性分析，折衷评价值Qi随着决策系数γ的变化情况如图2.

由图2可以看出，当决策系数γ∈(0,1)时，备选方案的排序均为A1≻A4≻A3≻A2，则可知A1是最优方案.

图2 折衷值Qi随着决策系数γ的变化图Figure 2 The trade-off value Qi as a function of the decision coefficient γ

对于多属性群决策问题中，影响方案排序的重要因素是属性权重.本文基于区间Orthopair模糊距离测度提出的VIKOR多属性决策方法是一种客观有效的方法，且有以下特点：1)根据区间Orthopair模糊信息存在不确定性和不具体性，本文提出新的区间Orthopair模糊距离测度综合考虑了区间隶属度，区间非隶属度和犹豫度，不仅反映了参数值之间的差异，而且考虑了区间Orthopair模糊信息的波动性，从而能够更准确的表达不确定性信息;2)相比文献[20]，本文通过熵理论来确定备选方案各属性的权重，该法确定属性的权重能够减少主观随意性，从而使得决策结果更加客观合理.

5 结 语

本文在新的模糊距离测度基础上，提出一种基于区间Orthopair模糊距离测度的VIKOR多属性决策方法，并进行了实例分析验证了该方法的真实性和有效性.通过提出熵权模型求解不同属性权重，并运用到模糊距离测度来计算VIKOR方法中的折衷评价值等从而进行有效决策.与经典的VIKOR方法相比，本文的优点在于提出了一种新的模糊距离测度考虑到区间Orthopair模糊环境下信息的波动性和不具体性，更有效地反映了区间Orthopair模糊数的信息特点，并且通过参数q和决策系数γ的变动可以反映决策结果的灵敏性.