具有不可靠修理设备的退化系统维修策略研究
李延玲,傅 华
(1.青海民族大学 数学与统计学院, 西宁 810007; 2. 福建警察学院 福州 350007)
近年来,随着经济的发展和电子产品的广泛应用,对系统可靠性的研究变的越来越重要,许多学者在这方面有大量的研[1-5],为了提高系统的可靠性,系统的维修策略成为了重要的研究内容[6-9],本文提出了一个更一般的单部件退化可修系统,假设修理设备在修理期间也可能会发生故障并且在故障之后会立即替换一个新的修理设备继续修理故障系统.另外,由于修理工需要检查故障原因或不在岗等原因系统的修理将会被延迟,特别的,和之前文献不同的是修理时间服从一般分布并且考虑了修理设备的替换时间,在这些假设条件下[10-12],我们通过几何过程及补充变量法建立了系统的数学模型,利用Laplace变化给出了系统的可用度,由于系统是退化的可修系统,经过长时间的工作系统的可用度将趋于零[13-15],为了提高系统的可靠性以及节省系统的所需费用,进一步研究了基于故障次数的N策略替换.
1 数学模型
首先,给出该系统的基本假设.
假设1 系统是一个单部件系统,初始时刻系统是全新的并处于工作状态.
假设2 假设系统部件故障后不能修复如新,第(n-1)次修复完成与第n次修复完成之间的时间间隔称为系统的第n个周期.设Xn和Yn分别表示系统在第n个周期中的工作时间和修理时间,其分布函数分别为:
Fn(t)=F(an-1t)=1-exp(-an-1λt),
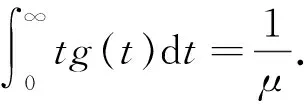

假设4 假设系统故障后不能够立即修理,设Wn表示系统在第n个周期中的延迟修复时间,其分布函数为H(t)=1-exp(-θt)(θ>0).
假设5Xn,Yn,Wn,Un,Vn,(n∈N)均是相互独立的.
通过如上假设,可以分析得出系统可能的相关状态.
状态0:t时刻,系统正在工作,修理设备处于正常状态.
状态1:t时刻,系统发生故障处于延迟修复状态.
状态2:t时刻,修理工正在修理故障系统.
状态3:t时刻,修理设备发生故障,故障系统等待修理.
下面引进一些补充变量:
设S(t)=k(k=0,1,2,3)表示系统在t时刻处于状态k,I(t)=j(j∈N,t≥0)表示在t时刻系统处于第j个周期,Y(t)与Z(t)分别表示系统在t时刻已经用去的修理时间和修理设备更换时间.
利用以上随机变量我们给出系统所有可能状态的概率及概率密度函数.
Pij(t)=P{S(t)=i,I(t)=j}(i=0,1.j=N)
p2j(t,y)dy=P{S(t)=2,y≤Y(t) dy,I(t)=j}(j=N) p3j(t,y,z)dz=P{S(t)=3,z≤Z(t) dz,I(t)=j,Y(t)=y}(j=N) 通过分析在比较小的时间段内系统的状态变化建立了系统的偏微分方程组. 当j=1时: (1) 当j>1时: (2) 初始条件: (3) 进一步,由式(2)可以得出该系统所有可能状态的概率满足如下规范性条件: 该系统在时刻t的可用度是指系统在时刻t正常工作的概率,即 其Laplace变换为 由Tauberian定理可知系统的稳态可用度为 由方程(1)和(2)及初始条件有: (4) 由方程(4)有: (5) 由式(5)可知 从而有 因此,系统的稳态可用度为 上式说明,该退化系统在经过长时间的工作之后会变的完全不可用,因此系统的费用可能会更高,因为退化系统经过多次修复之后,修理的费用会比系统的收益更高.从经济角度出发,我们考虑基于系统故障次数的N策略替换,主要给出系统平均费用的精确表达式C(N),进而得到使得C(N*)最小的最优替换策略N*,也就是说,当系统的故障次数达到N*时不再修理,会替换一个全新系统继续工作. 首先,在之前假设的基础上需要增加如下两个假设条件. 假设6 设对该退化系统实行基于系统故障次数的N策略替换,就是指当系统的故障次数达到最优替换次数N*时,系统将会被一个全新的系统替换. 假设7 设cr,cw,r,cf分别表示系统的修理费用, 系统正常工作时的收益,系统的替换费用以及修理设备的替换费用. 其次,设τ1为系统的第一次更换时间,τn为系统第(n-1)次更换完成与第n次更换完成之间的时间间隔, 进而{τ1,τ2,…}形成了一个更新过程, 两次连续更换间的时间间隔称为一个更新周期. 由更新理论给出系统在N策略下系统平均费用的精确表达式C(N): (6) 其中:D和W分别表示在一个更新周期内的平均费用和平均长度, 由系统的工作进程有: (7) 其中:pi表示一个更新周期内系统修理设备的故障次数, 则pi的概率分布为[10]: 从而有 (8) 由式(8)及系统假设有 (9) (10) 最后将式(9)、(10)带入式(6)便得到系统在N策略下平均费用C(N)的精确表达式: (11) 进一步,为了说明系统最优替换策略N*的存在性与唯一性,本文给出如下相关参数的参数值: a=1.15,λ=0.3,μ=0.3, α=0.06,β=0.2,θ=0.4 p=0.4,q=0.6,Cr=20, Cf=0,Cw=300,r=2 500 将以上参数带入式(11)得表1. 表1 系统的平均费用率C(N) 从表1可以看出系统的最优替换策略N*=8存在且唯一,相应的费用C(N*)=-32.7最少, 也就是说, 当该退化系统的故障次数达到8次时, 我们会更换一个全新的系统 , 此时系统花费的费用最少. 本文主要考虑了一个修理设备可更换的单部件退化系统,修理时间服从一般分布,建立了系统的偏微分方程,利用Laplace变化讨论了系统的稳态可用度,从其表达式发现系统的可用度趋于零,这也说明对与退化系统而言经过长时间的工作之后系统将完全不可用.因此,为了提高系统的可靠性及节省系统所花费用,进一步讨论了基于故障次数的N策略替换,最后给出具体参数进一步验证了最优策略N*的存在性与唯一性.2 系统的可用度


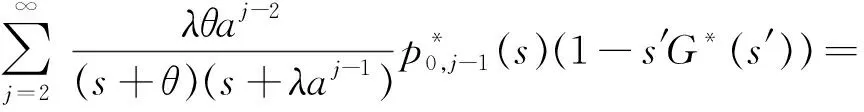
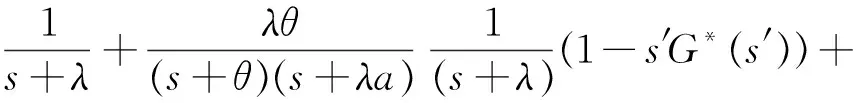
3 N策略

4 结 语

