基于最小二乘法对GM(1.1)模型的研究及应用

孙 冲，吴天庆，王 虹，刘 震

(1.陆军炮兵防空兵学院 基础部数学教研室,合肥 230000；2.宿迁学院 文理学院, 江苏 宿迁 223800；3.陆军炮兵防空兵学院 供应保障处,合肥 230000；4.郑州工商学院 工学院, 郑州 451400)

1952年，Markowitz[1]首次提出M-V投资组合理论，为研究现代投资组合选择理论奠定了基础.但是在实际应用中，很多数据只用一个精确数表示并不符合实际.在金融市场中存在不确定性问题，如股票价格、换手率等.为了解决不确定的问题，1965年Zadeh[2]提出了Fuzzy集的概念，随后一些学者[3-4]基于模糊决策理论对模糊收益下的投资选择模型进行了研究，建立了模糊投资组合选择模型，其研究结果在一定程度上弥补了传统M-V模型的不足. 但是，在投资决策的研究过程中忽略了决策之间的优劣问题，依然在模糊决策中利用数学期望值对期望收益率进行测度，仍存在个人主观性的问题．实际问题中，针对少数据、贫信息的不确定预测问题，灰色系统理论中对于少样本的预测方法应用相当广泛．其中GM(1.1)模型是灰模型中的核心模型，而且对于少数据短期预测精度很高．随后一些学者[5-13]利用原始数据一时间段的平均值进行M(1.1)预测，在预测过程中则丢失了很多信息，对决策的制定不利[14-15].本文利用最优解构造了区间模糊数的整体GM(1.1)预测模型，对未来收益率的区间模糊数进行整体预测，提高对未来收益率进行测度的精度.基于区间数建立模糊投资组合选择模型，并基于区间数的满意度进行优化，得到单目标规划模型.实例分析证明模型具有一定的柔性和有效性.

1 区间模糊数的定义方程

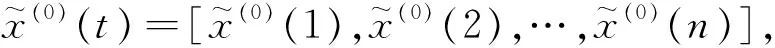
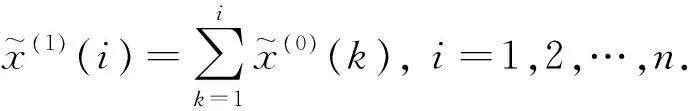
定义2[14]模糊数GM(1，1)模型的定义方程为:

其中：a为清晰数.

根据定义2得区间模糊数GM(1，1)模型的定义方程为:

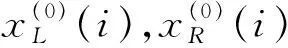
则可以构造方程组为：

则方程组的解为：

i=2,3,…,n.

2 区间模糊数的预测模型

对于线性方程的解分为无解、有唯一解、有无穷多解以及最优解.而对于方程的个数远大于未知量的个数时，如：

即AX=b.按下列步骤求解方程组：

1)对于方程组AX=b，可同时乘以AT即可得到ATAX=ATb，

2)对于方程组ATAX=ATb，可同时乘以(ATA)-1即可得到X=(ATA)-1ATb.

则方程组的最优解为：

当取a为a1、a2的加权平均值时，即a=αa1+βa2，其中α+β=1.则可以得到区间模糊数的预测公式为：

定义4[14]区间数A可表示为A=〈m(A),ω(A)〉为区间数A的中点和半径，其中：

3 建立模糊选择模型

设n个证券,E(ri)为第i个证券的期望收益率;R0为期望收益率的下限;xi为第i个证券投资比例;V(ri)n×n为协方差阵.则在收益达到预期情况下，风险最小化的M-V投资组合为:

minV(ri)n×n

(1)

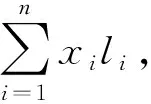
(2)

(3)

利用定义5可以得到下列结论.

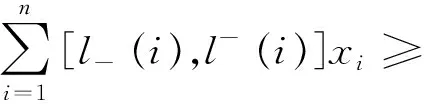
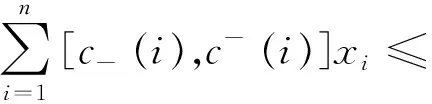
当给定投资者的满意度λ0时，则模型(3)可转化为模型(4)为：

(4)

4 实例分析

假设5种股票2019年3月～2019年7月的每月收盘价格以及换手率的区间范围,并预测收益率的区间、协方差阵区间以及换手率区间分别为：

预测收益率区间数为：

换手率的区间数为：

设交易成本区间数为：

由于卖空限制,因此利用Lingo软件求解得到最优解为:

x1=0.351 6,x2=0,x3=0,x4=0,x5=0.648 4.

给定满意度λ0=0.6时,模型为:

由于卖空限制，因此利用Lingo软件求解得到最优解为:

x1=0.462 5,x2=0,x3=0,x4=0,x5=0.537 5.

综上可得，若给定不同的满意度λ0，可得到不同的投资组合，证明模型具有一定的柔性，可以适合不同的投资者.