直流配网中飞轮储能的虚拟惯性控制策略

（山西大学电力与建筑学院，山西 太原 030000）

现代电力系统中电动汽车、大数据中心等直流负荷日益增长，分布式电源大规模接入，传统的交流配网由于其过多的逆变环节而造成的转换环节多、系统效率低等问题，已经无法满足现代电力系统的发展需求。直流配电网络不存在无功功率的损耗，更少的变流环节使得直流配网更容易消纳分布式电源，降低系统的控制难度、增加系统的供电可靠性[1-3]。

系统惯性的大小是交直流电网的显著区别之一[4]。传统的交流电力系统中，发电机与电网之间直接进行耦合，发电机较大的旋转动能为交流系统提供了惯性支撑，使其在扰动情况下电网更稳定。而直流配电系统为小惯性系统，直流侧等效电容值较小，此外，其消纳的分布式电源中，光伏发电系统惯性较低，风力发电系统受限于电力电子变换装置的隔离，需要辅以一定的控制策略[5]。较小的系统惯性造成直流系统在随机负荷及大扰动的情况下，容易引起直流电压突变造成减载运行。因此，利用直流配电网中电机的旋转动能及储能电池提高直流系统的惯性，是直流配电系统中需要解决的问题[6]。

目前，直流配电系统中，风力发电系统可通过MPPT曲线调整，提升系统等效惯性[7]。利用下垂控制策略对储能系统进行控制，也使得直流配电系统的等效惯性进一步提升[8-9]。针对下垂控制的不同优化策略可以充分发挥储能系统的惯性支撑能力[10]。

飞轮储能是一种基于机电能量转换的储能系统，系统中的旋转动能能够有效为系统提供惯性支撑，此外飞轮系统具有储能密度高、应用范围广、效率高、寿命长及无污染的特点，可以为直流配网更好地消纳分布式电源提供新途径[11-12]。

本文首先分析直流配网中虚拟惯性的概念，在此基础上分析飞轮储能系统对于虚拟惯性的支撑作用[13]，同时利用下垂控制对飞轮系统进行控制，提升其对系统的惯性支撑能力。提出新的下垂系数计算函数，通过虚拟惯性和下垂的协同控制改善直流配电网的稳定性。

1 系统构成

包含飞轮储能系统的光储直流配电网结构示意图如图1所示，主要由飞轮储能系统、光伏发电系统、负荷部分、并网变流器四部分组成。

图1 光储直流配网结构示意图Fig.1 Schematic diagram of optical storage DC distribution network

以无刷交流电机作为内置电机的飞轮储能系统[14]，经AC-DC整流器接入直流母线；光伏发电系统，经双向DC-DC变换器接入直流母线，运行于MPPT模式；并网变流器通过AC-DC变流器G-VSC与大电网相连。直流负荷通过AC-DC变流器与直流母线相连。

2 系统虚拟惯性特性分析

2.1 直流配电网惯性分析

在交流系统中，系统的惯性由惯性时间常数Hs表示为

式中：Ek为转子额定转速时储存的动能；SN为发电机的额定容量；J为转子的转动惯量；ω为转子的机械转速。

直流配电网惯性时间常数定义为额定电压下配电网直流电容存储能量全部释放所需要的时间。直流系统的惯性由惯性时间常数Hd表示：

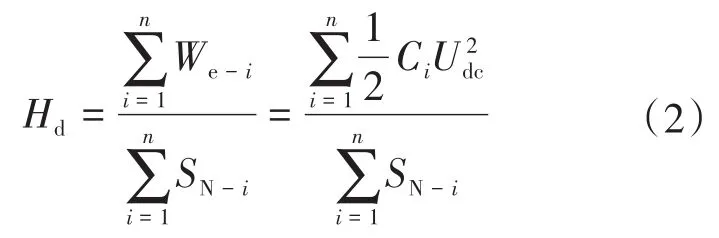
式中：We-i为直流电容Ci的储能；SN-i为第i个直流电容的额定容量;Udc为直流侧电压。

由式（2）可知，直流配网的惯性时间常数正比于直流侧电容，因而增大直流侧的虚拟电容可以增大系统惯性时间常数，其自适应惯性常数Hs可用系统的惯性时间常数Hdc表示为

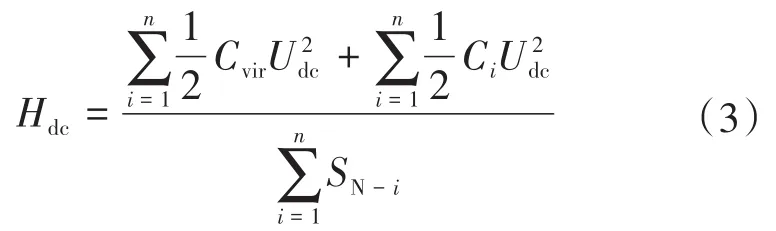
式中:Cvir为虚拟电容。

2.2 飞轮储能系统惯性分析

飞轮储能系统将能量以动能的形式储存在高速旋转的飞轮之中，其动能为

式中：JF为飞轮的转动惯量；ωg为飞轮旋转角速度。其能量释放的方式为速度的改变:

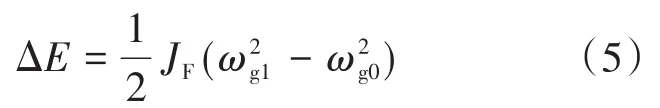
式中：ωg1为t时刻的旋转角速度；ωg0为初始时刻的旋转角速度。

当系统直流侧发生功率失衡导致直流电压扰动时，飞轮储能系统变流器直流侧电容充放电功率为

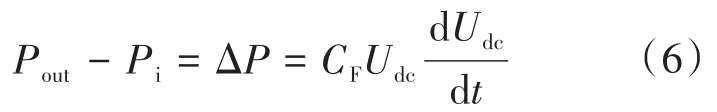
式中：Pout为直流电容出口侧功率；Pi为直流电容入口侧功率；CF为直流电容的大小。

飞轮储存或释放的功率为

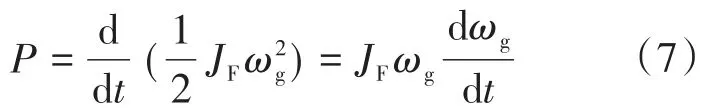
暂态扰动过程中，飞轮利用自身动能变化对系统的电压波动进行抑制，不计电机损耗的理想状态下，则直流母线电压变化转化为转速波动。联立式（6）、式（7）可得：

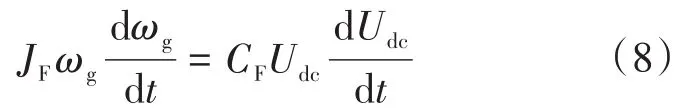
对式（8）两边进行积分可得:

式中：ωga，ωgb，Udca，Udcb分别为a，b时刻的飞轮机械角速度和直流母线电压。

取飞轮在b时刻电压额定值情况下的转速为额定转速，取ECN为额定电压下电容储存的能量，对式（9）进行标幺化处理，得：

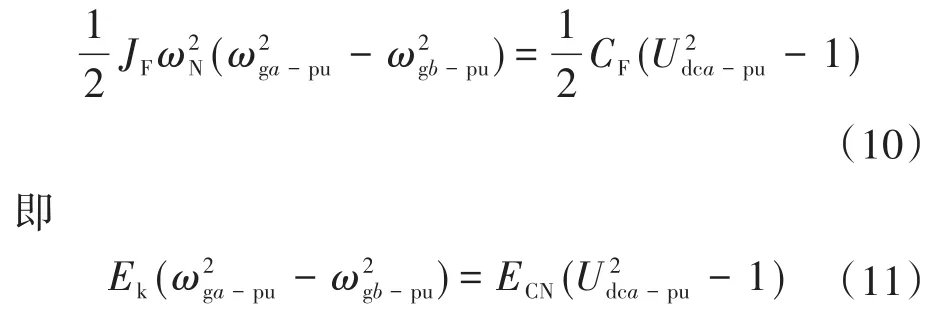
由式（11）可得，当改变飞轮的角速度，即储能系统在功率变化时以不同的转速波动承担功率变化。对式（7）进行拉氏变换得到

由以上分析得：系统受到扰动，因功率的缺额或过剩引起电压变化时，飞轮系统可以通过转速的控制以输出更多的功率对系统的惯性进行支撑。

3 飞轮储能系统外环协同控制策略

3.1 变下垂系数控制策略的优化

采用下垂控制时，储能的U—P特性曲线为

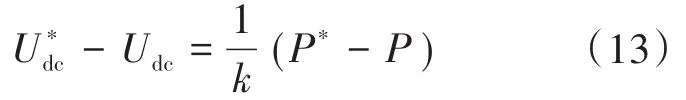
当dUdc∕dt变化较大时，应使下垂曲线更加平缓从而为系统扰动提供更多功率支撑。下垂特性曲线的斜率k为

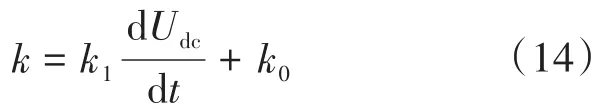
式中：k0为初始状态下的斜率；k1为变下垂系数函数关系中的比例系数。

则有：

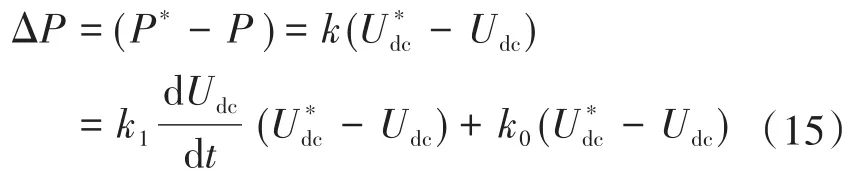
取变流器原稳态时直流侧电容输入端功率为Pi，输出端功率为Pout，改变下垂系数后输出功率为Pir，直流侧输出端功率为Poutr，则有：

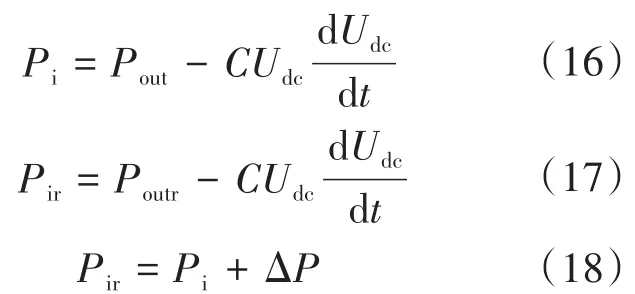
由式（18）可得：

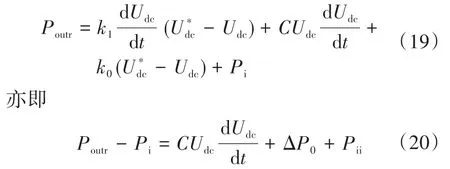
式中：Pii为变下垂系数比例常数虚拟出的功率；ΔP0为原特性曲线下功率的该变量。

取等效电容功率为Pvir，则有：

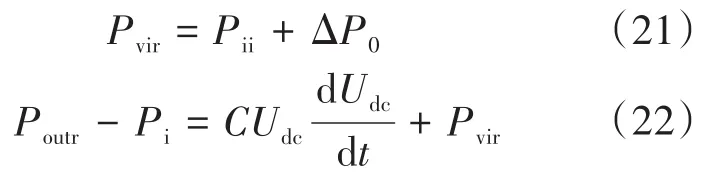
由式（22）可看出在电压变化时，改变下垂系数相当于在原直流侧虚拟出等效电容，且由式（19）至式（22）可得，可以通过改变k1改变变流器对系统的惯性支撑能力。当k改变时，下垂特性曲线的摆动情况如图2所示。

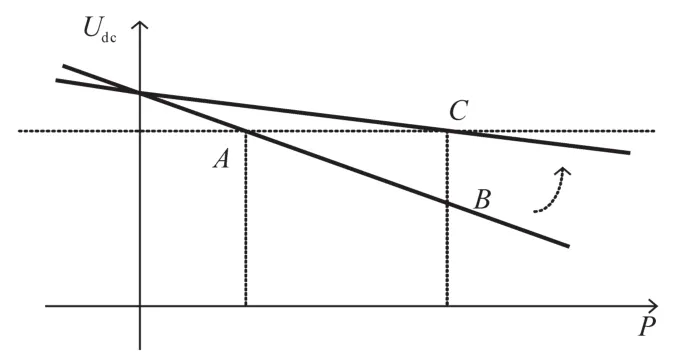
图2 下垂特性曲线摆动Fig.2 Pendulous characteristic curve oscillation

稳态时，系统运行于A点。当系统负荷突增或分布式电源出力突然减小时，若下垂特性曲线不改变，则系统功率差额逐渐减小至0，运行于B点;当利用式（14）进行下垂特性控制，此时（dUdc∕dt）<0，下垂特性曲线斜率减小，下垂特性曲线沿图2箭头所示方向摆动，功率差额不断减小，降低了Udc的下降速度，直至功率差额减小至0时，系统运行至C点达到新的稳态，此时（dUdc∕dt）<0，k=k0，下垂曲线斜率返回稳态时的值。同理，当系统负荷突减或分布式电源出力突然增大时，按照相同方法进行控制。

3.2 系统出力上下限分析

由上文分析可知，对于飞轮系统而言，系统释放或吸收的功率越大，其对直流母线电压的稳定作用越大，但对于飞轮吸收和释放功率时有：

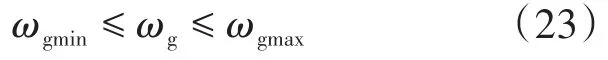
即对于飞轮系统释放其最大功率限制：

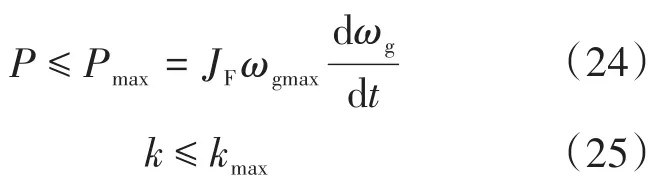
k的选取应当考虑系统直流母线电压的限值。飞轮系统功率、转矩和转速满足关系式：

当飞轮控制系统功率参考值较低时，ωg较低，当下一稳态系统需要较大功率时，由式（26）可知，其需要的转矩较大，可能会超过其最大转矩。因此系统的功率最小值受转矩以及系统最低转速限制。则有：

即，系统的下垂特性曲线的斜率最小值受直流母线电压波动限值和系统稳定运行的转速限制。

3.3 对于下垂特性曲线的改进方法

对于式（14）所提的一次函数进行变下垂系数的斜率算法，该函数计算简单，但是其在下垂控制中，并未完全发挥系统的惯性调节能力。

在下垂曲线系数函数的选择中，其函数在保证下垂系数不越限制的情况下，满足子区间内为单调函数，且向最值的收敛速度应尽可能的快，由此可以充分利用控制裕度，为系统提供惯性支撑。此外，在直流母线电压变化率为0时，下垂系数应等于初始值。对双曲正切函数，反正切函数收敛性进行对比如图3所示。

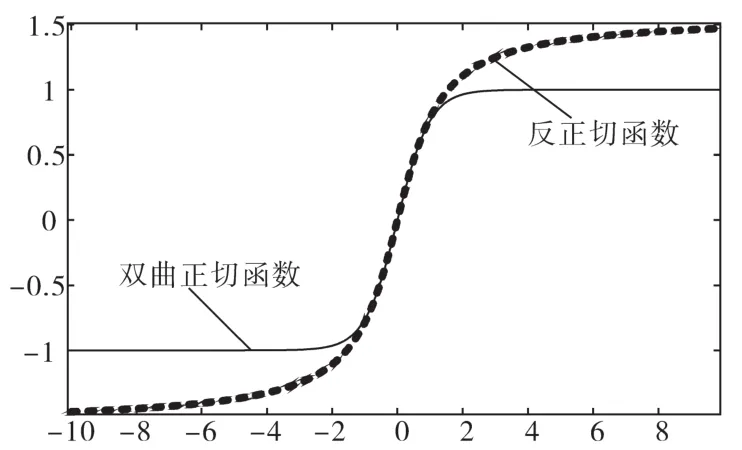
图3 函数收敛性对比图Fig.3 Comparison diagram of function convergence

如图3所示，相同系数下，双曲正切函数具有更好的收敛性。因此选择双曲正切函数对原下垂系数进行优化，可得新的动态下垂系数：

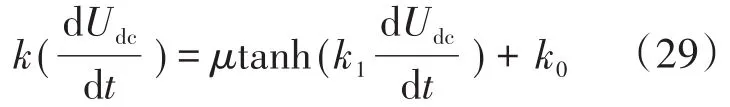
式中：μ为系数。

为保证系统的直流电压变化量不超过限制，其下垂系数不超过其限值。

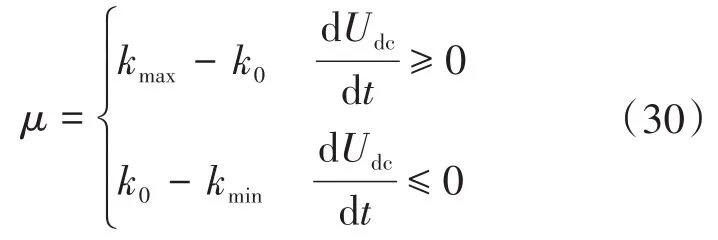
即新的动态下垂系数：

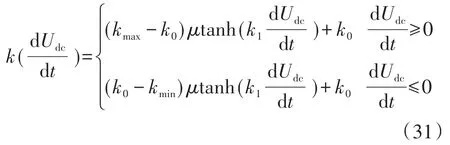
由式（31）得到的下垂系数k随电压变化率的函数图像如图4所示，当电压变化率较大时，其下垂系数k接近于限值，使得系统在保持最佳的惯性调节能力的基础上稳定运行，而下垂系数函数向最值具有良好的收敛性，使得系统在电压变化率增大时，能迅速地运行在最大惯性能力调节状态下，有效地避免了直流母线电压变化率较小时，系统的惯性调节能力较差的问题。

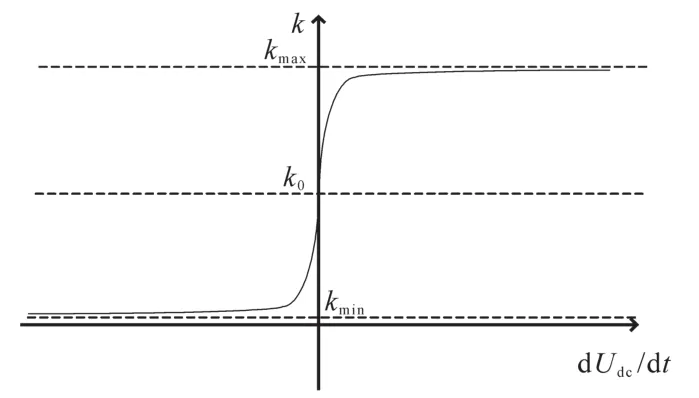
图4 下垂系数变化曲线Fig.4 Variation curve of sag coefficient

图4中k0取值讨论如下：当系统受到扰动时，（dUdc∕dt）≠0，系统的U—P特性曲线的下垂系数按照函数发生变化，直流母线电压减小时，k0趋于kmax；直流母线电压增大时，k0趋于kmin。当k0选择不同的值时，对应的下垂系数在增大或减小时的裕度不同，即下垂特性曲线的摆动幅度不同，取

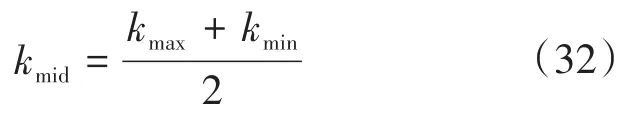
则当k0>kmid时，k0趋于kmin时的裕度较大，即当系统负荷突然减小或分布式电源出力突然增大时，其系统下垂特性曲线摆幅更大，因而惯性支撑能力更强；当k0>kmid时，k0趋于kmax时的裕度较大，即系统负荷突然增大或分布式电源出力突然减小时，惯性支撑能力更强。

3.4 飞轮系统控制系统变流器控制方案

飞轮系统整流器的控制方案与单轴结构的微型燃气轮机系统类似，在其基础上改进后的控制过程为：变流器的输出电压Udc经过求导运算得到直流母线电压变化率dU∕dt，根据式（31）求出实时下垂系数k，根据式（13）求得此时变流器的功率输出参考值，随后根据式（12）生成角速度的参考值，由PI控制生成内环电流参考值。其内环控制采用isd=0的矢量控制。飞轮系统控制框图如图5所示。

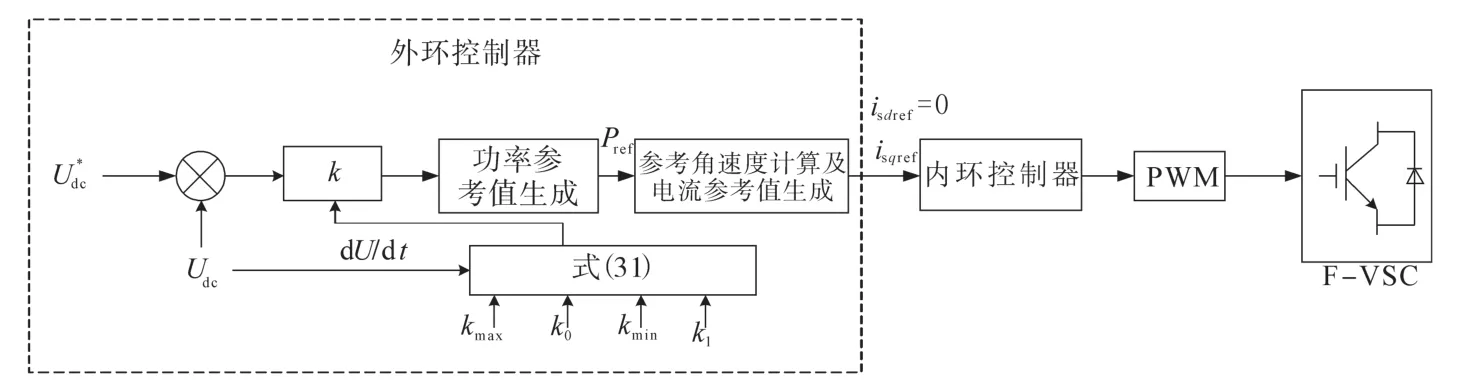
图5 飞轮系统控制框图Fig.5 Control block diagram of flywheel system

4 仿真分析

4.1 仿真系统简介

为验证本文提出的惯性策略的有效性，在Matlab∕Simulink仿真软件中搭建了仿真模型，飞轮系统控制策略见图5，但在实际控制中，电压变化率很难得到，因此本文使直流电压通过滤波器后用电压变化量δU代替电压变化率进行仿真。

仿真模型中，直流母线电压为760 V，取该值为基准值，仿真结果中变流器的功率以流向直流侧为正，电压为标幺值。

4.2 仿真验证

4.2.1 功率突增仿真

初始状态下，负荷功率约为15 kW，Udc被变流器控制在748 V即0.984（标幺值）。光伏系统输出功率约为9 kW，储能系统输出功率约为5 kW。1 s时，系统负荷突增为33 kW。仿真波形如图6所示。取系统电压变化最大值与系统稳定运行时电压的差值百分比作为电压的偏差率，取功率相对于稳态时的功率作为功率偏差率。仿真结果如表1所示。

表1 负荷突增仿真结果Tab.1 Simulation results of load surge

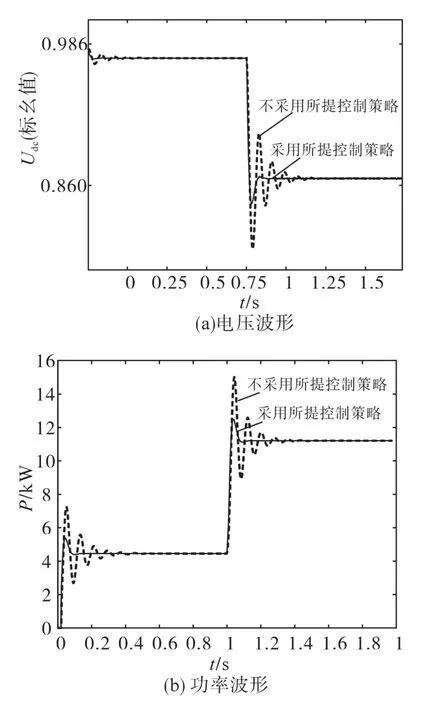
图6 负荷突增情况下的仿真波形Fig.6 Simulation waveforms under load surge

当系统功率突然增大时，不采用所提惯性控制策略，电压最大偏差量为26.5 V，其电压偏差率为3.543%。系统功率最终稳定至11.2 kW；当采用所提惯性控制策略且此时k1=100时，电压偏差量为20.5 V，偏差率为2.741%。功率最大偏差率为11.339%。即当采用所提惯性控制策略后，电压偏差最大值降低6 V，偏差率降低0.802%。功率偏差降低22.671%。即所提惯性控制策略可以有效提升系统功率变化时的稳定性。

对于所提惯性控制系统而言，改变系数k1可以改变系统的惯性支撑效果。运行工况相同，其仿真如图7所示。当k1=200时，系统电压最大降为729.5 V，其电压偏差率为2.473%。功率最大增至11.71 kW，偏差率为4.56%。即在一定范围内增大系数k1，亦即增大系统的虚拟惯性。

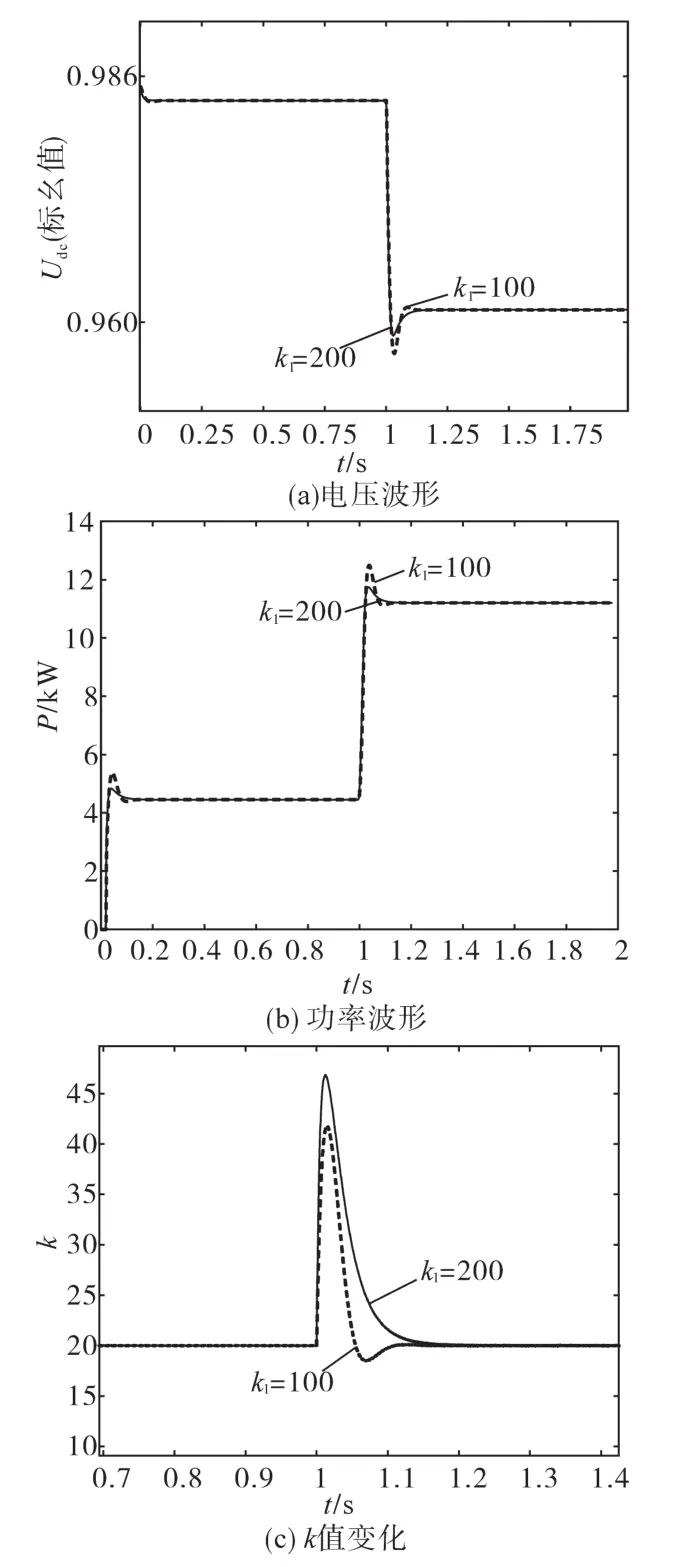
图7 改变k1时仿真波形Fig 7 Simulation waveforms when changing k1

4.2.2 光伏出力下降仿真

初始状态下，负荷功率约为20 kW。光伏系统输出功率约为12 kW，储能系统输出功率约为7.5 kW。1 s时，光伏出力突降为4 kW。仿真波形如图8所示。

如图8所示，当系统功率突然减小时，对比两种控制策略其电压偏差率由1.484%降低为1.337%，功率最大偏差量降低了0.577 kW。即所提惯性控制策略在系统出力减小时仍能够发挥控制效果。改变k1所得到的仿真波形如图9所示，其电压最大偏差量下降2.6 V，功率最大偏差下降0.587 kW。即在系统出力减小时，仍能通过改变k1提升系统的虚拟惯性。

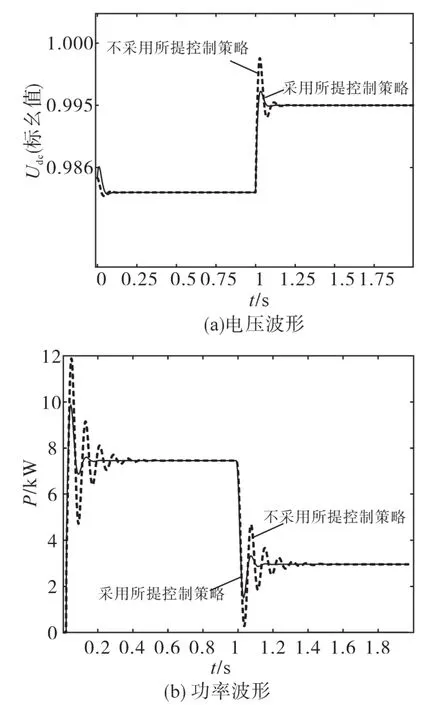
图8 光伏出力突降情况下的仿真波形Fig.8 Simulation waveforms under sudden drop of photovoltaic output

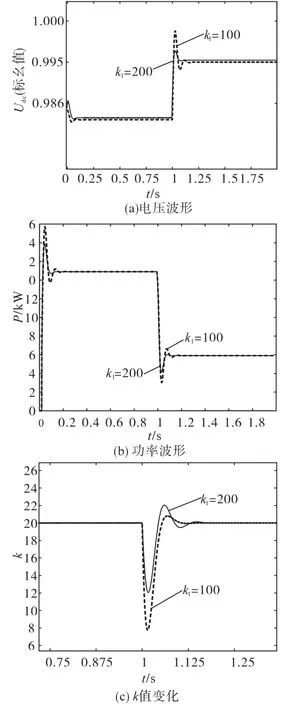
图9 改变k1时仿真波形Fig 9 Simulation waveforms when changing k1

5 结论

本文针对飞轮储能系统提出了一种基于变下垂系数的虚拟惯性控制方法，并构建了新的变下垂系数函数。理论与仿真结果表明：

1）用变下垂系数的虚拟控制方法取代固定的下垂系数，可以有效提高系统的虚拟惯性，减小系统的电压和功率波动。

2）所提的惯性控制策略可以通过初始斜率的改变，进一步发挥其惯性支撑效果。

3）所提控制策略应用在飞轮储能系统变流器上，可完善其对直流配电网的电压和功率调节能力，从而显著地提高了直流配电系统的供电质量。