一种输入并联输出串联模块化LCC谐振变换器

杨晓光 ，李宇麒 ，高正 ，席利根 ，温静

（1.省部共建电工装备可靠性与智能化国家重点实验室（河北工业大学），天津 300130；2.河北省电磁场与电器可靠性重点实验室（河北工业大学），天津 300130）

高压DC-DC变换器具有广泛的应用范围，如激光器、X射线电源、分析仪器与静电除尘等领域[1-4]。串并联谐振式（LCC）变换器拓扑由于其自身的软开关能力和升压特性，广泛应用于高压变换器中[5]。高压变换器一般由高频DC-AC逆变器、谐振腔、高压变压器和整流器组成，其中变压器是DC-DC变换器的关键部分，是实现更高电压等级和更高功率等级的瓶颈[6-7]。因此，为了降低单个变压器的电压应力，通常采用后级添加倍压电路（CW全波倍压电路、单极性半波倍压电路等）或多个子模块串并联的方法构成不同类型的高压DC-DC变换器，以满足高输出电压和高额定功率值的要求[8-10]。在这些类型的变换器中，输入并联输出串联（IPOS）模块化DC-DC变换器具有子模块组合灵活的特点，因而能够产生更高的功率或更高的输出电压。然而，各模块的器件参数难以达到完全一致，尤其是高压变压器的分布参数可能存在较大差异。模块间参数的差异可能会严重影响各模块之间的均压，因而限制了IP⁃OS DC-DC变换器的应用。为了保证变换器的可靠工作，必须确保各模块的输出电压均衡[11]。

目前解决模块间均压问题的方法一般是通过主动的控制措施，例如：文献[12]提出了一种最大电压均压法，即以最大的输出电压为参考调节各模块输出电压；文献[13]提出了一种主从控制策略和分布式电压控制器来实现输出功率的均衡，另外还有同时控制均压均流的双环控制法[14]等。这些控制策略，都需要在各模块上配置电压或电流检测装置，增加了电路的复杂性，降低了系统的整体可靠性[15]。针对这一问题，本文提出了一种具有自动均压输出特性的IPOS模块化LCC变换器，不需要添加外围控制电路和复杂的控制算法即可实现模块间自动均压。

1 变换器结构和工作原理

为了便于分析，本文以两模块为例给出所提出的IPOS变换器，其电路拓扑如图1所示。对比传统IPOS变换器[16-17]，新型拓扑是在传统拓扑的基础上，将两个模块的整流输出电路交错连接，以实现均压的目的。在模块1（图1 Module-1）中，Qi，1（i=1，2，3，4）为4个开关管；Di，1（i=1，2，3，4）为其寄生二极管；Ls，1，Cs，1，Cp，1，Tr1分别为串联电感、串联电容、并联电容和变压器；DRi，1（i=1，2，3，4）为整流电路的4个二极管；Co，1为输出滤波电容；变压器变比1：k1；Io，1为输出电流。模块2（图1的Module-2）中的各个参数定义相同。

图1 提出的IPOS变换器电路拓扑Fig.1 Topology of the proposed IPOS converter

本文以两模块串联电容Cs参数不一致（Cs，1＜Cs，2）为例，来分析参数差异对均压特性的影响。假设LCC变换器工作于第一种电感电流断续模式（discontinuous current mode 1，DCM1）[18]，则IP⁃OS变换器的主要波形如图2所示。由于1个周期内前半周期[t0≤t＜t4]与后半周期[t4≤t＜t8]的电路特性对称，因而只给出前半周期的等效电路（见图3～图9）和模态分析。

图2 在Cs参数差异情况下提出的变换器主要波形Fig.2 The key waveforms of the proposed converter when the modules having different values of Cs

1）模态 1[t0≤t＜t1]：模态 1 的等效电路图如图3所示。在t0时刻之前各模块的串联谐振电流ir，j（j=1，2）为零，所以t0时刻开关管Q1，j和Q4，j零电流开通。ir，j流经 Q1，j，Cs，j，Ls，j，Trj，Q4，j，此时，Ls，j和 Cs，j两元件谐振。整流二极管 DR1，j，DR4，j导通，并联谐振电容 Cp，j上电压 VCp，j被输出电压钳位在 Vo，j∕kj，两模块分别向各自的副边滤波电容传能。

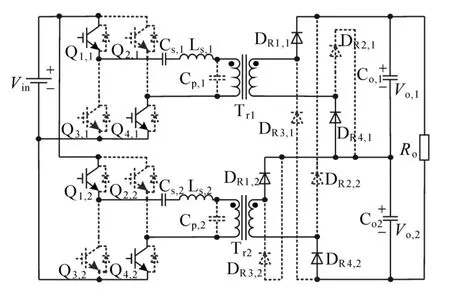
图3 模态1（t0—t1）Fig.3 Mode 1（t0—t1）

2）模态2[t1≤t＜t1']：模态2的等效电路图如图4 所示。由于 Cs，1＜Cs，2，模块 1 谐振电流 ir，1必先于模块2谐振至过零点（即t1时刻）。t1时刻之后，ir，1反向增大，流经 D4，1，Cp，1，Ls，1，Cs，1，D1，1，此时，Ls，1，Cs，1和 Cp，1三元件谐振。Cp，1通过 ir，1放电，VCp，1从 Vo，1∕k1下降。模块1的谐振能量流向电源侧，副边二极管均截止，Tr1原副边之间不再有能量传递，Co，1向负载供电。而模块2仍重复模态1的过程向 Co，2传能。

图4 模态2（t1—t1'）Fig.4 Mode 2（t1—t1'）

3）模态3[t1'≤t＜t2]：模态3的等效电路图如图5所示。在t1'时刻，模块2谐振电流ir，2正向谐振至零，之后反方向增加，流经 D4，2，Cp，2，Ls，2，Cs，2，D1，2，此时，Ls，2，Cs，2和 Cp，2三元件谐振。Cp，2通过ir，2放电，VCp，2从 Vo，2∕k2下降。模块 1 的谐振能量流向电源侧，副边二极管均截止，Tr2原副边之间不再有能量传递，Co，2向负载供电。而模块2仍然重复模态 2 的过程。此时，负载由 Co，1和 Co，2共同供电。

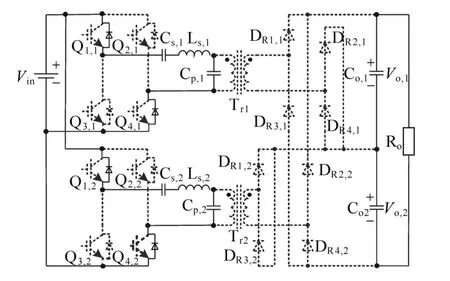
图5 模态3（t1'—t2）Fig.5 Mode 3（t1'—t2）

4）模态4[t2≤t＜t2']：模态4的等效电路图如图6所示。t2时刻，模块1的并联谐振电容Cp，1两端电压达到-Vo，2∕k1，整流二极管 DR2，1，DR3，1导通，此后 VCp，1被钳位至-Vo，2∕k1。谐振电流 ir，1流经 D4，1，Ls，1，Cs，1，Tr1，D1，1，此时，Ls，1和 Cs，1两元件谐振。模块1谐振网络的能量通过模块2的电容向负载侧传递能量，实现了两模块间能量的交换。模块2仍重复模态3的过程。

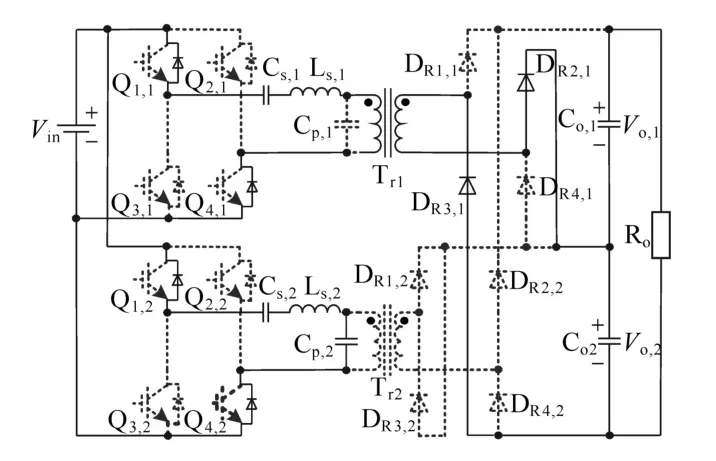
图6 模态4（t2—t2'）Fig.6 Mode 4（t2—t2'）

5）模态5[t2'≤t＜t3]：模态5的等效电路图如图7所示。t2'时刻，模块 2 的并联谐振电容 Cp，2两端电压也达到-Vo，1∕k2，整流二极管 DR2，2，DR3，2导通，此后 VCp，2被钳位至-Vo，1∕k2。此时，模块 2 谐振网络的能量通过模块1的电容向负载侧传递能量，也实现了两模块间能量的交换。模块1仍重复模态4的过程。这样，模块1向Tr2副边供电，模块2向Tr1副边供电，实现了能量的交换。

图7 模态5（t2'—t3）Fig.7 Mode 5（t2'—t3）

6）模态6[t3≤t＜t3']：模态6的等效电路图如图8所示。t3时刻，模块1的谐振电流ir，1谐振至零，由于 Q1，j和 Q4，j已经在 t1'—t3时间段内零电压关断，t3时刻之后，ir，1保持为零，Tr1原副边之间不再有能量传递，Co，1向负载供电。模块2仍重复模态5的过程。

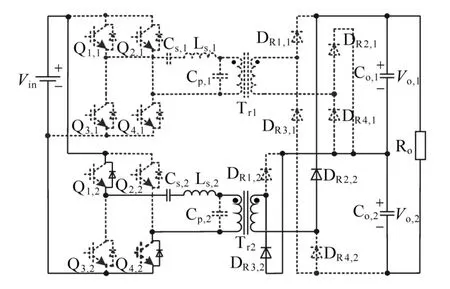
图8 模态6（t3—t3'）Fig.8 Mmode 6（t3—t3'）

7）模态7[t3'≤t＜t4]：模态7的等效电路图如图9 所示。t3'时刻，模块 2 的谐振电流 ir，2也谐振至零。同理，t3'时刻之后，ir，2保持为零，Tr2原副边之间不再有能量传递，Co，2向负载供电。模块1仍重复模态 6 的过程，此时，负载侧由 Co，1和 Co，2共同供电。

图9 模态7（t3'—t4）Fig.9 Mode 7（t3'—t4）

2 均压性能分析

由模态分析和图2的输出电流波形可知，一个周期内：模块1在t0—t1和t6—t7时间段内，向模块1的等效负载传能；而在t4—t5和t2—t3时间段内，向模块2的等效负载传能。反之，模块2在t4—t5'和t2'—t3'时间段内，向模块1的等效负载传能；而在t0—t1'和 t6'—t7'时间段内，向模块 2 的等效负载传能。可见，新型变换器的整流电路不同于传统IP⁃OS变换器桥式整流电路的传能方式，其利用两模块交替向自己和相邻的等效负载传能的特点，使得模块间的等效负载在模块间参数不一致时也能趋于均衡，从而能够实现输出均压。

为了进一步说明其均压特性，本文采用状态空间平均法[15]对所提出的变换器进行了分析。

令Tab（T01，T11'，T1'2，…，T7'8）表示各模态的时间间隔。1个周期内的各个工作模态中，IPOS变换器的电路状态都可以用一系列线性状态空间方程来表示。如图3～图9所示，该变换器1个周期内有14个工作模态，其相应的状态空间方程组为

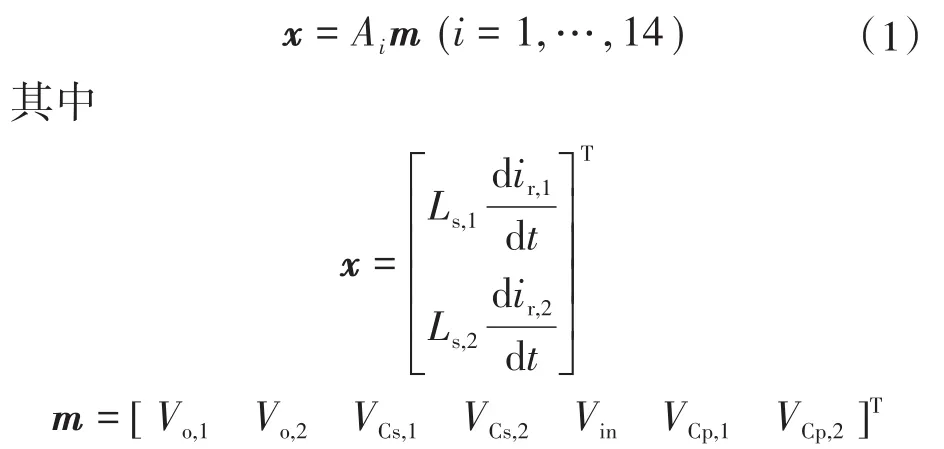
式中：m为输入独立电源与状态变量的线性组合而成的矩阵；A1～A14为各个工作模态的系统矩阵，与电路拓扑有关，可分别列出。

对状态空间方程组进行平均运算，即有==∙，可具体展开为

令Ts为1个开关周期，则可表示为

由于1个周期内状态变量的平均值等于零，即=0，==0，==0，将其代入式（2），可得：

由图2可知，各单模块LCC的模态转换时间（Tab）可由电路参数表示，其中T03=T47，T03'=T47'，T01=T45，T67=T23，T01'=T45'，T67'=T23'，将其代入式（4）中，即可解得=。这说明当两模块间参数不一致时，输出电压总能在稳态时达到均衡。

3 实验

本文试制了一台两模块样机，用于对比测试传统IPOS变换器与所提出变换器的性能。通过改变后级整流块的连接方式，其它方面都相同，即可实现两种变换器之间的切换。

变换器的基本参数为：输入电压Vin=25 V，输出功率 Po=400 W，各模块的谐振参数为 Ls，1=Ls，2=3 μH，Cs，1=Cs，2=5 μF，Cp，1=Cp，2=2.1 μF，变压器变比k1=k2=7.5，开关频率fs=20kHz。变换器无外围控制电路，驱动脉冲由型号为TMS320F28335的DSP产生。

对传统变换器与新型变换器在两模块间参数不一致情况下进行测试：1）Cs，1=5 μF，Cs，2=4 μF情形；2）k1=7.8，k2=7.2 情形；3）Cs，1=5 μF，k1=7.8；Cs，2=4 μF，k2=7.2 情形。图 10 为 Cs，1=5 μF，Cs，2=4 μF时两种变换器实验波形。

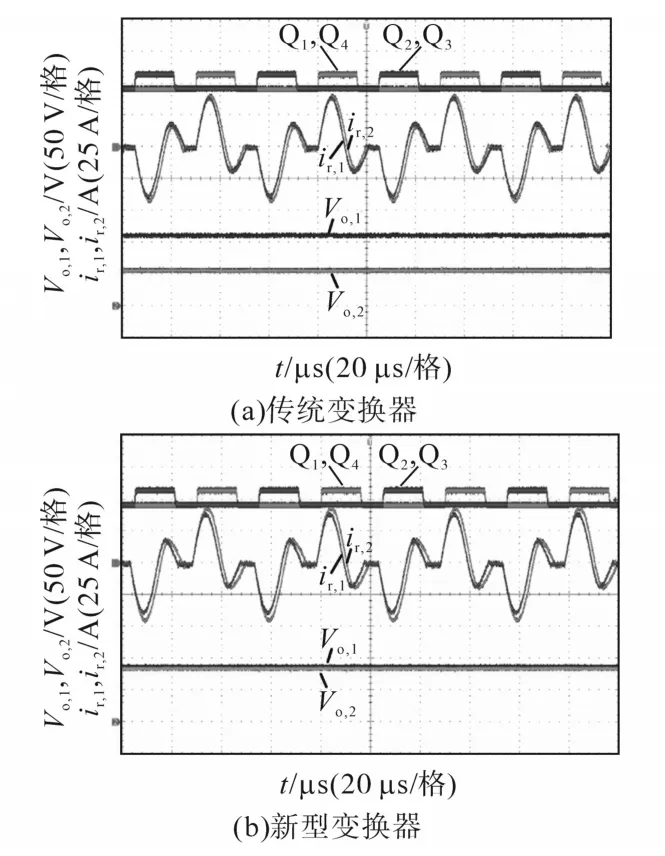
图10 Cs，1=5 μF，Cs，2=4 μF 时两种变换器实验波形Fig.10 Experimental waveforms of the two converters in the case of Cs，1=5 μF and Cs，2=4 μF

图11为当k1=7.8，k2=7.2时，两种变换器实验波形。

图11 k1=7.8，k2=7.2时两种变换器实验波形Fig.11 Experimental waveforms of the two converters in the case of k1=7.8 and k2=7.2

图 12为 Cs，1=5 μF，k1=7.8；Cs，2=4 μF，k2=7.2时两种变换器实验波形。

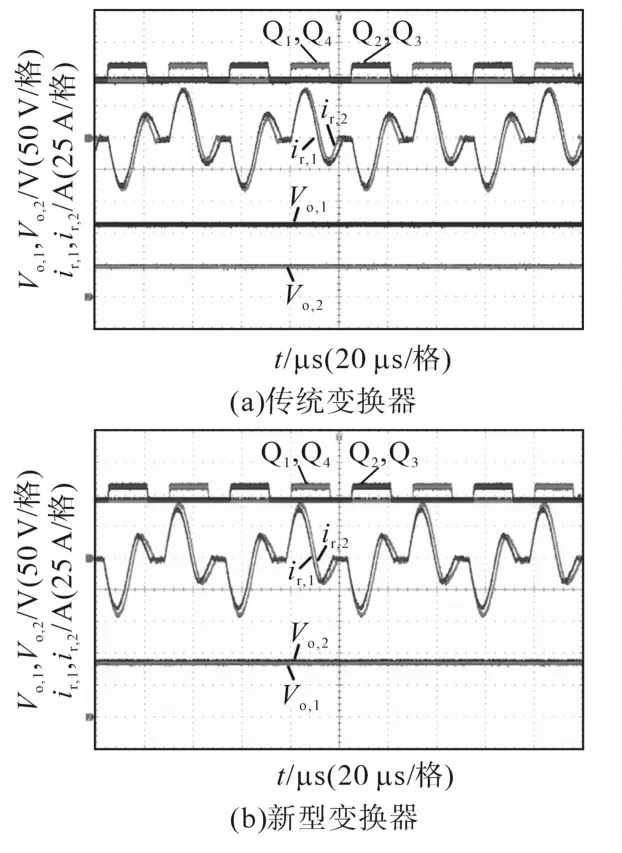
图12 Cs，1=5 μF，k1=7.8；Cs，2=4 μF，k2=7.2时两种变换器实验波形Fig.12 Experimental waveforms of the two converters in the case of Cs，1=5 μF，k1=7.8 and Cs，2=4 μF，k2=7.2

由图10～图12可知，模块间的参数差异无论是对传统变换器还是新型变换器中的谐振电流影响不大。然而，传统变换器中子模块的输出电压受参数差异影响较大，模块间电压不均衡现象严重，相比之下，新型变换器则拥有良好的输出均压特性。

图10～图12中的子模块输出电压值如表1所示。

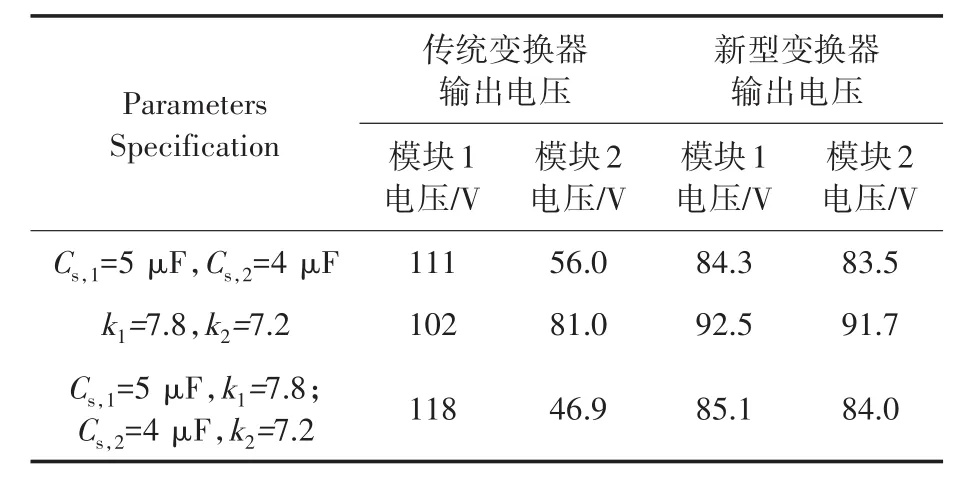
表1 传统变换器与新型变换器的模块输出电压Tab.1 Output voltage of module converters for conventional converter and proposed converter

图13为所提出的变换器在图12参数配置下受输入电压Vin或负载Ro的阶跃扰动时两模块输出电压的暂态波形，其中，图13a为Vin从25 V突变至19 V时，输出电压的暂态波形；图13b为Ro从60 Ω跳变至100 Ω时，输出电压的暂态波形，tr时刻表示发生阶跃扰动，tp时刻表示输出电压达到最大超调量，ts时刻表示输出电压达到稳态。

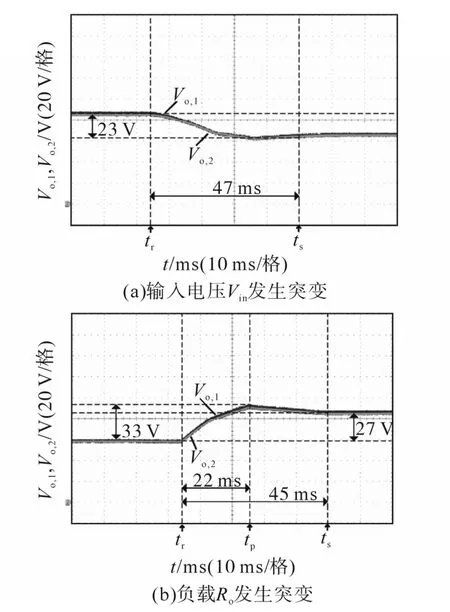
图13 新型变换器的暂态特性Fig.13 Transient response of the proposed converter

由图13可知，图13a在Vin突变下的暂态调节时间为47 ms，输出电压波动为23 V，并无超调；图13b在Ro突变下的暂态调节时间为45 ms，输出电压波动27 V，最大超调量6 V，峰值时间22 ms。由图13可以看出，新型变换器在多种参数差异下，受到输入电压Vin的阶跃突变或是负载电阻Ro的阶跃突变时，都可以达到稳态，这说明所提出的变换器整体是稳定的。并且，在暂态过程（tr—ts）中仍没有出现输出电压失衡的现象，而文献[12-14]虽然通过控制策略也能在较短的调节时间内达到模块间均压，但在动态调节过程中不能保持模块间电压的均衡。

4 结论

本文提出了一种具有自动均压输出特性的IPOS模块化LCC DC-DC变换器，即使模块间存在较大的参数差异，该变换器也能在输入电压突变或负载突变的情况下实现均压。该变换器有效地克服了传统变换器额外控制措施所带来的电路复杂性，提高了电路稳定性和可靠性。该变换器的特点使之可应用于高压电源。