基于准Z源有源功率解耦的改进调制策略
(四川大学电气工程学院,四川 成都 610065)
近年来,分布式发电系统发展迅速。与传统集中式发电系统相比,有距离用户更近,发电灵活性更高等特点[1]。而单相逆变器可靠性高,配置灵活,成本较低,使其非常适合于应用在分布式发电系统中。但如何提高单相逆变器的运行效率、改进并网控制策略、减小体积,是单相逆变器分布式光伏发电系统迫切需要解决的问题。
准Z源变流器(quasi-Z-source inverter,qZSI)具有诸多优点:可在单级变换结构中同时实现DC-DC和DC-AC变换;无需加入死区时间故不会造成输出波形畸变,可靠性高。基于上述优点,准Z源逆变器被应用于新能源发电系统、交流调速、电动汽车中。但准Z源网络拓扑存在一些缺陷,例如所需电容电感过大,这造成了准Z源体积大,成本高的问题[2],这些问题在单相系统中尤为突出,因为直流侧和交流侧的瞬时功率不相等,变流器的直流侧总会出现二倍工频(2ω)功率脉动,使直流链电压不稳定。该脉动不仅使准Z源网络中电流、电压瞬时值增大,还可能导致一些磁性元件饱和,在光伏应用中会带来MPPT效率下降等问题[2],所以为了抑制2ω脉动,传统准Z源网络参数通常取得较大[3],这将进一步导致准Z源体积过大,功率密度下降,限制了其在工业界的应用。因此抑制2ω脉动,减小单相准Z源体积与成本,提高其运行效率就颇为重要。
近年来,为了抑制2ω功率脉动,国内外学者进行了大量研究,提出了多种新型解决方案,其中有源功率解耦(active power decoupling,APD)方法因其效率高,功率密度高而得到广泛应用[4-7]。而APD方法按照储能元件类型可将解耦拓扑分为电感储能型[4]和电容储能型[5-7]。由于前者通常具有较高的铁心损耗和绕组损耗,因而从效率的角度来看,基于电容储能的APD拓扑更具竞争力。其解耦拓扑根据电容和电感连接位置可分为 Buck型、Boost型和 Buck-Boost型等拓扑[8]。Buck型解耦拓扑有着开关管电压应力小的优势,但由于解耦电容电压波动较小,其功率解耦能力有限,在实际应用中需要较大的电容才能完成功率解耦。Buck-Boost型拓扑中解耦电路开关管的电压应力是解耦电容电压和直流链电压之和[9],这使得解耦电路开关器件承受的电压应力过大。相比而言,Boost型APD拓扑具有解耦电容小、电压应力适中、功率解耦能力强等特点,结合单相准Z源的特性,提出将Boost型APD解耦电路应用在单相准Z源上,构成Boost型APD-qZSI(active power decoupling qZSI)的拓扑结构。与传统单相APD电路不同,Boost型APD-qZSI由于直流链电压断续[3],工作状态较之传统单相电路更复杂。本文基于状态空间平均法分析了Boost型APD-qZSI的四种工作状态,结合电容值和开关管电压应力、输出功率的关系给出解耦电路电容的取值方法。并具体分析解耦电感波动和调制方式的关系,提出了使解耦电感波动最小的调制方法。根据并网要求,本文采用了结合升压控制、并网电流控制和APD电路控制的控制策略。
1 传统单相准Z源并网逆变器
传统单相qZSI拓扑如图1所示,输入侧直流电压经过qZSI阻抗网络,通过一个单相H全桥进行逆变,再经过滤波器并入电网。
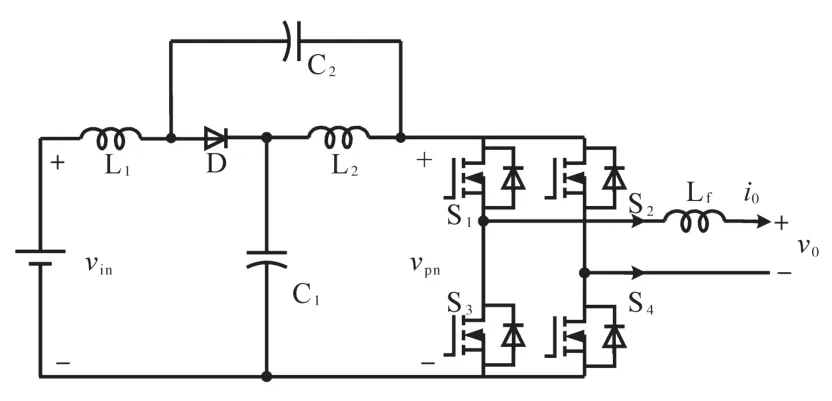
图1 传统单相准Z源逆变拓扑Fig.1 Traditional single phase qZSI topology
qZSI的工作原则如文献[2]所示,其通过同侧桥臂S1,S3(或S2,S4)同时导通进行升压,称为直通状态;当异侧桥臂S1,S4(或S2,S3)导通时,工作状态和传统H桥逆变器相同,称为非直通状态。稳态运行时,非直通状态下直流链电压峰值vpn_peak与直流输入电压vin的关系为
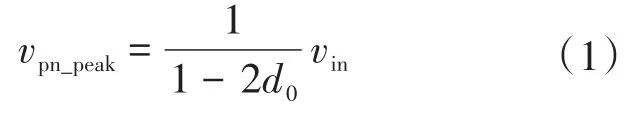
式中:d0为qZSI直通状态占空比;vin为输入直流电压。
小功率逆变器在并网时不需要提供无功功率,电流i0通常以单位功率因数并网,设网侧电压、电流为v0,i0,V0,I0为其峰值:
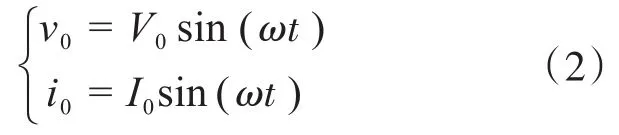
可以得到交流侧功率Pac表达式:
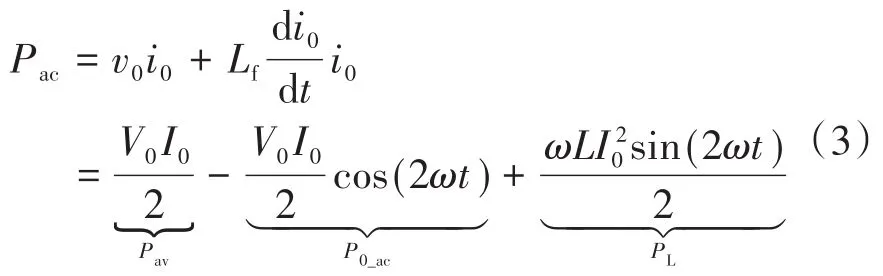
式中:Lf为滤波电感;Pav为平均功率;P0_ac为不考虑滤波电感功率脉动的交流侧纹波功率;PL为滤波电感的脉动功率。
如式(3)所示,瞬时功率由 Pav,P0_ac,PL三部分组成。其中P0_ac和PL的脉动频率是工频的两倍,两者之和定义为P2ω。为满足瞬时功率守恒,P2ω将在qZSI网络及直流输入电压侧中引起频率为工频两倍的电压及电流脉动,在本文称为2ω脉动。
通过对传统准Z源的阻抗网络L1,L2,C1,C2进行合理取值可以支撑脉动功率,并将直流母线电压脉动限制到工程允许的范围内。文献[3]给出了抑制2ω脉动的准Z源阻抗网络设计原则公式:
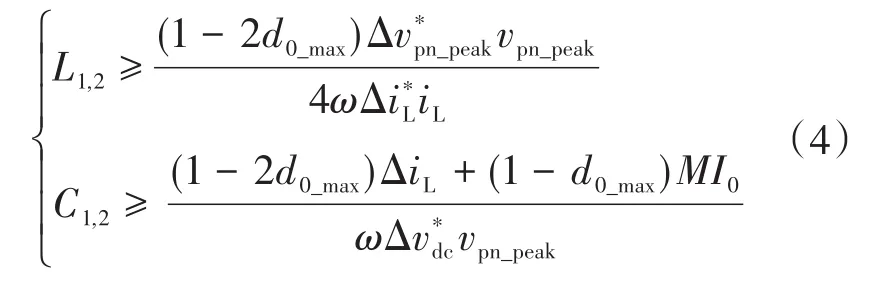
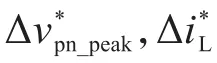
2 Boost型APD-qZSI电路原理
2.1 解耦电路纹波功率吸收原理
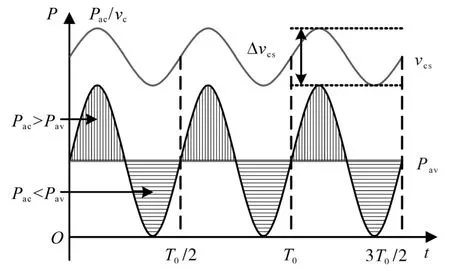
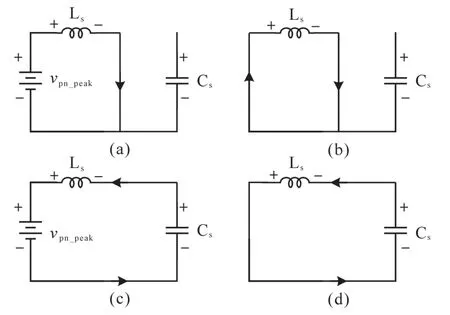
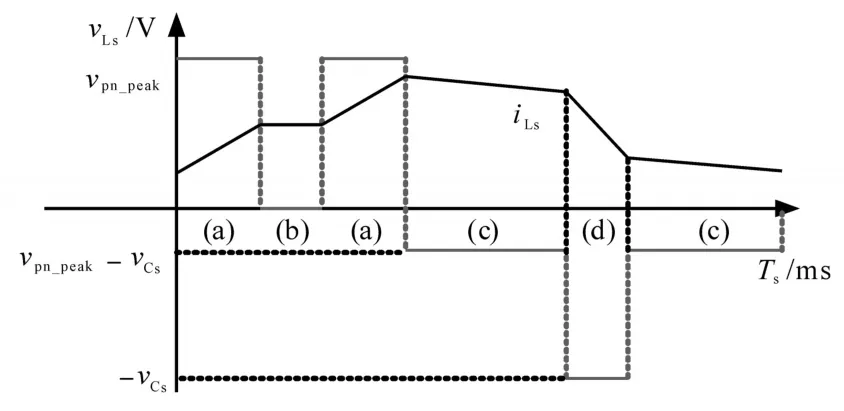
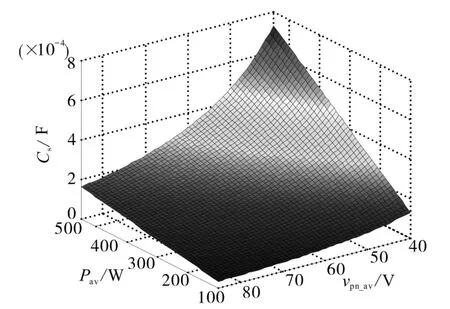
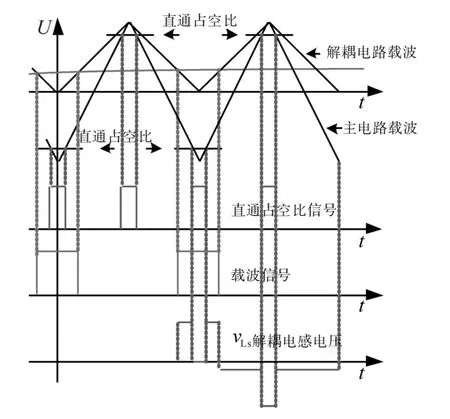
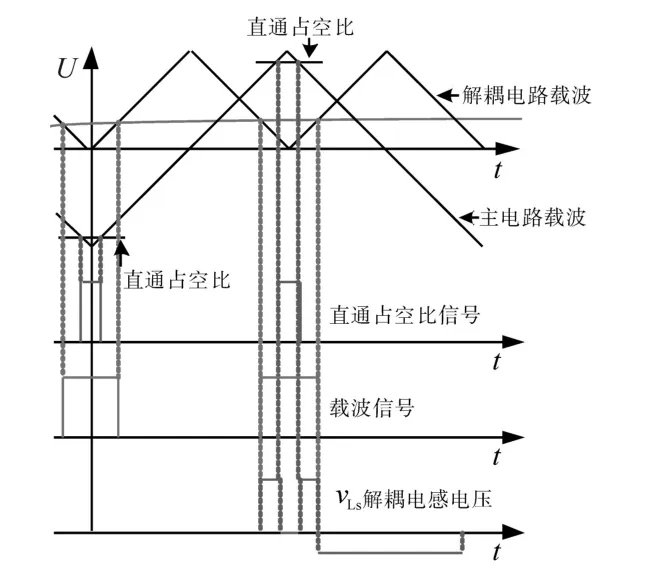
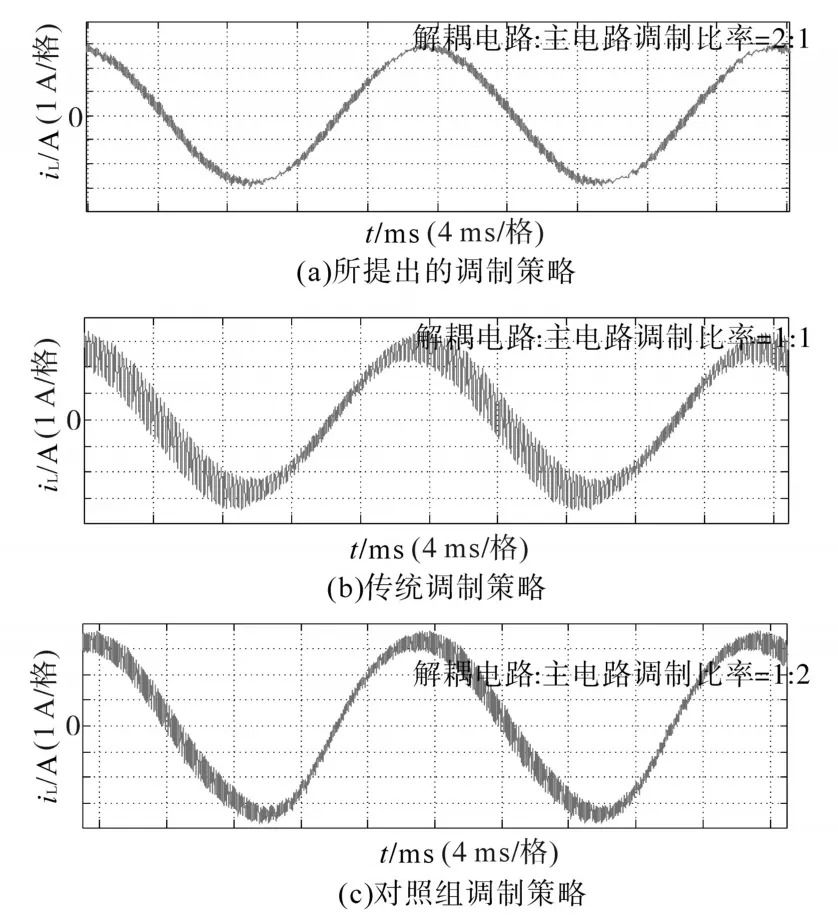
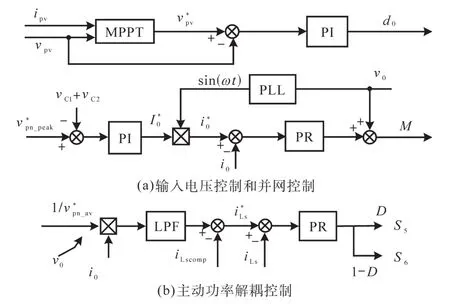
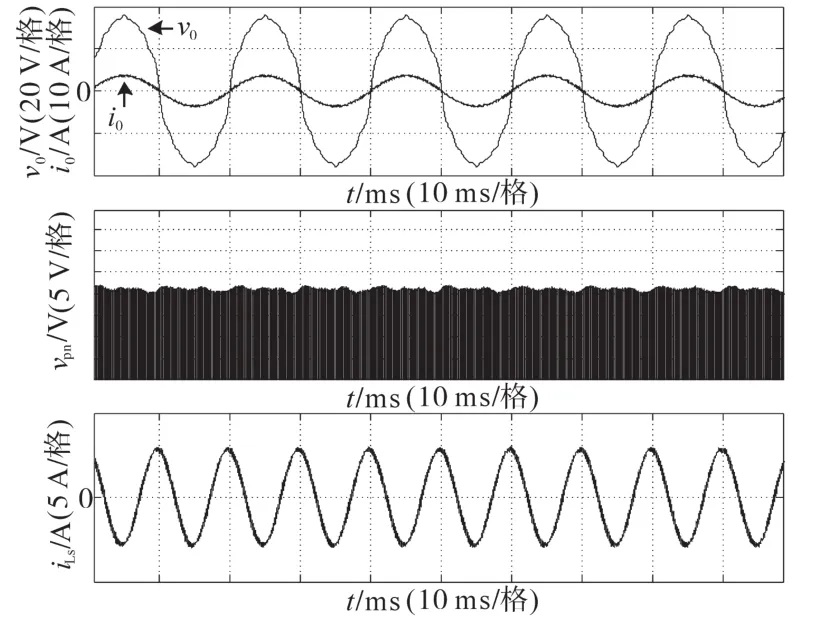
图2为Boost型APD-qZSI的拓扑结构,与传统qZSI相比,该拓扑增加了以直流链为输入、解耦电容Cs为输出的双向Boost型解耦支路。解耦电容电压vCs和交流侧功率Pac的关系如图3所示,当瞬时交流功率Pac>Pav时,解耦电容器充电,电容电压上升,以储存交流侧多余的纹波功率;当Pac 图2 Boost型APD-qZSI逆变拓扑Fig.2 Boost type APD-qZSI topology 图3 交流侧功率与解耦电容电压关系Fig.3 Relationship between AC side power and decoupling capacitor voltage 设解耦电路电容完全储存2ω脉动功率,可以得到解耦电容储存的能量为 式中:Cs为解耦电容的容值;vCsmax,vCsmin分别为解耦电容电压的最大值和最小值。解耦电容的能量用来储存P2ω,因此解耦电容容值应该按P2ω达到最大功率时确定,结合式(3)、式(5),有: 将式(3)中P2ω表达式代入式(6),可得: Boost型APD-qZSI解耦电路工作原理与传统单相解耦电路不同。传统单相解耦电路的vCs和直流链电压呈简单的Boost电路升压关系,但由于准Z源通过直通状态升压,解耦电路的直流链电压vpn是断续的,即直通状态时vpn=0 V;非直通状态时vpn=vpn_peak,所以需要重新确定vCs和直流链电压的关系,以确定解耦电路元件的参数取值。结合上述解耦电容的充、放电两种状态,Boost型APD-qZSI解耦电路一共有四种工作状态,如图4所示。 图4 解耦电路的四种工作状态Fig.4 Four operating states of Boost type APD-qZSI 由电感伏秒平衡列写方程,得到四种工作状态解耦电感的电压。由图4a得:vLs=vpn_peak;由图4b得:vLs=0 V;由图4c得:vLs=vpn_peak-vCs由图4d得:vLs=-vCs;其中vLs为电感的电压,vCs为解耦电容电压,如表1所示。 表1 四种工作状态下的解耦电感电压Tab.1 vLsin four operating states 表1中(a),(b),(c),(d)分别为上述的四种工作状态。由于开关频率相对二倍工频较高,一个开关频率周期内可近似认为vCs,iLs不变。以vCs升压时为例,由于qZSI直通状态的加入,一个开关频率内解耦电感电压vLs及其电流iLs如图5所示。 图5 解耦电感电压及电流Fig.5 Decoupling inductor voltage vLsand its current 图5中Ts为解耦电路高频开关周期。分别设Di(i=1,2,3,4)为四种工作状态在一个Ts内的占空比,可以得到下式的换算关系: 式中:D为解耦电路占空比;d0为主电路占空比。 根据式(8),一个Ts内有: 将式(9)中的Di消除,得到vCs、解耦电路占空比D和准Z源主电路占空比d0间的关系: 设Dmod为解耦电路电容vCs相对于直流链电压峰值vpn_peak的变比,可以用准Z源主电路占空比d0和解耦电路占空比D来表示,其中D和d0在[0,1]内取值,可以得到Dmod取值范围,如下式所示: 由式(11)中D等于0可推得解耦电容电压的最小值vCsmin。Boost型APD电路中,vCsmin恰好等于直流链电压的平均值[9],设其值为vpn_av。如下所示: 设Dmod为解耦电路电容电压vCs相对于直流链电压峰值vpn_peak的变比,可以用准Z源主电路占空比d0和解耦电路占空比D来表示,其中D和d0在[0,1]内取值,可以得到 Dmod取值范围,如式(12)所示。式(13)由式(11)中D=0推得,可得解耦电容电压的最小值vCsmin。Boost型APD电路中,vCsmin恰好等于直流链电压的平均值[9],设此平均值为vpn_av。 为了使解耦电路元件参数设计更合理,应该从解耦电路在不同功率下主电路开关管的电流应力、电容的取值、解耦电路开关管电压应力这几个角度来考虑[9]。因为Boost型解耦电路调制、控制策略均完全独立于主电路[6],解耦电路对主电路中功率器件的电流应力没有影响。Boost型APD-qZSI应从后两个角度选取电容元件。 从经济性角度来说,我们希望选取容值小,耐压等级低的电容,然而根据式(7),我们必须在两者间做出平衡,而且,很多因素限制了电容电压不能过大:首先,开关管电压应力与vCsmax相等,其取值过大会导致开关管电压应力增加;其次,vCsmax过大将导致解耦电容电压波动过分剧烈,进而造成vCs波形含有较高比例的除2ω脉动外的其它谐波分量[7],这使得2ω脉动抑制效果变差;最后,vCsmax过大将会使开关管电流应力增加[9]。综上所述,取vCsmax=2·vCsmin。 图6为在不同功率应用下,Boost型APD-qZSI解耦电容和直流链电压大小的关系,可以看出在低功率不同电压等级的场合下,解耦电容的理论取值都非常小,Cs在10-5~10-4F等级,实际生产中可使用小体积的薄膜电容器实现。 图6 不同功率、直流链电压下的Cs取值Fig.6 Csvalue under different power & DC link voltage 解耦电感仅起到能量传输的作用,其电流作为解耦电路的一个控制量,波动不能太大,故电感有最小取值。需要注意,由于Boost型APD-qZ⁃SI有独特的工作状态,不同调制策略会引起电感波动的不同,本文调整了主电路和解耦电路的调制方式,使解耦电感脉动降低,并给出Boost型APD-qZSI中解耦电感最小理论取值方法。 电流脉动由一个Ts内电感两端的电压波动决定,由电感电压的状态空间平均方程,可得电感电压波动值Δi'L表达式: 式中:iLi,vi,Di为四种工作情况下解耦电感电流、端电压和占空比。 可以看到电感波动因四个电压电平交替作用产生,其中(b)工作状态下无电感电压波动,如图5所示。以升压为例,在一个周期内如果绝对值最高的正负两个电平v1,v4作用时间相对较长时,vLs的剧烈变化将会导致电感电流iLs剧烈变化,如图5所示,此时直通信号和载波信号如图7所示。当采用传统主电路和解耦电路开关频率相等的调制策略时,由于直通信号每个Ts内有两次植入,直通信号将有一半的时间单独作用,即电路工作在(d)状态下,满足vLs=-vCs,根据式(13),-vCs的绝对值在四种工作情况下最高,将会造成较大的电流波动。 图7 相同载波频率下的直通信号和载波信号Fig.7 Through signals and carrier signals at the same switching frequency 针对这个问题,本文提出一种改进的调制策略:将解耦电路载波频率设置为主电路的两倍。如图8所示,可以观察到,直通状态总会和升压状态重合,直通信号不再单独出现,这将意味着解耦电路不会工作在(d)工作状态,即vLs≠-vCs,电感电压波动显著降低。同时为了消除两倍开关频率的影响,加入一组对照:将主电路载波频率设置为解耦电路的两倍,此时直通信号仍有一半的时间单独作用,(d)工作状态仍会出现,其产生原理与图7所示的传统调制策略相同。图9为这三种调制策略解耦电感电流iLs波动的对比。可以观察到对照组调制策略的波动仍较大。 图8 解耦电路和主电路载波频率按2∶1比率调制下的直通信号和载波信号Fig.8 Decoupling circuit and main circuit carrier frequency modulated by 2∶1 ratio of the through signals and carrier signals 图9 改进调制比率前后的解耦电感电流iLs波动对比Fig.9 Comparison of decoupling inductor current iLsfluctuation before and after improving the modulation ratio 考虑解耦电路(d)的工作状态不再出现,最大电感电流波动表达式修正如下: 此时工作状态变为3个,Di与D,d0的关系为 由式(17)可得到解耦电感的最大波动电流ΔiLs。 式(16)消去vi,Di,得: 式中:εiLs%为允许波动的百分比,因解耦电路电流不要求具有较小的THD值,仅需满足控制足够稳定,εiLs%取值可以适当宽松,在本文中|εiLs|%取20%。 由式(18)可以得到电感的理论最小取值。 Boost型APD-qZSI解耦利用并联的解耦电路实现了2ω脉动功率的主动解耦,直流侧仅含少量的脉动电压、电流。因此准Z源网络仅需限制少量的低频纹波和高频纹波电压、电流,理论上来说,其取值可以大幅减小。文献[10]给出了不考虑2ω脉动时的参数取值方法,具体为 式中:Δv,Δi为电感电流及电容电压的纹波。 图10 Boost型APD-qZSI主控制图Fig.10 Master control diagram of Boost type APD-qZSI 式(20)的(a)部分为iLs*的主体部分,根据式(3),其值等于v0·i0的交流部分,因为Pav不易实时测量,这里用一个带通滤波器来滤除v0·i0的直流部分,公式如下所示: 式中:GBPF为带通滤波器;ζ为阻尼系数,ζ=0.33;h为谐波倍数,对于2ω脉动有h=2;ω为工频角频率。 式(20)的(b)部分为并网滤波电感Lf对解耦电路功率影响,在小功率的情况下,I0相对于Pav已经足够大,需考虑电感Lf的影响,所以在控制图中加入一个补偿环节iLscomp: 为了验证前述理论的正确性,用Matlab∕Simulink对Boost型APD-qZSI进行仿真,电网侧电源加入3,5,7,9,11,13,21等各次谐波。解耦电路电容Cs理论值由式(9)计算得157 μF,解耦电感Ls理论值由式(18)得1.13 mH。电网其余参数均根据前面章节参数选取法则选取,考虑到实际应用中电子器件的波动,我们将参数设置得适当宽松,参数如下:直流侧输入电压vin=30 V,输出电压峰值v0=37.5 V,直流链电压峰值vpn_peak=60 V,主电路开关频率fzs=10 kHz,解耦电路开关频率fs=20 kHz,滤波电感Lf=3 mH,准Z源电容C1=C2=400 μF,准Z源电感L1=L2=0.5 mH,解耦电路电容Cs=200 μF,解耦电路电感Ls=1.5 mH,解耦电容电压波动vCs=45~90 V。传统qZSI逆变器和Boost型APD-qZSI参数取值和仿真效果比较如表2所示。 表2 元件参数取值与波动Tab.2 Inverter simulation parameters of Boost type APD-qZSI 表2中ε%表示波动量占总量的百分比,可以观察到,传统qZSI阻抗网络元件取值较大,在本文的应用中阻抗网络的电感、电容均达到了mH级、mF级,最重要的是其无法从根本上抑制直流链电压的波动,导致直流链电压的波动量百分比ε'vpn%始终很高。在加入主动功率解耦电路后,准Z源网络的元件参数取值大大减小,达到百μH级、百μF级;并且由于解耦电路吸收了2ω脉动功率,阻抗网络的直流链电压vpn的脉动大幅减小,Boost型APD-qZSI仿真结果如图11所示。 图11 表2取值下Boost型APD-qZSI仿真波形Fig.11 Simulation waveform of Boost type APD-qZSI in table 2 本文针对传统单相qZSI网络电容电感取值大,且无法有效抑制工频2ω纹波的问题,对Boost型APD-qZSI进行了数学建模、解耦原理分析、参数取值方法分析、控制策略分析。结论如下:1)提出的Boost型APD-qZSI相对与传统qZSI大幅降低了电感电容的大小,有效地抑制了工频2ω纹波;2)所提出的改进调制策略减小了解耦电路电感波动,使得解耦电感有了更小的取值,进一步提高了逆变器功率密度;3)设计的针对Boost型APD-qZSI的控制策略可以很好地完成控制目标,且逆变器输出波形接近正弦波,电流波形THD值在5%以下。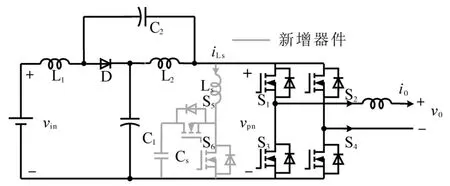
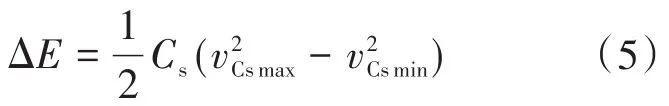
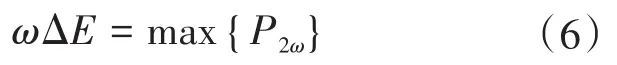
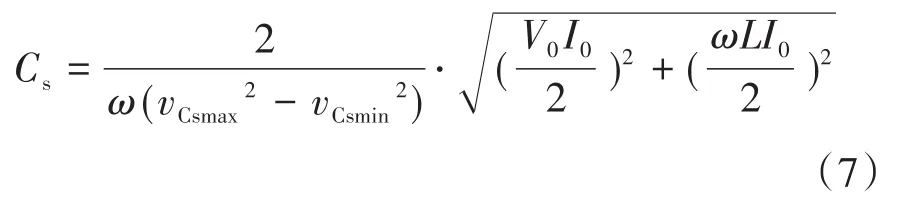
2.2 Boost型APD-qZSI解耦电路工作原理和vCs计算方法
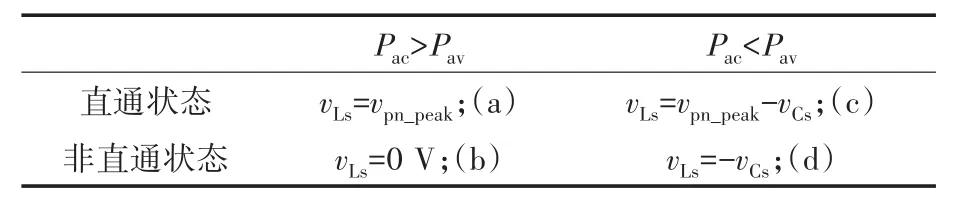
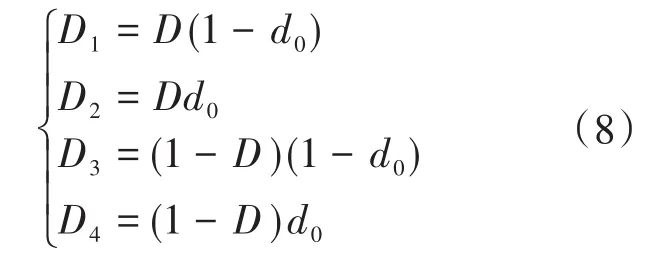
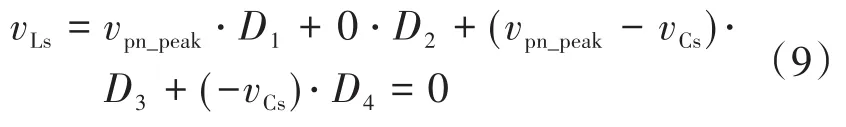
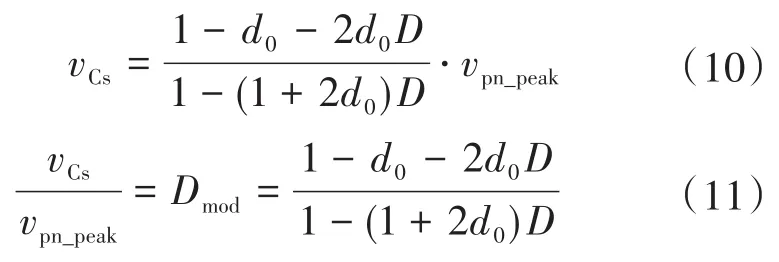
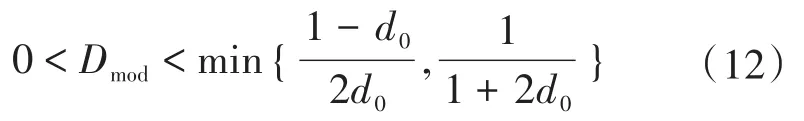
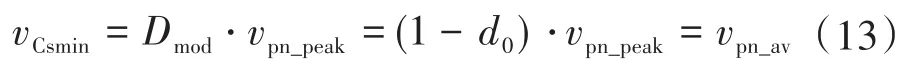
3 Boost型APD-qZSI参数取值
3.1 解耦电容取值
3.2 调制策略和解耦电感取值
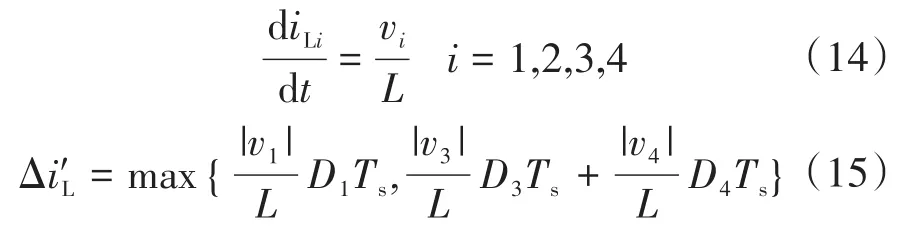
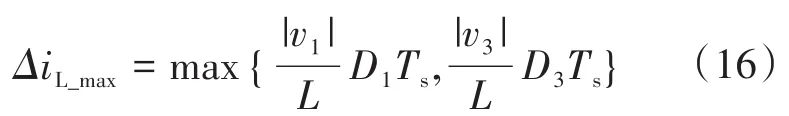

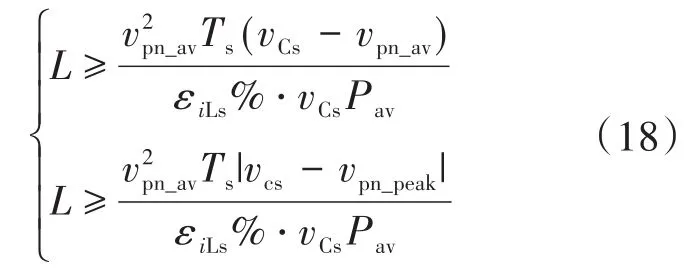
3.3 准Z源网络取值
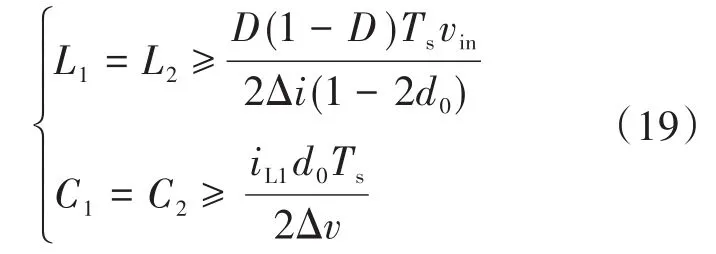
4 控制策略
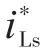
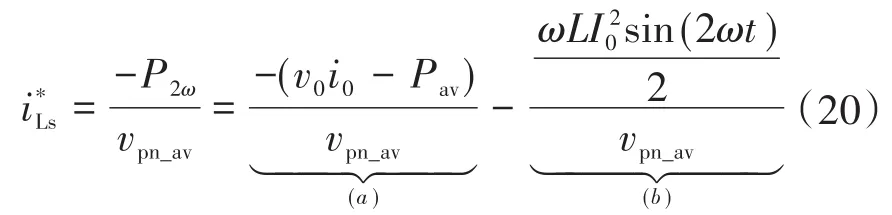
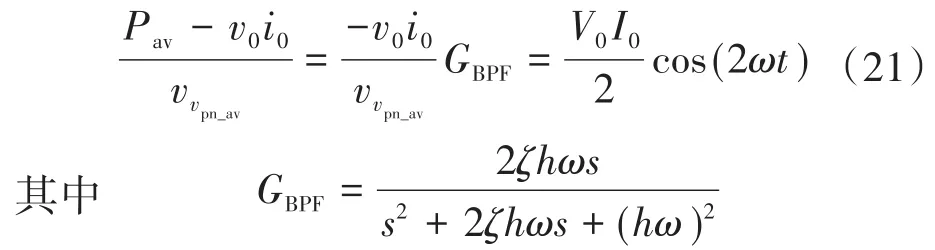
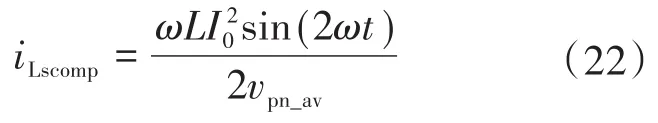
5 仿真验证

6 结论

