基于NOMA的上行MTC无线资源分配方案

马 莉，王茜竹，吴广富，王 超

(1.“新一代信息网络与终端”重庆市协同创新中心，重庆 400065；2.重庆邮电大学 电子信息与网络工程研究院，重庆 400065)

0 引 言

机器类通信(machine type communication，MTC)场景[1]包含两类不同服务质量(quality of service，QoS)要求的设备：高可靠低时延通信(ultra-reliable low latency communications，URLLC)设备和大规模机器类通信(massive machine type communication，mMTC)设备[2]。为了满足大量MTC设备的同时接入需求，引入了非正交多址接入(non-orthogonal multiple access，NOMA)技术。然而，MTC场景中不同QoS要求设备的混合接入给无线资源分配带来了严峻的挑战[3]。

目前，NOMA技术在MTC场景中的资源分配研究目标多为最大化能量效率[4,5]、最大化接入量[6,7]、最大化吞吐量[8,9]等。此外，S.Han等[10]提出了一种基于上行NOMA的联合功率和子载波的资源分配算法，提高了mMTC网络的保密容量；F.Fang等[11]研究了MTC设备在下行NOMA网络中的功率分配和集群调度方案，能较好降低设备功率；谷静等[12]以系统能效作为优化目标，利用自适应遗传算法(adaptive genetic algorithm，AGA)优化功率，改进了AGA的交叉和变异概率以避免较优解丢失，但作者直接以目标函数当成适应度函数，容易陷入局部最优解中。

针对上述问题，本文设计了一种基于NOMA技术的上行MTC资源分配方案。具体贡献有:①考虑了不同通信需求的MTC设备混合接入的情况，在满足URLLC设备QoS的前提下，建立mMTC设备功率优化模型；②设计了一种基于AGA的资源分配算法，并改进了混合变量的染色体编码规则，减少了变量个数，降低了约束矩阵维度，达到加快算法收敛速度的目的；③考虑了带约束的优化模型中种群可行解比例和单个个体满足约束的数量，对自适应惩罚函数进行应用和改进，提高算法搜索能力，并且保留种群次优个体以避免丢失较优解。

1 模型建立

1.1 MTC系统模型

1.2 URLLC设备QoS分析

URLLC设备拥有高速率低时延的通信特征，而相对地，mMTC设备低速率时延不敏感。当同一子载波上叠加有以上两类设备的时候，URLLC设备应具有更高的通信优先级，且允许至多一个URLLC设备和多个mMTC设备叠加在单个子载波。所以让URLLC设备以最大功率进行发送，保证较高的传输速率，将mMTC设备的接收功率暂时视作干扰。根据香农公式可以表示为

(1)

其中，pu,max为URLLC设备的最大发送功率，hu,n表示在子载波n上URLLC设备的信道增益，Ru,min表示URLLC设备应满足的最低传输速率，Bn表示单个子载波带宽，Iu,n表示URLLC设备受到的来自同一子载波n内其它mMTC设备的干扰，z表示子载波n上的噪声。

当URLLC设备以最大发送功率pu,max、以要求的最低传输速率Ru,min发送时，该设备在当前子载波n内所能忍受的干扰为

(2)

其中，In,max为由式(1)解得的URLLC设备所能忍受的最大干扰值。由式(2)可知，当URLLC设备的最低速率与发送功率均已知时，In,max取决于URLLC设备的子载波分配情况。

假设Y为U×N的0-1矩阵，矩阵元素yu,n为1表示URLLC设备u确认分配在对应子载波n上，反之矩阵元素yu,n为0表示该设备u不应分配在对应子载波n上。假设一个传输时间间隔(transmission time interval，TTI)中，每个URLLC设备最多被分配一个资源块(physical resource block，PRB)[6]，式(1)和式(2)可以重写为

(3)

1.3 mMTC设备功率优化模型

为了降低mMTC设备通信时收到的干扰，需要从原信号中使用SIC技术将解调出的URLLC信号消除，再对mMTC设备进行解调。接收端解调时，会按照接收功率由大到小的顺序对相应设备进行操作。同一子载波内未解调设备会干扰正在解调的设备。将同一子载波内的mMTC设备信道增益以降序的形式排列，设备mk在子载波n上受到的干扰Ik,n可以表示为

(4)

(5)

其中，pk,n为mk的发送功率，hk,n为mk在子载波n上的信道增益。

假设P为M×N的矩阵，矩阵中的元素pk,n为取值连续的功率变量；X为M×N的0-1矩阵，矩阵元素xk,n为1表示mMTC设备是分配在对应子载波的标识变量，反之，为0表示未分配。假设每个mMTC设备最多可以在一个TTI中分配一个PRB[6]，则式(4)、式(5)可以重写为

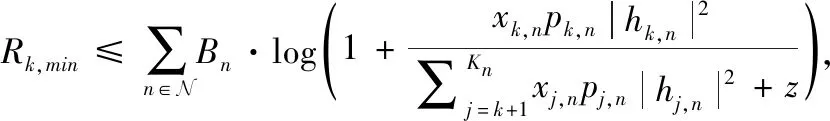
(6)

为了保证SIC接收机正确接收，当前待解调的mMTC设备功率应大于相同子载波内其它设备对其产生干扰的功率之和[8]。结合子载波分配标识xk,n，该条件可以表示为

(7)

综上所述，以URLLC设备的子载波分配标识矩阵、mMTC设备的子载波分配标识矩阵和子载波n中各设备mk的发送功率pk,n视为优化变量，建立上行NOMA低功率传输优化模型，具体可以表示为

(8)

其中，C1为mMTC设备mk的传输速率需不小于Rk,min；C2为mMTC设备mk的最大传输功率限制Pk,max；C3为mMTC设备所对应的子载波分配情况的标识变量，其取值为离散值0或1；C4为单个子载波内叠加mMTC设备数应不大于Lu；C5为一个mMTC设备至多占用一个子载波；C6为保证SIC接收机正确接收的基本要求；C7为同一子载波内mMTC设备的接收功率应不大于URLLC设备所能承受的最大干扰；C8为URLLC设备所对应的子载波分配情况的标识变量，其取值为离散值0或1；C9为一个子载波包含的URLLC设备数量应不大于1；C10为一个URLLC设备至多只能接入到一个子载波；C11为当URLLC设备以pu,max发送时，Ru,min与URLLC设备所能承受的来自其它mMTC设备的干扰最大值In,max的约束关系。

2 算法设计

考虑到上述建立的最小化mMTC设备发送功率优化模型属于混合整数非线性规划(mixed integer nonlinear programming,MINLP) 问题[13]，因此为了对该模型进行求解，本文将此模型分成两个子问题：一是对URLLC设备进行子载波分配，二是对mMTC设备进行资源分配。

2.1 URLLC设备子载波分配算法

算法1： URLLC设备子载波分配算法

Output：Nbest,Ubest；

(1) BothNbest={nu1,…,nuU} andUbest={un1,…,unN}

are set none as initialization.

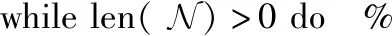
(5) end for

(6) foru,nin enumerate(Nbest) do %遍历Nbest

(7) ifunot inunthen

(8)un.append(u) %将u加到un中

(9) end if

(10) end for

(12) if len(un) == 1 then

(15) else if len(un)>1 then

(19) end if

(20) end for

(21)end while

2.2 基于AGA的mMTC资源分配算法

2.1小节针对URLLC设备制定了资源分配策略，本节设计mMTC设备的资源分配策略。

根据mMTC设备的通信特点，建立的最小化发送功率的优化模型表示为

(9)

s.t. C1, C2, C3, C4, C5, C6, C7

针对上述模型的NP难解性[13]，本文改进了传统AGA的惩罚函数，构建了惩罚系数自适应的适应度函数。本算法主要由“染色体编码”、“适应度计算”、“种群选择”、“交叉重组”和“染色体变异”5部分组成。

基于改进AGA的资源分配算法，具体执行流程如下所述：

(1)染色体编码：在现有的诸多进化算法中，染色体作为经过编码后的候选解。常用的染色体编码方式有二进制编码、灰度编码、实值编码等。本文为了降低染色体长度、提高算法收敛速度，同时尽量减少算法适应度计算过程中的约束条件，采取实值编码方式。具体地，将染色体分为两部分，M×N维的mMTC设备发送功率矩阵P和M×N维的mMTC设备子载波分配标识矩阵X，作为本节模型中的决策变量。如图1所示，功率矩阵P以实值编码的方式编码得到长度为M×N的染色体片段，该片段中每个基因取值为(0，Pmax]的连续值，子载波分配标识矩阵X经编码得到长度为M的染色体片段，此片段中每个基因取值为[0，N]的离散整数值。本算法的编码方式相比传统实值编码，染色体长度由2MN减少至MN+M，同时每个个体都满足了本模型中约束C2、C3、C5，达到了减少约束条件的目的。

图1 染色体结构

(2)适应度计算：在现有的进化算法中，每一代均维持一个种群，使用适应度函数来量化种群中的不同个体作为模型解的合适程度。本文的带约束的最小化功率模型，适应度函数不能直接由目标函数构成，需要通过约束违反程度矩阵CV和惩罚函数G(P,X)重新构建。

具体地，CV为Nind×Cnum维矩阵，该矩阵各列对应模型的各个约束条件，各行对应各个种群中的个体。其中，Nind为种群中的个体数，Cnum为约束条件个数。在本模型中改进的染色体编码方式使得约束C2、C3、C5在编码阶段已经被满足，其余约束条件的违反程度表示为

(10)

(11)

(12)

(13)

将上述式(10)～式(13)写成约束违反程度矩阵CV的形式，可以表示为

CV={CV1,CV4,CV6,CV7}

(14)

为了提高AGA算法的搜索能力，避免模型陷入局部最优，并保留种群中的次优个体，本文在文献[14]的基础上，改进了传统惩罚函数。在优化过程早期时，种群中没有或只有少量可行解，惩罚函数的惩罚系数应较高，指引搜索方向指向可行解区域。随着优化过程的不断推进，种群中可行解不断增加，惩罚系数应变小，使搜索重心从可行解转移到更优的目标解。当种群内全部为可行解时，惩罚系数变为0。同时，在同一种群不同个体中，满足约束条件较多的个体的惩罚系数应较小，使其有机会保留到下一代继续参与进化。具体地，本文将惩罚函数表示为

(15)

(16)

综上，个体的适应度函数Fitness表示为

Fitness=Gmax(P,X)-G(P,X)

(17)

其中，Gmax(P,X)为当代种群中个体惩罚函数的最大值。Fitness值越大，表示个体越接近最优解。下文将Fitness简记为f。

(3)种群选择：本文选择轮盘赌选择方式[14]，该个体适应度函数f的归一化值作为每个个体被选择的概率。具体的选择概率Ps表达式为

(18)

其中，∑f为当代种群中全部个体的适应度之和。每代种群的个体按照以上概率有放回地选取，并进行后续的优化过程。

(4) 交叉重组：在现有的进化算法中，交叉重组是指两个不同个体通过染色体的组合产生新的子代个体的过程。根据变量类型的不同，常见的重组方法可以分成两类：实数重组方法和离散重组方法。本模型中的染色体由功率矩阵P和子载波分配标识矩阵X经编码组成，即变量类型同时包含连续实数和离散整数，因此需要以混合交叉重组算法作为本模型的交叉重组方式。具体地，在本模型中，使用中间重组算法对取值为实数的功率变量进行重组，使用离散重组的方法对取值为离散整数的子载波分配标识变量进行重组。

根据中间重组算法得到的子代变量值，是以两个父代变量值为边界的区间内选取的。进一步地，子代的变量值表示为

(19)

其中，βi是[-d,1+d]区间内的随机数，表示随机均匀选择的比例因子。当d=0时，子代变量值的取值范围是严格以两个父代变量值为边界的区间。考虑到子代的大多数变量不产生在区域的边界上，子代变量的取值范围将随着进化代数的增加而不断缩小。因此为了避免这种情况，可以设置d=0.25，具体如图2所示。

图2 中间重组算法父代与子代变量取值范围对比

离散重组算法是在个体之间进行变量值的交换，在生成新子代个体之前，两父代个体中的每个变量都能等概率地选择其中一个作为子代的值。为了更为形象地表示重组操作，其结果的几何特征表现为图3所示的子代个体是父代所在超立方体的顶点处。

图3 离散重组算法可能的子代在解空间的位置

(5)染色体变异：在传统的进化算法中，子代个体通过变异生成具有某种新特征的个体。在本文所采用的AGA中，取值为连续实数类型的功率变量将采用高斯变异算法[15]，而取值为离散整数类型的标识变量则会采用整数值突变算法。

传统遗传算法的交叉概率和变异概率均是固定的，没考虑不同个体间适应度的差异。本算法使用自适应的交叉概率和变异概率，并将交叉概率Pc与变异概率Pm分别定义为

(20)

(21)

其中，favg表示当代种群平均适应度，fmax表示当代种群中全部个体的最大适应度，f′为两交叉父代个体的适应度中的较大值，f为变异个体的适应度，0

3 仿真结果与性能分析

3.1 仿真参数

通过实验仿真验证上述所提基于改进AGA的资源分配方案的性能。参照文献[6]中NOMA系统的仿真参数值，利用MATLAB工具进行仿真，每组参数均执行500次，每组参数结果取仿真结果的最优值。仿真参数设置见表1。

表1 仿真参数设置

如图4所示，横轴为种群进化代数，也可表示为算法迭代次数，纵轴为种群个体目标函数值，也可表示为系统功率值。为确定迭代次数上限，令M值为16、令U值为8、Ru,min值为120 kbps、Rm,min值为10 kbps，比较迭代次数分别为200和400时的算法收敛情况。图中可看出当最大迭代次数为200时，系统功率值虽然已低至0.3 W，但仍未收敛；当迭代次数为400时，系统功率值有明显的降低趋势，且图像已收敛。因此，本节后续实验的最大迭代次数均采用400。

图4 不同迭代次数的算法收敛情况对比

3.2 仿真结果分析

通过使用改进AGA进行仿真，并与传统AGA作比对，如图5所示。从图像可看出，在迭代初期两种算法收敛速度均较快。当迭代次数增加，系统功率会变小，收敛速度也变慢。改进后的AGA算法迭代约300次时，图像已经收敛，而传统AGA迭代约350次时收敛。由此可知，改进后的AGA提高了算法的收敛速度。

图5 传统AGA与改进后的AGA对比

为了验证所提算法的性能，将本文所提方案分别与子载波分配次优匹配(sub-optimal matching for subchannel assignment,SOMSA)方案[16]以及基于穷举搜索的非正交多址接入(exhaustive searching non-orthogonal multiple access,EX-NOMA)方案[4]进行对比。同时为了体现NOMA技术在mMTC场景中的优越性，使用现有的正交频分多址接入(optical frequency division multiple access, OFDMA)代表OMA技术进行对比分析。

图6将N设置为8，Rm,min设置为30 kbps，显示了接入设备数与系统功率的关系。可以看出，随着mMTC设备数的增加，系统功率也增加。这是因为当系统的总接入设备数量增加且N不变时，由于同一子载波内设备数增加，导致设备间干扰增加，为保证信号正确接收，设备需要以更大功率发送信号。该结果与文献[9]的结论是一致的。从图中可以看出，相比计算复杂度为O(N)的SOMSA方案，本文所提方案系统功率平均降低4.59 dBm。这是因为SOMSA方案仅考虑了用户与子载波之间的信道增益的关系，而本方案考虑了同子载波内mMTC设备间的干扰，并利用URLLC设备忍受的最大干扰对同一子载波内mMTC设备的功率做了限制。此外，本文所提方案在性能上接近于EX-NOMA方案，但EX-NOMA方案计算复杂度高达O(NM)，而本方案的计算复杂度低于O(N2)，远小于EX-NOMA方案。

图6 设备数与系统功率的关系

图7将N设置为8，M设置为16，表明了mMTC设备的传输速率需求与系统功率的关系。图像显示，SOMSA方案和本文所提基于AGA的NOMA方案表现均优于OFDMA方案。这是由于OMA方案中不同用户使用的是相互正交的资源，虽然减少了干扰，但是限制了速率，导致在相同传输速率需求下，OMA方案所需系统功率较高。NOMA方案可以在同一时频资源内为多个设备提供服务，从而能够满足更高的用户传输速率[5]。此外，本文所提方案的系统功率随着传输速率需求的增大而增加。这是为了满足较高的传输速率需求，以及SIC的正确接收，单个mMTC设备的发送功率会变大，系统功率也会变大。

图7 速率需求与系统功率的关系

图8将N设置为8，U设置为8，Ru,min设置为120 kbps，Rm,min设置为30 kbps，说明了MTC设备数与实际传输速率的关系。从图像可知，随着MTC设备数的增加，mMTC设备的实际传输速率有所下降，接近其最低速率要求，仿真验证该方案满足了mMTC设备低速率传输需求。而URLLC设备实际传输速率逐渐减小，这是因为MTC设备数的增加造成mMTC设备总功率增加，因此增加了URLLC设备受到的干扰，在URLLC设备发送功率不变的前提下，实际速率将会降低。

图8 设备数与实际传输速率的关系

4 结束语

针对不同通信需求的MTC设备混合接入的场景，本文提出了一种资源分配方案。优先为URLLC设备分配资源，保障其QoS；其次采用改进后的AGA对低速率传输的mMTC设备分配资源，降低其发送功率。具体对AGA改进的内容，具体包括：混合变量的染色体编码规则，以及自适应惩罚函数。改进后的算法不仅减少了变量数和约束矩阵维度，而且提高算法搜索能力，保留种群次优个体以避免较优解丢失。仿真结果表明，与传统AGA相比，改进后的AGA可以加快收敛速度，与SOMSA和EX-NOMA方案相比均有一定的优越性。