基于熵的混合属性聚类算法
邱保志,王志林
(郑州大学 信息工程学院,河南 郑州 450001)
0 引 言
聚类是数据挖掘的主要技术,它将相似的对象聚在一起,不相似的对象分离开来。聚类技术广泛用于医学、互联网、金融、天气预报等领域的数据分析。通常情况下,实际领域的数据对象是既包含数值属性又包含分类属性的混合属性数据。传统聚类算法大多都只能处理单一属性的数据,例如K-means[1]、DBSCAN[2]、DPC[3]等算法只能处理数值属性的数据,而K-modes[4]、Fuzzy K-modes[5]等只能处理分类属性的数据。所以,研究混合属性数据聚类技术对于实际领域的数据分析有重要的作用。
相似性的度量对聚类的研究有着非常重要的作用。文献[6]提到的K-prototypes算法以及文献[7]和文献[8]的算法是将混合属性相似性度量拆分为数值属性相似性和分类属性相似性分别度量,然后再组合成混合属性的相似性,但这样存在一个问题:数值属性相似性和分类属性相似性度量的差异会造成聚类效果不佳。例如在UCI数据集Credit approval中,前两个对象的第一个分类属性“A1”的二元化距离为1,而这两个对象的第15个数值属性“A15”的欧式距离为560,由于数值属性间的距离远大于分类属性之间的距离,导致数值属性之间的相似性权重很小,甚至会忽略掉数值属性所体现的相似性特征,进而导致聚类质量的下降。其中,文献[7]中对使用欧式距离度量相似性的数值属性采用标准化来处理这个问题,但是这样做仍然不能消除数值属性相似性度量和分类属性相似性度量的差异带来的聚类效果不佳问题,其算法中使用的二元化距离度量分类属性相似性会使得分类属性相似性的权重缩小。
针对混合属性中数值属性与分类属性相似性度量的差异问题,本文引入熵离散化技术,对混合属性数据集中的数值属性进行离散化,将数值属性转化为分类属性,在度量相似性时仅使用二元化距离度量,从而解决由于混合属性中数值属性相似性度量和分类属性相似性度量的差异而造成的聚类效果不佳问题,在聚类中通过随机选取初始簇中心并划分对象,然后迭代选择新的簇中心继续划分对象,直至目标函数收敛,形成最终聚类。
1 相关分析及定义

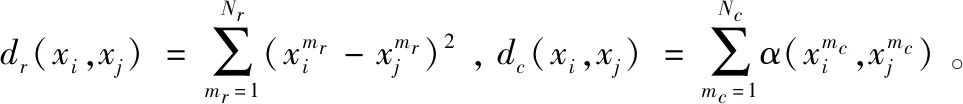
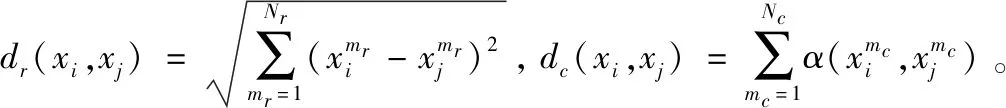



2 算法描述
2.1 数值属性离散化
离散化是指将连续属性的值域划分为若干个子区间,每个子区间对应一个离散值,最后将原始数据转化为离散值,其关键在于如何确定区间个数和划分点位置。
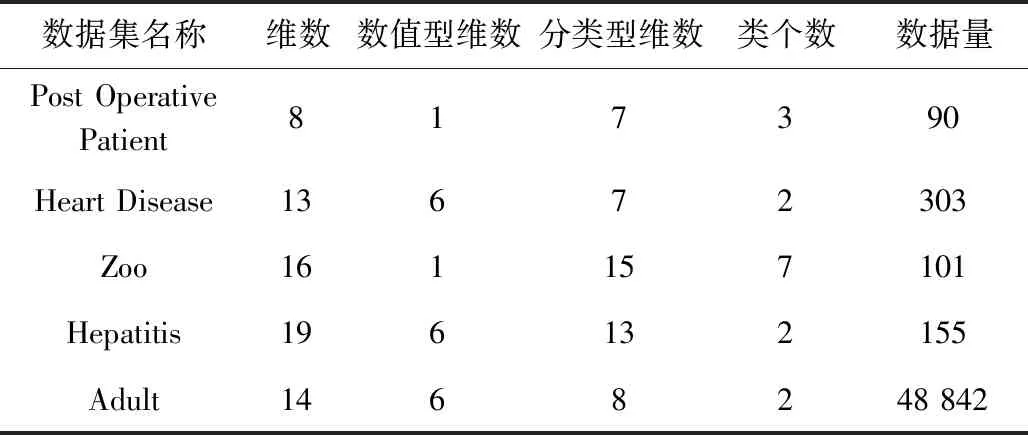
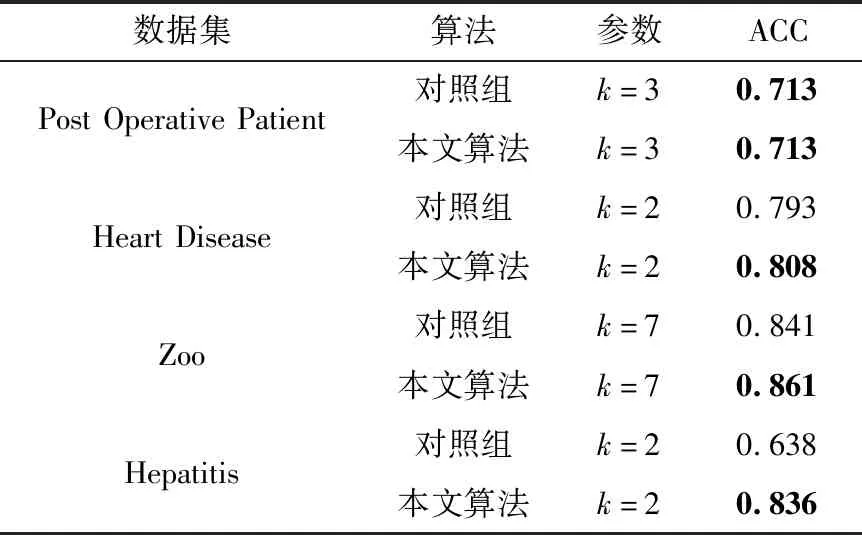
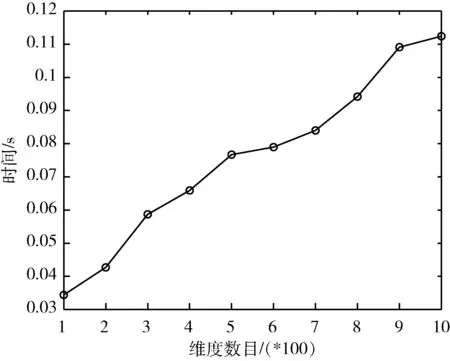
为了消除混合属性中数值属性与分类属性相似性度量的差异,引入熵离散化技术,将混合属性中的数值属性离散化,使用离散值来表示离散化后的数据,这样将数值属性转换为分类属性,从而使用一种相似性度量方式度量对象之间的相似性,消除度量差异。本文离散值选取离散划分的每个区间的最大值作为离散值,即f((a,b])=b,(a 若某个连续属性,值域为[value1,valuez],有z个不重复的属性值:value1、value2、 …、valuez, (value1 记区间个数为h, 1≤h≤n,n是样本总个数,根据定义1计算熵为H(h)。然后选择两个相邻区间进行合并,使得H(h)-H(h-1)最小,即合并前后熵差最小,若合并前后的区间使得H(h)-H(h-1)最小超过一对,则随机合并一对,然后重置划分点,接着对此步进行迭代,目标函数为[9] G(h)=(h0-1)H(h)-H(h0)(h-1) (1) 当满足G(h-1)≤G(h)停止迭代。式(1)中h0为初次划分的区间个数,H(h0)为初次划分区间的熵。离散化算法具体步骤如下: 算法名称: 基于熵的离散化算法 输入: 数据集D 输出:D中所有数值属性的区间划分点以及离散值 for(每个连续属性){ 对于z个不重复的属性值, 初始划分区间, 保存划分点; h=z; 利用定义1计算熵H(h); 令flag=TRUE;h0=h;H(h0)=H(h); G(h)=(h0-1)*H(h) -H(h0)*(h-1); while(flag){ 选择两个相邻区间进行合并, 使合并前后的熵差最小, 并重置划分点, 保存合并后的熵; 计算G(h-1)=(h0-1)*H(h-1) -H(h0)*((h-1)-1); ifG(h-1)>G(h){ h--; 重新计算每个区间对应的属性值个数以及总属性值个数;} else{ h--; 保存区间划分点, 选取区间最大值作为离散值; flag=FLASE;} } } 输出所有数值属性的区间划分点以及离散值; K-means算法只针对数值属性数据集,其选择簇中心的策略是初始随机选取,迭代时选取每个簇的属性值均值作为簇中心,当满足目标函数时停止迭代。K-modes算法只针对分类属性数据集,其选择簇中心的策略是初始随机选取,迭代时选取簇中频率最大的属性值作为新的簇中心,当满足目标函数时停止迭代。K-prototypes针对混合属性数据集,其选择簇中心的策略结合了K-means与K-modes的簇中心选取策略,其策略是初始随机选取,迭代时分为选取数值属性簇中心和分类属性簇中心,数值属性簇中心选取每个簇中的属性值均值作为簇中心,分类属性簇中心选取每个簇中属性值中出现频率最高的值作为簇中心,进而将两个簇中心组合形成混合属性的簇中心,当满足目标函数时停止迭代。 在上述算法选取簇中心策略的启示下,本文选取簇中心的策略是:先使用熵离散化技术将混合属性中的数值属性离散化,使得数值属性转换为分类属性,然后初始随机选取簇中心,迭代时选取每个属性的属性值在簇中频率最大的作为新的簇中心,当满足目标函数时停止迭代。 K-modes算法迭代时的目标函数[10]定义为 (2) 在K-modes算法进行迭代的时候,式(2)不再发生变化时停止迭代。式(2)是K-modes算法针对分类型数据时使用的目标函数,本文算法在混合属性数据中对数值属性进行离散化,完成了混合属性数据到单一的分类属性数据的转换,故在迭代时也使用式(2)作为本文算法的目标函数。 本文算法包括离散化、初始化簇中心、划分对象和迭代4个步骤。离散化使用熵进行离散区间划分,选取离散划分的每个区间的最大值作为离散值。在离散化后的数据集中随机选取k个对象初始化簇中心,使用定义2来度量对象的相似性并划分对象。然后选取新的簇中心进行迭代,当式(2)不再发生变化时停止迭代。 算法名称:基于熵的混合属性聚类算法 输入:数据集D,聚类个数k 输出:聚类结果 步骤1 使用熵对D中数值属性划分离散区间,选取区间最大值作为离散值。 步骤2 从离散化后的D中随机选取k个对象作为初始簇中心。 步骤3 使用定义2度量每个对象与簇中心的距离,并将每个对象划分到距离最小的簇中。 步骤4 重新计算簇中心,选择每个簇中数据属性中频率最高的属性值作为新的簇中心的属性取值。 步骤5 重复步骤3和步骤4,当目标函数F不再发生变化算法结束。 实验环境:CPU为Intel(R)core(TM)i5-4200M,内存为8 GB,操作系统windows10,编译环境为matlab2018a与java 1.8.0_221。 表1 数据集的基本信息 实验前对数据集进行预处理:①删除含有缺失值的数据,先删除数据对象中某维数据缺失过多的维,再删除某些维数据缺失的数据对象;②使用整数来代替分类属性数据,例如对于性别属性,0代表男性,1代表女性。 本文算法主要分为熵离散化、选取聚类中心、分派数据对象和迭代。为了验证在混合属性数据集中对数值属性进行离散化能提高聚类效果的有效性。本节将本文算法去掉熵离散化这一过程作为对照组和本文算法进行对照实验。选取的数据集为UCI中的Post Operative Patient、Heart Disease、Zoo和Hepatitis数据集,实验结果见表2。 表2 对照实验结果 在Heart Disease、Zoo和Hepatitis数据集中,本文算法聚类准确率(ACC)均高于对照组,这验证了在混合属性数据集中对数值属性进行离散化能够提高聚类效果的有效性。在Post Operative Patient数据集中。主要是因为在Post Operative Patient数据集中数值属性的不重复的属性值较少,在离散化之前可以视其为已经离散化后的数据集,故而本文算法聚类准确率(ACC)均与对照组持平。 为了验证本文算法对混合属性数据集聚类的有效性,选取了UCI中的Post Operative Patient、Heart Disease、Zoo和Hepatitis数据集,对比的混合属性聚类算法为K-prototypes[6]、EKP[8]、FKP-MD[8]和DP-MD-FN[11],实验结果见表3。 表3 混合属性数据集的聚类结果比较 在Post Operative Patient数据集中,本文算法聚类准确率(ACC)比K-prototypes高出0.092,比EKP高出0.035,比FKP-MD高0.18,比DP-MD-FN高0.012。在Heart Disease数据集中,本文算法聚类准确率(ACC)比K-prototypes高出0.23,比EKP高出0.283,比FKP-MD高0.283,比DP-MD-FN高0.049。在Zoo数据集中,本文算法聚类准确率(ACC)比K-prototypes高出0.128,比EKP高出0.247,比FKP-MD高0.029,比DP-MD-FN高0.019。在Hepatitis数据集中,本文算法聚类准确率(ACC)比K-prototypes高出0.186,比EKP高出0.05,比FKP-MD高0.06,比DP-MD-FN高0.05。 本文算法聚类准确率(ACC)均高于对比算法,主要原因是:对比算法在混合属性数据对象中,对数值属性与分类属性使用不同的距离度量对象相似性,这样存在的度量的差异会造成聚类准确率(ACC)不佳,本文算法引入熵离散化技术,将数值属性转换为分类属性,仅使用二元化距离度量相似性,解决了混合属性中数值属性相似性与分类属性相似性度量的差异问题,进而提高了聚类效果。 本节检测本文算法在数据对象的增多与数据维度增加的情况下的运行效率。但本文算法在数据对象增加时的运行效率主要被熵离散化的过程影响,而在这个离散化过程中的运行效率主要是被数值属性中不重复的属性值个数影响。因此本节可扩展性主要是检测算法在数值属性中不重复的属性值个数的增加和数据集维度增加时的运行效率。选取UCI数据集中的Adult数据集来抽取样本用来检测。Adult数据集中的第三条属性“fnlwgt”(数值属性)用来测量算法运行效率与在数值属性中不重复的属性值个数的关系,对“fnlwgt”属性值按照升序排列,然后选取不同的不重复属性值个数进行实验,结果如图1所示。选取Adult中前1000个对象的第二条属性“workclass”(分类属性)为样本,并将其扩充为高维度来检验算法在数据集维度增加时的运行效率,结果如图2所示。 图1 运行时间与数值属性中不重复的属性值个数的关系 图2 运行时间与维度数目的关系 从图1可以看出随着数值属性中不重复的属性值个数的增加,算法运行时间会快速增加,呈近指数形式,主要是因为本文采用熵对数值属性离散化,其离散化过程不需要人为添加参数,因此计算量较大,耗时增多。 从图2可以看出,数据集随着维度的增加并没有使得运行时间快速增加,可以得出本文算法运行效率被单一的维度增加影响并不大。 对于数据对象个数为n的数据集D,本文算法的时间复杂度主要与熵离散化、计算聚类中心、分派数据对象以及迭代次数有关。熵离散化的时间复杂度为O(Nr×n2),Nr为数值属性的个数。计算聚类中心的时间复杂度为O(n×q),其中q为数据的维数个数。分派的时间复杂度为O(n×q×k),k为聚类中心个数。根据上述分析算法的时间复杂度为O(Nn×n2+t×(n×q×k+n×q)),由于n×q×k>n×q,因此算法的时间复杂度为O(Nn×n2+t×(n×q×k)),t为迭代次数,本文算法主要在对数值属性进行离散化时会耗时较大,当数值属性中不重复的属性值个数越多,算法在运行过程中会耗时越多。 本文应用熵离散化技术,提出了基于熵的混合属性聚类算法。算法将混合属性中的数值属性转化为分类属性,使用单一的二元化距离度量对象之间的相似性,解决了因混合属性中数值属性与分类属性相似性度量的差异而造成的聚类效果不佳问题,实验验证了算法的有效性,与同类算法相比,有较高的聚类精度。该思想可为混合属性数据集的数据分析提供一种技术参考。2.2 算法步骤
3 实验结果及分析

3.1 离散化对聚类结果的影响
3.2 混合属性数据集

3.3 可扩展性

3.4 算法时间复杂度分析
4 结束语

