基于图约束联盟形成的社会共享乘车问题

朱丽华，龙海侠

(1.安阳工学院 计算机科学与信息工程学院，河南 安阳 455000；2.海南师范大学 信息科学技术学院，海南 海口 571158)

0 引 言

随着社会经济的发展和人们工作节奏步伐的加快，实时共享乘车(俗称拼车)正在迅速改变人们每天上下班往返或其它活动的交通出行方式。实时共享乘车最早起源于少数西方发达国家，然后迅速引进到国内。如美国著名的优步(Uber)和来福车(Lyft)，以及国内的滴滴、首约汽车和曹操出行等网约车公司。这种网约车公司的一个明显特征是要建立一个用户社区(或称共同体)，其中上下班往返的人(或称通勤者)可以对驾驶员/乘客进行评分，然后利用这些信息自动形成彼此了解/信任的通勤者群体，以降低相关的交通成本。本文将这个问题称为社会共享乘车(social sharing by car，SSC)问题。

本文将SSC问题转换为一个图约束联盟形成(graph constraint coalition formation，GCCF)问题，其中的通勤者(即乘客和司机)组成联盟(即加入一辆车)，以满足由社交网络施加的约束(即用户更愿意与他们的朋友一起加入一辆车)。具体来说，根据关于GCCF的相关文献[1,2]，只有当参与这个联盟的通勤者构成社交网络的一个连通子图时，认为一个联盟是可行的。

近年来，有一些文献针对SSC问题和GCCF问题进行研究；文献[3]将网约拼车匹配与路径优化问题考虑为静态车辆路径问题，构建了网约拼车匹配与路径优化模型；文献[4]提出了一种基于数据挖掘的城市上下班拼车线路优化拟合的方法；文献[5]研究了与拼车相关方面的计算，提出了一种模型来评价拼车计划；文献[6]分析了网约车服务流程及服务问题，并运用服务蓝图描绘网络约租车的全服务流程，而未就网约车服务建立一个定量化的数学模型；文献[7]提出了一种出租车综合推荐系统，设计了拼车情况下的费用分摊机制和拼车决策，达到使出租车司机利润提高和乘客的乘车费用降低的目标；与联盟形成相关的优化问题(即联盟结构生成)多年来也一直受研究人员所关注[8-10]，这些研究提供了一些最优解技术且能够提供质量保证的近似算法。但都不考虑限制可行联盟的图约束，因此，不能应用于GCCF问题；文献[11]提出了一种称为双层蚁群优化的随机算法来处理面向任务的联盟结构问题；文献[12]提出了各种联盟结构生成算法，以保证找到一个最优的联盟结构，并提出了基于协同联盟群的动态规划(synergy coalition group-based dynamic programming，SCGDP)算法，以保证一个最优联盟结构和一个最小核心稳定收益向量。但SCGDP算法要执行必要的搜索操作，以保证在给定的特征函数博弈中找到联盟，且这种方法效率的一个关键要素是寻找一个有效和高效的定界函数(也称限界函数或边界函数，即成长函数的上界)来剪枝搜索空间的重要部分的可能性。对于特定的特征函数来说，这样的定界函数很容易得到，可以分解为单调和反单调函数之和(m+a)。但SSC问题不具有这样的特性，因此本文针对文献[12]中提出的BBA算法进行扩展后作为本文SSC问题的求解技术，以便为大规模系统(例如多达2000个代理)提供解决方案。

本文首先提出了SSC优化问题的GCCF的定量化形式，然后将一个社会共享乘车问题转化为一个受社交网络约束的图约束联盟形成问题，从而建立起一个社会共享乘车问题模型，通过分析得到该问题模型的最佳联盟结构以及最优路径的计算，进而采用一种改进的分支定界方法来求解这个社会共享乘车问题，从而使得该系统的社会福利最大化。实验结果表明，本文的算法模型不仅可以改善社会福利，降低整个系统的成本，还能够为中等规模的系统快速高效地获得最优解且为大规模的系统获得质量保证的近似解。

1 GCCF问题及其求解

1.1 GCCF问题

联盟博弈或特征函数博弈由一组有限的玩家A和一个特征函数v：2A→R构成，特征函数将每个联盟C∈2A映射为它的值，这个值描述一组玩家通过形成一个联盟可以获得多少共同的收益；一个联盟结构(coalition structure，CS)是将一组代理划分为不相交的联盟，全部联盟结构的集合为∏(A)。一个联盟结构CS的价值确定为其构成联盟的价值之和，即

(1)

联盟形成问题(或联盟结构生成问题)以联盟博弈作为输入，目标是确定最有价值的联盟结构CS*，即

(2)

现在，给定一个图G=(A,E)，其中E⊆A×A是代理之间的边集，表示它们之间的关系，文献[1]认为，如果由一个联盟C所导出的G的子图中的全部成员都是连通的，就说一个联盟C是可行的，也就是说，如果对于来自a,b∈C的每一对玩家，在G中有一条不离开C就连接它们的路径。给定一个图G，可行的联盟集合为

FC(G)={C⊆A|C在G上导出的子图是连通的}

(3)

因此，图约束联盟形成博弈就是一个与图G一起的联盟博弈，如果C∈FC(G)，则联盟C就认为是可行的。在GCCF博弈中，如果每个联盟都是可行的，则联盟结构CS就认为是可行的，即

CS(G)={CS∈∏(A)|CS⊆FC(G)}

(4)

因此，一个GCCF问题的目标就是识别CS*，即最有价值的联盟结构

(5)

在定义了GCCF问题的基础上，下面给出求解GCCF问题的算法。

1.2 GCCF问题的求解

BBA是基于图G上的边收缩的概念，它表示与其事件顶点相关联的联盟的合并。这种操作可用于生成整个搜索空间CS(G)并将其组织为一个根树TG，根树TG可以以多项式存储需求遍历，以找到最优解。每个可行的联盟结构CS∈CS(G)仅用2色图GC表示一次，即每个TG节点一次，其中GC的节点代表CS的联盟，且边被标记为灰色(这种边仍然可以收缩)或黑色(意味之前的边收缩已经完成)，而且其端点不能在算法的以下阶段中处于相同的联盟中。图1(a)所示为一个2-色图的示例，图1(b)为收缩后的结构，其中边({A},{B})为黑色，因此，在算法的任何后续步骤中，都不可能收缩它。这个标记确保每个可行的联盟结构用TG表示而没有任何冗余。具体来说，给定一个表示可行的联盟结构CS的节点TG，对其子节点在相应的2-色图GC中收缩每个灰色节点进行评估，将根在CS的TG的子树称为ST(CS)。

图1 灰色边收缩示例

下面将一个SSC问题建模为一个GCCF问题并进行求解。

2 SSC问题的建模及其求解

2.1 SSC问题模型

本节来定义SSC问题模型。考虑一组乘客R={r1,…,rR}，其中R>0为总的乘客数，非空司机(驾驶员)集合D⊆R，D包括拥有一辆私家车的乘客，也把D称为代理。每个司机ri∈D都可以在他的车里接纳s(ri)个乘客(包括他自己在内)，其中函数s:R→N0给出每个车的座位数。如果ri∉D，则s(ri)=0。给定一组乘客C⊆R，如果下列约束成立，则称C是有效的。

约束1:|C|>1⟹∃ri∈C:s(ri)≥|C|，即对于全部乘客来说，至少有一个乘客有一辆有足够座位的汽车。

注意，这种约束允许一个乘客ri∉D可以是“单独的”，即如果可供使用的座位总数少于系统中的乘客总数，则这样的乘客可能需要使用付费的公共交通工具，支付车票的费用为k({ri})。定义函数k:R0→R-给出这种成本，其中R0={{ri}|ri∈R-D}是除司机外的全部“单独的”集合，因为假设这样的乘客总是更愿意使用公共交通工具。

现今，在几个拼车在线服务(例如滴滴、Lyft和Uber)中，通勤者可以声明他是否是司机或乘客，因此这两个集合是不相交的，而且一个有效的乘客集合C最多包含一个司机。因此，下列附加约束必须成立：

约束2:|C∩D|≤1，即每辆汽车的司机数目最多可为一人。

注意，尽管约束2是可选的，但它适用于目前的实际情况。尽管如此，由于本文的方法支持更一般的模型，所以也可以应用于这种约束不成立的情况。

考虑SSC问题发生中的地理环境的地图，用一个连通图M=(P,Q)来表示，其中P是地图的地理位置点的集合，Q是这些点之间的边的集合(每条边与一个正的权值关联)。在下文中，我们假设通过n个点的一条路径表示为一个元组P∈Pn，Pi表示在这样的一个元组中的第i个点。

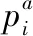
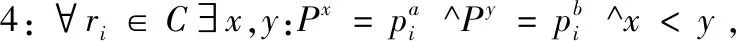
根据文献[5]，将有效乘客集合C的总成本v(C)定义为

(6)

式中：PC是C的最优路径，且t：Pn→R-，c：Pn→R-和f：Pn→R-为负的成本函数(由于本文考虑的是一个最大化问题，故将成本表示为负值，也可以表示为正值)，分别表示驶过一条给定路径的时间成本、认知成本(根据文献[5]，这个成本代表了司机在行驶途中所遭受的疲劳)和燃油成本。将这3个成本函数的总和表示为cost(·)。注意，如果C∩D=∅，则约束1规定，C由没有汽车的单个乘客构成，因此其成本用k(·)表示。此外，PC定义如下

(7)

如前所述，共享乘车的一个关键方面是社交网络G的存在，它限制了群体的形成。因此，SSC模型既考虑了关于可行联盟的定义，又将有效的座位集合定义为不违背约束1且其成员在G上导出一个连通子图的集合。这样，就把SSC问题转化为了一个GCCF问题，因为每个有效的乘客集合确实是一个联盟，而且v(·)给出了其联盟值。因此，CS*表示系统的最佳联盟结构，这种结构使得该系统的社会福利最大化(即总成本最小化)。然而，式(7)中的最优路径PC的计算是一个较难的问题，下节将阐明如何对成本函数进行合理假设来降低这种复杂性，从而使这种计算变得容易处理。

2.2 路径的计算

式(7)的计算复杂性来自于对成本函数t(·)、c(·)和f(·)的假设的缺失。然而，在许多城市道路中，汽车驶过一条路径(线路)的成本依赖于路径本身的长度，更长的路径通常会导致更高的成本。因此，假设t(·)、c(·)和f(·)为反单调函数，即假设两条路径Pi和Pj，如果Pi的长度大于Pj的长度，则t(Pi)

命题1 如果t(·)、c(·)和f(·)是反单调函数，则对于乘客集合C的最优路径PC就是最短路径Pi∈VP(C)。

证明：因为t(·)、c(·)和f(·)是反单调函数，则t(·)+c(·)+f(·)也是反单调函数，故命题显然成立。

给定一条路径P∈Pn，则把函数best:Pn→Pm定义为

(8)

式中：函数sp(·)给出了两点之间的最短路径，⊕表示元组的级联，m表示所有这些级联产生的点的数目。如果sp(·)采用Dijkstra算法实现，则函数best(·)可以在O((n-1)·(|Q|+(|P|log|P|)))计算完成。此外，如果M是一个欧几里德图，则sp(·)可以采用A*算法在O((n-1)·|Q|)内计算完成。

命题2 给定点的一个元组T，则best(T)是按顺序通过这些点的最短路径。

证明：用反证法。假设存在一条路径P′按顺序通过T的全部点，且P′比best(T)短，这样，T中必然存在两个连续点，即pi和pj，使得P′的从pi到pj的子路径比best(T)的从pi到pj的子路径短，这显然是矛盾的，因为它违背了best(T)的定义。

最后，给定乘客集合C，我们将VT(C)定义为元组的集合，该集合包含且仅包含其乘客的全部起点和目的地点(没有重复)，并且满足约束3和约束4。在此基础上，提出以下定理：

定理1给出了一种有效的算法来计算一组乘客的最优路径，假设成本函数是反单调的。其搜索空间是VT(C)，其大小明显小于式(7)的VP(C)，即|C|、|VT(C)|对于合理规模的乘客群体来说是可控的。实际上，对于|C|=5(即平均一辆汽车的座位数)，它仅为2520。

在下一节，我们将详细讨论如何将CFSS算法应用于解决上述定义的问题。

2.3 SSC问题的求解

为了求解SSC问题，必须将原始的BBA算法进行改进，以满足2.1中引入的附加约束。具体来说，为了保证约束1和约束2成立，必须避免形成无效的乘客集合联盟。这可以通过避免绿色边的收缩来实现，因为绿色边的收缩将导致违背这些约束。因此，这样的边必须用红色标记，即使没有访问相应的子树。事实上，这相当于遍历这样的搜索空间并丢弃它们可能包含的任何可能解，因为这样的解将违背上述约束之一。

提高BBA效率的关键是采用分支和定界搜索策略来剪枝搜索空间的有效部分。文献[12]针对一类特殊的特征函数即m+a函数提出了一种通用的定界技术。但式(6)定义的特征函数不是一个m+a函数，因为它依赖于PC，特别是依赖于乘客的起点和目的地点的实际位置。作为一个示例，图2所示为3个乘客的起点和目的地点，即R={r1,r2,r3}，其中只有r1拥有一辆自己的汽车，即D={r1}。为简化起见，假设v(C)等于PC的长度，且k({r2})=k({r3})=-1。

图2 3个乘客的起点和目的地点

下面提出可以在本文的共享乘车场景中使用的替代定界技术。

2.3.1 定界计算

在搜索树中，给定一个可行的联盟结构CS，现在来给出如何计算由ST(CS)中的特征函数所假定的值的上界M(CS)，即M(CS)≥V(CSi)∀CSi∈ST(CS)。这个值可用于避免访问ST(CS)，如果M(CS)不大于当前的最好解。

首先，提出一种方法来计算在约束2成立情况下的M(CS)。在这些情况下，不可能合并两个包含司机的联盟，因为只有不拥有汽车的单个乘客才允许加入到现有的组。注意，如果考虑反单调的成本函数，则增加一个乘客到一辆车只会带来更大的成本，因此，全部车辆(即所有包含司机的联盟)的成本之和仅在增加乘客之后才能增加，更一般地，如果cost(·)是一个反单调函数且约束2成立，则

M(CS)=∑C∈Rd(CS)v(C)

(9)

式中：Rd(CS)={C∈CS|C∩D≠∅}。

(10)

现在可以提出以下命题：

命题3 如果cost(·)是一个反单调函数，则

(11)

证明：这个证明可以从三角形不等式的旅行商问题即TSP问题(traveling salesman problem，TSP)的界的证明中得到[13,14]。

上述结果能够确定ST(CS)中的所有联盟结构的界V(·)，也可以用来计算具有质量保证的近似解。

2.3.2 近似解

上一节描述的定界技术允许对搜索空间的有效部分进行剪枝，从而为中等规模的系统(如多达100个代理)提供最优解。然而，实际的应用可能涉及数千个代理的共同体，且遵循实时拼车的概念，因此系统应该能够在短时间内提供解决方案，即对于实际应用来说，必须考虑近似解。上一节讨论的定界技术可以用来实现近似的SSC问题。具体而言，就是在一段时间ts后，停止搜索过程，并计算搜索树的全部叶子结构的界M(CS)，这些值中的最大值就是在ts中找到的近似解的一个容许界。

3 实验结果

为了对本文所提出算法的有效性进行验证，软件上采用C++语言并结合Matlab7.0，硬件在Pentium IV 2.0 GHz(512 M内存)的PC机和Windows XP操作系统环境下完成。

3.1 算法性能评价目标及数据集

评价算法性能的主要目标有：①采用本文提出的共享乘车算法的社会福利改善；②从运行时间和可扩展性方面评价本文提出的最优算法性能；③本文算法扩展到大量代理(即多达2000 个代理)时所能提供的近似性能和保证。

实验采用真实的数据集，包括空间数据和社会数据。具体而言，采用的地图M=(P,Q)是北京城市的真实写照，其中|P|=8330个点，|Q|=13290条边，相当于每10 m一个点的平均分辨率。这个地图是从微软提供的地球生命(GeoLife)[15]数据集得到的，它包括17 621个轨迹，总距离约为120万km，由具有多种采样率的不同GPS记录器和GPS电话记录得到。在实验中，还将这个轨迹池用来对随机路径进行采样，以用于提供乘客的起点和目的地点；此外，在每个实验中，图G是Twitter社交图大爬行的子图，之所以采用Twitter数据集，是因为它是免费提供的，不受隐私限制(不像Facebook)。具体而言，G是通过一个标准算法[16]从一个较大的图中提取一个子图得到，即从整个图的一个随机节点开始遍历，然后将每个节点和对应的弧添加到G中，直至得到所需的节点数为止。

一方面，由于司机是少数，且在城市环境中很少存在疲劳驾驶，故其认知成本可以不加考虑；另一方面，由于全部拼车乘客的时间都是预先计划好的，且整个时间的长短决定了路径的长短，从而直接影响汽车的燃料费用，故在实验中，为简化起见，采用一个仅虑燃料费用的成本模型，即

(12)

全部实验都在考虑约束2(即司机总是开车)上进行，因为这样可以模拟现实中的在线服务，例如滴滴打车、Lyft和Uber；每个实验在20个随机情形下重复进行。

3.2 社会福利的改善

社会福利的改善是基于每个乘客采用各自的交通工具(即不拼车)方案相比时社会福利的改善(即整个系统的成本减少)，这可以表明在采用本文的拼车算法时，整个用户社区(共同体)可以获得的收益。具体来说，将社会福利改善定义为

100·|[V(CS*)-V(R0)]/V(R0)|

(13)

式中：V(CS*)为采用本文拼车算法时获得最优解时的成本，V(R0)为每个乘客采用各自的交通工具(即不拼车)方案时的成本。福利改善的程度受系统中司机所占百分比(即代理|D|)的影响，因为这决定了可供使用的座位数量，以及在不需要采用公共交通工具的情况下，可以共享汽车的乘客数量。图3所示为得到的实验结果。从图3可见，一方面，随着更多司机的出现，一个乘客更有可能加入一辆其路径更接近他/她的车，所以社会福利的改善会随之而增加。如当总的乘客只有10%拥有车(即司机百分比|D|=10%)时，平均成本减少是23.5%，当有半数的乘客拥有汽车(即司机百分比|D|=50%)时，平均成本减少达到36.3%；另一方面，如果大多数乘客拥有自己的汽车，如司机百分比超过80%时，那么共享拼车就不是很有效了，这时社会福利的改善反而减少，因为没有车的乘客数量大大减少，他们可以从与有车的司机共享他们的通勤中获益。

图3 社会福利的改善

为了进一步表明本文算法的有效性，将它与文献[12]的算法和一个典型的贪婪算法相比较。尽管文献[12]考虑了协同图上的联盟结构生成和分支定界，但这种算法必须要寻找一个有效和高效的定界函数来剪枝搜索空间的重要部分。对于特定的特征函数来说，这样的定界函数很容易得到，而SSC问题不具有这样的特性；在贪婪算法中，每个司机都选择它的下一站作为它的当前乘客的目的地点和剩余乘客的起点之间的最近点。这个选择考虑了社交网络的制约，避免了不可行联盟的形成。3种算法的结果如图3所示，可见，无论司机百分比|D|处于较低还是较高时，本文算法获得的社会福利的改善始终高于文献[12]的算法和贪婪算法。特别是当大多数乘客拥有自己的车时，文献[12]的算法和贪婪算法得到的解的成本比本文的算法要高，所以社会福利的改善下降更多。只有很少的乘客不拥有自己的车的情况下，文献[12]的算法和贪婪算法表现稍好，因为它可能会在考虑最优的联盟之前将一名乘客分配给一个次优的联盟。

3.3 最优算法的运行时间和可扩展性

图4所示为当代理数量|D|从30增加到100时采用本文算法和文献[12]算法计算最优解所需要的运行时间。在3种情形下对算法进行了测试，即在低(|D|=10%)、中(|D|=50%)和高(|D|=80%)的司机百分比下。从图4可以看到，该参数对两种算法的性能都有明显影响。事实上，搜索空间的大小取决于可用的座位数量(即搜索空间在可用的座位数量百分比较低时减小)，以及没有自己的汽车而能够从共享他们的通勤中受益的乘客人数(即搜索空间当大多数代理拥有自己的汽车时减小)，这与3.2得到的社会福利改善的结果是一致的。由于在任何情况下，本文算法都可以在合理的时间内解决有100个代理的系统，如在|D|=50%的情况下最多大约2 h，这个运行时间适用于一天前或一周前请求的服务(例如滴滴和Lyft)。且由于本文的定界技术允许剪枝搜索空间的有效部分，所以本文算法的性能不但是合理的，而且相比于文献[12]的算法，在获得最优解时所需要的运行时间始终小于文献[12]的算法。

图4 计算最优解所需的运行时间

3.4 近似性能

图5所示为当本文方法用于求解|R|∈{500,1000,2000}的大型系统时得到的近似比(即上界值与近似解的比值)。具体来说，当采用2.3节描述的近似技术时，在ts=100s后停止搜索树的遍历。实验结果表明，对于|R|=500和|D|=80%来说，所得到的上界仅比在限定时间内得到的解高6.7%，而当|R|=2000和|D|=50%时，其最大值为41%，即在最坏的情况下，得到的近似比为1.41，因此这个解至少为最优解的71%。

图5 解的近似比

4 结束语

本文对社会共享乘车(俗称拼车)问题进行了研究，首先将其建模为一个GCCF问题，并针对GCCF扩展了一种BBA算法来求解这个问题。实证评价表明，本文的拼车算法不仅可以改善社会福利，降低整个系统的成本，而且还可以计算出具有良好质量保证(即在最坏情况下近似比为1.41)的大型系统(即多达2000 个代理)的解，因此适合于实际应用。

未来的研究将着眼于扩展本文的算法模型，包括采用交通信息、乘客时间约束以及多跳拼车[17]的更复杂的线路情形。