面向空铁联运的枢纽航线网络优化模型

吕宗磊，吴志帅，徐 涛,3，卢 敏,3

(1.中国民航大学 计算机科学与技术学院，天津 300300；2.中国民航大学 民航信息技术科研基地，天津 300300；3.中国民航信息网络股份有限公司 民航旅客服务智能化应用技术重点实验室，北京 101318)

0 引 言

传统的枢纽航线网络结构容易引起枢纽机场的拥堵问题。面向空铁联运的枢纽航线网络为解决枢纽机场拥堵问题，将高铁节点作为非枢纽节点加入到枢纽航线网络中，其实质上是对枢纽航线网络结构的一种优化。网络结构的优化需要考虑枢纽机场的拥堵问题、模型求解、航线网络相关业务问题，具体分析如下。首先，航线网络相关业务问题的改变会影响及到枢纽航线网络结构的变化。Ta-Hui Yang等[1]对传统枢纽航线网络结构进行优化，然而其优化网络结构与国内航线网络结构特点不同；陈婉莹[2]考虑了旅游型旅客对枢纽航线网络的影响，不足之处是枢纽机场的容量约束未被考虑；黄娟等[3]提出将空铁联运运用到货运方面，并对其进行货运量预测，但是并未涉及网络结构的优化和客运流量的应用。徐凤等[4]提出包含直航的航线网络结构，虽贴近国内航线业务但是并未对多种运输方式进行考虑。对于拥堵问题，多数研究从经济因素分析造成拥堵问题的原因[5-7]。Wu W等[8]针对国内航线网络提出了区域枢纽概念，为解决拥堵问题奠定了基础。最后，常见的启发式算法[9]多为求解优化模型的主要方法。然而，随着模型涉及因素变多和数据量的剧增，模型的变量和求解复杂度也随之增加。故此，本文建立的包含3种运输方式的多维度多下标变量和多约束条件的网络优化模型，其求解具有一定难度。通过创新性地使用矩阵表示法改变变量存储结构，并且结合禁忌搜索算法，有效地降低了求解复杂度。同时，能够明显缓解了枢纽机场的拥堵问题。

1 问题描述及定义

航线网络由机场节点、机场间航线及航线客流量组成，分别对应航线网络的节点、边以及边的权值。航线网络中的机场可被划分为枢纽机场和非枢纽机场两类[1]。由枢纽机场和非枢纽机场组成的航线网络为枢纽航线网络，且规定非枢纽机场之间不允许直航，需要通过枢纽机场中转，枢纽机场之间允许直航。

枢纽航线网络优化是在固定机场间客流量和机场容量的前提下，针对面向空铁联运的枢纽航线网络和严格意义枢纽航线网络以及非严格意的枢纽航线网络进行相关约束，最终生成最优的线路及流量分配方案。

严格的枢纽航线网络是在枢纽航线网络结构上对客流量的枢纽转运次数进行限制，即非枢纽机场的客流量经过枢纽机场节点数不能超过两个。严格的枢纽航线网络如图1所示。

图1 严格的枢纽航线网络

图1中，航线i1-k2-i3是(单)枢纽转运航线，非枢纽机场i1、i3通过枢纽机场k2中转；航线i2-k1-k3-j1,是(双)枢纽转运航线，非枢纽机场i2和j1经过枢纽机场k1和k3转运。另外，枢纽节点的航线为枢纽间航线。

严格的枢纽航线网络进行放松直航条件，形成非严格的枢纽航线网络。图2为非严格的枢纽航线网络示意图。其中，线路i1-i2代表始发机场i1直接到达目的机场i2的直航航线，即非枢纽机场节点间允许有直航航线，图2中枢纽转运航线同图1。

图2 非严格的枢纽航线网络

非严格的枢纽航线网络中加入高铁节点，并将其作为非枢纽节点。基于非严格的枢纽航线网络对面向空铁联运的枢纽航线网络进行定义：高铁节点(即非枢纽节点)可以连接枢纽节点和非枢纽节点；故此，此种网络结构包含3种运输方式，即高铁直达和联运运输以及直航。图3为面向空铁联运的枢纽航线网络示意图。非枢纽高铁节点i2和j2间的线路为高铁直达线路；线路j3-k3-j2表示非枢纽高铁节点j2和枢纽机场k3间为空铁联运线路，非枢机场铁节点j3和枢纽机场k3间为枢纽转运线路。

图3 面向空铁联运的枢纽航线网络

图3中的节点是同时建有高铁站和机场的城市，且网络中能够包含多种交通运输方式，故基于此种网络结构解决枢纽机场的拥堵问题。Ozgunkibiroglu C等[9]通过幂律函数的形式来描述拥堵成本，即拥堵成本与拥堵流量的关系

Γk=e(gk)b

(1)

其中，枢纽机场k的拥堵成本为Γk，始发-目的城市节点对i和j经过枢纽机场k的实际客流量为gk，e、b均是正数。

改进拥堵成本可以进一步减缓枢纽机场的拥堵问题。超出机场容量阈值的部分客流量进行拥堵成本计算[9]，如下式

Γk=e(gk-Ok)b

(2)

其中，Ok为枢纽机场k的容量阈值，(gk-Ok)为拥堵流量，表示始发-目的城市节点对i和j所经过枢纽机场k的客流量超出其容量阈值的部分。

2 面向空铁联运的枢纽航线网络优化模型构建

该优化模型以网络的总成本为优化目标，对运输方式的客流量和成本进行约束，优化模型如下：

(1)优化目标

(3)

(4)

其中，t1,t2∈T,T={1,2}

(5)

(2)高铁线路和直航约束：为缓解机场线路客流量拥堵，将部分拥堵流量分配给高铁线路以及非枢纽机场间的直航航线，需要保证分配出去的流量不超过拥堵流量，且运输成本要低于拥堵成本。约束如下

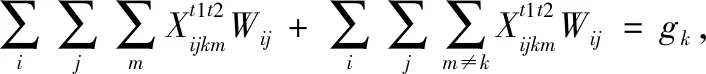
(6)

(7)

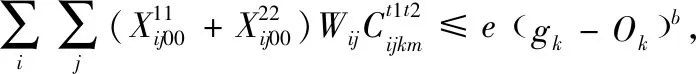
(8)

(9)

(10)

(11)

(12)

3 优化模型求解算法

3.1 禁忌搜索算法

优化模型的决策变量表示了运输线路所经过的节点和运输方式，是六维多角标的复杂变量。而对于具有较多节点数的大型网络存在解空间较大，变量所需存储空间较大，求解复杂度较高，且容易陷入局部最优解等情况。本文首先针对高纬度的多角标变量进行降维简化表示，然后采用具有灵活的记忆功能和藐视准则的禁忌搜索算法，减少够跳出局部最优解的概率。

3.1.1 初始解的表示方法与生成

潜在枢纽城市节点集合U生成枢纽城市的初始位置集合。由集合U随机生成P个枢纽城市节点，组成一个1×n的矩阵O，该矩阵中P个元素为1，其余元素均为0。其中，n为城市节点总数目，P为枢纽城市节点数目

(13)

本模型采用优化节点间的客流分配方案来解决运输路径问题。路径分配问题的解由矩阵Xn×n表示，矩阵中的元素为城市节点对，每个城市节点对由3个列向量β1、β2、β3组成矩阵(xij)n×3。其中，β1为枢纽节点列向量，向量中元素值为0则为非枢纽城市，为1的值为枢纽城市且数量最多为两个；转运方式列向量β2与β3表示枢纽城市和非枢纽城市间的运输方式，0表示该节点未被选择，1表示选择该节点并以高铁方式运输，2表示选择该节点并以民航方式运输。详见式(14)、式(15)

(14)

(15)

其中，β1⊂(O1×n)T且K≤2，β2、β3取值集合为{0,1,2}。

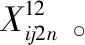
表1 初始解生成算法(算法1)

表1(续)

上述初始解算法可以将六维多角度变量转换为二维矩阵进行变量存储，大大降低了模型求解的运行时间和空间复杂度。

3.1.2 邻域结构设置

由于算法1是基于潜在枢纽集合生成初始解集，不能全面地表示全部解。因此采用领域搜索策略[10]扩大解的搜索空间，即枢纽节点和非枢纽节点之间成对交换。如图4所示。

图4 交换移动过程

由图4可知，枢纽节点D和E组成初始可行解，交换非枢纽解A和枢纽节点E，则枢纽节点和非枢纽节点组成的邻域空间变大，进而解的搜索空间覆盖更全面。

3.1.3 适应度值选择

面向空铁联运的枢纽航线网络的优化模型，是一个包含3种运输方式的多约束模型。然而，多约束模型容易导致求解速度慢甚至无解等问题[11]。因此，为了快速生成初始解，本文在生成初始解过程中未考虑式(11)的约束条件。同时，适应度函数对不满足式(11)的解进行惩罚，具体惩罚函数见式(16)

q=γ·max{R,0}

(16)

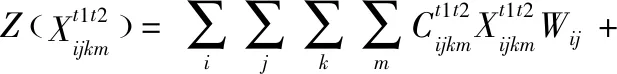
(17)

3.1.4 禁忌表设置

禁忌表记录每次移动和交换的节点，其长度计算方法见式(18)。以适应度值为藐视准则：若当前解的适应度值优于最优值，则将当前值更新为最优值；固定步长为终止准则，即步长次数达到预设最大值则终止计算

(18)

3.2 基于禁忌搜索算法求解枢纽航线网络优化模型

为解决初始解生成算法的初始解集覆盖不全面的问题，将初始解集经过禁忌搜索算法优化更新，搜索并输出算法最优解。算法的求解过程见表2。

表2 面向空铁联运的枢纽航线网络优化算法(算法2)

4 实验及结果分析

4.1 实验数据及参数

4.1.1 实验数据

本文实验数据来自国内16个城市节点间的运输线路(民航数据来源：民航局官方文件《从统计看民航2017》、《2017年民航行业发展统计公报》；高铁数据来源：www.12306.cn、www.ctrip.com；)的数据集，包括109个民航城市节点对和212个高铁城市节点对的线路数据，主要有机场和高铁节点间客流量、成本等数据。具体数据见表3、表4。

表3 城市对数据示例

表4 城市(机场)数据示例

4.1.2 实验参数设置

本文实验参数设置见表5，其中枢纽机场数目与禁忌表长度、候选解个数依次对应。

表5 实验参数设置

4.1.3 评价指标

本文对枢纽航线网络的评价从优化模型、枢纽机场拥堵程度、网络结构3个维度展开，分别对应网络最优成本、枢纽流量分担率、枢纽负荷3种评价指标[12]。

网络最优成本由枢纽航线网络优化模型的适应度值来衡量，即适应度值越低，网络结构优化效果越好，网络最优成本越低，计算公式见式(17)。

枢纽流量分担率表示通过枢纽机场k的客流量占枢纽航线网络总客流量的比例。机场的枢纽流量分担率越均衡，则表示枢纽机场间的客流量分配越合理，枢纽机场超负荷运行的情况越少，进而表明枢纽机场发生拥堵问题的可能性越低，该网络结构更加合理。具体计算公式见式(19)

(19)

判断枢纽机场是否存在拥堵问题的标准为枢纽负荷率。枢纽负荷率为流经枢纽机场k的实际客流量gk与枢纽机场容量阈值Ok的比值。具体见式(20)、式(21)

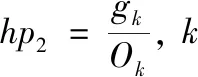
(20)

(21)

4.2 实验分析

4.2.1 实验结果分析

通过对3种航线网络结构建模实验，并对通过3种评价指标进行量化对比分析，具体见表6～表8。

表8 枢纽负荷率

由表6可知,基于不同的枢纽数目(本文以3，4，5为例)的3种航线网络结构进行对比，面向空铁联运的枢纽航线网络结构的最优成本最低，非严格的枢纽航线网络最优成本次低，严格的枢纽航线网络最优成本最高；因为面向空铁联运的枢纽航线网络增加的运输方式、线路科学地优化了枢纽航线网络结构，使得运输线路和客流量更加合理，进而降低了网络最优成本。

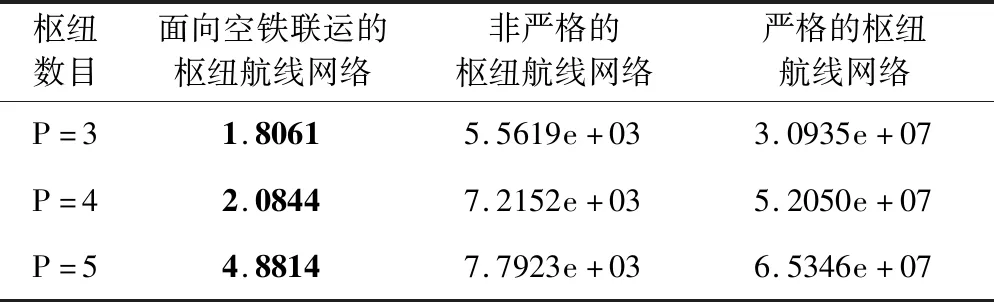
表6 网络最优成本/百万元

由表7可知,基于不同的枢纽数目(本文以3，4，5为例)的3种航线网络结构进行对比，面向空铁联运的枢纽航线网络结构的枢纽流量分担率与平均分担率最接近，枢纽分担率最均衡；非严格的枢纽航线网络结构分担率较均衡，但是仍有部分枢纽机场的分担率较高；严格的枢纽航线网络结构存在枢纽流量分担率不均衡现象，部分枢纽承担客流量较大导致拥堵甚至严重拥堵问题。由此可知，优化枢纽航线网络可以均衡枢纽之间的流量。

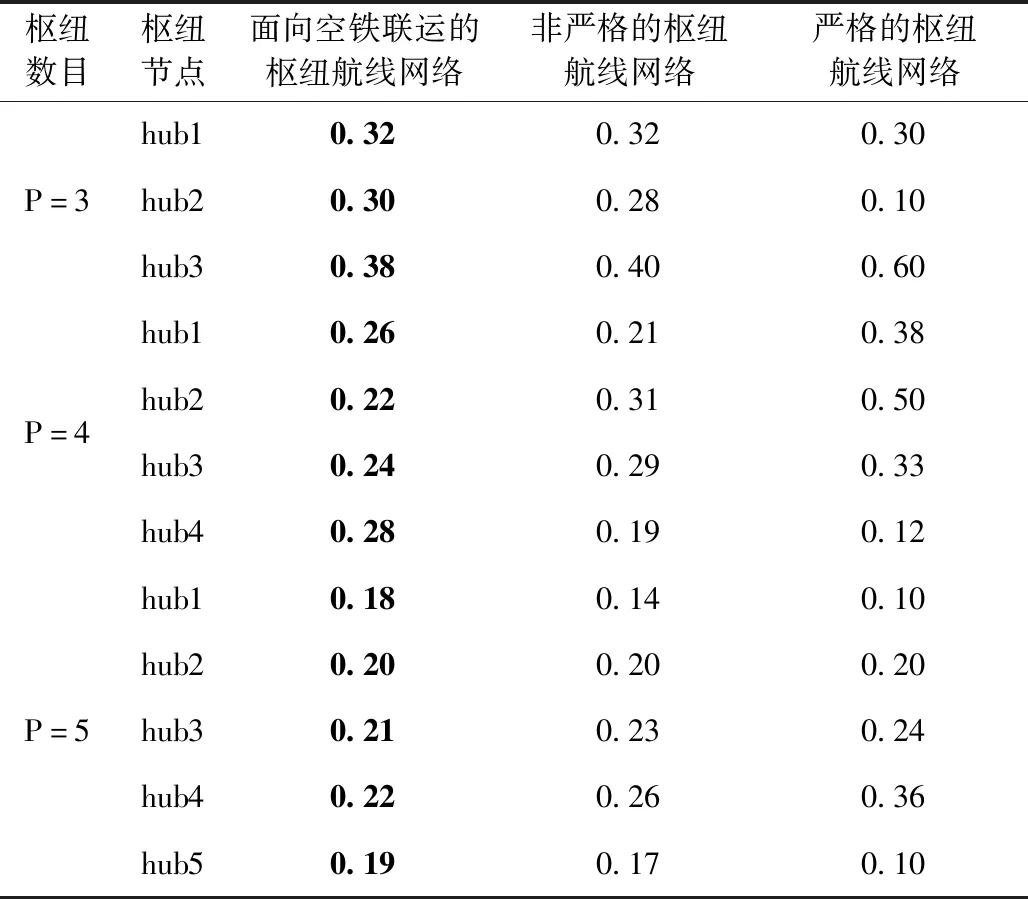
表7 枢纽流量分担率

结合表8和式(21)可知，基于不同的枢纽数目(本文以3，4，5为例)的3种航线网络结构进行对比，非严格的枢纽航线网络和面向空铁联运的枢纽航线网络不存在枢纽拥堵，严格的枢纽航线网络中的枢纽存在枢纽拥堵。究其原因，严格枢纽航线网络结构的枢纽机场存在严重的拥堵问题，导致枢纽机场实际承载容量远超阈值容量；非严格的枢纽航线网络结构引入了直航航线，分担了枢纽机场的拥堵流量；引入高铁线路和联运航线进一步优化航线网络结构，结果数据表明枢纽机场负荷率更加有效地下降。也即，本文提出的面向空铁联运的枢纽航线网络结构能够合理有效地分配枢纽机场客流量，减缓枢纽机场的拥堵问题。

4.2.2 算法分析

为保证模型求解结果的准确性，对求解算法的收敛性和稳定性进行了分析。首先，将禁忌搜索算法中的粒子迭代更新100次，查看每次迭代后的适应度函数值的变化趋势，进而分析算法的收敛性；然后，禁忌搜索算法整体运行100次，查看每次运行后的适应度函数值的分布范围，进而分析算法的稳定性。详细算法分析结果如图5、图6所示。

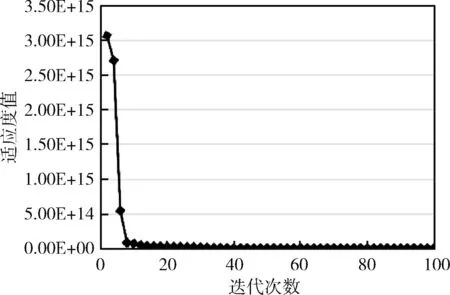
图5 算法收敛性分析

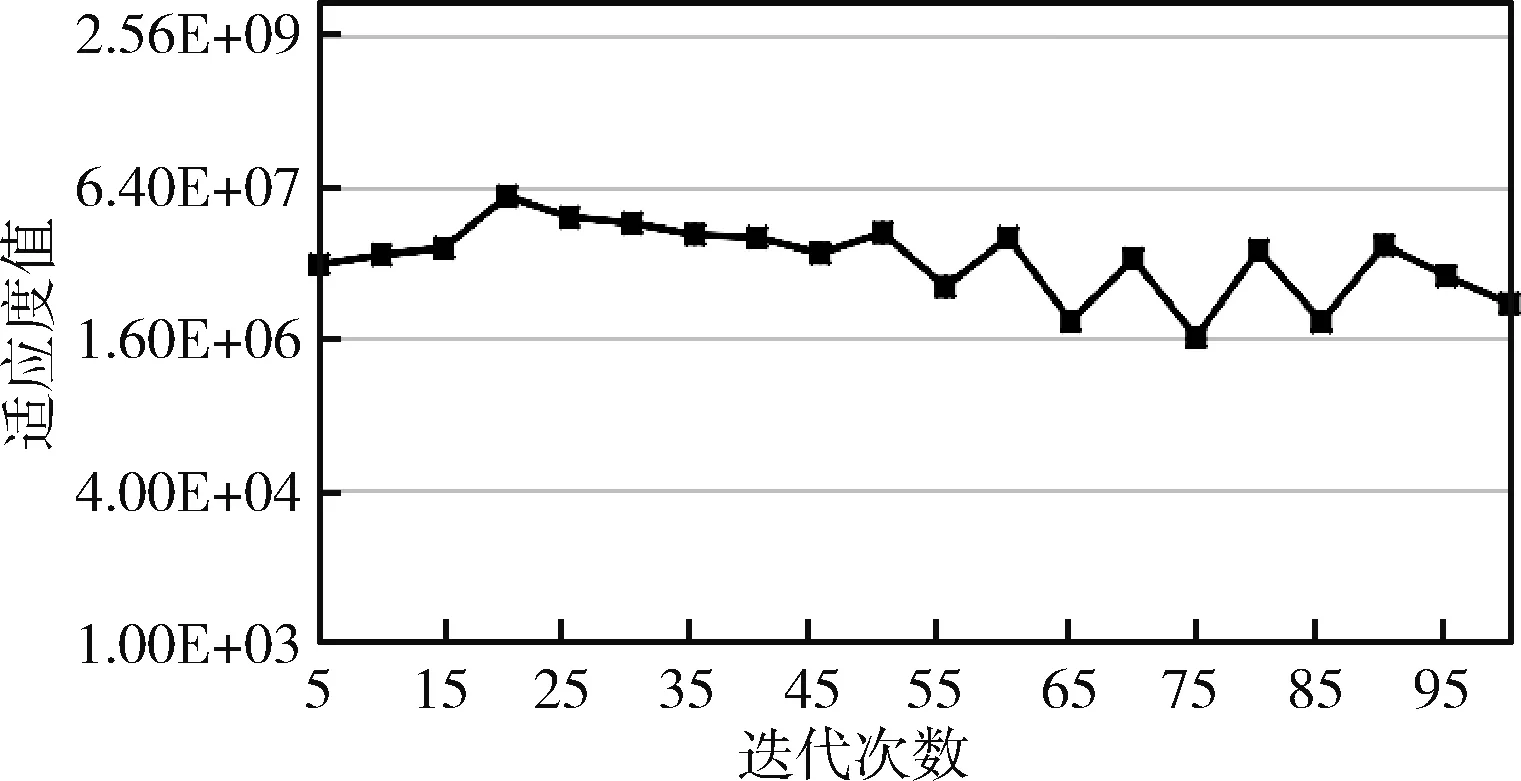
图6 算法稳定性分析

收敛性表示适应度值随着内部迭代次数的增加而变化的趋势。从图5可以看出，经过前10次迭代后，适应度值迅速下降；然后在第10至45次内，适应度值收敛速度变慢；最后，在第46次后适应度值趋于稳定。上述分析结果表明该算法在本数据集上能够收敛，进而得到最优解。稳定性表示随着外部迭代次数增加，适应度值的波动范围。从图6可以看出，经过100次运行禁忌搜索算法得到的适应度值，分布范围比较稳定且十分接近，均分布在区间[1.60×106～6.04×107]内，由此可知，该求解算法具备良好的稳定性，求解结果具有较高的准确性。

5 结束语

现有枢纽航线网结构络研究多数是基于严格的枢纽航线网络结构进行优化的，与国内城市节点多、分布广等特点不符合，而且易造成枢纽机场的拥堵问题。本文在枢纽航线网络结构方面，采用引入高铁和直航线路优化网络结构，合理分配客流量。在模型求解方面，采用初始解生成算法和禁忌搜索算法全面高效地搜索最优解；另外，巧妙地利用了矩阵表示法，既合理分配了航线运输方式和客流量，又很大程度上减少了求解的复杂度。经实验结果分析可知：与另外两种结构的航线网络相比，基于面向空铁联运的枢纽航线网络结构的优化模型具备较低的网络最优成本，并且还能够有效地减缓枢纽机场的拥堵问题。