基于PSO-LSSVM的热电偶非线性校正方法研究

张 龙,张宝国,张继军,张东亮,孔德骞

(西北核技术研究所，陕西 西安 710024)

0 引 言

在有限空间爆炸实验中，准确测量爆炸场的温度参数对于研究爆炸过程的传热规律、分析爆生气体的热力学状态等具有非常重要的意义[1-2]。目前，爆炸温度测量多采用基于热电偶温度传感器的接触式测温法。然而在测温范围较大的爆炸温度测量中，热电偶的输出热电势与输入温度之间存在较为严重的非线性问题，且基于现场总线的数据采集系统也表现出非线性特性。为提高测量结果的准确性，有必要对应用于爆炸温度测量中的热电偶进行非线性校正。

当前，对传感器进行非线性校正的方法主要有硬件电路补偿法和软件校正法。在实际应用中，硬件补偿电路产生的温度漂移、增益误差等影响了非线性校正的精度，同时也增加了测试系统的成本。传统的基于线性插值、曲线拟合等方法的软件补偿法也存在诸多缺陷，难以获得理想的补偿效果[3-4]。近年来，神经网络、支持向量机、正交多项式等方法被广泛应用于传感器非线性校正中[5-6]。其中，BP神经网络受限于经验风险最小化原则，在小样本情况下，容易导致过学习现象，且收敛过程易陷入局部极小值，无法获得全局最优解；基于遗传算法的校正方法搜索速度较慢，且寻优结果对初始种群的选取表现出一定的依赖性。相比之下，基于最小二乘支持向量机的非线性校正方法有效解决了过学习和局部极小问题，表现出较强的鲁棒性和泛化能力，是非线性系统建模的有效方法。

然而，影响最小二乘支持向量机优化效果的惩罚系数及核函数参数的选取问题目前尚无统一的解决方法。传统的基于经验的参数选取方法主观性太强，难以获得最优的参数组合[7-9]。针对该问题，本文构建了基于粒子群优化算法和最小二乘支持向量机的热电偶非线性校正模型。运用改进PSO算法对LSSVM算法中的惩罚系数和核函数参数进行优化求解，以获得最佳的参数组合。将该方法应用于有限空间爆炸实验的温度测量中，能够在一定程度上减小热电偶的非线性误差，提高测量结果精度。

1 方 法

1.1 传感器非线性校正原理

在测量领域中，大多数传感器的输入输出关系均满足如下关系式：

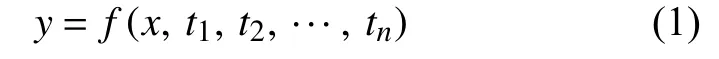
式中：y——传感器输出值；

x——传感器输入值；

t1,t2,···,tn——n个非目标参数。

若t1,t2,···,tn和y均为x的单值函数，则式(1)存在反函数：

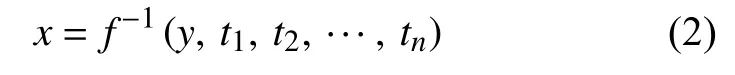
然而反函数多为非线性函数，难以确定其解析式，通常可采用神经网络、支持向量机等校正模型逼近这种非线性函数关系。

设传感器输出为y=f(x,t1,t2,···,tn)，若校正模型可满足

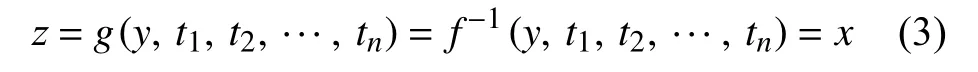
则经校正模型后的传感器输出z与输入量x保持一致，由此可以实现传感器的非线性校正。

1.2 最小二乘支持向量机

最小二乘支持向量机是一种基于统计学习理论的优化方法，它将支持向量机算法中目标函数的约束条件由不等式约束转化为等式约束，将求解二次规划问题转化为求解线性方程组问题，有效降低了算法的复杂程度，在解决非线性优化问题时表现出较强的鲁棒性、泛化能力和大规模运算能力[10-11]。

最小二乘支持向量机算法的基本思想如下：对于给定的训练样本集 {xi,yi}，其中xi为N维输入样本，yi为输出样本。支持向量机是通过非线性变换将N维输入数据从原空间映射到高维特征空间F，并在此空间中构造最优线性回归函数：

式中： ϕ (x)——由原输入空间向高维特征空间的非线性映射；

ω——权值向量；

b——偏置量。

根据结构风险最小化原则，引入松弛因子ei，将式（4）转化为如下最优化问题：

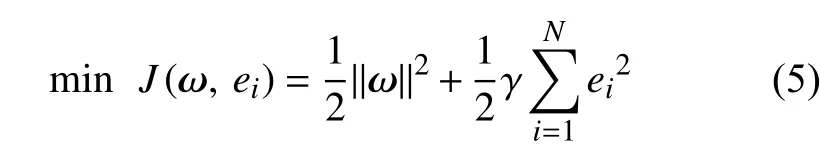
其中，γ为惩罚系数。

上述最优化问题的约束条件为：

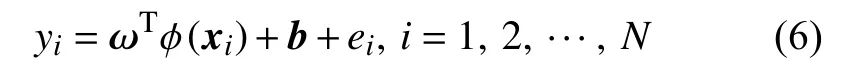
为方便求解，将上述最优化问题转化为其对偶形式，同时建立Lagrange函数如下：

1.3 基于线性递减权重法的改进PSO算法

PSO算法是一种基于群体智能优化理论的并行搜索算法。算法采用基于群体的全局搜索方法和速度-位移模型，有效平衡了搜索过程的方向性和多样性，具有较快的收敛速度和较好的全局搜索能力，适用于非线性问题的优化求解[12-13]。

在PSO算法中，惯性权重是保证算法高效搜索并避免陷入局部最优的关键参数。为使算法获得最佳的搜索结果，本文采用线性递减权重法对PSO算法进行改进，其计算步骤如下：

1）初始化种群中各个粒子的位置和速度：设在D维搜索空间中，种群中粒子个数为m，第i个粒子的位置和速度可分别用D维向量Xi和Vi表示为：

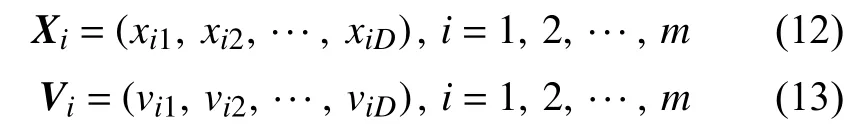
2）评价粒子的适应度，将第i个粒子迄今为止搜索到的最优位置称为个体极值pbest，记作：

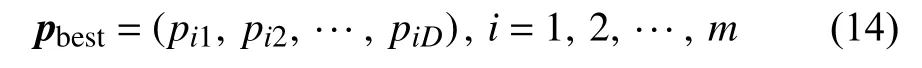
将整个种群迄今为止搜索到的最优位置称为全局极值gbest，记作：()

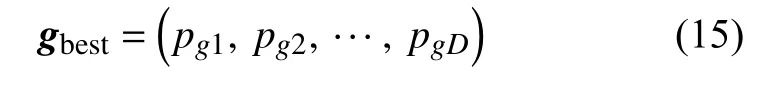
3）按照以下公式更新粒子的速度和位置：

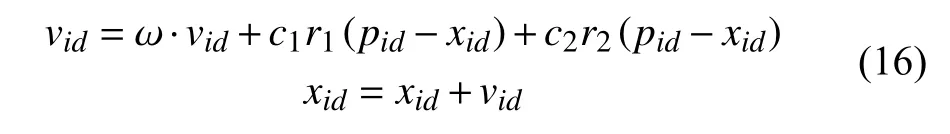
式中：ω——惯性权重；

c1、c2——加速常数；

r1、r2——[0,1]范围内的均匀随机数。

4）根据线性递减权重法，更新惯性权重，其计算公式如下：

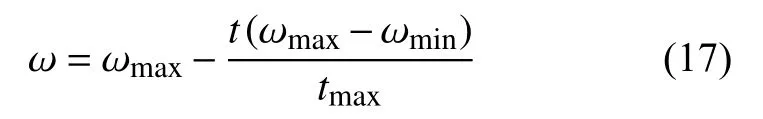
式中：ωmax、ωmin——惯性权重最大值和最小值；

t——当前迭代步数；

tmax——最大迭代步数。

5）将粒子群当前的个体极值和全局极值与历史最佳个体极值和全局极值比较，若当前值小于历史最佳值，则更新pbest和gbest。

6）迭代运算直至算法满足停止条件，停止运行并输出搜索结果，否则返回步骤3）继续运行。

1.4 基于PSO-LSSVM的热电偶非线性校正模型

在LSSVM模型中，惩罚系数 γ和核函数参数σ的选取在很大程度上影响了模型的稳定性和泛化能力。为使LSSVM模型获得最优的非线性校正效果，本文中采用PSO算法对LSSVM模型的惩罚系数γ和核函数参数 σ进行优化，在一定范围内搜索两参数的最优组合。

具体求解流程如下：1）确定模型的训练样本集和测试样本集；2）确定 γ和 σ 的搜索范围，初始化粒子群；3）计算每个粒子的适应度值，确定粒子群个体极值和全局极值，更新各粒子的位置和速度；4）重复迭代至适应度值满足要求；5）将获得的最优参数组合γ 和σ 代入LSSVM模型，运用训练样本集对模型进行训练；6）将测试集的输入样本输入PSO-LSSVM模型，获得模型的输出值，与测试集的输出样本进行比较，分析模型的非线性逼近能力。

2 模型构建与数据分析

以S型热电偶为例，根据有限空间爆炸实验中的温度测量范围和S型热电偶分度表，从1～1 600 ℃之间每隔5 ℃选取一个样本点，以热电势为输入量，以对应的温度值为输出量，组成320个训练样本。待网络模型训练结束后，选取1～1 600 ℃之间去除训练样本后的数据点作为测试样本，以热电势为输入量，输入训练后的网络模型中，比较网络模型的输出温度值和实际温度值，以确定网络模型的拟合精度和泛化能力。

2.1 模型构建

1）BP神经网络模型

设定BP网络的输入层节点数为1，隐含层节点数为30，传递函数选用Tan-Sigmoid函数，训练函数选用trainlm函数，最大迭代次数为10 000，训练精度为0.001，适应度函数为均方误差函数。BP网络模型的拟合误差曲线如图1所示。

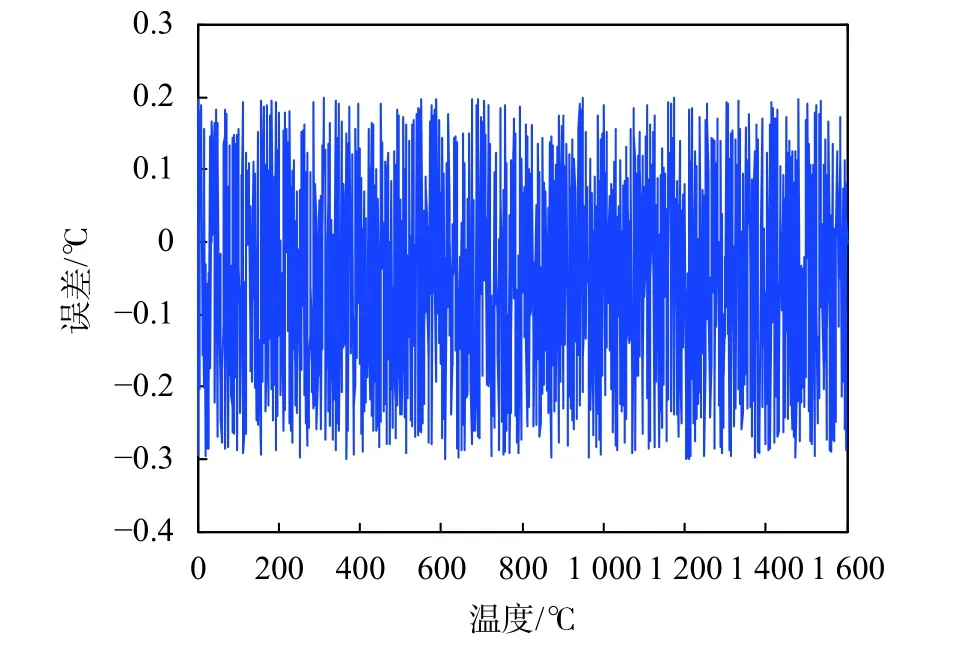
图1 BP网络模型拟合误差曲线

2）RBF神经网络模型

设定RBF网络模型的隐含层节点数为30，训练精度为0.001，训练方法选用梯度下降法，径向基函数选用高斯分布函数，适应度函数选用均方误差函数。RBF网络模型输出的拟合误差曲线如图2所示。

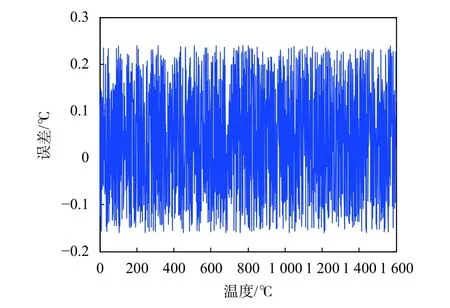
图2 RBF网络模型拟合曲线误差

3）LSSVM 模型

选取惩罚系数 γ为500，核函数参数 σ为0.5，构建LSSVM校正模型，得到该模型的拟合误差曲线如图3所示。

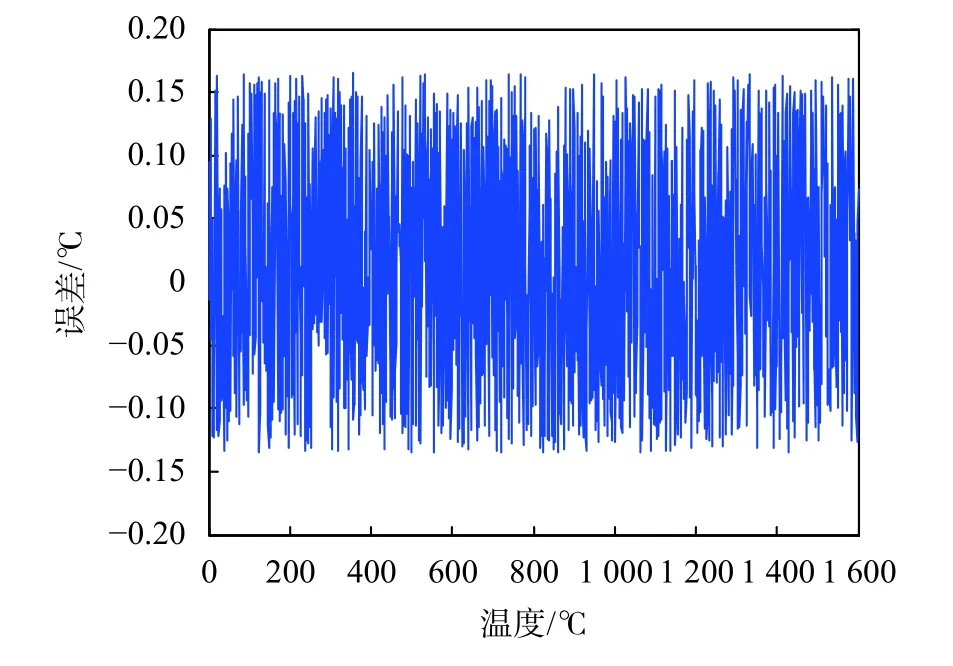
图3 LSSVM模型拟合误差曲线

4）PSO-LSSVM 模型

选取粒子群种数目为30，最大迭代次数为300，学习因子c1为1.5，c2为1.7，惯性权重采用线性递减法由大到小实现递减。惩罚系数 γ的搜索范围设定为[0.1,1 000]，核函数 σ 的搜索范围设定为[0.01,100]，适应度函数选取均方误差函数，经优化得出的LSSVM最优参数组合为：惩罚系数 γ为437.2，核函数参数 σ为0.36。将两参数代入LSSVM模型中，得到该模型的拟合误差曲线如图4所示。

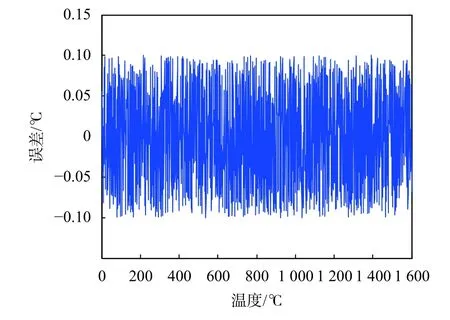
图4 PSO-LSSVM模型拟合误差曲线

2.2 数据分析

为比较上述4种模型的非线性校正效果，选用均方误差Emse和准确率Accuracy来评价其性能优劣，两参数计算公式如下：

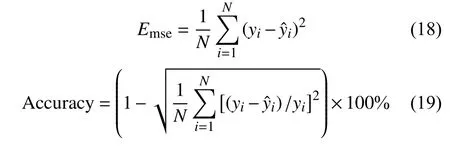
式中：N——测试样本个数；

yi——测试样本期望输出值；

表1给出了4种校正模型的误差区间、均方误差和准确率。由表可知，4种模型的非线性校正性能依次提高，其中PSO-LSSVM模型表现出最优的稳定性和准确性，其最大拟合误差仅为0.12 ℃，均方误差为0.003 3，准确率达到99.82%。

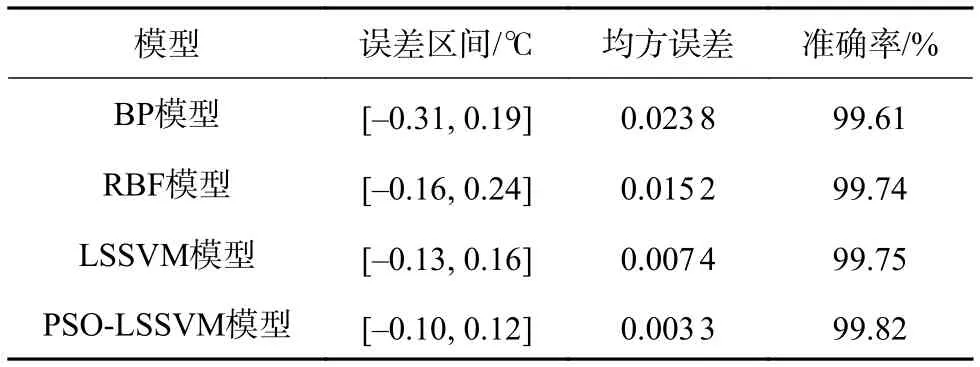
表1 4种模型的非线性校正结果对比

对4种校正模型的收敛速度进行比较，结果如表2所示。由表可知，PSO-LSSVM模型的迭代次数和收敛时间均为最小，具有较快的收敛速度和较高的稳定性。

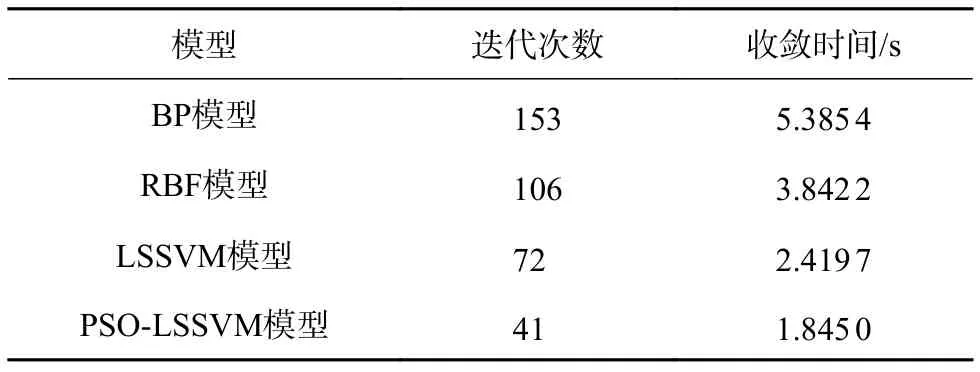
表2 4种模型的收敛速度对比

3 实验验证

在某次有限空间爆炸实验中，在远离爆心的某处安装如图5所示的数据采集系统，包括铠装S型热电偶、信号调理模块、数据采集模块和采集控制主机等。数据采集模块选用Advantech PCI-1710数据采集卡，设定采样频率为1 kHz。

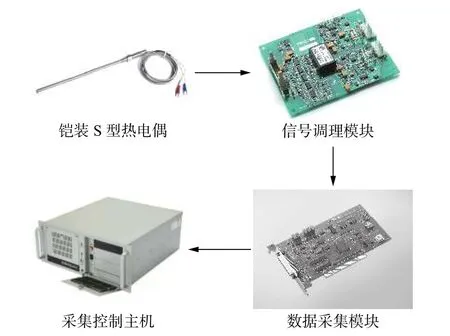
图5 爆炸温度数据采集系统

某次实验中，由上述数据采集系统获得铠装S型热电偶的一组输出电压信号，根据S型热电偶分度表将电压信号转化为温度信号，结果如图6所示。

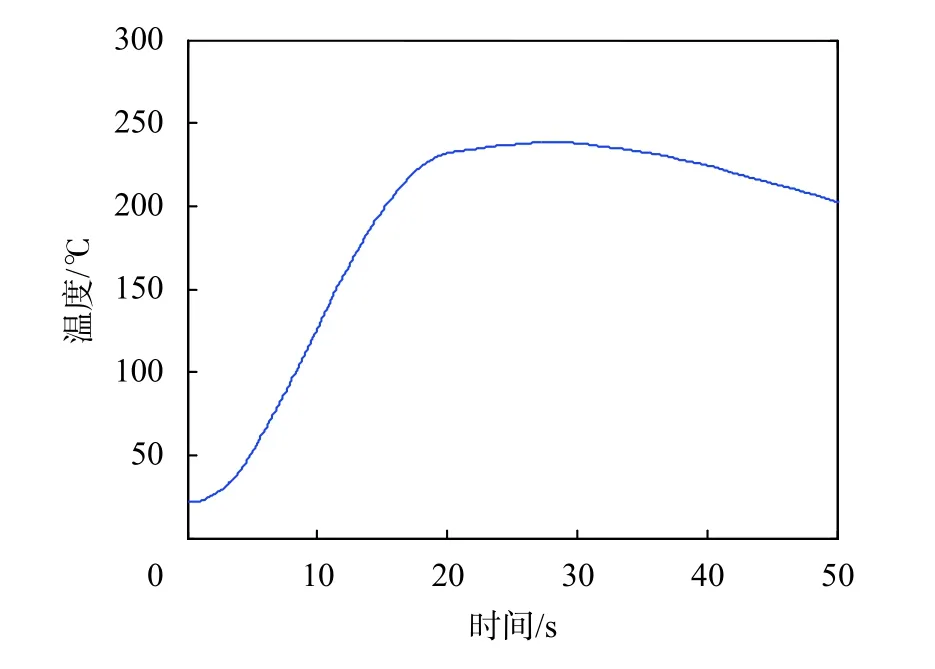
图6 由热电偶分段表转换得到的温度曲线

分别采用上述4种模型将热电偶输出电压信号转化为温度信号，比较由4种校正模型获得的温度值与热电偶分度表之间的误差，结果如图7所示。

图7 4种校正模型非线性误差比较

根据式（18）和式（19）计算4种模型非线性校正结果的均方误差和准确率，结果如表3所示。由表可知，PSO-LSSVM模型表现出最优的非线性校正效果，其最大拟合误差为0.11 ℃，均方误差为0.003 3，准确率为99.86%。

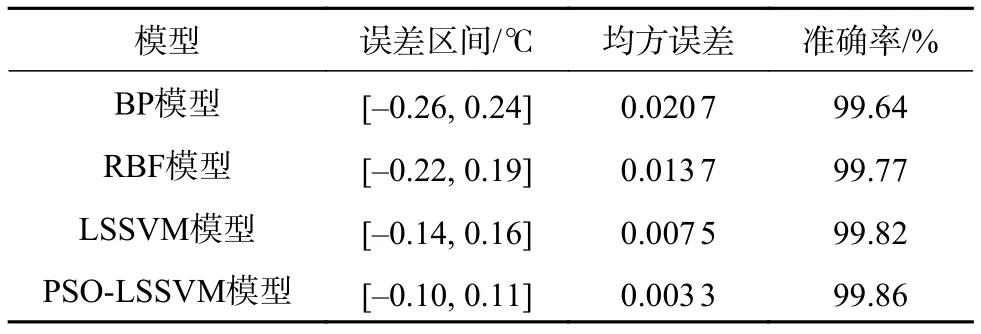
表3 4种模型的非线性校正结果对比

4 结束语

为改善热电偶温度传感器的非线性特性，构建了基于粒子群优化算法和最小二乘支持向量机的热电偶非线性校正模型。针对支持向量机参数难以确定的问题，选用改进PSO算法搜索LSSVM模型中惩罚系数和核函数参数的最优组合，用优化后的PSO-LSSVM校正模型逼近热电偶的非线性函数关系。实验结果表明，该模型在热电偶非线性校正应用中表现出较好的稳定性和准确性。将该方法应用于有限空间爆炸实验的温度测量中，能够在一定程度上减小热电偶的非线性误差，提高测量结果精度。