成形磨砂轮圆弧廓形关键参数在位检测方法及试验研究

师超钰,朱建辉,孙冠男,郭泫洋,王洁浩,包 华

(1. 超硬材料磨具国家重点实验室，河南 郑州 450001; 2. 郑州磨料磨具磨削研究所有限公司，河南 郑州 450001)

0 引 言

近年来，球面、非球面及自由曲面零件在军用和民用产品上的应用越来越广泛。例如轴承、光学镜片、钻头铣刀等精密零件，多为金属、陶瓷、玻璃、硬质合金等典型材料。基于超硬材料（CBN和金刚石）砂轮的超精密磨削技术是保证其加工精度和效率的有效解决手段。

在超精密磨削机床上利用圆弧砂轮将粗毛坯近乎加工到尺寸精度是目前轴承、光学镜片、钻头铣刀等零件的重要精密成形加工手段[1-2]。超精密磨削加工利用磨粒的运动干涉、复印原理获得被加工表面[3]，圆弧形砂轮的轮廓形状误差与加工后工件的面形误差具有一定的映射关系，砂轮圆弧表面的磨粒突出情况影响加工后工件的表面粗糙度以及亚表层损伤深度和密度，修整后砂轮的圆弧轮廓形貌精度决定了工件的加工精度[4-6]。因此，对砂轮形状精度进行精确检测分析，尤其砂轮廓形曲率和圆度的检测，是进行高精度成型零件磨削加工前必须完成的关键工序。

崔长彩基于干涉测量原理实现了金刚石砂轮表面较大范围三维形貌的观测[7]；谢晋采用石墨板复印金刚石砂轮圆弧形轮廓，再用三坐标测量仪检测其形状偏差[8]；顾铁玲基于机器视觉和图像处理算法进行砂轮轮廓测量与磨损状态分析[9]；迟玉伦利用声发射动态监测修整过程中的砂轮廓形[10]；但以上方法均无法直接在位检测出砂轮廓形参数。赵清亮采用点激光测微仪测量圆弧金刚石砂轮表面高度信息，计算出圆弧半径和形状误差[11]；周炼利用点激光传感器实现圆弧金刚石砂轮三维几何形貌的在位检测[12]；但点激光螺旋扫描方式易受砂轮形貌和跳动影响，检测局限性大。

为高效、准确、方便地获得复杂圆弧砂轮关键廓形参数，本文利用线状激光连续扫描砂轮表面形貌，采集形貌位移数据，构建测量矩阵模型，通过数据处理获得砂轮廓形曲率半径、圆度误差关键指标参数，并开展磨削验证试验以及检测不确定度评定[13]，结果表明该方法稳定可靠，检测数据契合磨削结果，可以满足复杂圆弧廓形砂轮工程检测需求。

1 在位检测方法

砂轮廓形测量采用在位检测的方式，即在不拆卸砂轮的情况下方便快捷地完成砂轮的动态在位测量。如图1所示，砂轮在机床上以恒定转速ns旋转，线状激光位移传感器发射线型激光束，激光束平行于砂轮旋转轴中心线，并且激光束辐照方向通过中心线，线型激光位移传感器在砂轮圆周全表面连续扫描采样，采样数据中包含了砂轮表面微观形貌信息，从而完成砂轮表面廓形的非接触式在位测量。

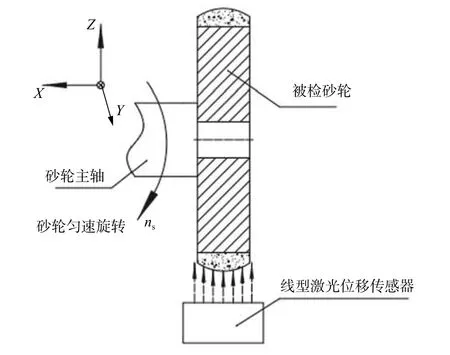
图1 砂轮廓形在位检测方法

对采样数据整周期裁切并去除两端无效数据后，排列组合为矩阵Zm×n，并映射矩阵数据位置信息，构建砂轮表面廓形测量矩阵模型，建立点云坐标系(x，y，z)，数学表述如下式所示：

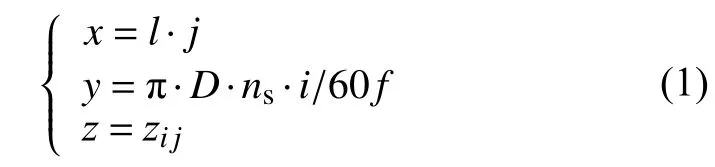
式中：i、j——正整数，且

ns——被检砂轮转速，r/min；

D——砂轮直径，mm；

T——砂轮轴向厚度，mm；

f——激光位移传感器采样频率，Hz；

l——激光束中相邻点间距，mm；

zij——矩阵Zm×n中第i行j列的采样数据值，mm。

在式(1)矩阵模型中增加砂轮圆周信息，变换点云坐标系，数学表述如下式所示：

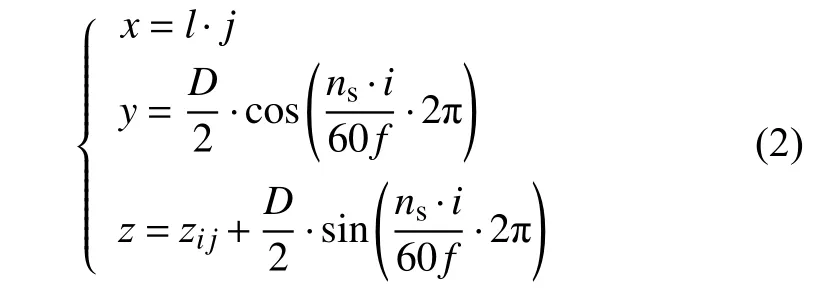
其中各参量表征与式(1)相同。

2 数据处理与分析

针对测量矩阵模型数据进行处理分析，获得砂轮廓形曲率半径、圆弧圆度误差关键指标参数。

2.1 滤波去噪

激光照射在磨粒边缘或交界位置时，传感器会输出奇异噪点，多以极大或极小幅值的形式出现，鉴于数据的三维连续特性，采用双向滑动限幅滤波。即设计滤波窗口在矩阵数据上逐点滑动，窗口数据长度为L，如果窗口极值未超出阈限则窗口数据插入并同位替换寄存数组Z′，如果窗口极值超出阈限则舍弃窗口数据并向数组Z′末位插入空值元素（NaN）。滤波窗口逐行、逐列遍历所有数据点，并将双向滤波结果叠加运算，滤除奇异噪点。滤波算法如下式所示：

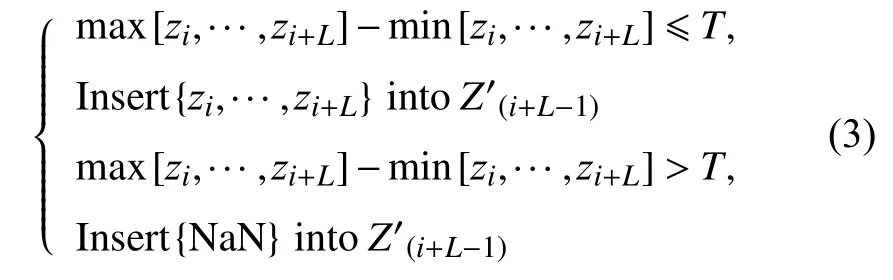
2.2 插值补空

针对滤波后的空值位进行双谐波样条的二维散点插值，重建点云密集规则，还原砂轮三维地貌信息。双谐波样条是一种基于格林函数计算的插值方法，是用中心点位于各观测数据点的多个格林函数进行加权叠加而解析地计算出插值曲面的全局插值方法，特别适合地貌地形的局部变化分析。在三维空间中对N个数据点的受张力p的插值函数 ω (x)满足以下方程：

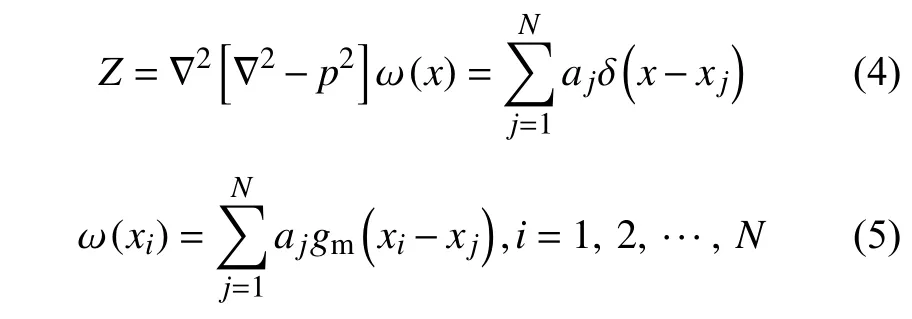
式中： ∇2——拉普拉斯算子；

x——空间位置坐标；

gm——格林函数。

根据方程求解出加权系数aj后就可计算出插值曲面。

2.3 宏观轮廓线提取

为排除砂轮表面微观地貌信息，利用移动平均趋势法针对插值后矩阵数据进行提取砂轮表面宏观轮廓线处理，即取某数据点附近q个数据，按下式计算并将计算值替换该数据点。下式为基于概率统计的均值滤波修正算法，利用算术平均偏差和概率分布评估修正系数，使分布概率高的数据对滤波输出贡献大，分布概率低的数据对滤波输出贡献小，使修正后均值对宏观轮廓变化趋势具有较佳的代表性。矩阵每行数据所有数据点均按此方法计算，并将计算值连成曲线获得砂轮宏观轮廓线。

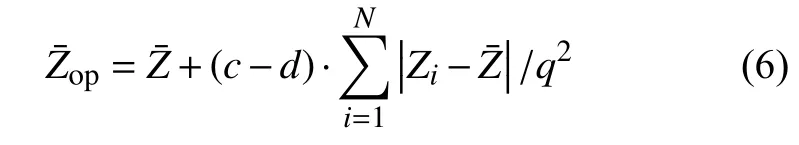
——q个数据点的算术平均值；

Zi——q个数据点的值；

c——q个数据中大于的数据点数；

d——q个数据中小于的数据点数。

2.4 圆弧分段

根据砂轮廓形构成进行圆弧分段处理，方法为：针对一组廓形数据，取一定长度的数据段并逐点滑动，最小二乘线性拟合每个数据段，并将相邻数据段拟合斜率两两比较，如果比较差值的绝对值连续三次超过一定阈值，则判定该区域数据段的中心数据点为不同圆弧特征的分割点。

2.5 非线性曲线拟合

针对圆弧段宏观轮廓线数据进行非线性曲线拟合，以精确评估廓形参数。首先利用下式所示的估计圆参数方程将非线性拟合算法参数初始化，再通过Levenberg-Marquardt算法获得拟合参数集合{R,xos,zos}，该集合是输入数据点的最佳拟合，以最小化观测值与最佳非线性拟合之间的加权均方误差。

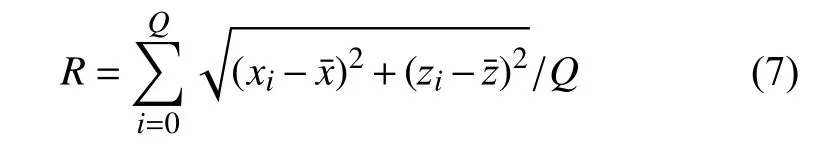
式中：——圆弧段轮廓线数据的算术平均值；

——对应坐标的算术平均值；

Q——圆弧段数据的个数；

R——圆参数估计值。

为避免奇异Hessian矩阵的弱点，Levenberg-Marquardt算法为Hessian矩阵添加正定对角矩阵，提升优化效率和精度。

2.6 参数计算

根据各组拟合结果计算砂轮廓形关键指标参数，如以下式所示：

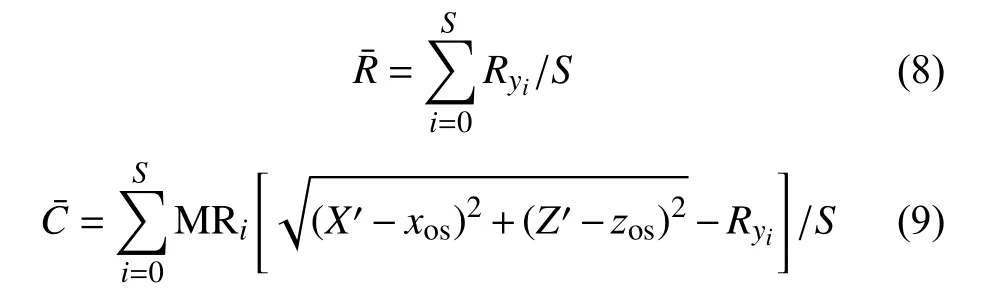
式中：——砂轮廓形圆弧曲率半径；

Ryi——第i行数据对应圆弧段的拟合半径；

S——行数；

——砂轮廓形圆度误差；

MR——极差值；

X′——第i行宏观轮廓线数据对应圆弧段的X位置坐标数组；

Z′——第i行宏观轮廓线数据对应圆弧段的Z值数组；

xos——拟合圆弧圆心X位置坐标；

zos——拟合圆弧圆心Z值。

3 砂轮廓形检测与成形磨削试验结果分析

在CNC8325数控磨床上利用金刚石滚轮插补修整陶瓷CBN砂轮。试验中修整砂轮单段圆弧廓形，设定插补修整圆弧曲率半径15 mm，采用线型激光位移传感器LJ-V7060进行廓形检测。陶瓷CBN砂轮粒度80/100#，外径φ450 mm，宽度16 mm。传感器主要性能参数和测量参数分别如表1和表2所示。

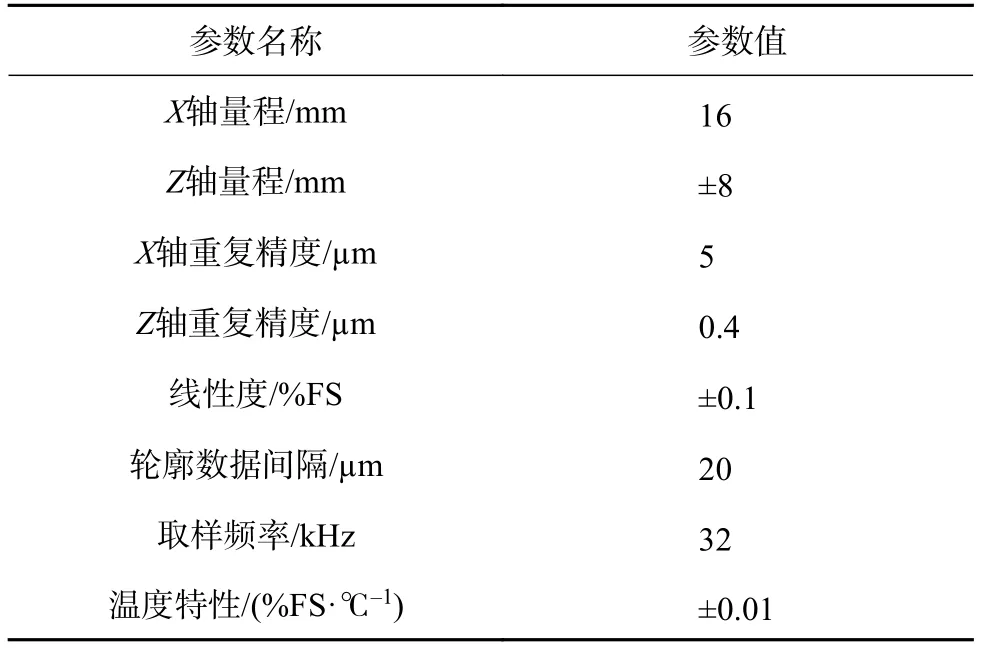
表1 传感器主要性能参数

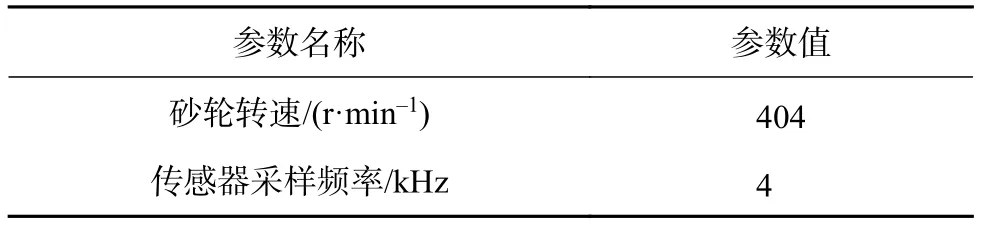
表2 砂轮廓形测量参数

试验中通过高精导轨支架调节激光位移传感器与砂轮的上下向位置，通过机床进给调节传感器与砂轮的前后、左右向位置，支架与机床安装位置高精度配合，以达到“激光束辐照方向平行并通过砂轮旋转轴中心线”的要求。精度满足要求的支架对测量数据影响极小，文中不再讨论。

将测量到的原始数据进行处理，原始数据以及滤波、插值后效果对比如图2所示，图2中各直角坐标系显示范围一致。可见，原始采样数据中存在较多尖峰奇异点和少量无效空值点，边缘锯齿分明；滤波插值后，尖峰奇异点被滤除，且正常数据无失真，可真实反映砂轮表面三维地貌。

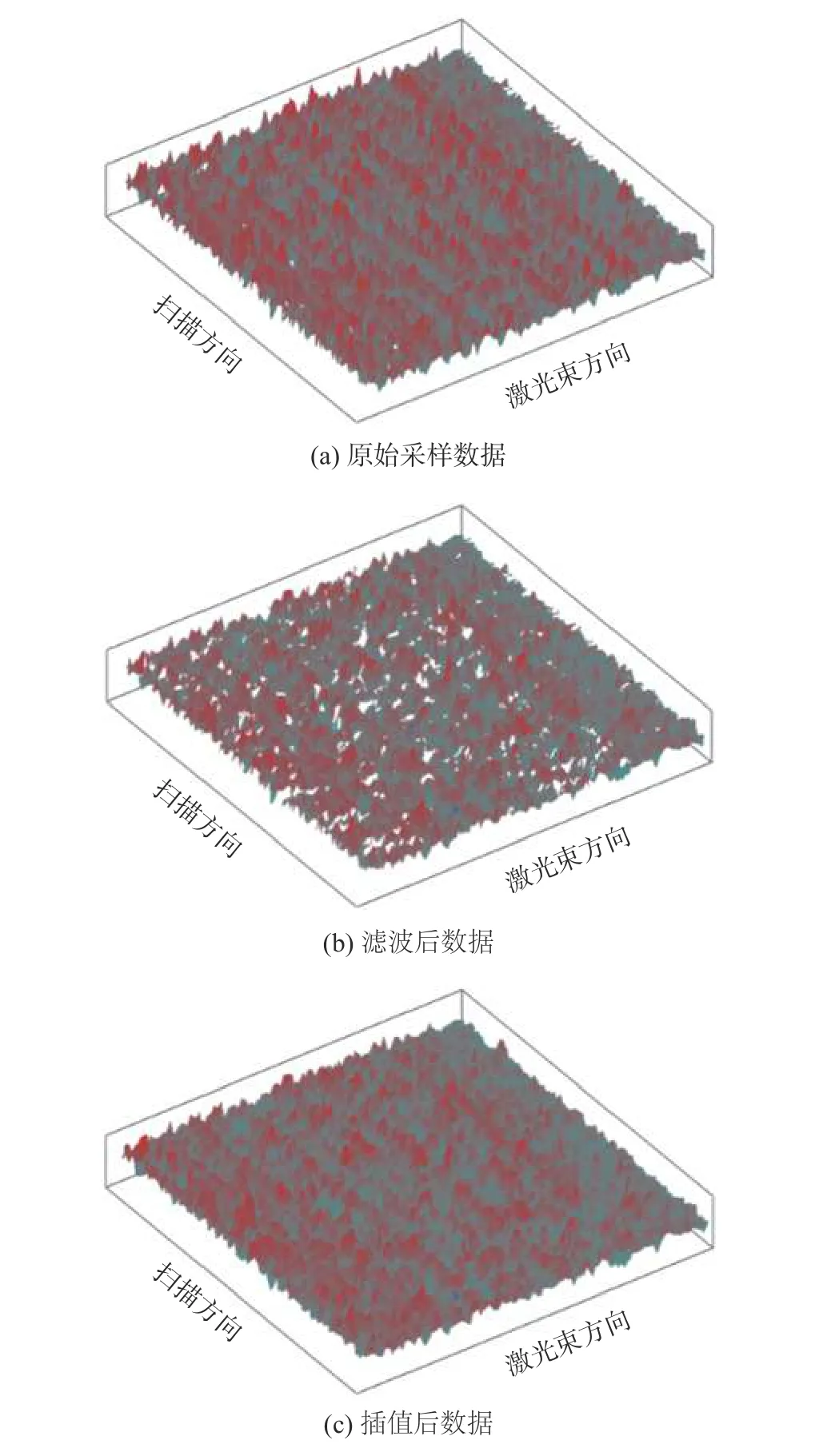
图2 滤波、插值数据处理效果

针对滤波、插值后的数据进行处理分析，由测量矩阵模型生成砂轮三维几何形貌如图3所示。某一相位轴截面轮廓采集数据及其拟合廓形曲线如图4所示。以所有相位的拟合廓形曲线构建砂轮圆周全表面标准三维廓形，并与轮廓采集数据作差，得砂轮表面廓形数据的偏差分布，如图5所示，可见绝大部分采集数据与标准廓形偏差较小，拟合廓形曲线可真实反映砂轮表面圆弧廓形。

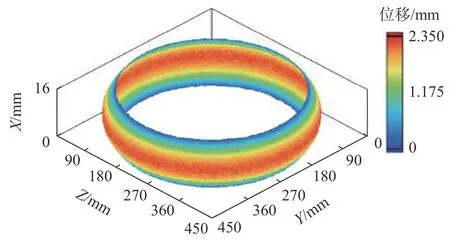
图3 砂轮表面三维几何形貌

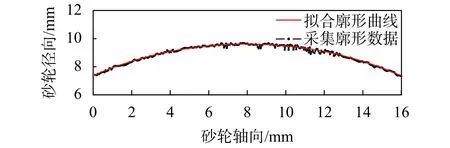
图4 砂轮轮廓数据及拟合曲线

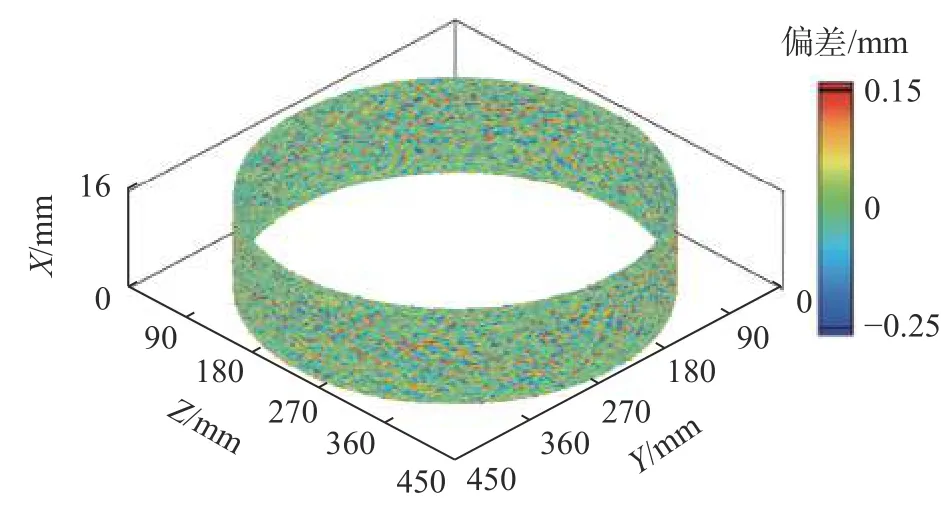
图5 砂轮表面廓形采集数据偏差分布

计算不同相位处轴截面轮廓的圆弧曲率半径和圆度误差以及相应的圆心坐标，得平均圆弧半径为15.002 mm，平均圆度误差为3.7 µm。不同相位处圆弧的曲率半径分布如图6所示，不同相位的半径波动极差为0.081 mm，波动率0.54%。不同相位处的圆弧圆度误差分布如图7所示，最大圆度误差为5 µm，经过宏观轮廓线提取处理，圆弧圆度误差计算可有效避免砂轮表面粗糙形貌影响。

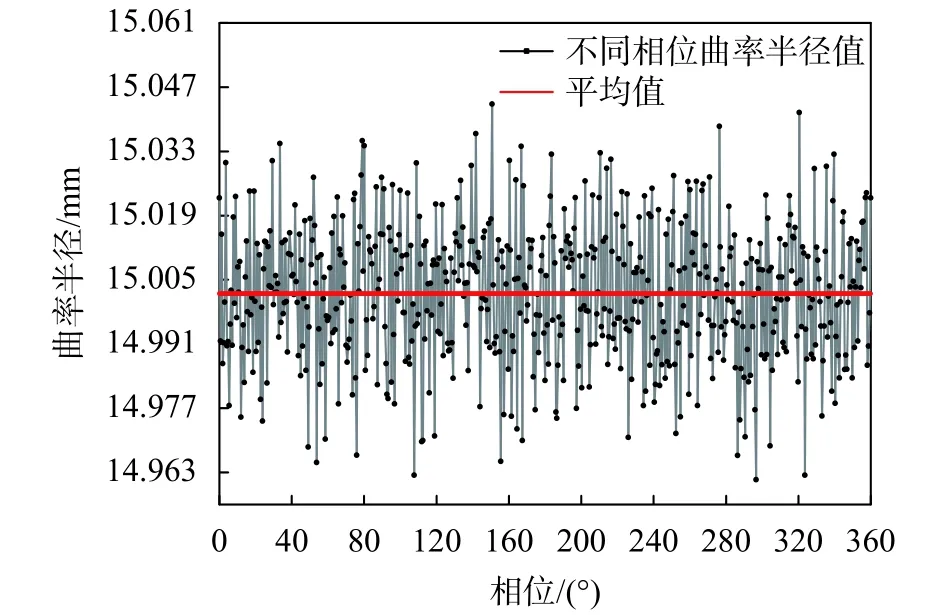
图6 砂轮不同相位圆弧廓形曲率半径

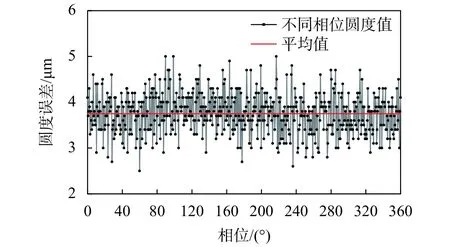
图7 砂轮不同相位圆弧廓形圆度误差

为验证本文提出的砂轮廓形在位检测方法及结果是否满足磨削检测要求，采用上述已检砂轮在CNC8325磨床上开展GCr15材料工件的切入精磨试验，工件直径φ60 mm，磨削工艺参数如表3所示。由于在工件槽形基础上开展的精磨余量仅0.3 mm，而且CBN砂轮具备极高耐磨性，因此磨削中砂轮损耗可忽略不计。

表3 磨削工艺参数

磨削后利用HOMMEL轮廓仪T8000C在工件表面等间隔（30°）相位测量12次，测量结果如图8所示，工件磨削表面全部检测相位处廓形圆弧平均曲率半径15.004 mm，极差0.009 mm，廓形平均圆度误差2.3 µm，最大圆度误差3.8 µm。根据轮廓仪原始采集数据生成的磨削工件表面三维廓形如图9所示。

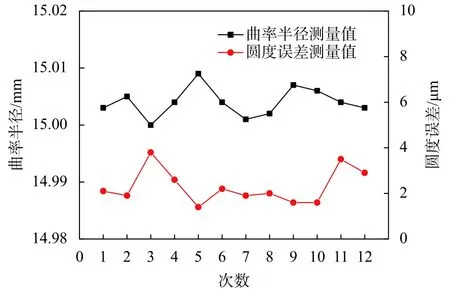
图8 工件沟道圆弧半径检测结果

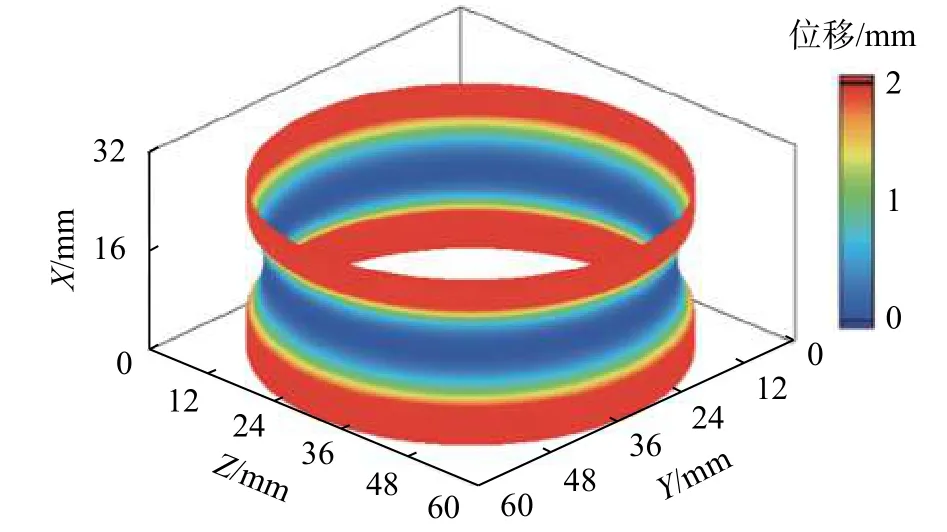
图9 磨削工件表面三维廓形

在充分考虑砂轮和工件表面特性以及检测样本容量的差异后可知，磨削工件廓形与砂轮廓形检测结果表现出较高一致性，本文提出的砂轮廓形在位检测方法可以摆脱“试磨法”局限，反映砂轮成形磨削精度，发挥出较好的工程应用价值。

4 廓形参数检测结果可信度分析与讨论

由于测量误差的存在，任何测量过程均不可能得到真值结果，但存在一个区间，使测量的真值以一定置信概率分散于该区间范围内，这个区间就是测量扩展不确定度。评定测量不确定度可反映检测结果的质量水平及可信赖程度。

鉴于砂轮廓形在位检测时的随机变化不确定因素多、数据运算复杂、环境条件影响大，将基于贝叶斯信息融合的不确定度评定方法应用于试验测量情形，能够充分融合历史先验信息和当前样本信息，具有更合理、可靠的评定效果。

廓形参数检测结果取数据均值，已有反映测量均值 µ信息的先验分布和当前测量样本X=(x1,x2,···,xn)后，可利用下式进行建模：

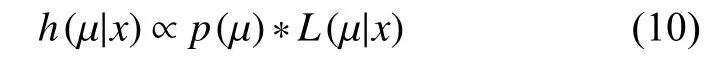
其中h(µ|x)为后验分布密度函数,p(µ)为先验分布密度函数,L(µ|x)为当前测量样本的似然函数。根据评定模型计算后验分布的期望作为测量结果最佳估计值，标准差作为标准不确定度。

实际检测中发现，廓形参数检测结果符合正态分布，可利用贝叶斯共轭分布理论将前一次的后验分布作为下次计算的先验分布，实现检测结果的多级评定和持续更新。

通过本文提供的检测方法针对上述试验砂轮在不同的时间段、不同的室温条件下，由不同的操作人员先后重复检测3组样本，每组样本检测10次，结果如表4所示。其中，单次曲率半径和圆度误差检测结果为砂轮所有相位处轴截面采样数据处理结果的均值。

表4 廓形参数检测结果

以曲率半径的评定为例，先将第一组数据作为先验信息，第二组数据为当前样本信息，计算先验均值 µ0=15.003 mm，先验标准差 σ0=2.8 µm，样本均值1=15.007 mm，样本标准差τ1=1.3 µm。测量数据服从正态分布，则先验分布密度函数为：

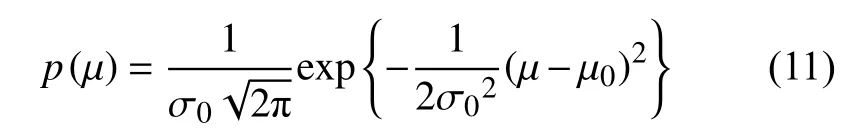
当前样本 的似然函数 为：

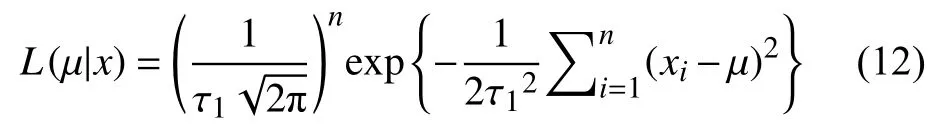
由于后验分布也是正态分布，将式(11)和(12)代入式(10)可得后验分布：

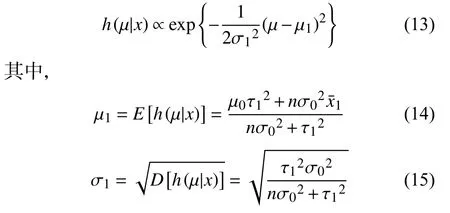
利用式(14)和(15)计算得 ,µ1=15.006 mm，σ1=0.4 µm。再将第一、二组数据信息融合后的后验分布作为先验信息，即 µ1为先验均值,σ1为先验标准差，第三组数据为当前样本信息，样本均值2=15.002 mm，样本标准差 τ2=1.4 µm，同法计算出后验分布的期望µ2=15.004 mm，标准差σ2=0.3 µm。所以，融合三组检测数据的砂轮廓形曲率半径最佳估计值ϵ= µ2=15.004 mm，A类标准不确定度uA(x)=0.3 µm。

根据表1中激光位移传感器的线性度和重复精度参数，以传感器自身温漂10 ℃计，则线性度引入的测量值最大误差为±8 µm；Z轴重复精度引入最大误差为±0.2 µm；X轴重复精度对Z测量值的影响在圆弧廓形两端最大，小于±2.5 µm，在圆弧中间最小，接近0，所以X轴重复精度引入最大误差为±2.5 µm。综合以上误差值，传感器自身特性引入的测量最大误差小于±10.7 µm，取误差均匀分布下置信水平为1时的置信系数，则传感器自身引入的不确定度分量。

外部环境影响可排除气压、粉尘、振动等因素，主要分析温度变化。认定检测环境温度变化范围小于10 ℃，根据表1中激光位移传感器的温度特性计算环境温度引入最大测量误差小于±8 µm，同样取均匀分布的置信系数则环境引入的不确定度分量。

由上可得，在置信概率95%的条件下，砂轮廓形圆弧曲率半径的检测结果可表示为：(15.004±0.015) mm，即检测真值不超出±0.015 mm区间范围的概率为95%，置信区间范围占比最佳估计值0.2%。

同样的，针对砂轮廓形圆弧圆度误差开展不确定度评定，得在置信概率95%的条件下，砂轮廓形圆弧圆度误差的检测结果可表示为：(3.62±0.22) µm。由于砂轮表面粗糙形貌影响，砂轮廓形圆度误差要大于工件圆度误差。

综上可见，本文提出的砂轮廓形在位检测方法获得的评估值以较高的置信概率收敛在较小的置信区间内，检测结果稳定可靠，满足工程实际需求。

5 结束语

本文采用线状激光连续扫描测位移的方式采集砂轮表面形貌数据，并构建三维廓形测量矩阵模型，通过滤波去噪、宏观轮廓线提取、非线性曲线拟合等数据处理算法计算出砂轮廓形曲率半径、圆度误差关键指标参数，实现了砂轮廓形的非接触式在位检测。

利用本文提出的廓形在位检测方法，针对某陶瓷CBN砂轮开展检测和磨削试验，试验结果表明，砂轮廓形检测结果与磨削工件廓形具有较高一致性，砂轮廓形检测结果可以准确反映工件加工精度。验证了该方法的可行性，在高精度成型零件磨削加工领域具有较好的工程应用价值。

针对同一陶瓷CBN砂轮开展检测不确定度评定，评定结果显示，置信概率95%的条件下，砂轮廓形曲率半径的置信区间为±0.015 mm；廓形圆度误差的置信区间为±0.22 µm。验证了该方法检测结果的可信度，可满足成形磨圆弧砂轮廓形参数高精度检测需求。