无穷级数求和教学中思政案例设计

罗 琳

(上海第二工业大学 文理学部,上海201209)

0 引言

高等数学是大学数学的核心课程, 是许多专业后续课程的重要学习基础,也是许多专业技术的重要知识工具[1]。学习高等数学如何在人才培养质量的提升中发挥积极作用是高校数学工作者需要研究和实践的问题。随着教育改革不断深入, 许多数学工作者正在探讨教学改革的有效措施,如提出分层教学、引进数学软件辅助教学、线上线下混合式教学等措施[2-7], 这些都在某种意义上丰富了高等数学的教学方法,大大满足了大学生个性化学习需求。

党的十八大以来,习近平总书记站在国家繁荣、民族振兴、教育发展的战略高度,多次就高校落实立德树人根本任务做出重要指示并强调 “要把立德树人内化到大学建设和管理各领域、各方面、各环节,做到以树人为核心,以立德为根本” 。近日,教育部在《高等学校课程思政建设指导纲要》中指出,全面推进高校课程思政建设是深入贯彻习近平总书记关于教育的重要论述和全国教育大会精神、落实立德树人根本任务的战略举措,高校要深化教育教学改革,充分挖掘各类课程思想政治资源,发挥好每门课程的育人作用,全面提高人才培养质量。

高等数学作为大一新生的核心课程,有责任率先履行好立德树人的根本任务,将思政教育引入到课堂教学中,不知不觉培养学生社会主义核心价值观, 正如习总书记说的 “扣好人生第一粒扣子” 。为此,高等数学课堂教学中恰当引入思政元素,潜移默化培养学生以树人为核心, 以立德为根本, 把个人价值和社会责任结合起来,培养学生的创新精神和使命担当。近年来, 一些学者正在开展这方面的研究工作,探讨课程思政在人才培养中的示范引领作用[8-11]。如姜爱国等[9]通过引入思政元素提高课堂教学的感染力,发挥育人功能。俞能福等[10]提出挖掘高等数学文化内涵,践行课程思政,培养学生的科学精神和使命感。褚小婧[11]提出选择合适的数学教学内容以恰当的方式呈现课程思政,以达到立德树人的目的。本文以高等数学中无穷级数求和作为教学案例,探讨如何根据教学内容恰当引入思政元素,在教学中培养学生的创新精神和使命担当,发挥课堂教学这一主渠道的作用。

1 无穷级数求和知识内容

无穷级数是高等数学课程的一个重要的知识点, 它是表示函数、研究函数以及数值计算的一种有效工具。历史上, 无穷级数的求和问题曾经困扰数学家长达几个世纪。有时一个无穷级数的和是一个数、一个函数、一个无穷大; 有时一个无穷级数的和没有确定的结果。19 世纪上半叶, 法国数学家柯西建立了严密的无穷级数理论, 使得无穷级数成为一个强有力的数学工具。例如,能把许多可微函数表示成无穷多项式, 如:sinx=-∞ ＜ x ＜+∞;ln(1 +x) =-1＜x≤1。并在误差范围内把它截断成有限多项式,这些无穷多项式不仅提供了可微函数的有效多项式逼近,而且有许多实际应用。

如果一个无穷级数是收敛的,那么级数求和的思想,体现的是从无穷到有限的过程。在教学过程中,首先要从直观上指导学生明白: 研究无穷级数貌似复杂(因为有无穷项相加), 但实际上是希望将无穷个函数的和或者无穷个数的和通过一个具体的函数或者数去表达。当然这一过程要求这个无穷级数满足某些条件或者数学上具备某些性质才行。无穷级数和的概念如下:

从这个定义不难看出,如果无穷级数的部分和数列收敛, 那么这个无穷级数的和就一定存在。在计算一个无穷级数的和时可以直接应用这一定义求解。但能够直接应用定义求解的问题毕竟不多, 尤其是当级数通项稍微复杂的时候,更是需要我们利用级数的相关性质来解决,如幂级数和函数的连续性、逐项积分、逐项求导等性质。

2 数项级数求和思政元素切入

问题1计算下列级数的和。

解题过程:

(1)直接法。由于

所以

(2)间接法。由于

(3)间接法。根据上题的启发,有:

思政元素切入:

第(1)题采用直接法,即直接利用级数收敛的定义求和。而第(2)、(3)题采用间接法,也就是利用了指数函数的泰勒展开式进行间接求和。两种解法充分体现了直接法与间接法间相辅相成、相得益彰的美好效果,从而指导学生在工作和生活中也要做到发挥所长、相互配合、相互补台,才能彼此促进、彼此成就。例如, 在大众创业、万众创新的伟大浪潮中, 许多大学生毕业后希望自己创业。但一个创业公司,想要快速成长起来,需要学会利用已有的技术和平台, 解决自身企业产品的难题。众所周知的小米科技公司成立于2010年,至今已走过10年创业之路,从最初10 人左右的小公司到如今世界知名的全球化移动互联网企业。正如公司CEO 雷军在小米10 周年庆典上的分享:在公司起步阶段,没有自己的手机做研发,就先在别人家的手机上做;操作系统复杂,先找一套开源系统,在开源系统的基础上研发。正是利用了这些已有的技术平台, 才有了小米公司从零开始乘风破浪、硕果累累的十年。通过这样具体的实例引导学生学会不怕困难、解决困难的方法,培养他们的创新创业精神。

3 函数项级数求和思政元素切入

问题2求下列级数的和。

解题过程:

(1)收敛域为-1 ≤x≤1。

设s(x) =, 则s(0) = 0, 且x·s(x)=。

则当0＜|x|＜1 时,两边求导2 次得：[x·s(x)]′=⇒[x·s(x)]′′=

两边积分2 次得:x·s(x)=x+(1-x)ln(1-x)。所以

由于幂级数在x=±1 处收敛,那么其和函数分别在x= 1,x=-1 处分别左、右连续,即=1。因此其和函数为:

该结论可应用于问题1 中的第(1)题(只要选择x=1 即可)。

(2)收敛域为-1＜x ＜1。

设s(x)=(n+1)2xn,则两边积分得

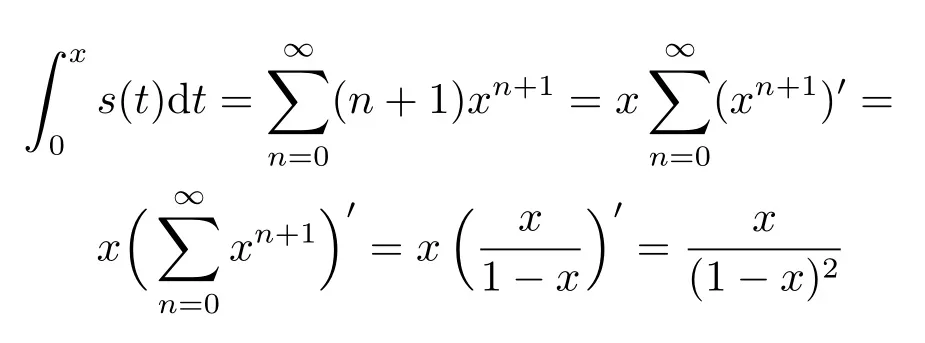
两边求导,即得所求和函数为:s(x) =(-1＜x ＜1)。

(3)收敛域为-∞＜x ＜+∞。

设s(x)=,则两边积分得

两边求导, 即得所求和函数为:s(x) =-∞＜x ＜+∞。

该结论可应用于问题1 中的第(3)题(只要选择x=1 即可)。

思政元素切入:

函数项级数求和本身是个困难的知识点。以上两个小题均为函数项级数中幂级数求和的典型问题。从这两问题的解答过程不难看出,求幂级数的和函数离不开求导和积分的步骤。第(1)题利用先求导再积分的过程来求解,第(2)、(3)题利用先积分再求导的过程来求解,其目的都是为了去掉多项式的系数, 实现等比级数求和目标。从解决问题的步骤来看,无论是先求导再积分还是先积分再求导,都是为了实现算法变换的平衡。从这个问题的解法可以很自然地指导学生:科学计算需要平衡,生活需要平衡, 大自然更需要平衡。随着现代社会的飞速发展,人类获得了很好的物质享受,但往往忽视了自然界的平衡。如:热带雨林遭受破坏、户外动物被肆意猎杀等, 这些行为都是破坏大自然平衡的现象。这次新冠肺炎疫情也是人类破坏大自然平衡所遭受的惨痛教训。通过这些实际事例, 指导学生充分认识到大自然就是人类赖以生存的家园,我们需要维护这个家园的平衡,以健康的方式共建和谐美好平衡的自然环境。这一思政元素引入的过程, 不仅训练了学生的科学思维,也进行了科学伦理的教育,从而培养了学生探索未知、追求真理、勇攀科学高峰的责任感和使命感。

4 结语

级数求和是高等数学的一个重要知识,教师在教学过程中通过精心设计,根据教学内容非常自然地在讲解知识的过程中引进课程思政,既传授了级数求和的科学知识,也通过思政元素的切入,润物细无声地引导学生培养立德树人的思想。正如前文在问题1 的讲解过程中通过解题方法,教会学生如何有效利用直接法或间接法去解决问题,在问题2 的解答过程中指导学生如何在计算过程中实现变换平衡的思想。这些思政元素的自然切入, 不仅丰富了课堂,提高了趣味性和快乐感,更重要的是培养了学生思考问题的方式、不怕苦难的信心、解决问题的方法以及创新能力的提升。而且从教学问题中拓展出来的实际事例潜移默化地培养了学生的使命感和担当意识,从而培养学生爱国、爱家、爱环境的责任担当。

习近平总书记在北京大学师生座谈会上强调 “教育兴则国家兴、教育强则国家强。高等教育是一个国家发展水平和发展潜力的重要标志” 。作为教书育人的实践者,让我们不懈努力,开拓进取,在教学中履行立德树人的根本任务,培养具有使命感和担当精神的创新型人才,为中华民族伟大复兴的灿烂前景奠定坚实基础。