基于逆Gamma分布的变分自适应滤波算法

戴 卿，许辉熙，马云峰

(1.西南交通大学 地球科学与环境工程学院，成都 610031；2.四川建筑职业技术学院 博士后创新实践基地，四川 德阳 618000；3. 重庆水利电力职业技术学院 建筑工程系，重庆 402100)

0 引言

以GNSS(Global Navigation Satellite System，全球导航卫星系统)/SINS(Strapdown Inertial Navigation System，捷联惯导系统)紧耦合系统为研究热点的现代导航技术，因其具有灵活性大和动态导航定位精度高的特点，近年来受到越来越多测量学家的关注。然而导航系统在实际工作中受卫星可见性和外界干扰等因素影响，量测噪声随机模型的统计特性随观测条件会发生改变，如不加以考虑就会引起系统稳定性和精度的降低[1]。为此，利用函数模型和随机模型作为补偿手段的自适应滤波理论相继被提出[2]。Sage-Husa滤波能够实时获取当前历元量测噪声的统计特性，但该方法要求各历元量测信息同类、同维、同分布，且当运动载体产生大的扰动时，会影响估计效果[3]。渐消滤波通过引入一个渐消因子使滤波算法符合最优估计条件，但这种方法只能用于时变过程噪声，不能处理量测噪声[4]。抗差自适应滤波可用于量测噪声发生扰动或异常的情况，通过调整自适应因子和等价权矩阵因子达到稳定状态估值的目的，但该算法需要有冗余的量测值[5]。为更好地解决滤波中量测噪声协方差未知或不准确的问题，有学者提出包含量测噪声的最优Bayesian滤波，但该算法在实际应用中却面临被积函数复杂、变量维数高的问题，且噪声方差阵的引入使求解更加困难，从而影响其推广使用[6]。研究人员基于机器学习的思想提出了变分Bayesian学习(Variational Bayesian, VB)，即通过近似的方法求得次优解，以较少的运算量进行较高精度的参数估计，解决Bayesian估计在实际应用中被积函数计算复杂的问题，具有收敛速度快的特点，适应于高维观测环境，可有效提升估计速度[7]。变分Bayesian学习在随机系统参数估计、盲源分离、语音识别和独立成分分析等领域取得了一定的应用和进展[8]。

受上述研究工作启发，本文考虑GNSS/SINS紧耦合组合导航系统中卫星量测噪声的时变特性，对滤波随机模型做进一步精化处理，在变分Bayesian理论框架下提出了一种基于逆Gamma分布的变分自适应滤波算法，利用变分Bayesian理论来解决量测噪声协方差未知或不准确时的参数自适应估计问题，并通过数据测试验证了该算法的鲁棒性、实时性和准确性，为其今后在组合导航系统及其扩展应用提供了一定的理论支持。

1 问题描述

最优Bayesian滤波框架推导的卡尔曼滤波，需要以系统模型准确已知为前提条件。当过程噪声已知，量测噪声未知时，可导出时刻包含量测噪声的最优Baysian滤波形式为

p(xk,Rk|xk-1,Rk-1)=p(xk|xk-1)p(Rk|Rk-1) (1)

式中：p(·)代表似然概率；x为状态量；R为量测噪声方差。设量测量Yk-1={y1,y2，…,yk-1}，由此得到时间更新方程为

量测更新方程分别为

式(1)～(3)构成了量测噪声方差未知的最优Bayesian滤波过程。分析发现上述计算中存在多维数值积分的问题，且量测噪声方差的引入使得式(1)～(3)难以获得解析解。

2 基于逆Gamma分布的变分自适应滤波

2.1 算法原理

当量测噪声难以准确描述时，可用逆Gamma分布(Inverse Gamma, IG)来模拟协方差，并进行近似求解[9]。为此，将式(2)中的量测噪声通过逆Gamma分布近似

由于式(3)中p(yk|xk,Rk)噪声方差与量测噪声具有相关性，难以获得解析形式，故将其改写为

p(xk,Rk|Yk)≈Qx(xk)QR(Rk) (5)

并用KL(Kullback-Leibler)散度进行度量，得

将上式分别对Qx(xk)和QR(Rk)求最小极值

进一步求得量测更新方程

假设存在线性化模型

xk=Fk-1xk-1+wk-1(10)

yk=Hkxk+vk(11)

式中：Fk-1为状态转移阵；wk-1为过程噪声；Hk-1为量测矩阵；vk-1为量测噪声。

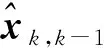
式中：i=1,2,…,l，l为量测方差维数；p∈(0,1]为预测加权系数，p=1时，噪声方差为固定值，p越小方差参数和α与β前一时刻值的关系越弱。

上式中νi难以从量测量中求得，故根据式(11)得到k时刻的量测噪声精确表达式为

vk=yk-Hkxk(14)

式(14)说明vk与xk有关，但xk只能由卡尔曼滤波的中间变量近似得到。

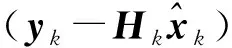
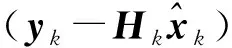
综上，得到基于逆Gamma分布的自适应卡尔曼滤波递推过程，即

时间更新阶段

参数迭代更新

量测更新阶

式中：为量测噪声方差阵的估值；αk=[αk,1,αk,2,…,αk,l]T；βk=[βk,1,βk,2,…,βk,l]T；ρ=[ρ1,ρ2,…,ρl]T。计算迭代次数≤3次。

2.2 性能分析

借鉴文献[5]中基于残差的自适应估计(Residual Adaptive Estimation, RAE)算法，量测噪声方差估计采用下式表述

式中，N=k-i0+1为残差序列总数。与本文基于逆Gamma分布的算法相比较，两种算法的自适应调整均依赖于残差序列和量测协方差阵，但本文讨论的算法避免了RAE算法中滑动窗中新息序列存储及求和运算，其k时刻估值仅与k-1时刻有关，易于迭代实现。另一方面，基于逆Gamma分布的算法在噪声方差估计中只求解对角元素，并利用ρ实现对独立变化噪声的跟踪调节，较RAE算法更为灵活。因此，两种算法在估计精度上接近，但在实用性上本文所研究的优化算法更有优势。

3 数据测试

为验证算法有效性，本文采用MATLAB R2014a 编写的GNSS/SINS紧耦合仿真平台进行数据测试。设置部分仿真参数如下：运动载体初始位置经度为125°，纬度为50°，高度为300 m；初始失准角为5°5′20″；陀螺仪零偏为20°/h，随机游走为0.07°/(h·Hz1/2)；加速度计零偏为50 mg，随机游走为6 mg/(h·Hz1/2)；机动时间为1000 s；仿真可见卫星为5颗。借鉴文献[5]的思路，虽然实际观测中每颗卫星受到的干扰程度不同，但受制于相同无线电信号下量测噪声方差变化趋势相同，因此为考察算法对卫星量测噪声方差变化的跟踪能力，对PRN-8号卫星伪距的量测噪声在600 s至700 s设置了协方差剧烈变动，如图1所示。采用如下两种不同算法方案进行性能验证：

方案1：基于残差的自适应估计滤波算法；

方案2：基于逆Gamma分布的变分自适应滤波算法。

图1～图4所示为数据测试结果。当量测噪声协方差估计不准确或噪声方差发生突变时，图1中方案1和方案2的自适应估计策略均能较好的跟踪方差变化。图2～图4所示两方案滤波结果仍能保持收敛状态。由此说明，方案1和方案2能有效辨识噪声变化并加以利用，维持滤波的稳定性和鲁棒性。

图1 PRN-8伪距噪声方差估计

图2 姿态误差曲线

图3 速度误差曲线

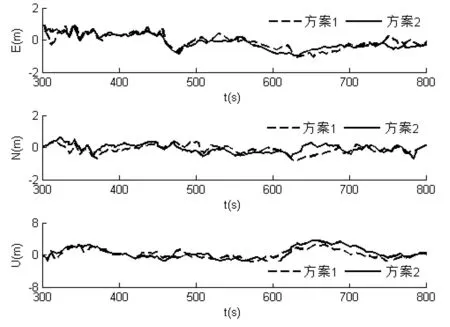
图4 位置误差曲线

在实验条件不变的情况下，进行了50次蒙特卡罗仿真测试，用姿态、速度和位置的均方根误差(Root Mean Square Error，RMSE)来衡量精度，用单位历元耗时衡量计算效率，并引入扩展卡尔曼滤波(Extended Kalman Filter, EKF)作为对比项，结果如表1所示。EKF算法由于对量测噪声建模不准确导致算法估计精度急剧下降，而方案1和方案2估计精度优势明显。方案1计算负担偏大，这是因为滑动窗中新息序列存储及求和运算占用了计算资源，方案2在噪声方差估计中只求解对角元素，通过可实现对独立变化的噪声进行跟踪调节，计算量相对减少。

表1 不同算法估计性能比较(RMSE)

为了进一步讨论算法性能，引入另一评价指标即新息加权指数

当值接χ2近于1，滤波对噪声估计准确，滤波趋向最优。χ2不仅能反应滤波对噪声的估计精度，还能体现对噪声跟踪能力的好坏。图5中分别设置方案1中的ρ值和方案2中的N值，发现ρ和N的取值与χ2参数值相关，不合适的取值会直接影响自适应滤波的跟踪性能，甚至引起滤波发散。

综上所述，时变噪声环境下的GNSS/SINS紧耦合导航系统中，本文讨论的优化算法能够保证滤波稳定性和精度，且更适合工程计算应用。

4 结论

本文讨论了一种基于逆Gamma分布的变分自适应滤波算法，该算法顾及量测噪声的时变性对独立变化的量测噪声进行跟踪调节，精化了系统随机模型，提高了算法的鲁棒性。数据测试表明该方法能有效实现噪声量测方差不准确或突变时的参数自适应估计，拥有较高的滤波精度，且计算负担小易于编程实现。将该算法用于含时变观测噪声的紧组合导航系统中，可为导航工程研究提供了一定的参考价值。