基于CFD浮空器阀门流量的研究

刘 特

(中国电子科技集团公司第三十八研究所 浮空平台部，合肥 230088)

0 引言

阀门是工业上广为应用的流体输送系统中的控制部件，具有截止、调节、导流、稳压、分流等作用。目前工程技术中用于阀门选型的参考资料主要是手册[1]和标准[2]。实际上，这些参考资料多是工程经验或者试验的总结[3]，且主要适用于液体管道或者气体管道[4]。虽然研究人员对阀门的流量、流阻特性和流动特性进行了大量的研究[5-17]，但阀门流量与阀门直径、阀门行程、流体压力差等参量之间依然缺少比较准确的定量关系。

高空浮空器阀门是浮空器内部压力控制和高度调节的重要部件，与其他阀门一样，一般采用工程估算的方法进行选择，缺少比较准确的设计原则和优化方法[18-19]。目前，进行高空浮空器阀门设计的主要理论依据是气体在压力差驱动下通过阀门将部分压力差转为气体动能，可用如下表达式进行估算：

式中：Q是质量流量；A是阀门口的面积和阀盖阀门围成面积中较小的面积；Δp是压力差；ρ是气体密度；C是流量系数，一般小于1。C的选取主要依靠工程经验或者实际测量，选取范围一般介于0.4～0.7之间，均值为0.55，取值范围相对均值的波动幅度约为27.27%，变化范围比较大。

为解决浮空器阀门设计时确定C过于依赖工程经验或者实际测量的问题，本文对浮空器的空气放气阀结构进行简化，突出其主要结构进行建模，利用计算流体力学(CFD)软件通过数值模拟方法得到气体流量与各参数之间的函数关系，在此基础上获得较为准确的阀门选型估算方法，并对阀门选型给出改进建议。

1 放气阀门参数化建模

图1(a)所示为浮空器空气放气阀门。根据该阀门的实际结构特点，在建模时对其结构进行简化处理，忽略放气阀的驱动机构和密封胶圈等细节部位。考虑到放气阀阀体为圆柱形，且阀门开启后气体流动主要在径向，沿圆周方向变化不大的特点，将放气阀门简化为绕中心轴线的平面二维几何模型，如图1(b)所示。简化后的模型几何参量主要有阀门半径R、阀门盖半径r和阀盖上升行程H(图1(b))。

(a)

2 计算方法及结果分析

2.1 计算方法

当阀盖行程距离为0时，浮空器空气放气阀门的气体流量为0；当无阀盖时，即阀盖行程为无穷大时，气体流量为最大；当阀盖行程为有限值时，气体流量介于0和最大值之间。在几何尺寸和压力差保持不变的情况下，阀门的气体流量随阀盖行程的增大呈单调递增关系，二者之间的函数关系可表示为

式中：H为阀门行程；Q0为阀门气体流量的最大值；τ为待定参数，具有长度量纲。

为方便采用最小二乘法求待定参数τ，引入空气流量的统计量参数Y

根据前述的阀门几何模型，利用CFD软件进行建模、网格划分和计算参数设置，图2所示为浮空器空气放气阀门几何模型网格划分图。根据图2对无阀盖、阀盖行程不同及半径和压力不同情况下浮空器放气阀门流量系数进行分析，即求解式(2)和(3)中的待定参数τ。

图2 浮空器空气放气阀门几何模型网格划分图

2.2 计算结果及分析

2.2.1 无阀盖

在阀门打开的时候，阀盖起阻碍气体流动的作用，可知，无阀盖情况下的气体流量为给定压力差下所分析阀门的最大流量。表1所示为阀门半径、压力差不同时，无阀盖阀门的气体流量及相应的C值。由表1可见，在无阀盖的情况下，阀门的C值介于0.5911～0.6076之间，且半径相同时压力差越大，C值越大。此外，表1中的C值略低于无粘性不可压缩二维自由射流的理论值(0.61[20])，这是因为实际气体不同于二维无粘性不可压的理想气体，存在粘性摩擦损耗和三维效应，流体能量有损耗。计算所得的流量系数略小于无粘性不可压流体的理论值，表明流量系数计算是合理的。根据表1，在工程估算中流量系数可以取0.6。

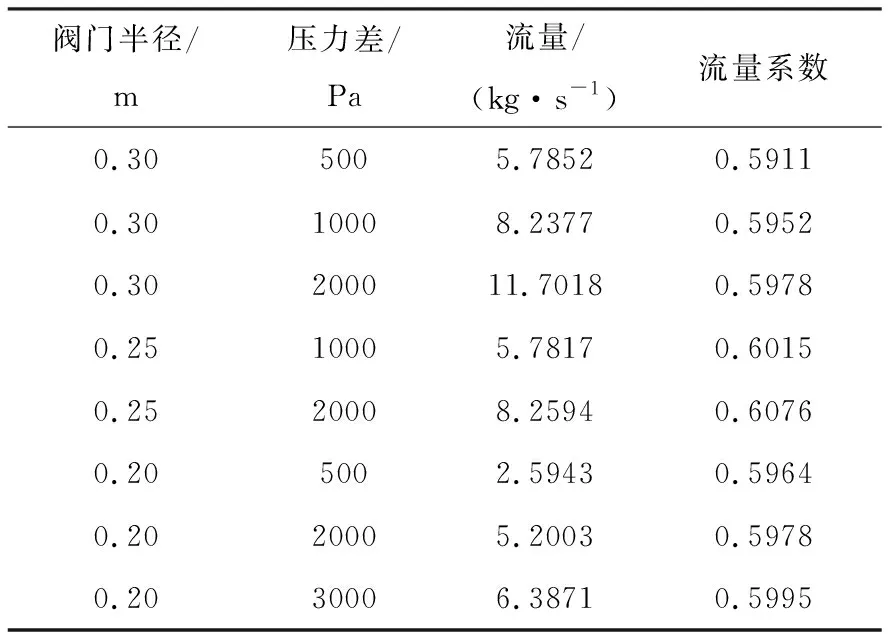
表1 阀门最大流量和流量系数

2.2.2 阀盖行程与阀门流量间的关系

在确定阀门的最大流量后，就可对阀门流量与阀盖行程间的关系进行分析。根据式(3)可知，空气流量的统计量参数与阀盖行程曲线的斜率为1/τ，为此，将模拟所得结果用统计量参数和阀门行程的关系图表示。

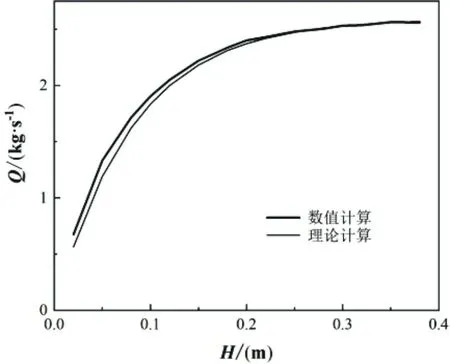
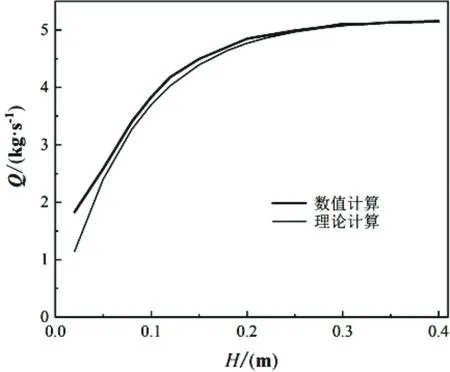
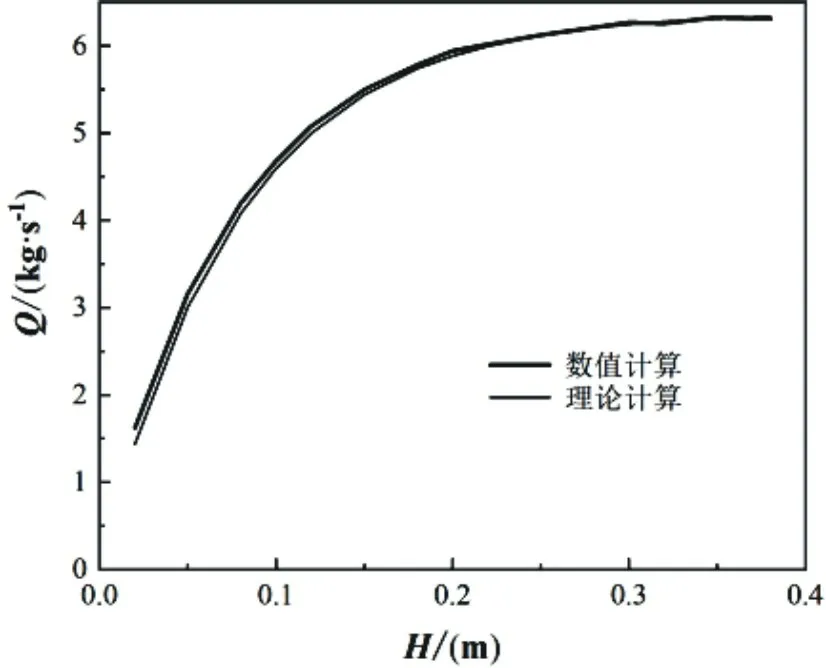
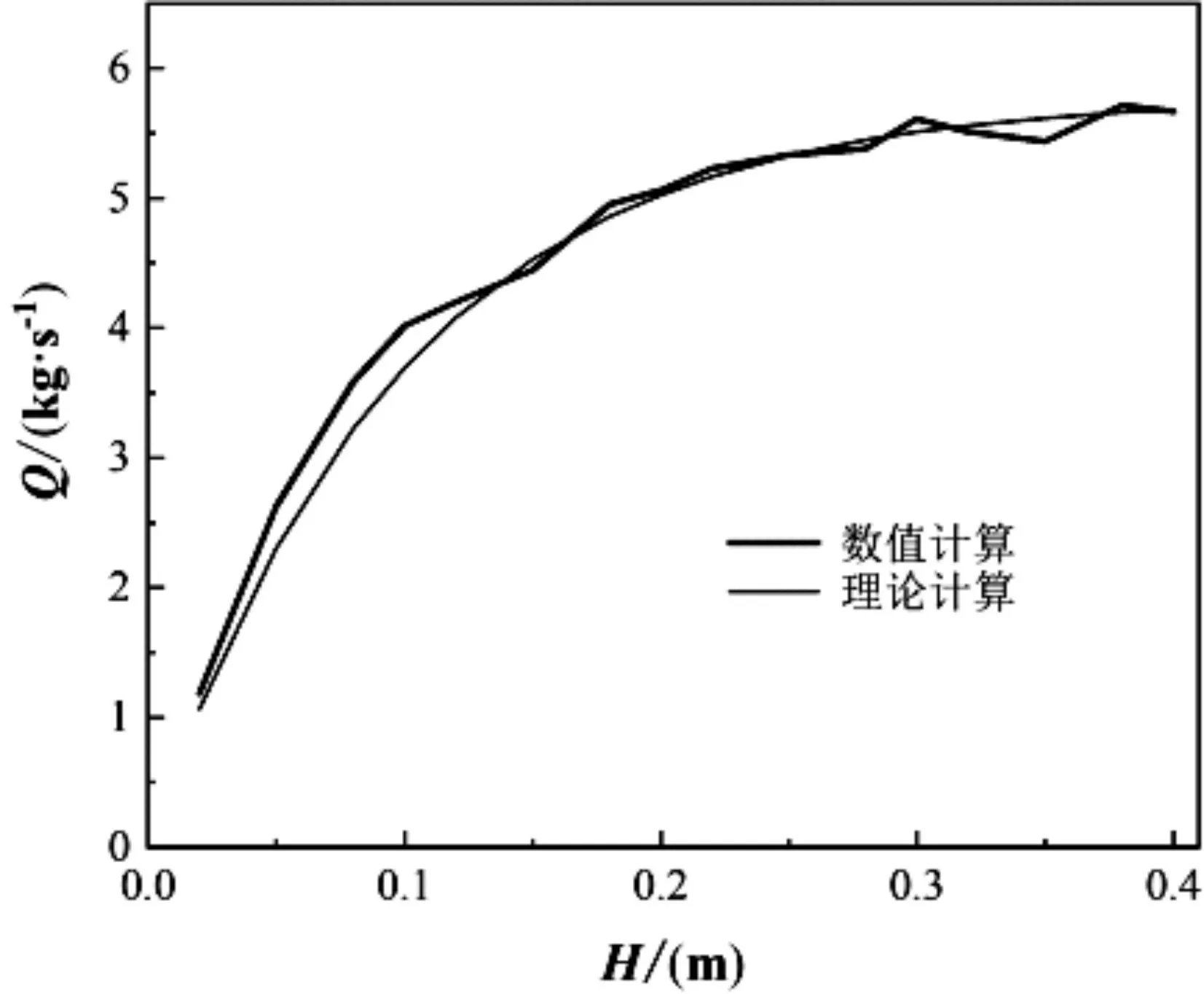
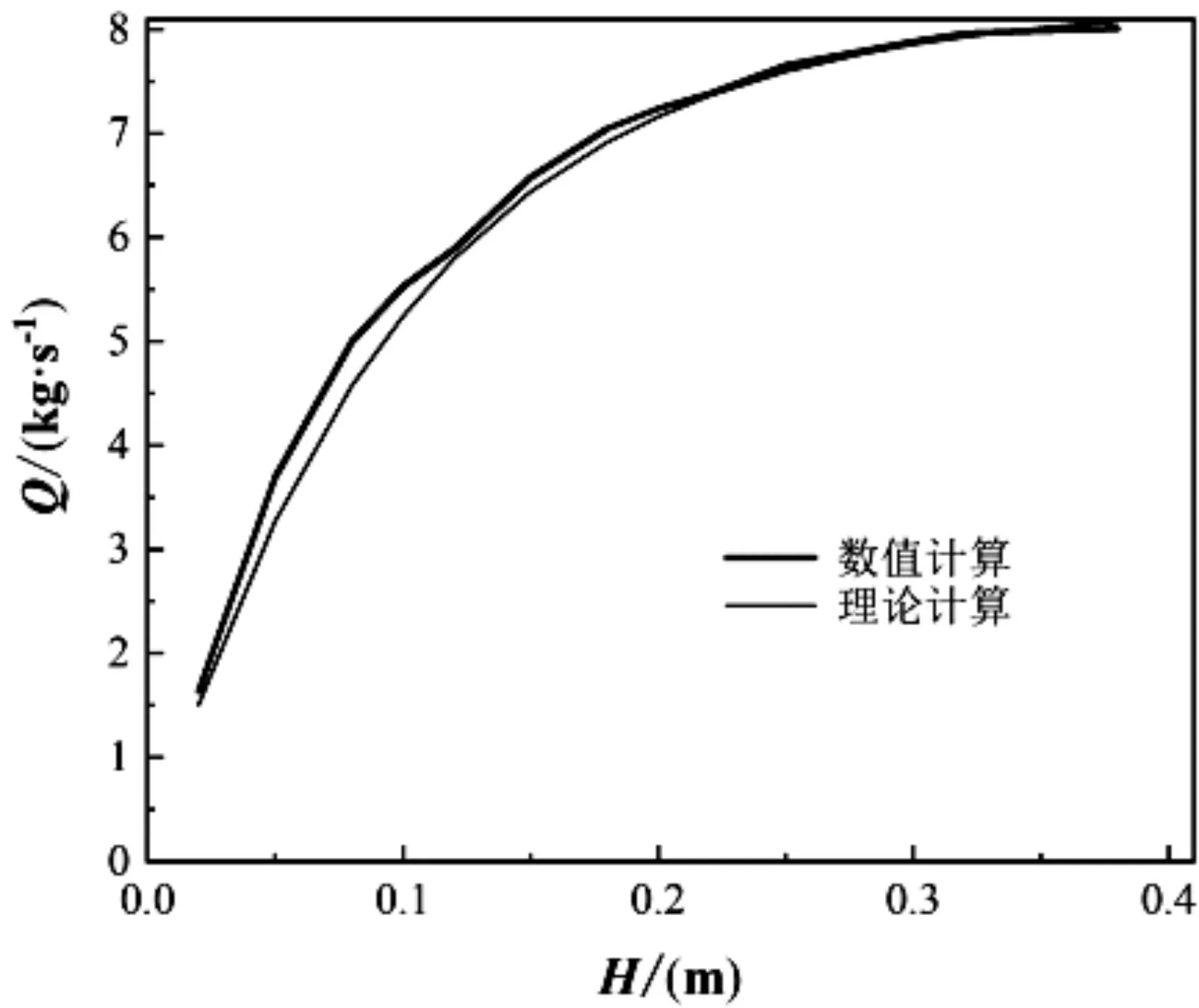
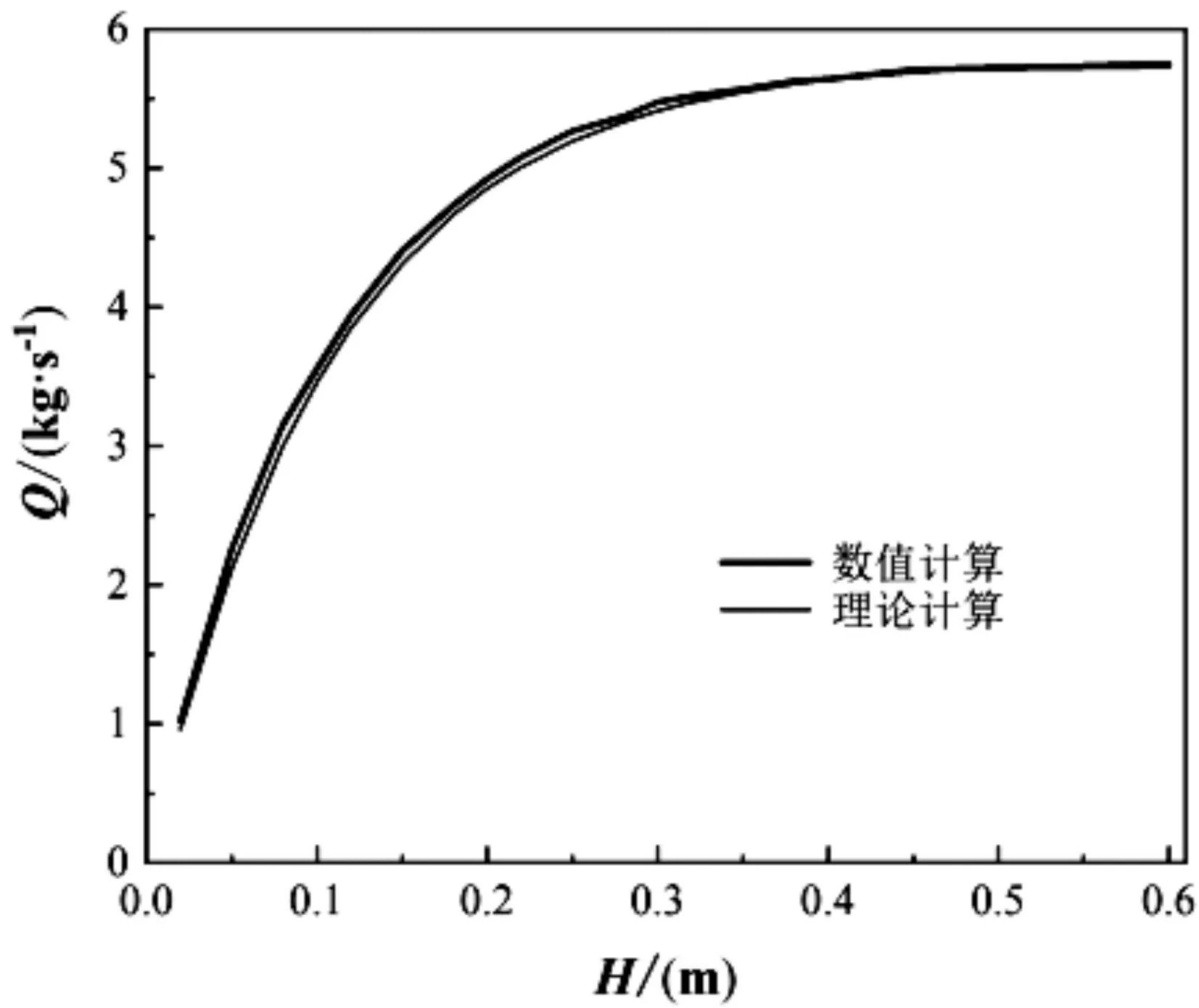
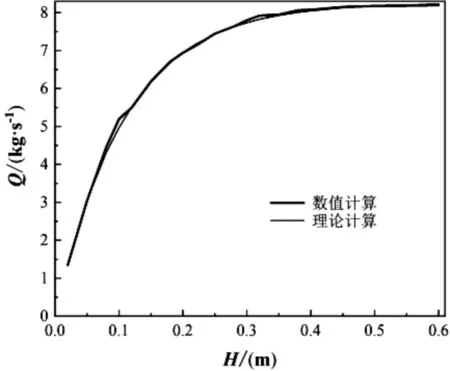
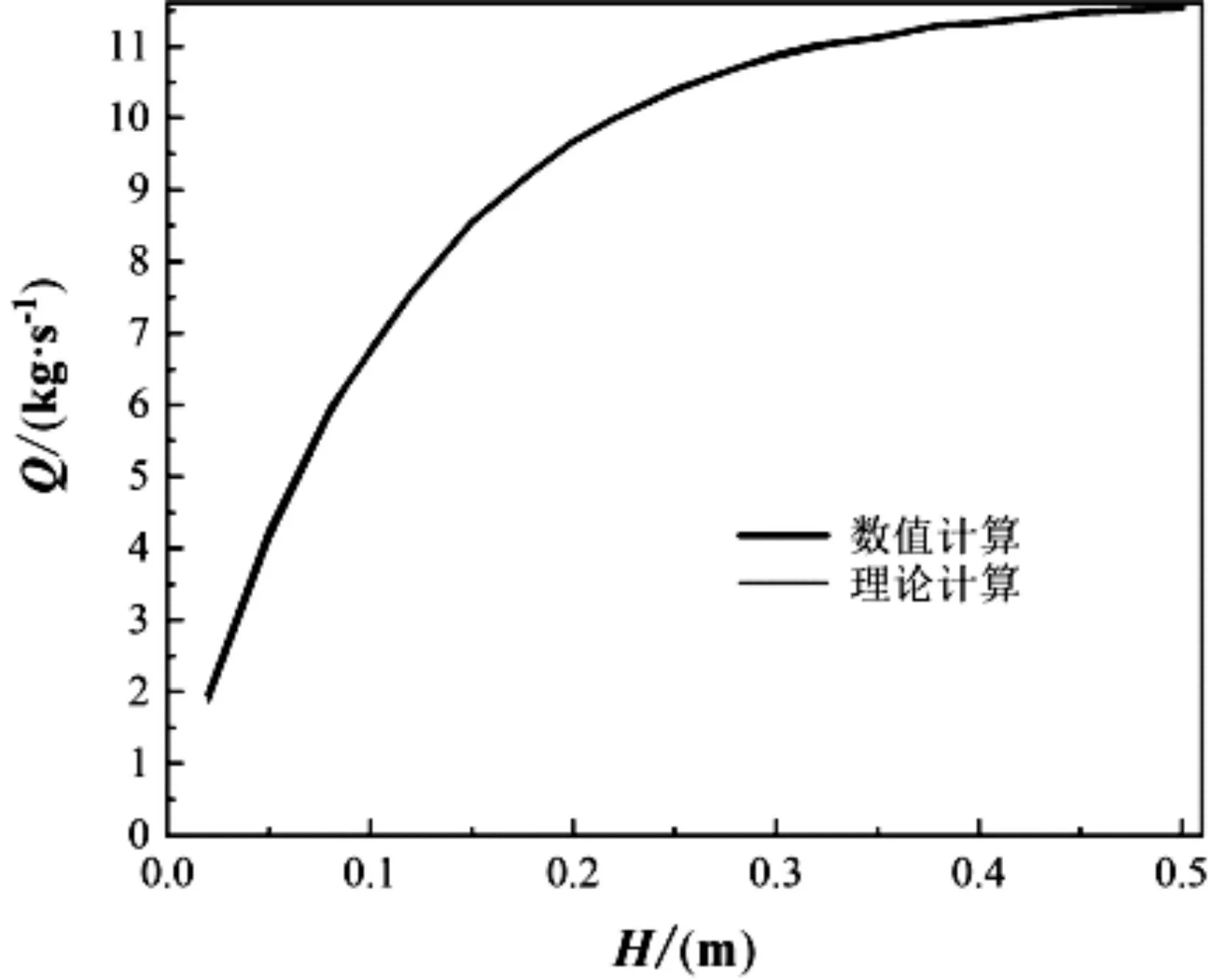
图3～图10所示为不同压差条件下阀门流量与阀盖行程之间关系的计算结果，其中，图3～图5、图6和图7、图8～图10所示分别为阀门半径为0.20 m、0.25 m、0.30 m的计算结果。图3～图10中(a)图的粗实线为CFD数值计算结果，细实线为理论计算结果，(b)图中的直线为根据统计量参数数值计算结果进行线性拟合所得。由图3～图10可见，当阀门半径为0.20 m和0.30 m时数值计算所得的阀门流量与理论计算所得结果吻合良好；当阀门半径为0.25 m时，数值计算所得的阀门流量波动较大，但数值计算结果与理论计算值吻合较好。

(a)

(a)

(a)

(a)

(a)

(a)

(a)

(a)

由图3～图10还可见，Y随H的变化与Q不同：当H为0 ～ 0.3 m时，Y和H之间的关系成近似线性关系；当H>0.3 m时，Y随H的增大波动幅度越来越大。表2所示为不同条件下Y和H之间的拟合方程表达式及其线性相关系数。由表2可知，不同条件下Y和H之间的线性相关系介于0.9400和0.9993之间，说明Y和H两者的线性相关性强。

2.3 计算结果讨论

由表2可见，在给定阀门半径条件下，当Δp变化较大时，τ(表2中线性拟合方程斜率的倒数)变化非常小。据此，可以引入修正流量参数Cr，其表达式如下

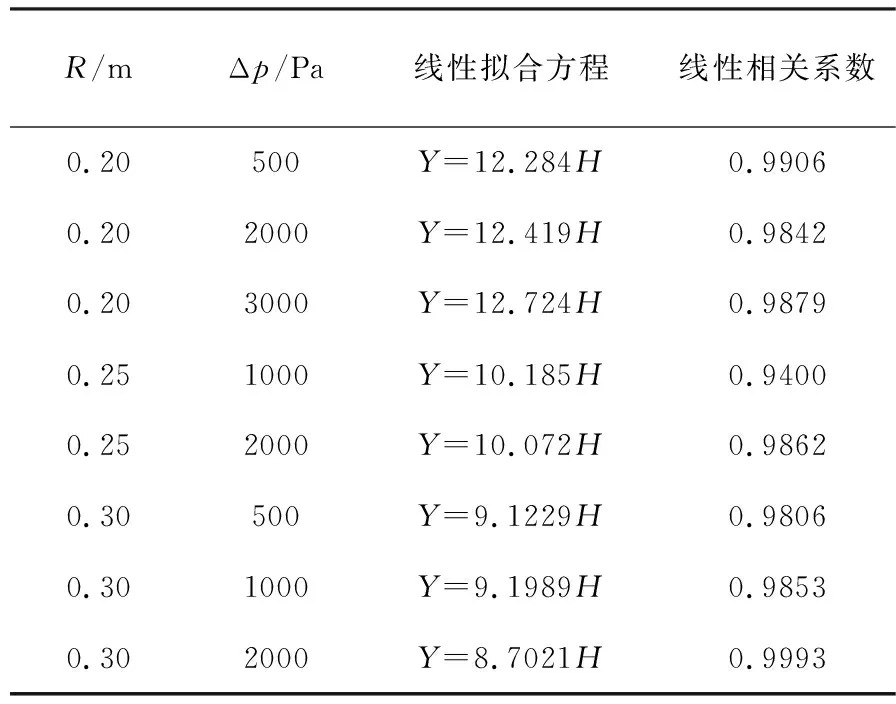
表2 不同条件下Y和H的线性拟合方程及线性相关系数

计算所得Cr列于表3。

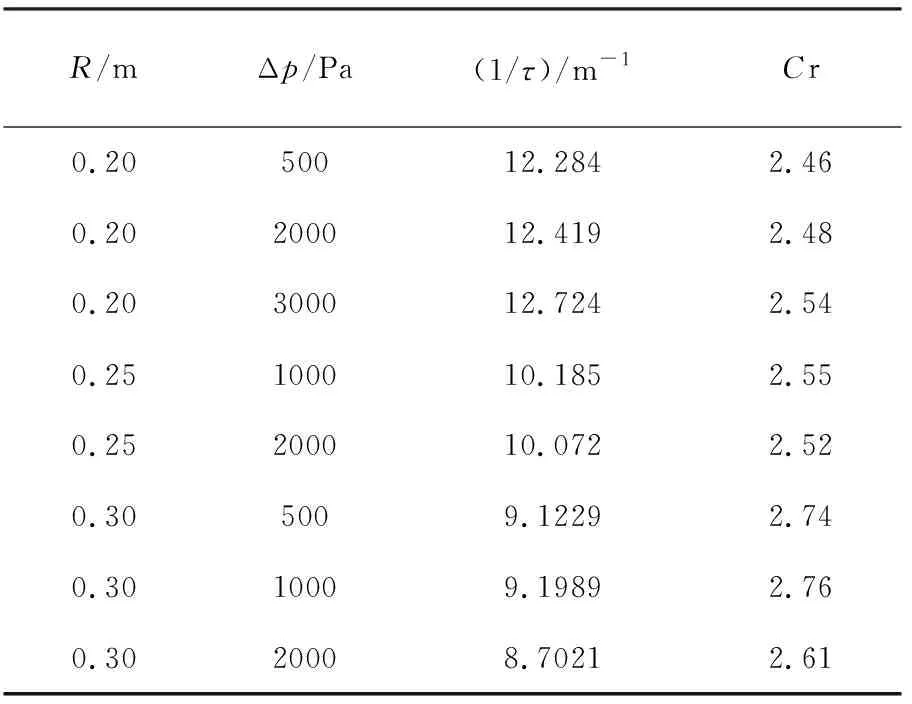
表3 不同条件下计算所得修正流量参数

从工程角度来看，可以近似认为在给定阀门半径条件下τ不随着Δp变化而发生改变。由表3可知，Cr的变化范围在2.46～2.76之间，均值为2.61，Cr相对于其均值的变化幅度约为5.75%，远小于C相对于其均值的波动幅度。因此，在工程估算中，和C一样，可将Cr视为常数，且用Cr来估算C可提高工程估算的准确度。

根据上述分析结果，在给定阀门半径条件下，可得阀门的最大流量为

当阀盖行程为H时，有

即

由式(6)可见，对于给定的阀门，当阀盖行程确定时，H/R为常数，C只与Cr有关，与Δp和R无关，这与阀门使用的工程经验相一致，说明这样的估算是合理的。

3 结论

根据实际使用条件，采用CFD数值模拟方法对浮空器空气排气阀门的气体流量和阀门半径、压力差、阀盖行程之间的关系进行了计算。通过引入统计量参数对计算结果进行分析，得出如下结论：

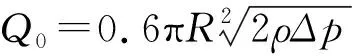
(3)从工程应用角度来看，阀门半径R与τ之间的比值(修正流量参数Cr)近似为常数，且可用Cr的值来估算流量参数C；

(4)对于给定的阀门，当阀盖行程确定时，流量参数只和Cr有关，与Δp和R无关。