基于数学模型的发动机舱盖锁舌曲面优化
陈瑜 周星栋


摘要: 针对发动机罩非正常下落导致无法锁止的问题,推导非线性微分方程并采用泛函求解,将工程问题转化为力学数学模型。根据数学模型优化发动机舱盖锁舌曲面,采用有限元法搭建仿真模型。分析结果表明,基于数学模型的有限元法可以高效准确地模拟发动机舱盖关闭过程中锁的实际运动过程,优化结果可为发动机罩锁舌优化提供思路。
关键词: 锁舌;数学模型;优化;有限元;Abaqus
Abstract: As to the lock failure of the engine hood under unexpected falling, the nonlinear differential equations are deduced and then solved by generalized functions, and then the engineering problem is transformed into mathematic models of mechanics. The locking tab shape of engine hood is optimized by the mathematic model, and the finite element method is used to build the simulation model. The analysis results show that the actual movement process of the lock during the engine hood closing is efficiently and accurately simulated by the finite element method based on the mathematic model, and the optimization results can provide ideas for the optimization of the engine hood locking tab.
Key words: locking tab;mathematic model;optimization;finite element;Abaqus
0 引 言
随着工业制造的不断创新和计算机仿真的持续发展,有限元仿真成为汽车、航空航天等行业技术开发流程中的重要组成部分。利用有限元法可精准再现物理载荷工况中的问题,通过应力应变分析可探索解决问题的关键,因此基于有限元的优化設计方法得到广泛应用。[12]如何提高仿真优化方案的精确度是工程开发过程中需要重点考虑的问题之一。
本文以实际产品为例,采用有限元法模拟工程问题,通过应力应变分析确定产品结构的优化方向,结合相应的数学模型提出优化方案并进行验证。优化后物理样件的二次试验验证该方法可以提升车辆零部件结构优化的效率和精准性[34]。
1 物理载荷工况
某车型发动机舱盖处于最高位置下落时,由于关闭速度过大,发动机舱盖锁罩壳被砸坏或锁钩无法正常拨动锁舌,使得发动机舱盖无法正常关闭。按照设计原理,当发动机舱盖打开至正常高度关闭时,锁钩的运动轨迹为图1(a)中1号轨迹。在实际使用中,用户误操作使得发动机舱盖在最高位置下落,关闭过程中锁钩运动速度过快,导致整个锁舌断裂或锁钩运动轨迹偏移,见图1(a)中2号轨迹。锁钩直接撞击锁罩壳会导致整个锁结构损坏。
在新车开发过程中,通常是同平台的多款车型共用一个发动机舱盖锁模块,其结构更改对诸多车型的开发都将产生很大影响。因此,提出一种切实可行、适用同平台车型的解决方案,是发动机舱盖锁模块优化的重点。
2 有限元模型
有限元分析利用数学近似的方法对真实物理载荷工况进行模拟,即利用有限数量的单元搭建相应的模型,重现真实或试验的物理工况。[56]
2.1 有限元模型建立
利用前处理软件ANSA将发动机舱盖的相关零件离散成5 mm的壳单元,发动机舱盖有限元模型见图2。采用六面体单元模拟发动机舱盖内外板之间的胶水,通过柔性连接的方式模拟焊点连接2个钣金结构,采用释放轴向自由度的铰链单元模拟铰链处的螺栓。在发动机舱盖关闭过程中,锁钩直接与锁舌发生接触,为定义两者的直接接触关系,将锁钩定义为表面包裹一层壳单元的体单元。
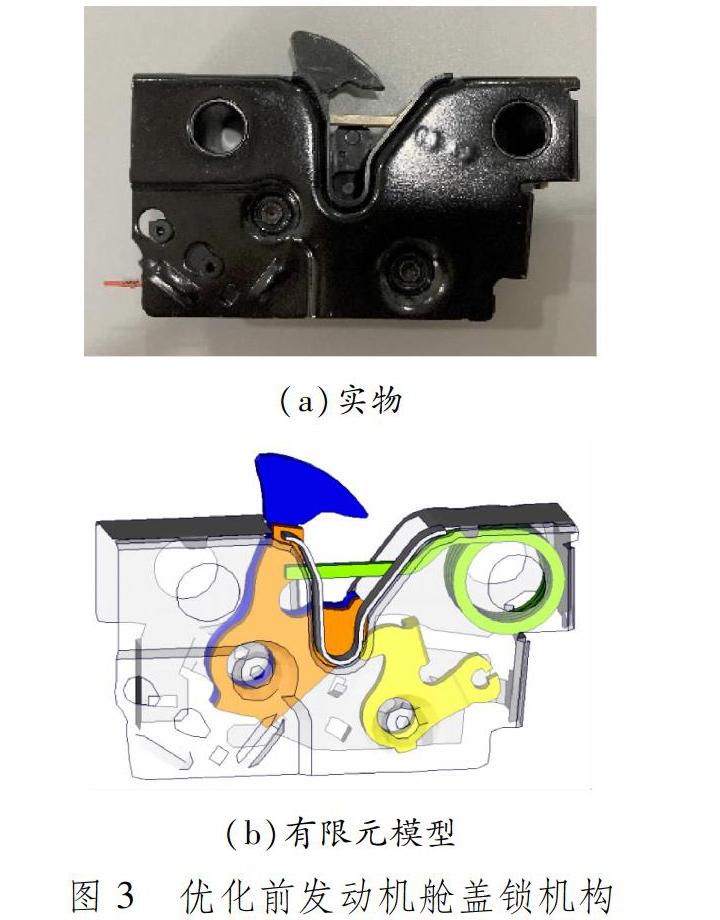
在整个物理载荷工况中,发动机舱盖锁模型的搭建至关重要。舱盖锁内部机构之间采用铰链单元JOINT和弹簧单元SPRING相结合的方式连接,从而模拟整个锁结构。[79]优化前发动机舱盖锁实物和有限元模型见图3。
2.2 试验关闭工况模型
基于发动机舱盖和锁的有限元组装模型,根据物理载荷工况,定义与试验相匹配的仿真边界条件、初始条件和加载条件。将发动机舱盖的初始位置定义为锁钩和锁舌接触零时刻的位置,并向整个发动机舱盖施加初始速度V0,定义发动机舱盖旋转铰链轴心到锁钩处的半径为R,则发动机舱盖铰链轴的旋转角速度为ω=V0/R。
根据实际汽车发动机舱盖运动限界定义相应的边界条件,见图4。发动机舱盖铰链处约束除y向转动以外的其他5个自由度,同时增加落水槽密封条处的y向约束以及缓冲块对应的车身匹配面和锁的6个自由度约束。
采用有限元仿真软件Abaqus模拟发动机舱盖不同速度下的关闭过程。正常速度(V0=1.6 m/s)关闭工况和高速(V0=4.6 m/s)关闭工况时发动机舱盖锁钩运动过程分别见图5和6,2种工况下锁钩的运动方式明显不一样。
在高速关闭过程中,锁钩滑过锁舌后直接滑向锁罩壳,导致锁钩和锁罩壳破碎失效。对比物理试验的失效情况,两者吻合很好,因此基于该物理工况的有限元模型能精确反映实际问题,可为后续的优化提供基础模型。
3 优化方案
因为模块件的改动涉及到整个结构和周边匹配结构的重新开模,影响很大,所以尽可能通过局部改动满足需求。通过应力应变有限元分析,最终将优化方案确定为锁舌型面的优化。传统的型面优化方法主要依靠工程师的经验或利用优化软件不断尝试,不仅浪费人力和计算资源,而且优化结果也可能存在工艺和制造方面的问题。为更加高效地得到满足要求的优化曲面,避免重复计算多个锁舌曲面的性能,将物理工况转化为数学模型,通过相应曲面函数的优化,提高求解效率和精确度。[1011]
3.1 数学模型建立
针对发动机舱盖关闭的运动过程,可以从物理意义上将发动机舱盖简化为1个质量球,令其在高度H的位置以自由落体的方式落下,锁舌曲面定义为小球的滚动曲面。发动机舱盖关闭工况简化模型示意见图7,其中:m为小球的质量;F为离心力;G为重力;r为小球运动轨迹的曲率半径;C1和C2为锁舌尖端尺寸参数;θ为小球运动方向与水平方向的夹角。根据发动机舱盖的关闭工况,需要保证小球沿曲面切向运动且不能脱离曲面,即两者之间的接触力应大于或等于0。
3.2 锁钩曲面微分方程
基于简化的数学模型,假设锁钩曲面光滑无摩擦,忽略小球滚动引起的自转。这2个假设使得小球运动速度更快、离心力更大、更容易脱离曲面,因此相关设计偏保守。
4 优化方案的试验校核
根据有限元法的优化结果重新开模并制作新锁舌,优化后的发动机舱盖锁实物见图10。
根据实际工况,对发动机舱盖高速关闭进行物理试验。通过高速摄像机拍摄的影像可知,即使在发动机舱盖高速关闭工况下,优化后新发动机舱盖锁也能很好地达到锁止状态。在发动机舱盖高速关闭过程中,锁机构在不同时刻试验与仿真的位置对比见图11。由此可知,基于数学模型的有限元法能高效精准地反应物理载荷的实际情况。
5 结束语
本文以数学模型结合有限元仿真,避免传统虚拟分析的烦琐流程,高效精准地解决发动机舱盖锁关闭损伤的实际问题。该方法突破传统的有限元优化流程,引入基于物理载荷工况的简化数学模型。首先,通过力学方程推导得到曲面微分方程的最优解;然后,利用有限元法验证优化方案的可行性;最后,通过样件试验验证优化方案的准确性。
学模型的有限元法可以避免烦琐的方案推演,提高有限元优化的效率和精准度,节省样件模具制造费用和试验费用。研究结果表明,该方法可以用于汽车和其他制造业的开发设计,是一种高效精准的优化设计方法。
参考文献:
[1] 王若平, 羊杰, 丁华, 等. 汽车轻量化与有限元分析[J]. 山东工业技术, 2016(10): 226227. DOI: 10.16640/j.cnki.371222/t.2016.10.198.
[2] TANG Y M, HONG W P, SONG M Y. Topology optimization and lightweight design of engine hood material for SUV[J]. Functional Materials, 2016, 23(4): 630635. DOI: 10.15407/fm23.04.630.
[3] 陈鸿宇. 汽车发动机盖锁安装点结构优化设计[J]. 内江科技, 2019, 40(4): 47.
[4] 张鸿荣, 雷金凡. 轿车车身发动机盖变形分析及焊点优化[J]. 电焊机, 2017, 47(9): 8589. DOI: 10.7512/j.issn.10012303.2017.09.18.
[5] QIU H Y, HUANG Y J, LIU Q. Study of engine hood panel forming based on numerical simulation technology[J]. Journal of Materials Processing Technology, 2007, 187/188: 140144. DOI: 10.1016/j.jmatprotec.2006.11.173.
[6] 龚益玲, 郑宁昆. 拓扑优化在铝合金发动机舱盖刚度计算中的应用[J]. 计算机辅助工程, 2020, 29(2): 7073. DOI: 10.13340/j.cae.2020.02.013.
[7] 聂根辉, 欧阳春平, 库才旗. 发动机罩锁扣磨损分析与工艺改进研究[J]. 汽车工艺与材料, 2017(4): 3942. DOI: 10.3969/j.issn.10038817.2017.04.010.
[8] 孫啸天. 汽车罩盖锁布置方法及结构发展[J]. 汽车工程师, 2017(7): 1617. DOI: 10.3969/j.issn.16746546.2017.07.005.
[9] 陈坚. 发动机盖锁弹簧的设计开发[J]. 汽车实用技术, 2017(16): 2527. DOI: 10.16638/j.cnki.16717988.2017.16.010.
[10] 程发超, 牛丽红, 苏秉华, 等. 基于微分方程数值解的自由曲面透镜的设计[J]. 光学技术, 2013, 39(3): 267271. DOI: 10.13741/j.cnki.111879/o4.2013.03.014.
[11] 蔡姗姗. 微分方程在曲线与曲面论中的运用研究[J]. 河池学院学报, 2019, 39(2): 4953. DOI: 10.3969/j.issn.16729021.2019.02.009.
(编辑 章梦)

