冲击载荷作用下单层球面网壳结构的破坏和温度效应

庞凯 胡亚超 席丰 谭英华

摘要： 基于材料的损伤和失效准则，考虑重物冲击和受火温度对钢材性能的影响，运用有限元软件Abaqus分析K8型单层球面网壳在不同温度范围受到冲击载荷时的失效模式。对693个网壳算例进行分析，根据网壳的竖向变形和塑性发展情况，总结K8型单层球面网壳在冲击载荷作用下的6种破坏类型和失效模式分布。研究结果表明：温度对网壳结构在冲击作用下的稳定性有较大影响;在冲击物质量和速度一定的前提下，当火灾温度达到某个限值时，网壳出现整体倒塌破坏;当火灾温度达到400 ℃时，结构的抗冲击能力明显降低;随着冲击物质量和速度的增加，网壳变形模式不再随着温度的升高发生明显变化，此时网壳失效类型以剪切破坏为主。

关键词： 网壳;火灾;失效模式;动力响应;金属损伤;失效准则;有限元

Abstract： Based on the damage and failure criteria of the material， the failure modes of K8 singlelayer reticulated dome subjected to impact load at different temperature are analyzed by finite element software Abaqus， in which the influence of heavy impact and fire temperature on steel properties is considered. The 693 cases are analyzed， and the vertical deformation and plastic development of the reticulated dome are analyzed， and then the 6 failure types and the failure mode distributions of the K8 singlelayer reticulated dome under impact loadings are summarized. The results show that： the temperature has a great influence on the stability of reticulated dome under impact;under the premise of a certain impact mass and velocity of the impact object， the reticulated dome collapses while the fire temperature reaches a certain limit;the impact resistance of the structure decreases obviously while the fire temperature reaches 400 ℃;with the increase of the impact mass and velocity， the deformation mode of reticulated dome no longer evidently changes with the increase of temperature， and the failure type of the reticulated dome is mainly shear failure.

Key words： reticulated dome;fire;failure mode;dynamic response;metal damage;failure criterion;finite element

0 引 言

网壳结构具有刚度大、自重轻、整体性能好等特点，被广泛应用于大空间建筑，如体育馆、展览馆等。近些年，针对高大空间建筑结构的袭击事件时有发生，此类建筑一旦遭遇恐怖袭击，将引发严重后果。

国内外许多学者已对高大空间建筑结构进行研究。刘晓等[1]对杭州国际会议中心裙房钢结构桁架体系曲面屋盖进行数值模拟，分析完善结构和带缺陷结构的大位移弹性整体稳定性和弹塑性稳定性，研究结果表明结构的整体稳定因数随载荷步增加而增大，结构的极限承载力可以通过切線刚度的奇异点确定，结构的整体稳定性因数较同种载荷工况下几何非线性整体稳定性因数显著减小。赵宪忠等[2]和ZHAO等[3]开展单层球面网壳结构整体模型的连续性倒塌试验研究，发现单根杆件破坏后局部内力重新分布使杆端节点出现失稳，引发周围节点依次向下运动，导致整体结构连续性倒塌，这是单层球面网壳结构遭遇局部初始破坏后倒塌的主要模式。丁阳等[4]根据单层网壳结构杆件的受力特点，提出单层网壳结构杆件的2种失稳类型，建立网壳结构杆件计算模型，并且模拟杆件在动力载荷作用下经历失稳、拉直和塑性铰形成至消失的过程。史建勇等[5]基于多学科的研究成果，建立空间整体结构的火灾结构耦合分析模型，采用系统集成方法提出复杂空间结构整体性防火分析模型并进行实例验证，结果认为耐火测试通用要求（ISO 834）中的标准升温曲线和空间均匀升温假定不适用于大空间结构，需要进行火灾结构耦合分析。薛素铎等[6]研究空间结构抗火性能，同样认为传统火灾升温曲线不适用于大空间建筑。杜咏等[7]通过数值试验的回归分析总结归纳适用于大空间结构的火灾升温经验公式。贺拥军等[8]发现火灾对网壳结构在爆炸作用下的动力稳定性有较大影响。FRIEDMAN[9]通过实验研究得到火灾热释放速率计算的经验公式。NELSON[10]研究发现火灾初期的增长可分为慢速、中速、快速和超快速4种类型。王多智等[11]和FAN等[12]研究网壳在冲击载荷作用下的失效模式，认为网壳竖向变形主要与杆件受力和冲击物的质量与速度有关。

上述研究均单独讨论网壳结构在火灾或冲击作用下的性能，而实际上火灾往往与重物冲击事故相伴发生。因此，研究单层球面网壳结构在火灾与重物冲击耦合作用下的动力响应十分必要。

本文利用非线性有限元软件Abaqus分析先受火侵袭后受重物冲击作用的单层球面网壳的动力响应，讨论单层球面网壳的破坏类型，并总结网壳的失效模式。

1 有限元模型

以K8型单层球面网壳为研究对象，其俯视图和正视图见图1。球面网壳跨度为40 m，矢跨比为1/5，网壳杆件选用无缝钢管，杆件截面的外径为102.0 mm，壁厚為3.5 mm，材料选用Q235钢。假定屋面载荷为1 kN/m2，将其等效为节点集中载荷施加在网壳节点上。

网壳周边采用固定铰支座约束，杆件单元和节点编号见图2，其中①～⑥为杆件编号，N表示节点。

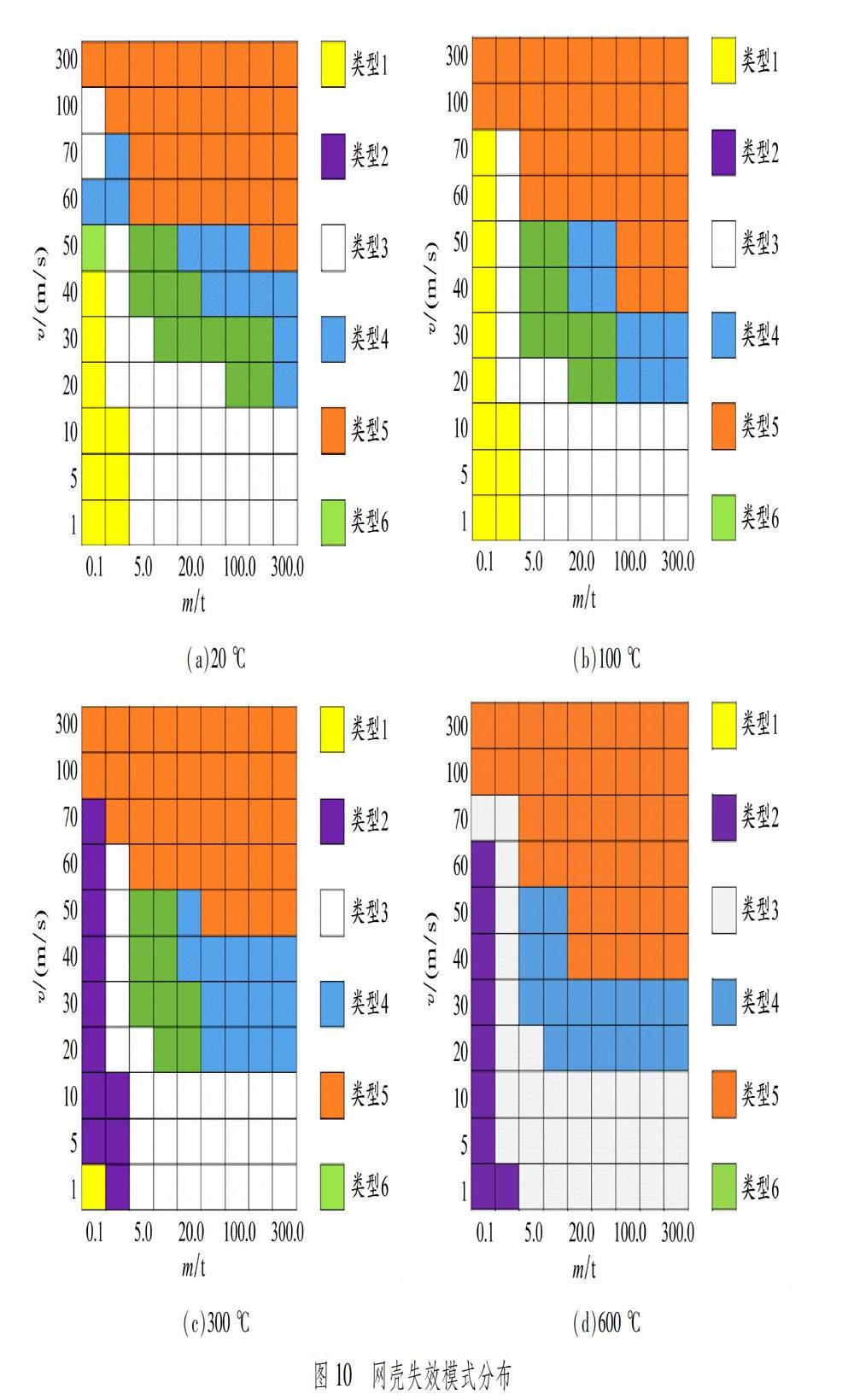
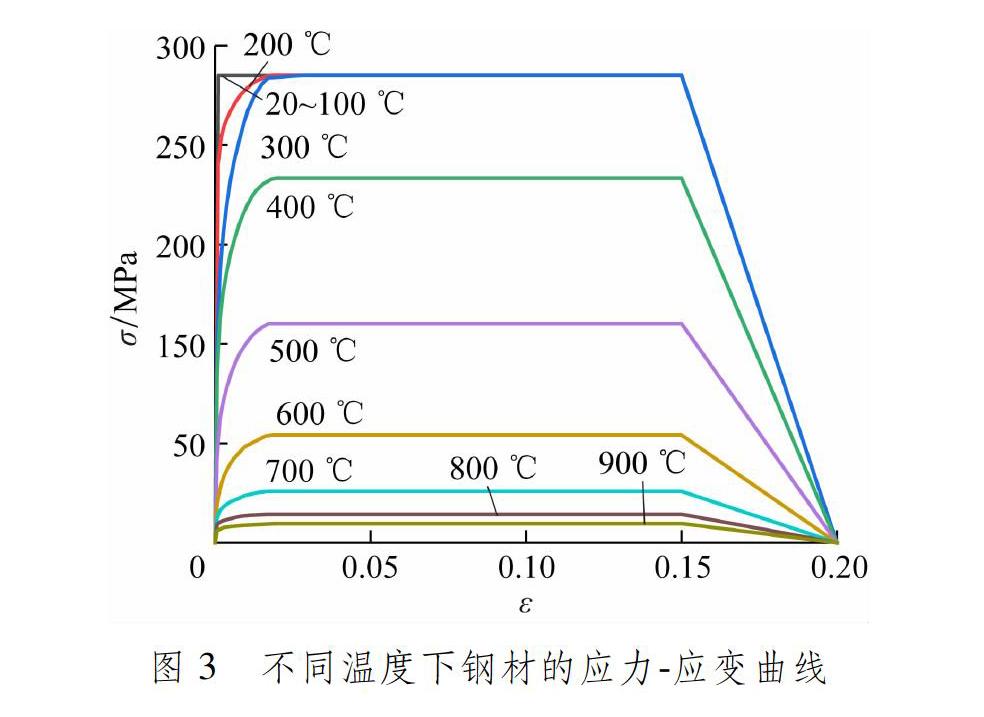
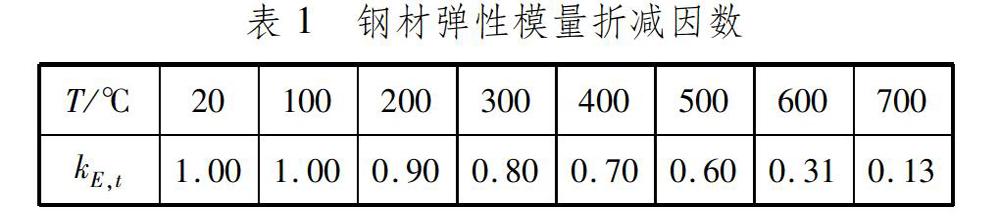
式中：Tx，z，t为t时刻距火源中心水平距离为x、垂直距离为z处的空气温度，℃;Tg（0）为火灾发生前大空间建筑室内的初始温度，常温取20 ℃;b为火源中心至火源最外侧边缘的距离;Tz为火源中心距离地面垂直距离为z处的最高温度，根据文献[13]附录D取值;β为升温曲线形状因数，按文献[10]附录D根据火源功率类型和火灾增长类型取值;η为距火源中心水平距离为x处的温度衰减因数，按文献[10]附录D取值，当x

本文采用传统升温曲线（ISO 834），通过式（1）换算得到空气升温曲线，然后采用增量法得到网壳杆件的温度曲线。

火源功率设计值按大功率火灾取25 MW，此时可将火源模型简化为底部直径7.98 m、高5.36 m的圆锥体，无保护层网壳结构的初始温度为20 ℃。

1.2 高温下钢材的物理性能

1.3 高温下Q235钢的力学性能

高温下Q235钢的弹性模量和应力应变关系均与常温下有不同程度的变化。常温下Q235钢的弹性模量取E=206 GPa，高温下Q235钢的弹性模量参照BS EN 199312： 2005标准规定进行折减。钢材弹性模量折减因数kE，t=ET/E， ET为高温下钢材的弹性模量，kE，t取值见表1。

1.4 温度与应变率共同作用下Q235钢的本构模型

冲击问题属于强非线性瞬态动力学范畴。钢材的屈服应力会因应变率敏感性而提高，因此应变率对结构的抗冲击能力有重要影响，应变率效应不可忽略。采用依据应变率效应的CowperSymonds本构模型，钢材的动态屈服强度σd可表示为

为钢材的等效塑性应变;Q为钢材的黏滞参数;q为钢材的应变率硬化参数。在常温下，Q和q可以分别取40 s-1和50;当温度达到1 000 ℃时，据文献[15]，Q和q分别取400 s-1和1。将常温和1 000 ℃时的应变率参数进行插值，可以得到与温度相关的2个应变率参数Q（T）和q（T）。[15]

1.5 材料失效准则

在等向强化弹塑性材料中，损伤表现为应力软化和刚度退化2种形式。考虑损伤时钢材的应力应变曲线见图4。

σy0和0分别为损伤开始时的应力和等效塑性应变，f为钢材失效时的等效塑性应变。D为控制刚度退化程度的损伤变量，D=0以后的实线表示损伤后的应力应变关系，虚线表示不考虑损伤时的应力应变关系。材料损伤前D=0，材料完全失效时D=1，因此可将D=1作为删除单元的失效准则。

在具体的有限元模拟中，若要考虑材料的损伤和失效，则应力应变关系不能准确反映材料的真实行为。从初始损伤到最终失效，等效塑性应变0的发展与单元特征长度有关，即图4中的下降段具有较强的网格依赖性。因此，对于应力应变曲线的应变软化部分，需要采用不同的方法处理。断裂能方法可以在损伤开始后通过创建应力位移关系减少网格依赖性。利用脆性断裂概念，定义开始出现单位面积裂缝所需的能量Gf为材料参数，因此损伤开始后的软化响应可以表示为应力位移关系，而不以应力应变关系为特征。

在Abaqus中，定义与积分点相关的特征长度为L，则由断裂能得到的应力位移关系为。特征长度L取决于单元的几何形状，对于梁和桁架，L是指沿单元轴的特征长度。

在定义等效塑性位移后，可以进一步定义材料的损伤累积和失效过程，韧性金属的每一种损伤起始准则都有相应的演化规律。损伤演化规律既可以用等效塑性位移表示，也可以用断裂能耗散Gf表示，两者都考虑单元的特征长度从而减轻网格依赖性。

本文采用基于有效塑性位移的损伤演化规律，一旦到达损伤起始点，有效塑性位移就满足损伤变量随相对塑性位移的变化曲线，即材料失效准则见图5。

2 计算结果分析

2.1 火灾下网壳结构的力学性能

依据上述火源模型，火灾发生后6 000 s内各节点处的温度曲线见图6。

假定火灾下网壳杆件内温度均匀分布，根据文献[13]中无保护层钢构件升温计算公式可得到火灾下网壳杆件的温度曲线，见图7。

在火灾发生初期，杆件温度增长较慢，随后温度迅速增长;当火灾持续至3 000 s时，温度增长速度减缓。杆件温度最高可达600 ℃，网壳顶点附近温度较高，且节点离火源水平位置越近，其温度增长速度越快。俯视图中的网壳中心区域温度明显高于外层，最外层4个环的杆件最高温度为300～400 ℃。

将所有网壳杆件置于上述温度曲线所表征的火灾环境中，计算得到火灾下网壳各节点的位移曲线，见图8。高温下网壳结构主要表现为因杆件热膨胀而产生的向上位移，且随着温度升高，位移不断增大，网壳顶点处位移最大，火灾持续至6 000 s时，顶点位移约为0.26 m。

2.2 温度和撞击载荷共同作用下网壳的动力响应

虽然冲击载荷是偶然载荷，但在现实中，冲击物的质量和速度取值范围很广，质量可能是几吨到几十吨、速度可能超过100 m/s，也有因施工操作失误产生的速度相对较小、质量只有几百克的冲击物。本文模拟冲击物质量分别为0.1、1.0、5.0、10.0、20.0、50.0、100.0、200.0和300.0 t，速度分别取1、5、10、20、30、40、50、60、70、100和300 m/s。

计算假定：（1）只考虑动能和内能的变化，不考虑热能的损失;（2）冲击物竖向冲击网壳顶点，应力波瞬间传播到网壳结构的各个部分;（3）忽略冲击物与被冲击物间的摩擦作用;（4）忽略冲击物与被冲击物间的阻尼;（5）冲击物为刚体。

参照文献[8]将网壳结构最内圈杆件温度定义为网壳结构所处的火灾温度，分析不同温度阶段受撞击网壳的动力响应。

通过693个K8型单层球面网壳结构算例的动力响应分析，将高温和冲击载荷共同作用下K8型单层球面网壳的破坏类型分为6类，见表3。

类型1为网壳未破坏，杆件轻度损伤，无杆件进入塑性变形且竖向变形较小，网壳整体变形不大。

类型2为网壳未破坏，杆件轻度损伤，内环杆件进入塑性变形，竖向变形较大。

类型3为结构持续性碰撞倒塌，冲击物与网壳经历1次或由于冲击物被弹起而产生的多次较短时间的碰撞，冲击物与网壳经历较长时间的持续接触，并且在网壳变形较大时持续冲击网壳，导致网壳凹陷范围逐渐扩大至整个结构，最后结构整体翻转，冲击物将网壳穿透，进而造成网壳破坏。

类型4为结构瞬间碰撞倒塌，冲击物和网壳经历1次或由于冲击物被弹起而产生的多次较短时间的剧烈碰撞后将网壳穿透，网壳继续变形，凹陷范围扩大至整个结构，进而引起网壳整体下翻破坏。

类型5为网壳结构局部凹陷失效，冲击物与网壳碰撞接触后，冲击作用致使网壳产生凹陷，随后网壳被冲击物穿透，网壳结构凹陷范围由冲击区域向外扩展，但未扩展至网壳整体。

类型6为杆件剪切失效，冲击物速度较快，受冲击杆件瞬间破坏，冲击作用破坏区域仅限于网壳与冲击物接触的区域，且破坏时冲击物与网壳尚未分离，网壳破坏区域对其周围区域的影响不大，只有杆件发生破坏，网壳没有产生明显凹陷。

温度为20、100、300和600 ℃时网壳的失效模式分布见图10。

对比不同温度下网壳的失效模式和竖向变形可以发现，在所有温度下，低速大质量的冲击比高速小质量的冲击对网壳结构破坏作用大。在低速大质量的撞击作用下，网壳容易发生整体的倒塌破坏;在高速小质量撞击作用下，网壳结构一般以局部剪切破坏为主，不会发生倒塌破坏。

由图10（a）～（c）可知：当冲击速度和质量较小时，随着温度的升高，网壳的破壞类型由类型1向类型2过渡;当火灾温度超过300 ℃时，类型1的破坏已不存在。由于温度对应变率效应的影响，使得高应变率下钢材的强化能力降低，温度为200～300 ℃时钢材弹性模量减小，导致网壳竖向位移增大。

由图10（c）和（d）可知，当温度超过300 ℃时，破坏类型由类型6逐渐向类型4过渡。当温度超过400 ℃时，钢材的屈服强度降低，因此在相同的冲击载荷作用下，钢材的软化导致网壳结构破坏后继续发生倒塌。

3 结 论

对K8型单层球面网壳在火灾和冲击载荷共同作用下的动力响应进行分析，以高大空间火灾升温曲线为基础，建立火灾和冲击载荷耦合作用下的数值模拟计算模型，对高温和冲击载荷共同作用下网壳结构的全过程动力响应进行模拟分析，结论如下。

（1）在本文火源模型下，网壳变形主要以热膨胀为主，网壳结构并没有破坏，网壳节点位移随着温度升高迅速增大，顶点处位移值最大，且离火源水平距离越近，网壳温度增长越快、温度梯度越大。

（2）根据冲击载荷作用下网壳结构的塑性变形和竖向位移情况，将网壳结构的破坏类型分为6种，给出温度为20、100、300和600 ℃时的网壳失效模式分布。因为高温作用下钢材屈服强度和弹性模量同时降低，以及温度对应变率效应的影响，所以冲量较大时网壳结构发生剪切破坏。网壳整体倒塌破坏一般出现在低速大质量冲击情况，冲击未能使网壳立即发生穿透破坏，但网壳出现变形，随着变形不断发展，冲击物不断对网壳施加冲量，直至网壳发生整体倒塌。

参考文献：

[1]

刘晓， 罗永峰. 复杂大跨空间钢结构非线性有限元稳定分析[J]. 计算机辅助工程， 2007， 16（3）： 2529. DOI： 10.3969/j.issn.10060871.2007.03.007.

[2] 赵宪忠， 闫伸， 陈以一. 空间网格结构连续性倒塌试验研究[J]. 建筑结构学报， 2016， 37（6）： 18. DOI： 10.14006/j.jzjgxb.2016.06.001.

[3] ZHAO X Z， YAN S， CHEN Y Y. Comparison of progressive collapse resistance of singlelayer latticed domes under different loadings[J]. Journal of Constructional Steel Research， 2017， 129： 204214. DOI： 10.1016/j.jcsr.2016.11.012.

[4] 丁阳， 齐麟， 李忠献. 应用于单层网壳结构动力响应精细化模拟的杆件计算模型[J]. 建筑结构学报， 2011， 32（5）： 8591. DOI： 10.14006/j.jzjgxb.2011.05.012.

[5] 史建勇， 赵金城. 复杂空间钢结构整体性防火分析的系统方法研究[J]. 土木工程学报， 2008， 41（11）： 5162. DOI： 10.3321/j.issn：1000131X.2008.11.009.

[6] 薛素铎， 邱林波， 冯淼. 空间结构抗火性能研究进展[J]. 建筑钢结构进展， 2009， 11（3）： 2936.

[7] 杜咏， 李国强. 基于场模型的大空间建筑火灾钢构件升温的简化计算方法[J]. 消防科学与技术， 2006， 25（3）： 299303. DOI： 10.3969/j.issn.10090029.2006.03.001.

[8] 贺拥军， 周冬星， 周绪红. 单层球面网壳火灾爆炸动力响应[J]. 土木建筑与环境工程， 2018， 40（1）： 5561. DOI： 10.11835/j.issn.16744764.2018.01.008.

[9] FRIEDMAN R. Quantification of threat from a rapidly growing fire in terms of relative material properties[J]. Fire and Materials， 1978， 2（1）： 2733. DOI： 10.1002/fam.810020108.

[10] NELSON H E. An engineering analysis of early stages of fire development： Fire at Dupont Plaza Hotel and Casino  December 31， 1986： NBSIR 873560[R/OL]. （20181110）[20201010]. https：//www.nist.gov/publications/engineeringanalysisearlystagesfiredevelopmentfiredupontplazahotelandcasino. DOI： 10.6028/NBS.IR.873560.

[11] 王多智， 范峰， 支旭东， 等. 考虑重力效应的单层球面网壳抗冲击载荷性能研究[J]. 哈尔滨工业大学学报， 2009， 41（8）： 1923.

[12] FAN F， WANG D Z， ZHI X D， et al. Failure modes for singlelayer reticulated domes under impact loads[J]. Transactions of Tianjin University， 2008， 14： 545550. DOI： 10.1007/s1220900800947.

[13] 李國强， 杜咏. 实用大空间建筑火灾空气升温经验公式[J]. 消防科学与技术， 2005， 24（3）： 283287. DOI： 10.3969/j.issn.10090029.2005.03.006.

[14] Eurocode 3： Design of steel structures： Part 12： General rules： Structural fire design： BS EN 199312： 2005[S].

[15] XI F， LI Q M， TAN Y H. Dynamic response and critical temperature of a steel beam subjected to fire and subsequent impulsive loading[J]. Computers & Structures， 2014， 135： 100108. DOI： 10.1016/j.compstruc.2014.01.014.

（编辑 武晓英）