某型装甲车制动器热应力磨损耦合仿真分析

摘要: 为提高鼓式制动器在热应力耦合影响下磨损计算的准确性,考虑实际制动过程中温度升高对制动器性能的影响,通过增加温度与磨损率的变化关系修正传统Archard磨损模型,对某型装甲车鼓式制动器进行仿真计算。分析结果表明,在热应力有限元迭代求解过程中,采用完全耦合法持续更新制动器磨损面的几何形状可以不断地修正热应力的计算结果,因此能更真实地描述制动过程中热应力磨损的复杂耦合现象。仿真得到制动器在4种典型工况下的磨损规律,为制动器的优化设计提供依据。
关键词: 鼓式制动器;热应力磨损耦合;完全耦合法;有限元
Abstract: To improve the accuracy of wear calculation of drum brake under the influence of thermalstress coupling, the influence of the temperature rise on brake capacity in the actual braking process is considered, and the traditional Archard wear model is modified by adding the relationship of temperature and wear rate, and then the drum brake of an armored vehicle is simulated. The results show that the thermalstress calculation results can be updated continuously while the full coupling method is used to continuously update the geometry of the brake wear surface in the process of thermalstress finite element iterative solution, and it can more truly describe the complex coupling phenomenon of thermalstresswear in braking process. The wear laws of the brake under 4 typical working conditions are obtained by simulation, which provides the basis for the optimal design of the brake.
Key words: drum brake;thermalstresswear coupling;full coupling method;finite element
0 引 言
在装甲车制动过程中,制动器负载大、工作环境严苛,因此磨损情况十分严重,对其耐磨性设计要求很高。为提高装甲车制动器的耐磨性,需要分析制动器热应力分布情况和预测磨损规律,并且研究制动器磨损的数值仿真方法,为优化制动系统和设计控制策略提供参考。
国内外诸多学者采用有限元法研究车辆制动过程中的多场耦合问题。FUAD等[1]根据鼓式制动器的二維轴对称有限元模型分析制动过程中应力场和温度场的相互作用规律。杨兆军等[2]通过非线性接触分析和瞬态热分析探讨制动鼓的应力和温度分布问题。这些研究均采用简化的模型和热边界条件,未考虑磨损的影响。根据Archard磨损理论,HEGADEKATTE等[3]和李乃斌等[4]对二维和三维滑动磨损以及制动器的磨损进行研究,但没有考虑温度的影响。目前,相关研究主要针对热应力或应力磨损两两耦合问题,而在实际制动过程中,热、应力和磨损三者之间存在复杂的耦合关系。在制动过程中,摩擦力做功生热导致接触面产生热变形,从而改变接触面形态、影响接触应力分布,导致热流密度重新分配和温度场变化。同时,制动瓦接触面的硬度和摩擦因数随温度升高发生变化。针对这一问题,张方宇等[5]和曹文翰等[6]利用顺序耦合法分析热应力磨损耦合问题。顺序耦合法计算效率高,但只考虑温度变化对磨损的单向影响,存在精度损失等问题。张方宇等[7]基于完全耦合分析方法模拟鼓式制动器的热应力磨损耦合过程,但其采用的磨损模型未考虑温度对材料硬度和磨损因数的影响,导致精度损失。
装甲车制动器的工作环境更恶劣,对耐高温性、耐磨性要求更高,需要更精确地模拟制动时热应力磨损的耦合行为。因此,本文基于Abaqus软件求解器提出完全耦合数值计算方法,考虑温度对磨损因数的影响并修正Archard磨损模型,通过热分析对接触面几何形状进行实时更新,更真实地描述制动过程中的热应力磨损耦合行为。采用该方法对某型装甲车鼓式制动器在4种典型工况下的制动过程进行模拟,分析各工况的磨损规律。
1 有限元模型
1.1 几何模型和网格划分
某型装甲车鼓式制动器的主要结构由制动鼓和多个制动瓦组成。
划分网格时,对模型中倒角、螺孔等部位进行简化,可以在不影响计算精度的前提下提高计算效率。因为各制动瓦的磨损情况相似,所以只需要研究其中单个制动瓦与制动鼓的磨损过程。
鼓式制动器模型简化过程见图1。
制动鼓和制动瓦采用热应力耦合分析的实体单元C3D8T模拟:制动鼓平均单元尺寸为9.6 mm,共包含3 450个节点、1 840个单元;制动瓦平均单元尺寸为5.5 mm,共包含3 930个节点、2 092个单元;轴向单元沿轴线对称分布。制动器有限元模型网格见图2。
1.2 材料参数
制动鼓的材料为铸钢12CrNi3,其热导率为71 W/(m·K),密度为7 228 kg/m3,泊松比为0.24,热力学参数见表1。制动瓦为铁基粉末冶金材料,比热容为1 465 J/(kg·K),热导率为60 W/(m·K),弹性模量为140 GPa,密度为2 595 kg/m3,泊松比为0.29,其膨胀系数见表2。
1.3 载荷和边界条件
在极端工况下,按照最高车速70 km/h计算制动器承受的载荷。当主动轮直径为0.616 m时,制动鼓等效转速为61.98 rad/s,制动瓦制动时背面承受制动压力为0.481 MPa。对有限元模型设置接触条件和边界条件并施加载荷。
(1)制动鼓内表面通过刚体约束使与其轴线中心参考点连接,只释放绕其轴线的转动自由度。
(2)制动瓦只能沿制动鼓径向移动,约束其余方向自由度。对制动瓦和制动鼓添加接触对,接触算法为罚函数法,摩擦因数取0.27。制动鼓外表面为主面,制动瓦内表面为从面。
(3)分别对制动瓦背面和制动鼓内、外表面添加对流散热边界条件,设定环境初始温度为293.15 K(常温20 ℃)。
(4)设置制动瓦接触表面为ALE网格作用域。
2 热应力磨损耦合分析
2.1 热应力耦合分析
式中:p为接触压力;q=μpvr,μ为摩擦因数,vr为相对滑移速度;Pq(q,p)为摩擦引起的节点温度载荷向量,体现应力和磨损对温度的影响;PH为边界散热引起的节点温度载荷向量。
式中:Ku为节点位移对节点力的贡献矩阵;u为节点位移向量;KT为温度对节点力的贡献矩阵;Fu为节点力向量。联立式(2)和(3)可以计算得到热应力耦合的有限元公式为
2.2 修正的Archard磨损模型
材料的磨损受许多因素的影响,Archard磨损模型体现接触压力、滑移速度和材料特性与磨损的关系。由于Archard磨损模型列式简单、预测精度能满足大部分工程应用需求,所以在有限元模拟磨损时通常将其作为主要依据,即
式中:V为材料磨损体积;s为滑移距离;k为磨损因数;H为接触面材料的布氏硬度;Fn为接触面受到的法向力。将式(5)两边同时除以接触面积,再对时间求导可得
式中:θ·为磨损率。考虑热效应对磨损的影响时,根据文献[8]和[9]中硬度和磨损因数与温度的函数关系,可以将H和k推广为随摩擦温度变化的回归模型,其表达式为
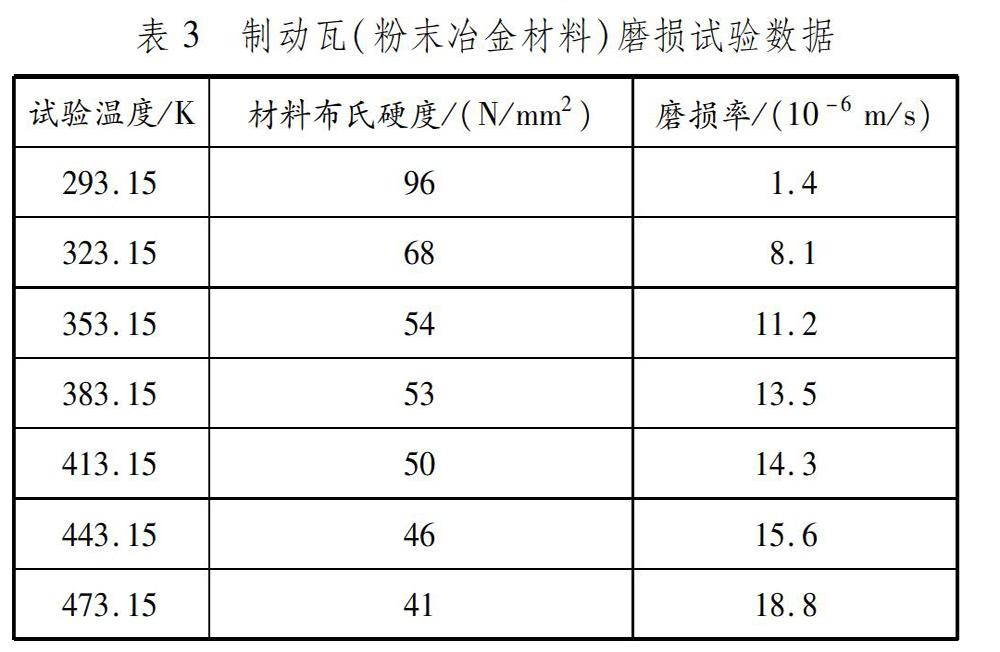
式中:α0、α1、β0、β1、ε为回归系数;T为温度。根据实际试验,得到粉末冶金材料磨损数据,见表3。
2.3 热应力磨损完全耦合分析
在有限元求解时,采用完全耦合法解决制动过程中的热应力磨损耦合问题。将时域离散为N个增量步,每个增量步中先进行热应力耦合分析,输出当前的温度场、应力场和接触节点滑移率等信息,编写UMESHMOTION子程序并求解接触节点的磨损率和磨损方向,通过施加自适应网格约束的方式更新磨损面的有限元几何模型,其分析流程见图4。热应力磨损完全耦合分析基于有限元软件Abaqus,其中:热应力耦合分析采用隐式Coupled tempdisplacement程序;磨损耦合分析采用显式欧拉算法,利用ALE网格和UMESHMOTION子程序实现,设置磨损率为自适应网格的速度约束。
在计算磨损率时,假设在第j个时间增量Δtj内,编号为i的节点磨损率θ·i,j恒定不变,则磨损增量为Δθi,j=θ·i,jΔtj。因此,N个增量步后节点i的累积磨损为
计算磨损方向时,接触平面内节点的磨损方向可以直接设置为施加节点所在平面平均外法向的反方向,但处于几何边角的节点(见图5)同时从属于多个平面,节点的平均外法向方向不可控。
由此可知,为确定某边角节点a的磨损方向,需要指定一个对应的沿着几何边缘的节点b,通过2个点的全局坐标计算磨损向量,再将其映射到节点a的局部坐标系中,从而完成磨损方向的设置。
3 典型工况模拟与结果分析
制动器的磨损主要集中在制动瓦接触面上,制动鼓的磨损可忽略不计。制动瓦与制动鼓的接触表面需经历长时间的磨合才能进入稳定磨损状态,磨合前、后的截面形状对比见图6。由于磨合期状态多变,且制动器主要在磨合后的状态下工作,因此在仿真分析时直接采用制动瓦磨合后的形状。
装甲车在极端工况条件下会出现油门和制动同时作用或连续制动等情况,因此分别针对4种典型工况进行研究。工况1为常温293.15 K时单次减速制动,制动鼓初始转速为61.98 rad/s,减速制动4 s后停止,模拟制动器一般制动工况。工况2为常温293.15 K时恒速制动,制动鼓在制动过程中保持最高转速61.98 rad/s,模拟制动器刚开始工作时油门和制动同时作用的工况。工况3为高温393.15 K时恒速制动,制动鼓在制动过程中保持最高转速61.98 rad/s,模拟制动器工作一段时间后油门和制动同时作用的工况。工况4为常温293.15 K时循环变速制动,制动鼓初始转速为61.98 rad/s,按减速、加速、匀速各2 s的循环周期进行总时长为30 s的变速制动,模拟制动器连续制动工况。
在制动瓦接触面上取5个采样点(见图7),分析制动器在4种工况下的磨损规律。制动瓦相对制动鼓的运动方向为由采样点2到采样点4,因此称采样点2为前、采样点4为后。
由于摩擦力不稳定,制动过程中出现摩擦震颤问题。当节点处于接触开与合的交替状态时,采样点的磨损率并非光滑曲线,因此采用最大包络线绘制磨损率的变化曲线,并对比各采样点在4种典型工况下的磨损率变化规律。为考察修正Archard磨损模型中温度效应的影响,计算工况2时采样点1和2分别基于传统Archard模型和修正Archard模型的磨损率变化情况,见图8。传统Archard模型中的磨损因数k为常数,磨损率的变化不受温度影响,当转速和压力趋于稳定时,磨损率趋于恒定常数。修正Archard模型考虑温度效应的耦合,磨损率随着温度上升而增大。
根据式(9)和(10),通过粉末冶金磨损试验得到的硬度和磨损因数与温度的關系,开展4种典型工况的仿真计算。工况1各采样点的磨损率变化曲线见图9,在转速逐渐降低为0的过程中,磨损率先增大再减小,最终降为0,体现磨损率与转速相关的特点。由于制动鼓为凸形外轮廓,制动瓦接触面中部(采样点2、3、4)的接触应力比两侧(采样点1、5)大,所以中部的磨损率也大于两侧。此外,由于制动瓦上接触应力的前后分布不对称,制动瓦前部受到后部抵制变形的挤压,接触应力更大,所以前部采样点2的磨损率最高,体现磨损率与接触应力相关的特点。制动瓦两侧对称,其接触状态和磨损规律基本一致。
工况2各采样点的磨损率和温度变化曲线分别见图10和11,制动瓦中部的磨损率先增大后逐渐趋于稳定,两侧的磨损率持续增大。磨损改变接触面的几何形态,并且间接影响接触应力的分布,因此制动瓦接触面上各位置的磨损率不同。由于几何形态的变化,磨损量大的区域接触应力逐渐减小,所以磨损率也减小并趋于稳定,如采样点2。在磨损量小的区域,磨损率随着接触应力增大而持续增大。
工况3各采样点的磨损率变化曲线见图12。工况3制动瓦的磨损规律与工况2类似,但由于温度影响,高温导致更高的磨损率,接触面几何形貌的变化导致接触应力的减小更加明显,所以制动瓦中部区域的磨损率先降低后趋于稳定。随着制动瓦两侧接触应力持续增大,磨损率也持续增大。工况3制动瓦温度升高主要集中在前部,变化规律与工况2类似,见图13和14。
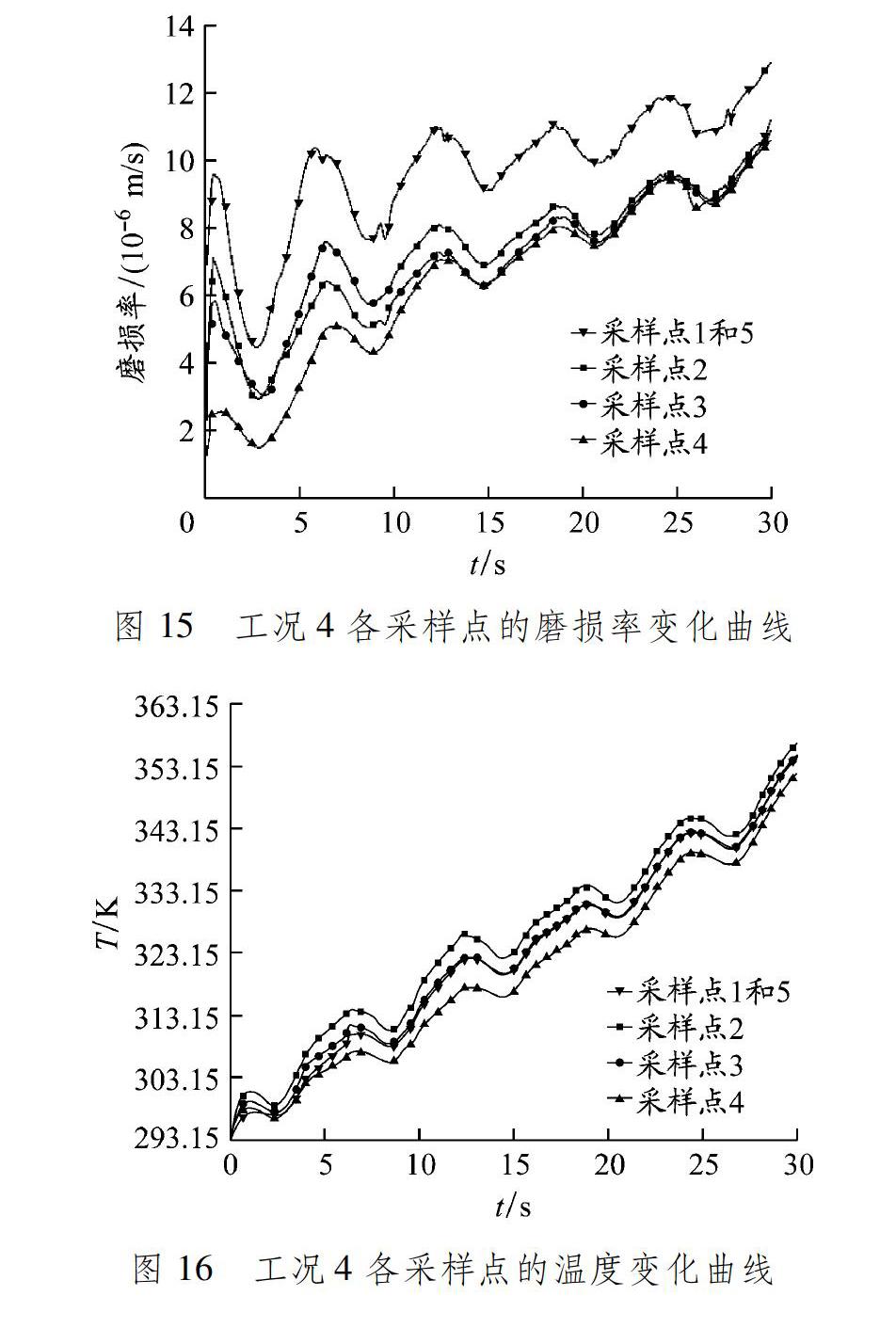
工况4各采样点的磨损率和温度变化曲线分别见图15和16。由此可知:转速变化导致磨损率曲线发生周期性波动,且随着时间的推移,磨损率的增长整体趋于平稳;接触面内各采样点的磨损率和温度从初始较大的差异到逐渐趋于重合,说明在磨损导致几何变形的影响下接触面内的接触应力和温度有均匀化的趋势。
4 结术语
本文研究某型装甲车制动器磨损的数值仿真方法,通过修正Archard磨损模型,考虑在磨损过程中温度效应的影响,采用完全耦合法对制动过程进行数值仿真。研究结果表明,基于修正Archard模型的完全耦合法可以有效地模拟热应力磨损的复杂耦合过程。分析得到4种典型工况下温度、接触应力和磨损率的变化规律与分布特点,可用于对制动器耐磨性能和寿命的评估,为制动器的结构优化设计提供理论依据。
参考文献:
[1] FUAD K, DAIMARUYA M, KOBAYASHI H. Temperature and thermal stresses in a brake drum subjected to cyclic heating[J]. Journal of Thermal Stresses, 1994, 17(4): 515527.
[2] 杨兆军, 范久臣, 丁树伟, 等. 鼓式制动器应力场数值模拟[J]. 电子科技大学学报, 2010, 39(4): 623628. DOI: 10.3969/j.issn.10010548.2010.04.032.
[3] HEGADEKATTE V, HUBER N, KRAFT O. Finite element based simulation of dry sliding wear[J]. Modelling and Simulation in Materials Science and Engineering, 2005, 13(1): 5775.
[4] 李乃斌, 李耀平. 基于Ansys Workbench鼓式制动器制动鼓的有限元分析[J]. 价值工程, 2017, 36(8): 9193. DOI: 10.14018/j.cnki.cn131085/n.2017.08.036.
[5] 張方宇, 桂良进, 范子杰. 销盘试验的热应力磨损耦合模拟研究[J]. 机械工程学报, 2015, 51(8): 107115. DOI: 10.3901/JME.2015.08.107.

