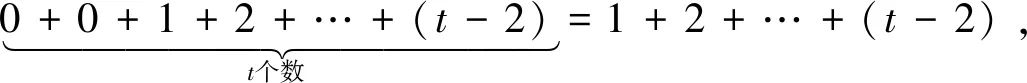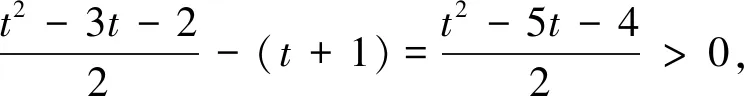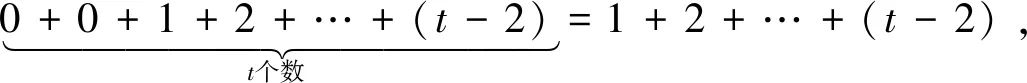包含广义Euler函数φ2(m)的一方程的正整数解
张四保,姜莲霞
(喀什大学 数学与统计学院, 新疆 喀什 844008)
0 引言
Euler函数φ(m)是数论中的一个极为重要的函数,对于Euler函数φ(m)的性质以及包含Euler函数φ(m)的方程是内容极为丰富的研究课题,其有着大量的研究成果。文献[1]讨论了方程φ(n)=2ω(n)3ω(n)5ω(n)的可解性,给出了其正整数解的情况;文献[2]讨论了方程φ[φ(x)]=2t的可解性;文献[3]讨论了方程φ(m)=2Ω(m)+ω(m)3Ω(m)+ω(m)与φ(m)=2Ω(m)-ω(m)3Ω(m)-ω(m)的可解性,给出这两个方程的正整数解的情况;文献[4]利用初等方法给出方程φ[φ(n)]=2Ω(n)的所有正整数解;文献[5]基于整数的分解给出了方程φ(n)=2Ω(n)3Ω(n)的正整数解;文献[6]给出了方程φ{φ[φ(n)]}=2ω(n)的所有正整数解。
为将Lehmer同余式的模从素数的平方推广到任意正整数的平方,CAI等[7]引入了广义Euler函数φe(n),其中e为正整数。对于包含广义Euler函数φe(n)的方程的可解性问题也有着丰富的研究内容。文献[8]讨论了方程φe(n)=2tω(n)的可解性,给出了其部分正整数解,其中e=2,3,4,6;文献[9]讨论了方程φ2(n)=2ω(n)与方程φ2[φ2(n)]=2ω(n)的可解性,获得了这2个方程的所有正整数解;文献[10]利用初等方法及广义Euler函数φ2(m)的性质给出了方程φ2(m)=2ω(m)3ω(m)的一切正整数解。笔者将利用函数φ2(m)的性质以及分类分段的讨论方式来讨论方程式(1)的可解性问题,给出该方程的正整数解的情况。
φ2(m)=2ω(m)3Ω(m),
(1)
式中函数Ω(m)均为正整数m的质因子个数函数,函数ω(m)均为正整数m的互异质因子个数函数。
1 主要结论及其证明
定理1方程式(1)有正整数解m=13, 91, 95, 111, 146, 436, 665, 741, 777, 962, 1 022, 1 090, 1 304, 2 812, 3 052, 3 260, 5 187, 6 734, 7 030, 7 630, 8 322, 8 502, 9 128, 11 688, 19 684, 22 820, 24 852,25 428,29 220, 49 210, 62 130, 63 570, 74 328, 81 816, 177 996, 185 820, 204 540, 520 296, 434 910, 1 300 740, 3α×37, 3α×247, 3α×259, 3α×1 729, 3α×2 834, 3α×3 896, 3α×8 284, 3α×8 476, 3α×9 740, 3α×19 418, 3α×19 838, 3α×20 710, 3α×21 190, 3α×24 776, 3α×27 272, 3α×59 332, 3α×61 940, 3α×68 180, 3α×144 970, 3α×173 432, 3α×433 580,其中α≥2,为整数。证明显然m=1,2不是方程式(1)的正整数解,则m≥3,可分m为单数与m为双数的情况进行讨论。
情况1当m为单数,此时设m=q1α1q2a2…qtαt≥3是m的标准分解式,其中q1 (2) 即有 q1α1-1(q1-1)q2α2-1(q2-1)…qtαt-1(qt-1)=2t+1×3α1+α2+…+αt。 (3) 在式(3)的右端只有唯一的单因数3,则指数α1,α2,…,αt中只能有1个可以满足αi≥2,1≤i≤t。因q1 (q1-1)(q2-1)…(qt-1)=2t+1×3t, (4) 而当t≥2,且α=α1≥2时,由式(3)有 (q2-1)…(qt-1)=2t×3t。 (5) ① 当t=1时,有: 当α1=1时,由式(4)有q1-1=22×3,则q1=13,因而此时m=13是方程(1)的1个解。当α1≥2时,由式(3)有q1α1-1(q1-1)=22×3α1,此时无单质数解。 ② 当t=2时,有: 当α1=α2=1时,由式(4)有(q1-1)(q2-1)=23×32,因而有q1=3,q2=37或q1=5,q2=19或q1=7,q2=13,因而此时方程(1)有3个解m=3×37=111,m=5×19=95,m=7×13=91。 当α=α1≥2时,由式(5)有q2-1=22×32,则q2=22×32+1=37,则此时方程(1)有解m=3α×37,其中α≥2为整数。 ③ 当t=3时,有:当α1=α2=α3=1时,由式(4)有(q1-1)(q2-1)(q3-1)=24×33,因而有q1=3,q2=7,q3=37或q1=3,q2=13,q3=19或q1=5,q2=7,q3=19,因而此时方程(1)有3个解m=3×7×37=777,m=3×13×19=741,m=5×7×19=665。 当α=α1≥2时,由式(5)有(q2-1)(q3-1)=23×33,则有q2=7,q3=37或q2=13,q3=19,因而此时方程(1)有2个解m=3α×7×37=3α×259,m=3α×13×19=3α×247,其中α≥2为整数。 ④ 当t=4时,有: 当α1=α2=α3=α4=1时,由式(4)有(q1-1)(q2-1)(q3-1)(q4-1)=25×34,因而有q1=3,q2=7,q3=13,q4=19,因而此时方程(1)有解m=3×7×13×19=5 187。 当α=α1≥2时,由式(5)有(q2-1)(q3-1)(q4-1)=24×34,则有q2=7,q3=13,q4=19,因而此时方程(1)有解m=3α×7×13×19=3α×1 729,其中α≥2为整数。 ⑤ 当t≥5时,有: 情况2当m为双数,此时设m=2βq1α1q2a2…qtαt>3是m的标准分解式,其中q1 (6) 即有2β-1q1α1-1(q1-1)q2α2-1(q2-1)…qtαt-1(qt-1)=2t+2×3β+α1+α2+…+αt。同m为单数时的讨论可知,只可能有α=α1≥2,而αj=1;j=2,3,…,t,并且此时有q1=3。因而当α1=α2=…=αt=1时,有 (q1-1)(q2-1)…(qt-1)=2t+3-β×3β+t, (7) 而当t≥2,且α=α1≥2时,则有 (q2-1)…(qt-1)=2t+2-β×3β+t。 (8) ① 当t=1时,有: 当α1=1时,由式(7)有q1-1=24-β×3β+1。当β=1时,有q1-1=23×32,则q1=73,则此时方程(1)有解m=2×73=146;当β=2时,有q1-1=22×33,则q1=109,则此时方程(1)有解m=22×109=436;当β=3时,有q1-1=2×34,则q1=163,则此时方程(1)有解m=23×163=1 304;当β≥4时,方程(1)无解。当α=α1≥2时,有2β×3α-1=23×3β+α,不可能,故此时方程(1)无解。 ② 当t=2时,有: 当α1=α2=1时,由式(7)有(q1-1)(q2-1)=25-β×3β+2。当β=1时,有(q1-1)(q2-1)=24×33,则q1=5,q2=109或q1=7,q2=73或q1=13,q2=37,则此时方程(1)有3个解m=2×5×109=1 090,m=2×7×73=1 022,m=2×13×37=962;当β=2时,有(q1-1)(q2-1)=23×34,则q1=5,q2=163或q1=7,q2=109或q1=19,q2=37,则此时方程(1)有3个解m=22×5×163=3 260,m=22×7×109=3 052,m=22×19×37=2 812;当β=3时,有(q1-1)(q2-1)=22×35,则q1=3,q2=487或q1=7,q2=163,则此时方程(1)有2个解m=23×3×487=11 688,m=23×7×163=9 128;当β≥4时,方程(1)无解。 当α=α1≥2时,由式(8)有q2-1=24-β×3β+2,则当β=1时,有q2=217非质数,此时方程(1)无解;当β=2,有q2=325非质数,此时方程(1)无解;当β=3,有q2=487,此时方程(1)有解m=23×3α×487=3α×3 896,其中α≥2为整数;当β≥4时,方程(1)无解。 ③ 当t=3时,有: 当α1=α2=α3=1时,由式(7)有(q1-1)(q2-1)(q3-1)=26-β×3β+3。当β=1时,有(q1-1)(q2-1)(q3-1)=25×34,则q1=3,q2=13,q3=109或q1=3,q2=19,q3=73或q1=5,q2=7,q3=109或q1=5,q2=19,q3=37或q1=7,q2=13,q3=37,则此时方程(1)有5个解m=2×3×13×109=8 502,m=2×3×19×73=8 322,m=2×5×7×109=7 630,m=2×5×19×37=7 030,m=2×7×13×37=6 734;当β=2时,有(q1-1)(q2-1)(q3-1)=24×35,则q1=3,q2=5,q3=487或q1=3,q2=13,q3=163或q1=3,q2=19,q3=109或q1=5,q2=7,q3=163或q1=7,q2=19,q3=37,则此时方程(1)有5个解m=22×3×5×487=29 220,m=22×3×13×163=25 428,m=22×3×19×109=24 852,m=22×5×7×163=22 820,m=22×7×19×37=19 684;当β=3时,有(q1-1)(q2-1)(q3-1)=23×36,则q1=3,q2=7,q3=487或q1=3,q2=19,q3=163,则此时方程(1)有2个解m=23×3×7×487=81 816,m=23×3×19×163=74 328;当β≥4时,方程(1)无解。 当α=α1≥2时,由式(8)有(q2-1)(q3-1)=25-β×3β+3,则当β=1时,有q2=13,q3=109,此时方程(1)有解m=2×3α×13×109=3α×2 834,其中α≥2为整数;当β=2时,有q2=5,q3=487或q2=13,q3=163或q2=19,q3=109,此时方程(1)有3个解m=22×3α×5×487=3α×9 740,m=22×3α×13×163=3α×8 476,m=22×3α×19×109=3α×8 284,其中α≥2为整数;当β=3时,有q2=7,q3=487或q2=19,q3=163,此时方程(1)有2个解m=23×3α×7×487=3α×27 272,m=23×3α×19×163=3α×24 776,其中α≥2为整数;当β≥4时,方程(1)无解。 ④ 当t=4时,有: 当α1=α2=α3=α4=1时,由式(7)有(q1-1)(q2-1)(q3-1)(q4-1)=27-β×3β+4。当β=1时,有(q1-1)(q2-1)(q3-1)(q4-1)=26×35,则q1=3,q2=5,q3=13,q4=163或q1=3,q2=5,q3=19,q4=109或q1=5,q2=7,q3=19,q4=37,则此时方程(1)有3个解m=2×3×5×13×163=63 570,m=2×3×5×19×109=62 130,m=2×5×7×19×37=49 210;当β=2时,有(q1-1)(q2-1)(q3-1)(q4-1)=25×36,则q1=3,q2=5,q3=7,q4=487或q1=3,q2=5,q3=19,q4=163或q1=3,q2=7,q3=13,q4=163,则此时方程(1)有3个解m=22×3×5×7×487=204 540,m=22×3×5×19×163=185 820,m=22×3×7×13×163=177 996;当β=3时,有(q1-1)(q2-1)(q3-1)(q4-1)=24×37,则q1=3,q2=7,q3=19,q4=163,方程(1)有1个解m=23×3×7×19×163=520 296;当β≥4时,方程(1)无解。 当α=α1≥2时,由式(8)有(q2-1)(q3-1)(q4-1)=26-β×3β+4,则当β=1时,有q2=5,q3=13,q4=163或q2=5,q3=19,q4=109或q2=7,q3=13,q4=109或q2=7,q3=19,q4=73,此时方程(1)有4个解m=2×3α×5×13×163=3α×21 190,m=2×3α×5×19×109=3α×20 710,m=2×3α×7×13×109=3α×19 838,m=2×3α×7×19×73=3α×19 418,其中α≥2为整数;当β=2时,有q2=5,q3=7,q4=487或q2=5,q3=19,q4=163或q2=7,q3=13,q4=163,此时方程(1)有3个解m=22×3α×5×7×487=3α×68 180,m=22×3α×5×19×163=3α×61 940,m=22×3α×7×13×163=3α×59 332,其中α≥2为整数;当β=3时,有q2=7,q3=19,q4=163,此时方程(1)有解m=23×3α×7×19×163=3α×173 432,其中α≥2为整数;当β≥4时,方程(1)无解。 ⑤ 当t=5时,有: 当α1=α2=α3=α4=α5=1时,由式(7)有(q1-1)(q2-1)(q3-1)(q4-1)(q5-1)=28-β×3β+5。当β=1时,有(q1-1)(q2-1)(q3-1)(q4-1)(q5-1)=27×36,则q1=3,q2=5,q3=7,q4=19,q5=109,则此时方程(1)有解m=2×3×5×7×19×109=434 910;当β=2时,有(q1-1)(q2-1)(q3-1)(q4-1)(q5-1)=26×37,则q1=3,q2=5,q3=7,q4=19,q5=163,则此时方程(1)有解m=22×3×5×7×19×163=1 300 740;当β=3时,有(q1-1)(q2-1)(q3-1)(q4-1)(q5-1)=25×38无互异的单质数解,则此时方程(1)无解;当β≥4时,方程(1)无解。 当α=α1≥2时,由式(8)有(q2-1)(q3-1)(q4-1)(q5-1)=27-β×3β+5,则当β=1时,有q2=5,q3=7,q4=19,q5=109,则此时方程(1)有解m=2×3α×5×7×19×109=3α×144 970,其中α≥2为整数;当β=2时,有q2=5,q3=7,q4=19,q5=163,则此时方程(1)有解m=22×3α×5×7×19×163=3α×433 580,其中α≥2为整数;当β=3时,此时方程(1)无解;当β≥4时,方程(1)无解。 ⑥ 当t≥6时,有: 综合以上讨论,可得本文定理1的结论。证毕。