不同埋深隧道开挖对地表沉降影响的三维有限元分析
严鹏飞,殷建光,葛新辉,万青青,李宏波*,3,4
(1.宁夏大学 土木与水利工程学院, 宁夏 银川 750021;2.健研检测集团有限公司, 福建 厦门 361026;3.宁夏节水灌溉与水资源调控工程技术研究中心, 宁夏 银川 750021;4.旱区现代农业水资源高效利用教育部工程研究中心, 宁夏 银川 750021)
0 引言
随着社会经济的发展,我国一线城市地上空间急剧缩小,城市交通日益繁重,传统的地面公路已无法满足实际交通的需求,城市地铁应运而生[1-2]。与传统公路隧道相比,地铁隧道具有地质条件复杂、与既有建筑物距离近和下穿人口密集区域的特点[3]。一旦发生塌方事故,将会造成处理困难、工期延误甚至是地面建筑物沉降、倾斜、倒塌和人员伤亡等巨大的损失。如何安全、快速地在城市软弱围岩中进行隧道施工,已成为广大学者和工程人员研究的热门问题[4-6]。
基于隧道开挖后围岩与衬砌的工作特点,研究方法主要有模型试验和数值模拟两种。张成平等[7]通过模型试验,针对软弱围岩深、浅埋隧道两种情况,研究了隧道塌方特征和演化规律,并对塌落拱形状用二次抛物线进行拟合;张新善等[8]利用FLAC3D软件,研究了西安地铁黄土隧道开挖过程中支护时机对隧道内部地表、拱顶和侧墙影响程度,结果表明:对于黄土隧道,开挖初期地应力释放较大,往往引起较大沉降位移,因此必须做好前期的预加固措施。王军祥等[9]利用有限元软件ABAQUS建立隧道三维模型,模拟计算了围岩和衬砌的位移、受力情况。通过方差和极差分析,得到了影响围岩稳定性的重要程度依次为弹性模量、黏聚力、泊松比、内摩擦角和膨胀角。上述研究多针对隧道开挖后围岩的应力和应变方面进行,没有深入对比分析不同隧道埋深对地表沉降的影响规律,也鲜有提及对于不同埋深隧道安全性保证的防控重点。
为此,文章以厦门市东渡路站-建业路站隧道区间为工程背景,采用有限元软件ABAQUS建立不同埋深的三维隧道模型,研究了不同隧道埋深对地表沉降的影响规律,进而提出不同埋深隧道在开挖掘进程中的防控重点,用以指导后续的实际施工。
1 工程概况
东渡路站-建业路站区间属于厦门市轨道交通工程2号线1期工程。区间跨度较大,穿越地层较多,部分区段包括碎裂状强风化花岗岩及残积砂质黏性土,地层变化较大。右线总长1 001.941 m,左线总长987.275 m。轨面标高为-30.141~-11.562 m,区间隧道最大埋深约79.5 m,最小埋深约10.48 m。隧道区间范围内覆盖层从上往下主要分为3层,第1层土主要为杂填土、素填土和填石等;第2层土主要为中沙土、粉质黏土和强风化花岗岩,厚度及性能变化较大;第3层土主要为强风化辉绿岩和中等风化花岗岩。下伏基岩主要为中等风化花岗岩。文章根据实际工程情况和隧道纵断面图选取隧道埋深为4D(D表示隧道开挖直径)的一处断面进行模拟,模型参数根据地勘报告中的工程地质情况进行设置。
2 有限元模型的建立
2.1 计算假定
文章的数值模拟计算基于如下假定:①围岩的初始应力场仅考虑土体自重;②忽略地下水压力的影响;③为了和实际测量数据相对应,仅考虑初期支护C25喷射混凝土;④隧道开挖方法为理想的全断面开挖法。
2.2 建立模型
根据隧道开挖横断面图,确定隧道模型的开挖尺寸。一般情况下,为减小边界对模型的影响,模型宽度取10D,隧道底边至模型底面边界为4D。为方便观察开挖过程中围岩内部的应力应变变化情况,根据对称原则,取一半建立模型。围岩的开挖方法为全断面开挖,初期支护为30 cm厚的C25喷射混凝土。
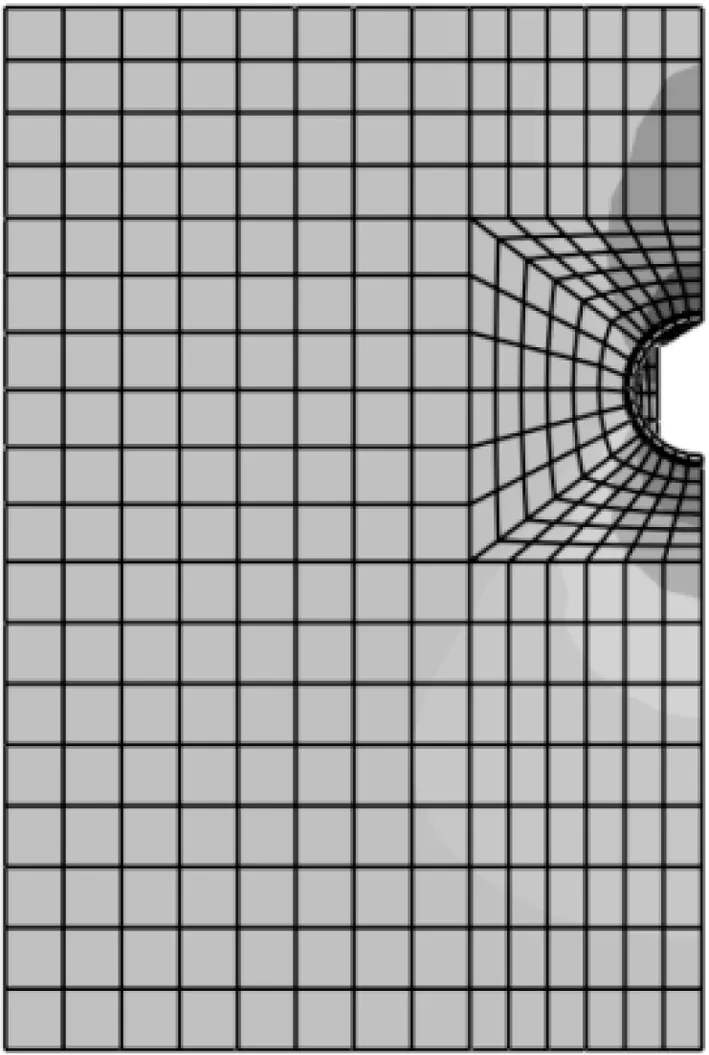
文中地铁隧道区间围岩采用ABAQUS中的线性D-P(drucker-prager)模型,该模型适用于岩石和土壤等颗粒状材料。C25喷射混凝土的本构关系定义为弹性模型。网格划分方法为sweep,为保证开挖部分网格的均匀性,采用中性轴法。衬砌和土体的单元类型为减缩积分实体单元C3D8R,土体和衬砌的网格划分如图1所示。

图1 土体和衬砌网格
2.3 模型参数的计算
Mohr-Coulomb模型与Drucker-Prager的参数并不相等,在三维模型中,它们的参数有如下转换关系[10]:
(1)
(2)
(3)
式中:β是D-P准则屈服面在p-t应力空间上的倾角;c是土体的黏聚力;φ是土体的内摩擦角;σc是单轴抗压强度;k是三轴拉伸强度与压缩强度的比值。
在D-P屈服准则中,为保证屈服面为凸面,k的取值范围为0.778≤k≤1.0。由公式(2)可得
(4)
式(4)表明:φ≤22°,若φ大于22°时,k取0.778;若φ远大于22°,则更适合采用Mohr-Coulomb模型。
土层的分布一般是不均匀的且相互内嵌,如果按照实际情况进行划分,会给数值模拟带来很大的不便,而不会对计算结果的精度带来较大提升,因此需对模型进行一定程度的简化。简化原则是把邻近土体土性较为相似的土层进行合并[11],最终土体的参数取合并土体参数的加权平均值。通过这种计算方法得到简化后土体的弹性模量E、重度γ、内摩擦角φ和黏聚力c等。
2.4 围岩和衬砌材料参数
根据隧道纵断面图,选取4D埋深下的一段隧道区间作为研究对象,通过调整隧道埋深来研究围岩的变形及地表沉降规律。围岩和衬砌基本力学参数见表1。

表1 围岩和衬砌相关参数
2.5 模型荷载、边界条件及接触
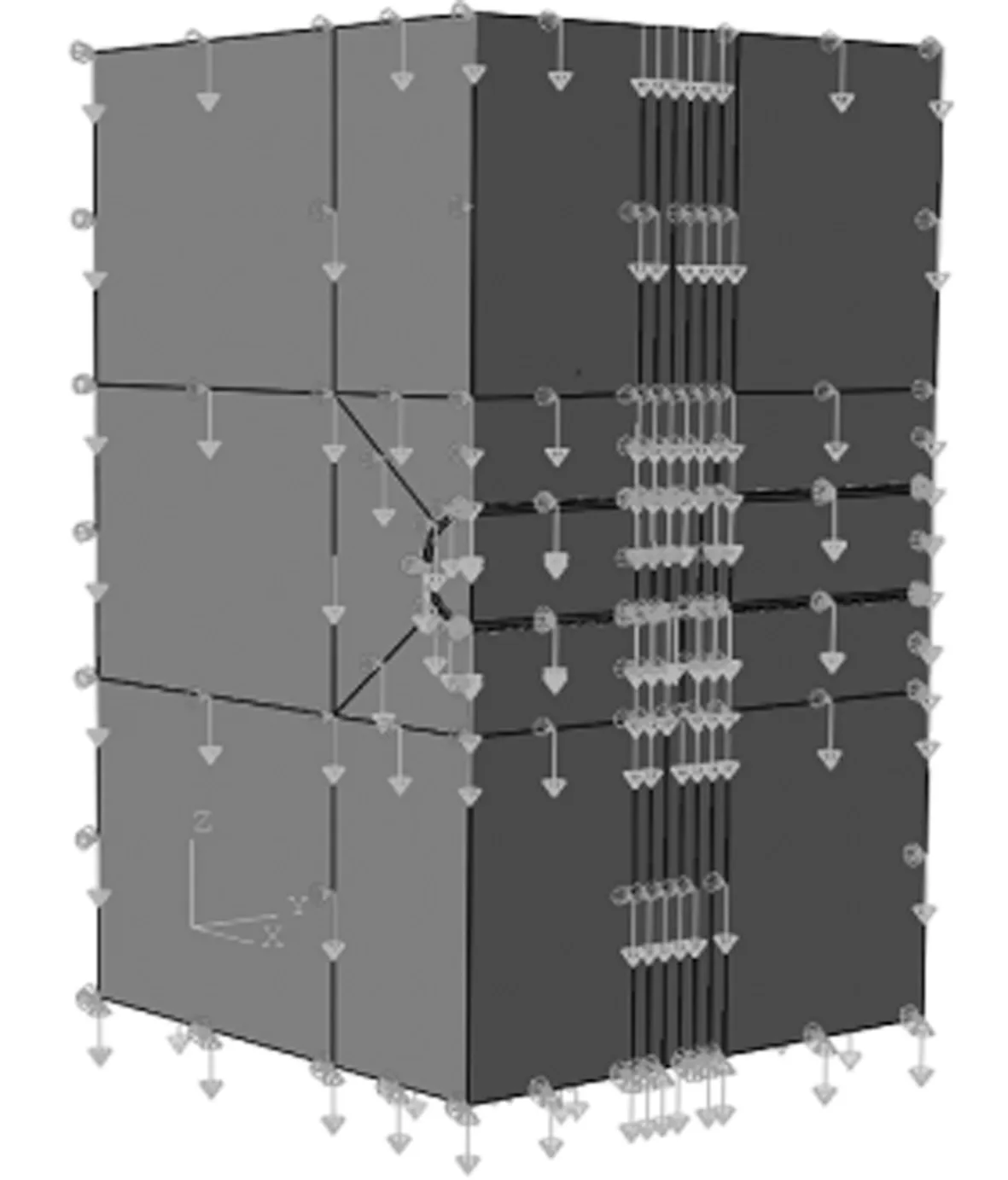
图2 模型的荷载加载情况和边界条件
根据假定条件,给围岩添加重力来模拟围岩的自重应力场。采用软化模量法来模拟开挖过程中地应力的释放现象,通过生死单元功能来控制衬砌的生效时机。衬砌与围岩之间采用tie约束,将围岩作为主面,衬砌为从面。对模型左、右和前、后面分别施加x、y方向上的约束,对底面施加x、y、z方向的约束。模型中荷载的加载情况和边界条件如图2所示。
2.6 计算结果验证
通过对模型进行提交计算,得到4D埋深下的初始地应力平衡如图3所示。根据土体的平均重度和模型的高度进行计算,验证初始地应力平衡状态下模型的正确性。由表1可得土体的平均重度为19.60 kN/m3,模型高度为58 m,通过计算得到模型底面的重力为1.14×106N,根据图3结果可验证初始地应力平衡状态下的模型是正确的。
通过path建立地表路径,用Edit XY Date提取数据,将提取的数据和对应的工程实测数据进行对比,由图4可知,通过ABAQUS模拟计算的4D埋深下的地表沉降值与对应的工程实测值吻合较好,进一步验证了模型的正确性,说明通过ABAQUS模拟的隧道地表沉降在实际工程应用中可以较好地指导施工。
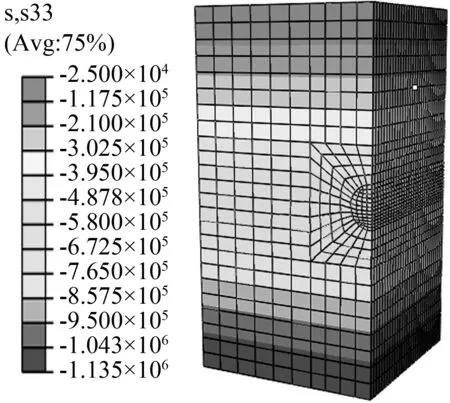
图3 4D埋深下的初始地应力平衡
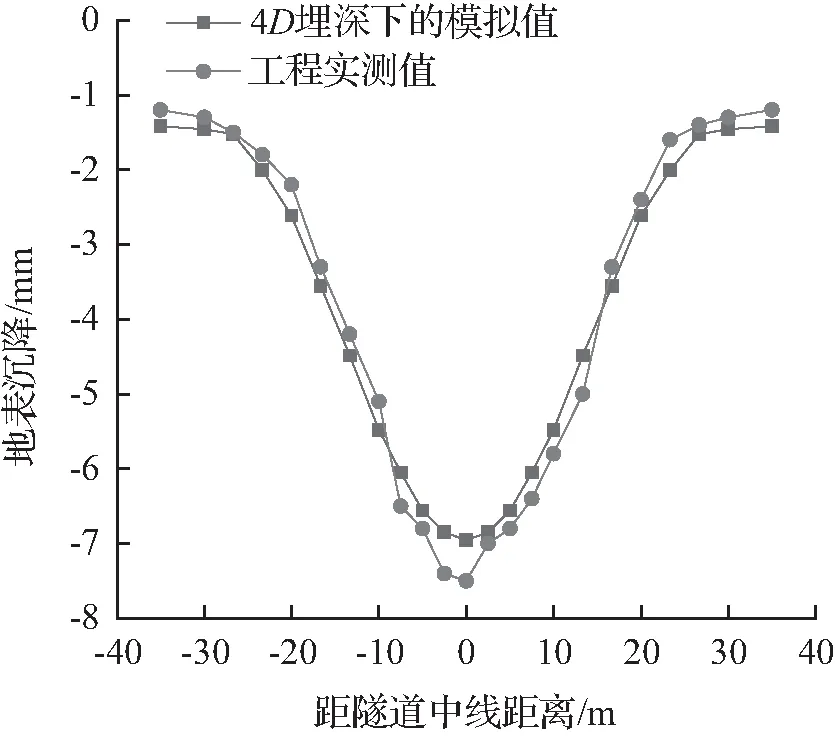
图4 4D埋深下的地表沉降和工程实测值
3 计算结果及分析
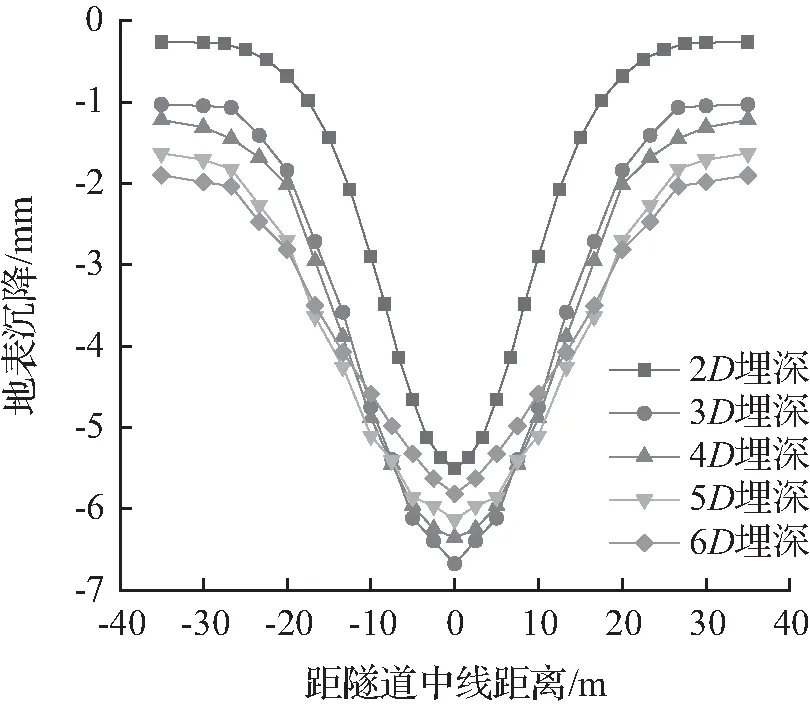
图5 不同埋深隧道的地表沉降
隧道开挖后,围岩应力进行重新分布,从而引起拱顶和地表沉降。引起拱顶和地表沉降的原因比较复杂,如隧道开挖时的开挖方法、围岩参数、隧道跨度、隧道埋深和地下水压力等都会不同程度地引起相应的沉降变形。
考虑隧道埋深对地表沉降的影响,固定隧道底面到模型底边的距离为4D,横向边界宽度保持不变,通过调整隧道顶面到模型顶面的距离,以达到调整隧道埋深的目的。分析结果如图5所示。
不同埋深隧道的地表沉降规律均与Peck曲线[12]规律相似,主要表现为地表沉降的大小和沉降槽宽度。沉降槽宽度公式
(5)
式中:i为沉降槽宽度;φ为土的内摩擦角;Z0为隧道轴线埋深。
由图5可知,当隧道埋深从2D增加到3D时,地表沉降逐渐增大,这是因为当隧道埋深较浅时,围岩的自承能力不能充分发挥。随着隧道埋深的增大,围岩的自重应力和自承能力均会增大,但围岩的自承能力的增长速度小于围岩自重应力的增长速度,最终表现为地表沉降会随着隧道埋深的增大而增大。当隧道埋深从3D增加到6D时,最大地表沉降值反而是减小的,这是由于隧道埋深增长到了一定的程度,土体的自承能力能够充分发挥作用,土体的自承能力的增长速度又反超了自重应力的增加速度,最终表现为地表沉降随着隧道埋深的增加呈现为先增大后减小的趋势。当距隧道中心线距离大于25 m时,沉降槽曲线逐渐趋于平缓,此时隧道开挖对地表沉降的影响逐渐减小。由公式(5)可知,沉降槽宽度和隧道埋深成正比,沉降槽宽度随着隧道埋深的增大而增大,这是因为随着隧道埋深的增大,受隧道开挖影响的土体区域也在不断地增大,如图6所示。
(a) 2D埋深

图7 拱顶地表沉降与隧道埋深关系曲线
隧道拱顶沉降值与埋深的关系如图7所示,随着隧道埋深的增加,土体的自承能力增加速度和围岩自重应力的增加速度相等时,在隧道埋深为3D附近达到了一个平衡点,此时,隧道正拱顶地表沉降值达到最大。平衡点所处的位置与隧道开挖跨度、土体参数和开挖方式等因素有关。当隧道埋深较浅时,平衡拱[13]发展至地表,拱效应不能充分发挥自稳作用,在此阶段,随着隧道埋深的增大地表沉降也在不断地增大。随着隧道埋深的继续增大,平衡拱在围岩土体中完全形成时,拱效应的自承作用明显,在此阶段,地表沉降将会随着埋深的增加而减小。这是因为当隧道埋深较深时,围岩平衡拱的自承作用明显,能够充分发挥作用,故隧道开挖对围岩的扰动较小,引起的地表沉降也较小[14]。地表达到最大沉降值时所对应的隧道埋深,与平衡拱在围岩中充分发挥作用的深度一致,因此,平衡点3D还可作为该工程深埋、浅埋隧道界限的划分参考标准。
4 深埋、浅埋隧道施工时安全性保证的防控要点
本文根据不同埋深隧道的地表沉降规律和平衡拱理论,将3D隧道埋深作为适用于本工程相同围岩参数的深埋、浅埋隧道的划分界限。同等条件下,深埋和浅埋隧道地表沉降的差异性是由覆跨比不同造成的,浅埋隧道的覆跨比小,围岩不能形成稳定的平衡拱,围岩的自承作用不明显。深埋隧道的覆跨比大,围岩可以形成稳定的平衡拱,围岩的自承作用对隧道的稳定性影响较大。基于此,针对以上特点,对深埋、浅埋隧道在设计和开挖掘进中制定合理的防控措施:
① 从安全和经济角度出发,对深埋、浅埋段隧道进行支护参数设计时,要根据相应的地勘报告对具体围岩参数进行分析,根据实际工程情况和覆跨比确定符合实际工程的深埋、浅埋隧道界限划分标准。根据深埋、浅埋隧道的划分标准,针对相同围岩参数不同埋深的隧道区间设计不同的支护参数,充分利用围岩的自稳能力。此外,对于浅埋段上覆建筑物复杂和围岩较差的情况,设计选线时可以倾向考虑隧道埋深较大的,以达到安全和经济效益最大化的目的。
② 对于浅埋隧道,由于围岩不能形成稳定的平衡拱,如果发生塌方事故,易造成塌穿型塌方和明显的地表沉陷。因此,在开挖过程中应充分考虑地表建筑物和其他易对围岩稳定造成影响的不可忽略外在因素。隧道的掘进和支护应严格遵守隧道施工规范,及时进行支护,必要时还应当申请设计变更适当的增大支护参数。
③ 对于深埋隧道,围岩可以形成稳定的平衡拱,相较于浅埋隧道而言,即使发生塌方事故也不会造成塌穿型塌方,但其影响的区域相较于浅埋隧道大。随着循环掘进深度的增加,对上方土体的影响区域会随之增大。因此在实际工程中,要严格控制隧道掘进的安全步距。
5 结论
文章通过有限元模拟软件ABAQUS对厦门市东渡路站-建业路站区隧道区间进行模拟,研究了不同埋深隧道的地表沉降规律。通过对有限元模拟和实测工程值的结果进行分析,得出以下结论:
① 随着隧道埋深的增加,沉降槽宽度也在不断增加,受隧道开挖影响的土体区域不断地增大,而拱顶地表沉降则呈现先增大后减小的规律。
② 距隧道中心线水平距离大于25 m时,沉降槽曲线逐渐趋于平缓,表明相同条件下隧道开挖对距隧道中心线25 m以外的地表沉降影响相对较小。
③ 随着隧道埋深的增加,土体的自承能力增加速度和围岩自重应力的增加速度将会在隧道埋深3D附近达到平衡点,此时,隧道正拱顶地表沉降值达到最大,且平衡点所处的位置与隧道开挖跨度、土体参数和开挖方式等因素有关。
④ 平衡点对应的隧道埋深可作为同等条件下深、浅埋隧道的划分标准。对于本工程而言,与所研究围岩参数较为相似的隧道区间,可以将埋深3D作为深、浅埋隧道的界限划分标准。

