钢管混凝土拱桥大型水化温度场试验及数值模拟分析

周大为，邓年春*,2，石拓

(1.广西大学 土木建筑工程学院, 广西 南宁 530004;2.广西防灾减灾与工程安全重点实验室， 广西 南宁 530004)

0 引言

钢管混凝土拱桥因其优异的结构性能在我国得到迅速发展，随着建设需要，其跨径不断得到突破[1]。为了满足结构安全需要，拱肋截面钢管直径也势必相应增大，从而使得拱肋混凝土水化热问题显得更加突出。一方面，混凝土内部温度场在水化过程中受其影响，使得截面温度应力剧烈变化。混凝土水化凝结使得内部温度迅速上升，待水化放热速率低于对外散热速度时开始降温，此时混凝土遇冷变形，从而使得混凝土和钢管黏结面上的混凝土产生拉应力减小二者黏结力[2]，可能导致钢管混凝土脱黏和混凝土开裂问题；另一方面，管内混凝土灌注后的凝结硬化中，在内部自身热、外部气温及太阳辐射共同作用下，在空钢管合龙的基础上积累了一部分初应力，所以钢管混凝土拱桥的基准维度应以该应力进行反推求得。因此整个混凝土水化过程的温度变化对于合龙温度的研究至关重要。

林春姣等[3-4]对钢管混凝土结构，自灌注至成型过程进行了试验研究，并对不同截面形式的拱肋成型过程的水化温度分布，采用理论计算的方法进行了研究。研究表明：管内混凝土凝结硬化过程中放热引起的温度对拱肋应力影响较大，不同形式的拱肋对其温度分布亦有影响。孙国富等[5]研究认为：混凝土由于减水剂和膨胀剂的添加，使得其灌注完毕后存在较长的诱导期，在诱导期结束后迅速升温，且截面尺寸与截面水化温差呈现正相关。黄福云等[6]对百崎湖三跨钢管混凝土拱桥进行了实桥温度监测；林春姣等[7]以某哑铃型钢管混凝土拱桥为依托，对其拱肋成型过程进行了温度监测试验，研究了水化温度对结构施工过程的影响。为了描述混凝土水化凝结放热规律，朱伯芳[8]认为可采用指数式、双曲线式以及复合指数式等计算模型，对其进行理论分析。林春姣等[9-11]对水化放热模型进行了系列试验和计算研究，认为复合指数式模型相对更为精确。弹性模量及力学参数是计算截面温度应力及全桥温度效应的关键，混凝土在硬化过程中弹性模量的升高与混凝土水化放热几乎同步进行。朱伯芳[8]对大量混凝土弹性模量随材龄变化进行数据分析后认为，混凝土弹性模量采用复合指数式计算模型较好。但上述研究仅考虑了龄期的影响，目前有研究认为温度对混凝土强度及力学参数的影响不可忽略[12-14]。

虽然钢管混凝土水化热问题已经得到了一定的研究，但主要集中在中东部地区的钢管混凝土构件，对青藏高原地区大型钢管混凝土水化热试验研究目前还较少。本文对川藏铁路拉林线雅鲁藏布江大桥进行同尺寸试验拱混凝土灌注试验，管内布置温度传感器，在混凝土灌注完毕后对核心混凝土水化放热进行长期温度监控并结合有限元分析，探讨青藏高原地区大管径钢管混凝土水化放热规律。

1 工程概况

川藏线重点工程——藏木特大桥，采用一跨过江方案，为我国目前跨径最大的铁路钢管混凝土拱桥，其跨径达430 m。整座桥梁为连续梁结合钢管混凝土拱桥建造而成，两侧分别为71.6 m和62.6 m的连续梁桥，中部为钢管混凝土拱桥。桥梁的主梁为预应力混凝土连续梁结构，其沿桥梁纵向共分为5跨。钢管混凝土拱桥拱肋横截面为桁式截面，拱脚部分节段弦管为1.8 m管径的钢管混凝土结构，其他节段采用1.6 m管径的钢管混凝土结构。全桥拱肋结构中，弦管由Q420钢管灌注C60高强混凝土成型而成，其余拱肋结构均由Q345钢材制作而成。

2 试验概况

为确定钢管混凝土拱桥在外界自然条件下的内部温度分布情况及规律，为在青藏高原地区设计此类桥梁提供准确的温度效应计算参数，对川藏铁路拉林线雅鲁藏布江大桥进行足尺寸试验拱温度试验。试验选址于西藏山南地区雅鲁藏布江边，靠近川藏铁路拉林线雅鲁藏布江大桥桥址处。以实桥拱顶至拱脚75 m节段建立试验模型，试验现场见图1。试验拱由与雅鲁藏布江大桥相同管径1 600 mm，壁厚20 mm的钢管制作而成。试验拱由5组中间设置了横撑的立柱进行支撑。

以靠近拱顶位置作为试验测试截面，其中温度传感器由热敏电阻制成，与采集系统适配，采集精度达到0.1 ℃。采集仪器选用基康无线温度采集系统。采集频率设置为10 min/次。测点布置见图2。截面沿竖向和横向共布置13个温度传感器。

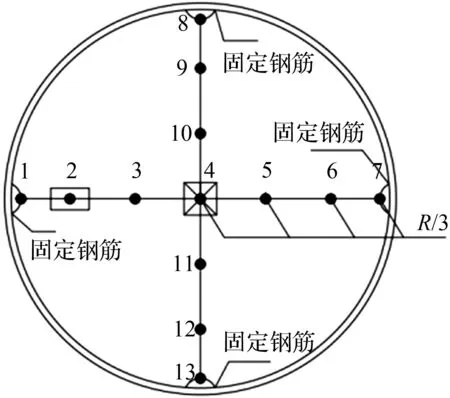
图2 测点布置图

2.1 管内混凝土灌注

试验拱管内混凝土灌注时间为2018年5月，其中5月份大气温度实测值如图3所示。混凝土灌注采用与实桥相同的三级泵送灌注方案，其中三级接力真空辅助灌注为核心技术，拱肋混凝土三级灌注布置如图4所示，具体流程如下：

① 泵送砂浆润滑管道，然后打开安装好的真空系统，将钢管内抽真空至负压-0.09 MPa。稳压10 min后，开通阀门，进行混凝土一级灌注。如图4(a)所示。

② 待一级灌注结束，关闭一级进浆管道出浆管道，转换进入混凝土二级灌注。打开二级进浆管道泵送混凝土。如图4(b)所示。

③ 待二级灌注结束，关闭二级进浆管道出浆管道，转换进入混凝土三级灌注。打开三级进浆管道泵送混凝土。最后，继续泵送，出浆管冒出浓浆，整个混凝土灌注过程结束，如图4(c)所示。

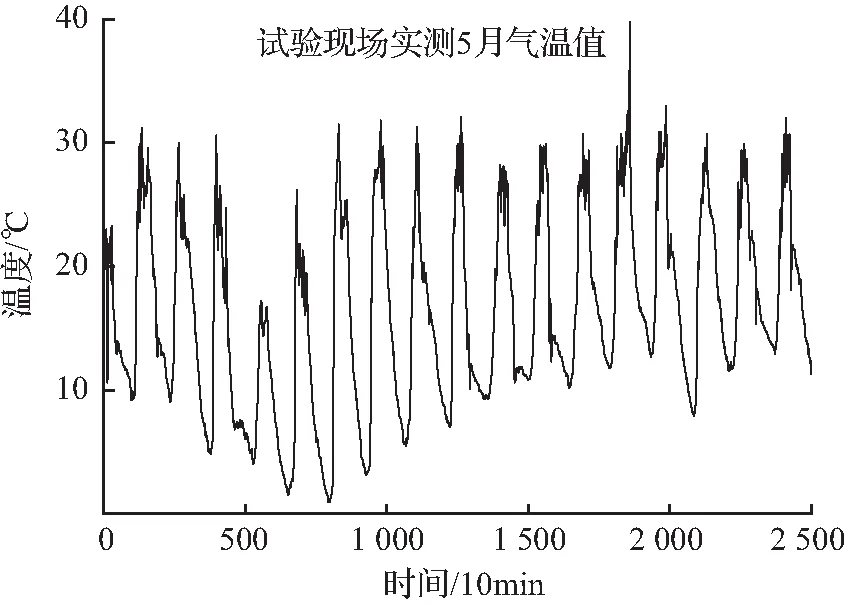
图3 气温时程变化

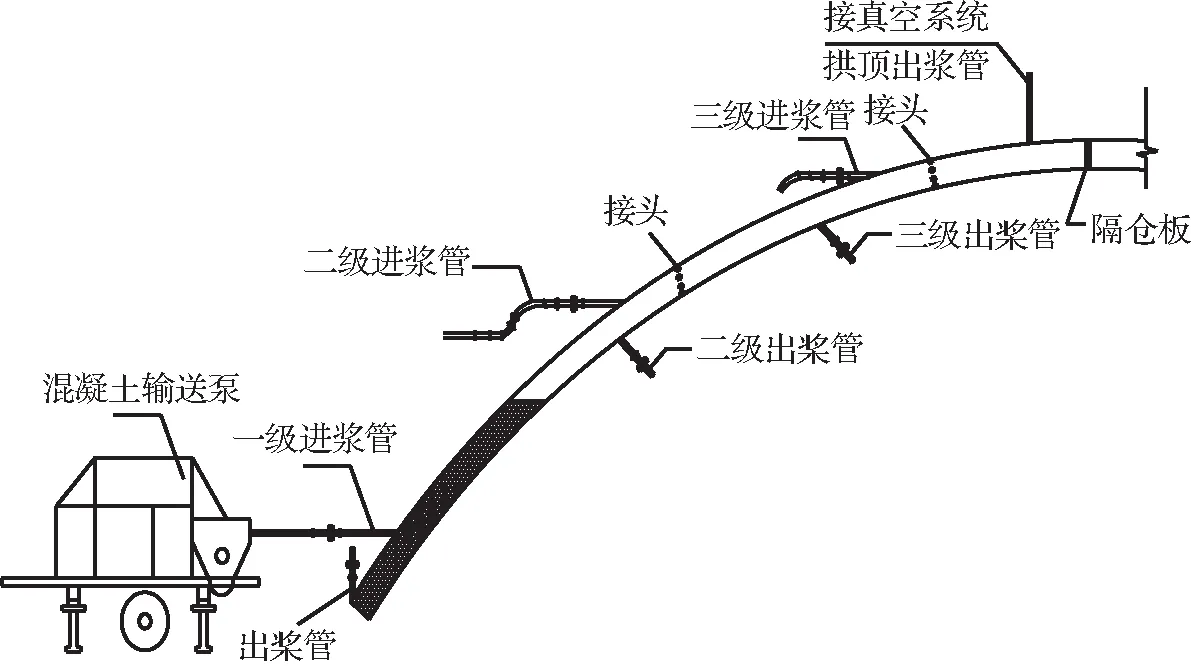
(a) 一级灌注

2.2 水化热数据分析

从灌注混凝土起对管内混凝土测点温度变化进行连续观测。为对比日照对钢管混凝土水化放热的影响，取有日照影响测点及阴影处测点的温度变化曲线进行分析，分别如图5、图6所示。各测点温度均呈现出先波动变化后迅速上升至温度峰值再缓慢下降直至趋于大气温度，到达稳定阶段后受大气温度变化的影响呈现周期性变化，其中外部测点温度受外部环境影响较大，变化幅度较大；内部测点受大气温度影响较小，变化幅度较小。

图5 阳面测点温度变化

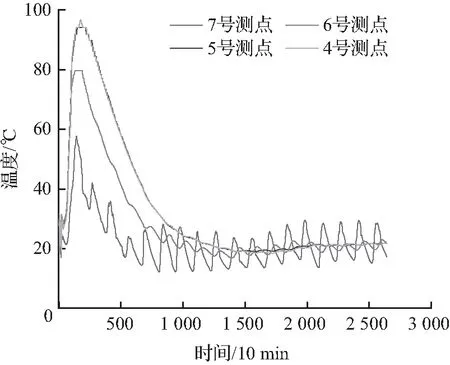
图6 阴面测点温度变化

混凝土初始入仓温度为28.3 ℃，混凝土灌注采用三级泵送灌注方案，混凝土在管内处于流动状态直至充满钢管内部，故而各测点初始温度有约3～5 ℃的温差。管内混凝土由于外加剂(减水剂、膨胀剂)的掺入，使得混凝土没有立刻发生水化反应，存在诱导期约4～5 h。管内缓凝土灌注完毕4～5 h后水化热剧烈释放，在灌注完毕22 h左右(即水化开始后约17 h)达到温度峰值。对比图5和图6发现，内侧测点温度相较于外侧测点温度受日照影响较小，且阳面与阴面内外测点温差极值相差约3～4 ℃，故认为日照对截面温差影响较小；外部测点达到温度峰值时刻较圆心基本一致，达到较稳定温度时刻早约3 d。

以背阴面为例，灌注完毕后22 h左右核心混凝土达到水化热温度峰值近100 ℃，温度峰值时刻，管内混凝土因水化而产生的温差达42 ℃。测点7由于靠近截面外侧受外部影响较大且钢管散热率较高，使得该测点温度上升较为缓慢；测点4升温速度最快且升温过程中曲线平滑，说明内部混凝土升温过程受外部环境温度周期变化影响较小；测点5、6、7在降温阶段受外部环境温度的谐波变化影响，温度呈现波动下降状态。上述各测点温度随时间变化情况表明：混凝土中掺入缓凝剂及减水剂后的水化情况较普通硅酸盐水泥水化过程差异较大，在进行有限元数值计算时应充分考虑该类混凝土的诱导期。

2.3 水化温度场有限元计算分析

2.3.1 水化放热模型

图7 计算模型

本次试验采用C60无收缩混凝土进行灌注。针对拱肋进行水化分析时可将三维空间温度问题转化为二维平面问题进行计算，参考[9]采用复合指数式水化计算模型进行计算分析，见公式(1)。基于有限元软件ANSYS热分析模块，采用热分析单元PLANE55号单元进行计算分析，划分网格后的模型见图7。整个截面划分为1 360个单元和4 155个节点。雅鲁藏布江特大桥拱肋钢管均采用Q420，管内灌注C60无收缩混凝土。材料热膨胀系数参考英国《钢混组合结构设计规范》[15]、美国《钢结构建筑荷载系数设计规范》[16]。

复合指数式模型

Q(t)=Q0(1-e-atb)，

(1)

其中：Q(t)为龄期为t时的总的水化热(kJ/kg)；Q0为总水化热量(kJ/kg)；a，b为参数。

2.3.2 有限元数值模拟

试验结果表明，日照对水化阶段截面内部温度影响较小，故本文在进行管内混凝土水化放热数值模拟分析时，在简化计算量并保证计算精度的基础上作以下假设：钢管和混凝土接触良好，二者之间的热流传递连续不间断；钢管混凝土拱肋纵横比非常大，故认为各截面所处环境基本相同不考虑沿纵向的热传导，故可用计算二维平面问题的方法，计算拱肋水化温度分布问题；不考虑日照的影响。取混凝土初始温度为28.3 ℃、钢管初始温度取20 ℃、环境温度取2018年5月平均最高和最低气温按正弦函数拟合的日气温变化进行计算，五月份当地平均风速约为3级风。计算中，水化初始时刻为混凝土诱导期结束时刻，即混凝土灌注完毕后5 h为水化初始时刻。各测点水化温度计算值随时间变化情况如图8所示，其中测点选择位置如图7所示,其中4个位置的测点分别对应试验中测点4～7。

图8 管内混凝土温度变化

对比可以看到，复合指数式水化计算模型在各个测点处的温度变化趋势较实测值均较为相符，核心处温度峰值相差约4 ℃，截面温差极值相差约5 ℃，其他测点峰值温度及峰值时刻较为相近。研究结果表明：日照对大管径钢管混凝土内部水化热影响较小，故在大直径钢管混凝土水化热有限元计算中可不考虑日照影响以简化计算。各测点温度计算值在考虑外部日气温的周期性变化的情况下可以很好地对应管内混凝土各测点温度的实测变化情况，外部测点受气温影响较大，在升降温过程中均呈谐波状态。实测值与计算值基本相符，验证了复合指数式水化计算模型在西藏地区的钢管混凝土拱桥混凝土水化放热温度计算上的适用性。核心混凝土水化热呈现出先上升再下降的内高外低的温度分布状态。

3 水化温度效应分析

在计算钢管混凝土结构由于水化温度场引起的温度应力时，必须考虑弹性模量与混凝土水化龄期的关系才能得到较为精确的水化温度效应值。当前对于混凝土弹性模量与材龄关系的描述主要有指数式、复合指数式、双曲线式以及对数式，复合指数式模型较其他模型而言具有较高的计算精度[8]。混凝土弹性模量在灌注7 d左右便可达到标准值的90 %以上。

在水化初期，混凝土释放大量的热量使得混凝土与钢管受热膨胀，由于此时刻混凝土强度与弹性模量较低，使得该时刻截面混凝土温度应力较小；后期，混凝土水化放热速率低于外部散热率时，截面温度开始下降，此时混凝土已达到一定强度，而钢管遇冷收缩，收缩过程中受混凝土约束产生较大的温度应力。图9为混凝土截面温度效应图。图9(a)表明此时混凝土径向受压应力。该时刻混凝土环向温度应力如图9(b)所示，由图9(b)可知：混凝土和钢管交界面最大环向应力达2.9 MPa，该值大于C60混凝土抗拉强度设计值2.04 MPa，约等于其抗拉强度标准值2.85 MPa，极有可能造成混凝土开裂及脱黏问题的发生。

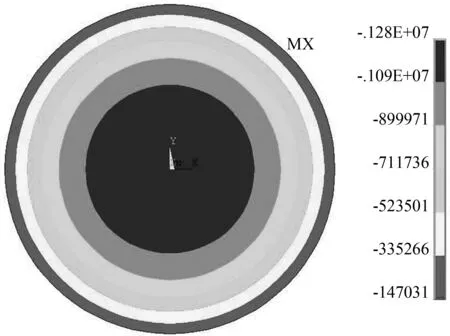
(a) 径向

4 水化热影响因素分析

为降低大直径钢管混凝土拱桥拱肋混凝土水化热引起的不利影响，本文着重研究混凝土入仓温度和灌注时外部环境温度对水化热的影响，寻求合适的灌注条件以降低水化放热对结构造成的不利影响。

采用实桥管径1.6 m，壁厚36 mm的单圆钢管为研究对象进行分析。入仓温度影响分析时，外部环境温度取试验拱灌注时刻平均温度20 ℃为定值，考虑入仓温度分别为5、15、25、35 ℃进行分析，核心混凝土水化温度变化见图10。环境温度影响分析时，混凝土入仓温度取20 ℃，分别采用10、20、30、40 ℃模拟川藏铁路拉林线雅鲁藏布江大桥拱肋混凝土各季节施工环境温度。模拟仿真结果见图11。

计算结果表明：入仓温度为35 ℃时的截面极值温差较入仓温度为5 ℃时的截面极值温差高约17.6 ℃。入仓温度每升高5 ℃，钢管混凝土截面温差极值增大约3 ℃。入仓温度为20 ℃时，环境温度每升高5 ℃，钢管混凝土截面最大温差约降低2.5 ℃。虽然较高的外界环境温度使得核心混凝土温度极值较高，但是较高的外部环境温度可使得钢管混凝土截面的最大温差较低。各入仓温度及环境温度影响下，钢管混凝土截面最大水化温度差值见表1。

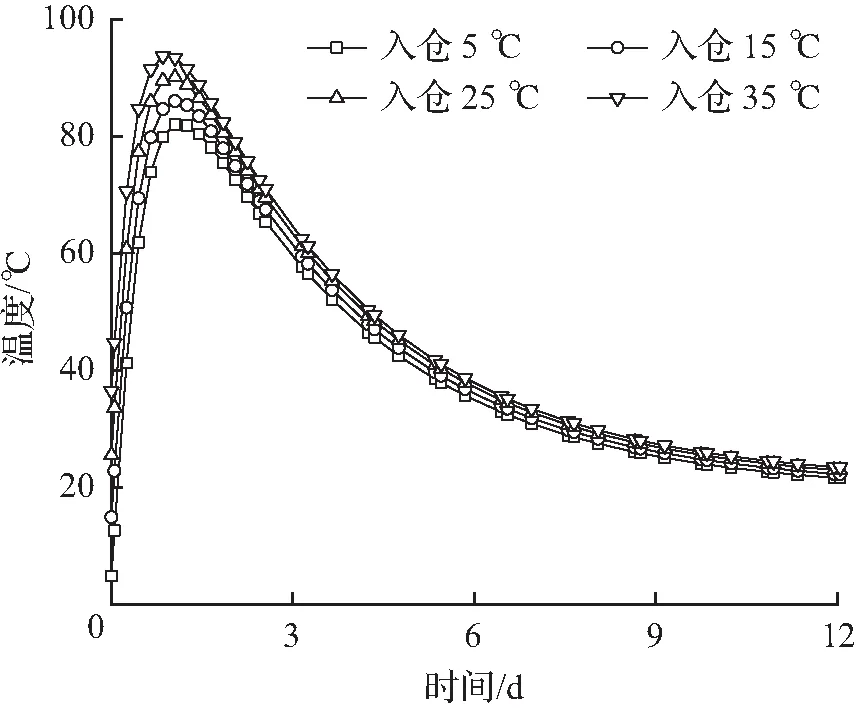
图10 不同入仓温度混凝土中心温度变化

图11 不同环境温度混凝土中心温度变化

表1 截面最大温差

综上可知，混凝土在灌注时可采取措施降低其入仓温度以达到降低水化热影响，如使用冷水甚至冰水进行拌制。灌注时刻温度不宜过低，冬季施工需要采取保温措施以降低截面温度梯度带来的不利影响，如采用棉被或聚氨酯泡沫保温层进行包裹等。

图12为分别在钢管外围包裹泡沫保温层和无保温层条件下的截面各测点温度变化情况。计算中假设混凝土和钢管紧密贴合，钢管和保温层紧密贴合，其入仓和环境温度为20 ℃。由仿真结果可知，考虑保温层情况下钢管混凝土截面最大温差约为26.3 ℃，发生时刻约为2.6 d；小于无保温层情况下的45 ℃温差。仿真结果表明，加设保温层虽然推迟了温度峰值的发生，但是可以显著降低截面温差，并以此来降低水化温度引起的不利影响。

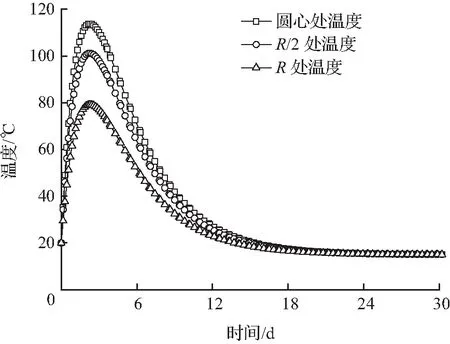
(a) 有保温层

5 结论

对川藏铁路拉林段藏木雅鲁藏布江特大桥拱肋混凝土灌注过程中水化热问题及影响因素进行试验及有限元计算研究，得到以下结论：

① 钢管混凝土拱肋混凝土水化呈现先上升再下降的内高外低的温度分布状态；水化初期，混凝土水化放热迅速使得管内混凝土温度较高，由于此时混凝土弹模较小和徐变影响，混凝土的应力较小。水化后期，混凝土水化放热量减小直至结束，此时混凝土形成强度，会在和钢管接触处产生较大的拉应力。

② 钢管混凝土结构与外界环境热交换计算的关键在于边界条件的准确施加。水化过程中太阳辐射对截面内部温度分布影响较小，故在对大管径钢管混凝土水化热计算时可不考虑太阳辐射边界条件以简化计算。

③ 混凝土中掺入缓凝剂及减水剂使得混凝土灌注后存在水化诱导期。对该类混凝土进行水化温度分布数值计算时需对混凝土水化诱导期予以重视，以得到符合实测的数值解。以诱导期结束为水化初始时刻，结合复合指数式计算模型可以较好地描述西藏地区大管径钢管混凝土水化放热规律。

④ 混凝土入仓温度和外界环境温度对管内混凝土水化影响很大，其中：入仓温度每升高5 ℃，钢管混凝土截面温差极值增大约3 ℃；环境温度每升高5 ℃，钢管混凝土截面最大温差约降低2.5 ℃。混凝土拌制可用凉水或冰水，以此来降低其入仓温度过高引起较大的截面温度梯度；在混凝土水化过程中采用保温层包裹钢管可有效降低钢管混凝土截面的温差，降低水化对结构产生的不利影响。