基于奥苏贝尔有意义学习理论的数学归纳法教学
曹露乙
(广东省佛山科学技术学院 广东 佛山 528011)
1.引言
不管新高考如何改革,数学归纳法这一章节知识依然是教学重点。因为它不仅有助于数列、不等式等题型的解决,更能培养学生思维的严谨性。但目前对于数学归纳法教学,几乎是“三段式”程序的机械传授,学生也是生搬硬套的机械学习,或许题目可以做,但学生并不懂为何要这样证明,更不懂它的中心思想是什么,实质是什么,最终也就没实现有意义学习。
2.有意义学习理论
奥苏贝尔提出的有意义学习是针对机械学习而言的,是指在学习知识过程中,将以符号表示的新知识与学习者认知结构中已经存在的相应概念进行实质性的和非人为的联系。所谓实质性联系是指符号为代表的新知概念与学习者现有认知结构中的表象、概念、命题建立内在联系;非人为联系指符号所代表的新知与认知结构中的表象建立逻辑连接。[1]奥苏泊尔强调新旧知识的联系与同化。
3.数学归纳法理论结构
数学归纳法是特殊的归纳法,因为其本质采用的是演绎证明。一般来说,所有与自然数有关的命题都可以用数学归纳法来证明。[2]如果要证明一个与正整数n有关的命题,记为P(n),则数学归纳法可按以下步骤:
(1)证明当n取第一个值n0时命题成立;
(2)假设n=k(k≥0)时命题成立,能够推导出n=k+1时命题也成立;
(3)综上两个步骤,就可断定命题对从n0开始的所有正整数n都成立。
综上可见,这是一个由“个别—特殊—一般”的推理形式,符合归纳推理的程序。但数学归纳法它的逻辑更严谨,最后一步还需要演绎推理加以证明,只能说归纳法作为数学归纳法的必要前提,归纳为应用数学归纳法去证明相应的结论打下了基础,其本身还是严格的演绎推理过程。
4.当前数学归纳法教学中存在的问题
4.1 分不清归纳、归纳法、数学归纳法。许多老师在讲数学归纳法时,都没有提归纳、归纳法、数学归纳法三者间的关联,以至于学生觉得是同一个概念。归纳是基于逻辑思维得出结论的过程。归纳法是人们在日常生活中使用的一种推理证明方法,其结构是似真的。数学归纳法是一种演绎方法,它的结论是真的。三者依次递进,依托向上,走向更严谨、更科学的方向。
4.2 难以理解用有限步推理来代替无限步推理的思想。数学归纳法不是不完全归纳法,不能通过前几项就归纳出结论。也不是完全归纳法,它不能把无穷多个数都列尽。但它却使用了有限次的验证(P(n0))和一次逻辑推理(P(k)成立→P(k+1)成立),代替无限次的验证,通过演绎的证明,推导出结果的正确性,从而实现了从无限到有限的转化,这也是数学归纳法的实质。
4.3 学生不理解“假设结论成立,然后再去证明结论成立”。“p(k+1)的证明过程建立在p(k)上,p(k)未被预先证明,并且在推理过程中也同样不加证明,为何如此假设?”以上的困惑来源于教师在讲授时没分析“包含关系”。数学归纳法的目的不是证明p(k)和p(k+1)分别成立,而是它们之间是否存在包含关系,该包含的关系能够推演出命题为真值,这与p(k)和p(k+1)是否成立没有关系[3]。
4.4 递推关系证明的数学困难。学生在学习“三段式”后,明白只要生搬硬套使p(k+1)成立,题目就迎刃而解了,从而造成许多的假证明,没有理解真正的内在关系,最终造成机械学习。
5.有意义学习在数学归纳法中的应用
针对以上数学归纳法教学现存缺陷,笔者试图通过以下教学案例,使学生在进行数学归纳法学习中实现有意义学习。
5.1 创设情境,引入新知。
情景一:之前学习过归纳推理时,遇到这样一个问题:

问题一:大家是如何求的呢?

问题二:当时猜想正确吗?n取无穷可以证明吗?
这里的提问与学生认知发生冲突,学生会意识到正整数无穷,无法一一检验。
问题三:怎样才能进行无限的验证呢?亟待找到新的方法。
5.2 问题链驱动,激发思辨。
问题四:在之前学习中,有遇到过类似的问题吗?
情景二:以“求f(x)=x2单调区间”为例。
①方法一:画图法。取值带入,描点作图,找出图像上的单调增区间和单调减区间。对于无穷远的实数,依然不知是否成立。
②方法二:求导法。对函数进行求导,当x>0时,f(x)′>0,是增区间,当x<0时,f(x)′<0,是减区间。
问题五:由这个例子,可以得到什么启发?
虽然这里以教师讲授为主,但却是有意义的接受学习。通过引例,激发学生思考:能否通过验证有限步骤的有效性来确保无限步骤的有效性?
5.3 知识迁移,形成概念。为解决“有限步确保无限步的成立”这个问题,接下来利用多媒体演示多米诺骨牌游戏视频。
情境三:多米诺骨牌实验
实验一:老师推倒第1块多米诺骨牌,然后第2块,第3块,第...块都倒下,实验成功。

问题六:在什么样的条件下,出现了这样的结果?
此时学生心里一定会有答案,即第一块骨牌倒下,前一个给后一个推倒。根据最近发展区理论,让学生自己总结概念,继续类比实验。
实验二:教师没有推倒第1块骨牌,接着第2块,第3块,第...块都没有倒下,实验失败。

问题七:对比试验一与二,分析实验二失败原因?
此时学生就会意识到,若想试验成功,第一要义就是让第一块骨牌倒下。
实验三:将第4块骨牌和第5块骨牌拉大间距,使间距大于骨牌横截面的长,教师推倒第1块骨牌,接着第2块,第3块,第4块全部倒下,但第5块并没有倒下,随后的也没有倒下,实验失败。

问题八:对比试验一与三,分析实验三失败原因?
根据以上分析,学生明白:实验成功的第二要义就是相邻的两块骨牌前一块倒下一定导致后一块倒下。
针对上述实验,让学生总结多米诺骨牌全部倒下的条件:
⑴第一块要倒下;
⑵当前面一块倒下时,后面一块必须倒下;
当满足这两个条件后,多米诺骨牌全部都倒下。
根据多米诺骨牌的实验使学生大概了解了数学归纳法的雏形,也认识到两个步骤的必要性。但生活情境毕竟不能体现出数学的严谨性,还需要迁移到数学问题,对已有的知识进行同化。
回顾:回到情境一,解决数学问题
问题九:受多米诺骨牌的启发,能否使情境一得到严谨的证明呢?
证明:①我们已经验证了第一个等式成立。
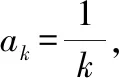
5.4 反馈练习,巩固提高。
及时的反馈不仅是对老师教学的鞭策,更能使学生及时了解自己,提高自我效能感,从而提高学生学习动机的认知动力。
6.有意义学习对数学归纳法的启示
6.1 完善学生头脑中已有的认知结构,将知识同化升华。数学归纳法在此之前已经或多或少的渗透过,根据高中生身心发展和记忆的特点,就能够在头脑里建立有关数学知识的认知结构,这就为有意义学习做了铺垫。所以在教学开始前,设计对数列的讲解,表明了不完全归纳法的缺陷,既注重了学生的“最近发展区”教学,又使学生产生认知冲突,随后通过多米诺骨牌的游戏,使学生“跳一跳就摘到果子”,总结出概念。根据奥苏贝尔认知同化理论,学生通过有意义学习,可以将原有的认知结构进行升华,形成新的认知结构。
6.2 数学课堂设计的要有层次性,沟通新旧知识的联系。奥苏贝尔提出的先行组织者策略旨在教师通过简单易懂的讲解,使学生利用旧知去同化新知。因此教师在设计导入环节时,可以从学生实际情况出发,尽可能提供起点低、易于学生理解的引导性材料。本文设计的数列作为先行组织者,使学生产生矛盾,接着使用二次函数和多米诺骨牌,引出数学归纳法的重难点,学生在有层次的课堂设计下,进行了有意义学习。
6.3 正确反馈学生学习成效,激发学习动机。奥苏贝尔的有意义学习理论同样强调了学生的学习动机。因此教师在数学归纳法概念教学完成后,典型练习,巩固训练必不可少。只有及时反馈学生的学习情况,了解自己的学习效果,才能激发学生进一步学习的主观愿望,提高学生的学习动机。[4]

