数学思想方法在初中数学解题中的应用
熊海龙
【摘 要】数学思想方法属于数学教学中的重点内容,同时也是学生掌握知识、保持思维活跃性的重要工具之一,借助数学思想方法能够更好地解决数学问题。在初中数学教学中,教师需要做好问题设计,锻炼学生运用数学思想方法的能力,加深学生对数学知识的理解,提升学生的解题能力。
【关键词】数学思想方法;初中数学;解题
在初中数学教学中,数学思想方法能帮助学生解决数学问题。在教学中,教师需要从转变传统教学观念开始,充分挖掘教材知识,做好教材知识的讲授,及时引入数学思想方法,帮助学生找出解决数学问题的方法。转变教学模式,不仅可以促进教学中数学思想方法的有效渗透,同时可以逐渐提升学生的数学解题能力。
1 初中数学教学中引入数学思想方法的意义
初中数学学习中,学生只有掌握数学思想方法,才能加深对数学知识的理解,才能构建出完整的知识体系,主动将学到的数学知识运用到解题过程中。在传统数学教学中,教师因长期受到传统教育理念的影响,习惯使用“灌输式”“题海式”等教学模式,使学生只能被动接受教师所讲述的内容。学生长期在这种模式下学习,会逐渐对数学学习产生抵触心理,其学习的主动性、积极性会不断降低。在初中数学教学中引入数学思想方法,不僅可以帮助学生掌握数学学习技巧,让学生在解题中使用合适的数学思想方法,逐渐提升数学思维能力,提高数学知识运用的灵活性,也可以帮助教师将抽象的知识点以直观的方式展示出来,在一定程度上降低数学知识的复杂性,提升数学教学质量[1]。
2 数学思想方法在初中数学教学中应用的原则
2.1 启发性原则
在应用数学思想方法时,教师应坚持从启发性原则出发,做好思想启发与指导工作,发挥自身的引导作用。由于数学思想有一定的抽象性,难以进行详细的传输,所以教师需要结合教学活动,以培养学生的感悟、理解与思考能力为主,确保学生深入理解数学思想和掌握数学知识点,实现数学教学目标。在使用数学思想方法时,还要挖掘教材中的内容,以完善教学大纲与计划为主,将学生带入学习活动中,锻炼学生解决数学问题的能力[2]。
2.2 因材施教原则
在培养学生解决数学问题的能力时,应当结合数学问题,做好数学思想方法的引入工作,掌握学生的具体情况,坚持因材施教原则。由于学生在个性特点与学习能力等方面存在着明显的差异性,所以在教学中,教师需要掌握每个学生的具体情况,采取适合的教学方法,让学生在适合自己的层次得到锻炼,不断提升学习能力。
2.3 循序渐进原则
合适的数学问题能够让学生产生探究欲望,同时也可以让学生在思考与学习中主动运用数学思想方法,在不断探索中掌握解题技巧,进而提升数学教学质量。因此在教学中,教师要从发展的角度出发,利用合适的训练方法,确保教育活动的高效开展。教师也需要做好总结与分析工作,与学生一起针对数学问题进行探究,帮助学生构建完善的数学知识体系,使学生主动将掌握的数学知识运用到解题中。
3 数学思想方法在初中数学教学中应用的措施
3.1 挖掘教材内容
初中数学教师要从合理引入数学思想方法入手,保证教学的灵活性,利用适合的问题启发学生,将抽象的知识以直观的方式展示出来。对此,教师需要先做好将教学素材的挖掘工作,找出合适的教学素材。教师要对数学教材进行深入分析,坚持合理性原则,在熟练使用教材的基础上转变传统教学模式,鼓励学生将所学数学知识与生活联系起来,理解与使用数学知识。在课堂教学中,教师要从全面概括与研究出发,运用适合的方法,加深学生对数学知识的理解。如运用方程思想方法需要针对数学问题进行分析,从设立方程入手,找出解题措施。方程思想方法属于比较常用的思想方法,对帮助学生掌握数学知识有重要的促进作用,不仅可以帮助学生理顺学习思路,还可以帮助学生形成数学思维。数学教材中涉及较多数学方程思想,如利用根、系数之间的关系求出字母系数的值等。教师也要及时更新自身教学思想,将学生带入数学学习中,明确探究方向。如在讲解“利用待定系数法确定二次函数解析式”时,需要从引导的角度出发,鼓励学生以自主探究的方式找出不同系数,确定最后的解析式等。适合的教学活动能够锻炼学生运用数学思想方法解决问题的能力,同时可以帮助学生加深对数学知识之间联系的理解[3]。
3.2 数形结合法的应用
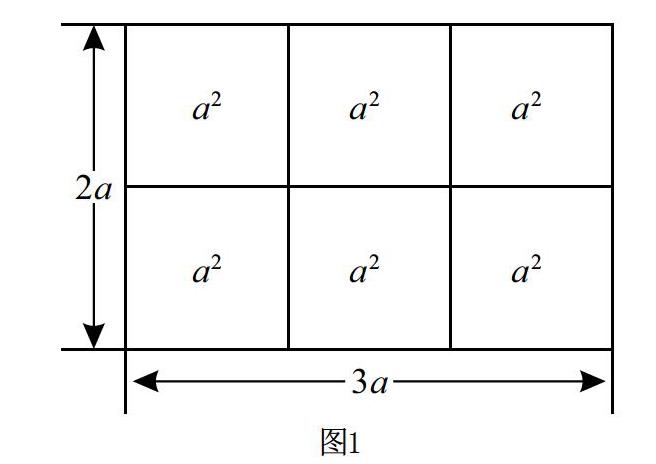
在初中数学教学中,运用数形结合思想方法能够刺激学生的视觉,让学生对数学知识产生探究欲望,在主动思考与学习中,保持学习动力。学生参与数形结合活动,不仅可以提升自身的形象思维能力,同时也可以在解题中逐渐完善自身的数学知识体系,然后主动将掌握的数学知识运用到解题中。如在讲述“单项式与多项式的运算法则”这一内容时,因这一内容属于初中数学教学中的重点,也是学生学习的难点,所以教师需要发挥数形结合的优势,以形象、生动的教学方式吸引学生,减轻学生的学习压力,让学生真正掌握数学知识,逐渐形成清晰完整的数学知识体系。如在讲解“求 2a·3a 的值”这一内容时,教师可以画出图形(见图1),引导学生将 2a 看作长方形的宽,将 3a 可以看作长方形中的长,所以 2a·3a 也就可以看作长方形的面积。
3.3 化归数学思想的应用
初中数学教材涉及比较丰富的定理、公式以及概念等。研究发现,许多学生在学习、解题等环节不仅出现了思维混乱问题,甚至还出现了错误使用数学定理、公式等问题。针对这一现象,在开展数学教学活动时,应当从运用划归数学思想方法入手,确保学生对数学知识产生清楚的认识,并在理清数学解题思路的基础上掌握重点知识,构建出完善的数学知识体系。如在讲解“求解数代数方程”时,就可以从使用化归思想入手,将复杂的知识点以具体简单的方式表达出来,最终转变成为一元二次方程或是一元一次方程等。化归数学思想方法也被称为高次方程低次化,在初中数学解题过程中使用化归数学思想方法,不仅可以锻炼学生应用转换与联想思想方法的能力,同时可以启发学生的数学思维,让学生在学会转化方法的基础上解决数学问题。如一动圆经过定点 F1(c,0),且和定圆(x+c)2+y2=4a2(a>0,c>0)是相切关系,那么求出动圆 O 的轨迹。在面对这类型题时,学生需要判断 a 和 c 的大小关系,然后将其划分成为三种情况进行探讨。最后就可以针对相切条件进行分析,找出对应两圆半径与圆心距离的关系,设立解析式。使用这一方法可以将等解析式化归成圆锥曲线,同时计算出结果[4]。
3.4 营造教学情境
新课改背景下,就要从转变传统教学模式出发,让学生对所要学习的数学内容产生学习兴趣,化解学生对数学知识的抵触心理,从而使学生主动参与数学学习活动中。营造适宜的课堂氛围,让学生感受到学习数学知识的乐趣,同时在适宜的情境中理解数学思想方法,并主动将所掌握的数学知识运用到生活中,实现学以致用的目标。教师需要及时引入先进教学理念,做好数学思想方法的引入工作,鼓励学生运用数学知识解决问题,从而使学生感受学习数学知识的意义,在学以致用中加深对数学知识的理解。如在讲述二次函数知识时,可以从营造与实际生活相符的情境出发,让学生在探索与学习中掌握数学问题,加深对数学知识的理解。如题:在商场中原价为20元的产品,以25元的价格销售,一个月一共能够卖出300件,当销售价格每次涨价1元钱时,每个月的销售量就会减少50件,请计算价格为28元时,销售量与月利润是多少。”在展示完题目后,教师可以要求学生进行小组探究,在找出其中数量关系的基础上计算问题答案。
综上所述,初中数学解题教学中,要从合理使用数学思想方法入手,针对数学内容进行分析,以引导、启发、创新等方式来吸引学生,让学生在主动探究与学习中找出解决问题的方法,提升自身应用数学思想方法解决数学问题的能力,实现数学教学目标。
【参考文献】
[1]李利娟.例谈数学思想方法在初中数学解题中的应用[J].留学生,2016(2).
[2]廖祥琴.试论数学思想方法在初中数学解题中的应用[J].文渊(中学版),2019(7).
[3]马伟华.数学思想方法在初中数学教学中的运用[J].课程教材教学研究:中教研究,2017(5).
[4]袁一鸣.浅谈初中数学思想方法在解题中的应用[J].新课程
(教育学术版),2009(12).

