互感中副线圈电流的反馈作用与自感的基础性作用
林辉庆


摘 要:教师和学生对互感系统中电磁感应现象的认识普遍存在着两个误区:忽视副线圈电流对原线圈的感应作用;忽视线圈的自感作用。文章通过推导一般互感系统原、副线圈的电流、电压间的相互关系和理想变压器原理,揭示了副线圈电流在原线圈中感应的反馈作用和自感的基础性作用。
关键词:互感;自感;正弦式电流;反馈;电能传输
中图分类号:G633.7 文献标识码:A 文章编号:1003-6148(2021)3-0056-3
互感是普遍存在的电磁感应现象,高中物理教科书对互感的定义是:当一个线圈中的电流变化时,它所产生的变化磁场会在另一个线圈中产生感应电动势,这种现象叫互感[1]。变压器的工作原理是互感,教科书指出:原线圈中的变化电流在铁芯中产生变化的磁通量,变化的磁通量在副线圈中产生感应电动势,所以副线圈能够输出电流[1]。在这里,既没有涉及副线圈电流对原线圈的感应作用,也没有涉及线圈的自感作用。教科书编写的不足,导致教师和学生对互感系统的电磁感应现象普遍存在着认识误区,以致对有关问题往往作出错误的推理与判断。
1 对互感系统电磁感应现象认识的两个误区
1.1 忽视副线圈电流对原线圈的感应作用
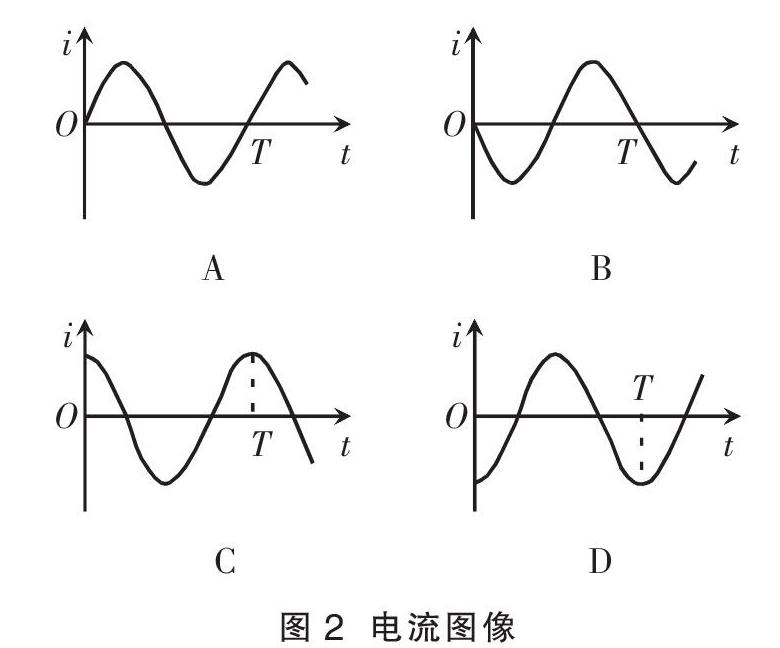
题1 手机的电磁感应式无线充电及原理如图1。原线圈(充电板中的线圈)接通交流电源后,它产生的交变磁场在副线圈(手机中的线圈)中激发感应电流,从而对手机实现无线充电。若原线圈电流i1随时间变化的图像如图2中的A所示,那么副线圈电流i2随时间变化的图像是哪一个?电流i1、i2的正方向规定如图1乙所示(i1、i2均为正方向时,它们在线圈中产生的磁场方向一致。下同)。
在中学教学中,大多按如下的推理来判断i2-t图像:t=0时■最大,i1产生的通过副线圈的磁通量变化率也最大,由法拉第电磁感应定律知道此时副线圈中感应电动势最大,由它产生的i2也最大;t=0后的一小段时间i1增大,由楞次定律判断出i2为负方向。由此得到i2-t图像为图2中的D,i2的相位比i1落后■。
上述推断,只考虑了原线圈电流i1的变化在副线圈中产生感应电流i2,根本没有考虑i2对原线圈的感应作用。i2在原线圈中的感应是客观存在的,那么,这种感应对i1的大小和相位有什么影响?这种影响在什么情况下才可忽略?是我们需要进一步搞清楚的问题。
1.2 忽视线圈的自感作用
题2 如图3,两平行金属导轨与理想变压器的原线圈连接,变压器副线圈连接电阻R。匀强磁场垂直于导轨平面,金属棒ab与导轨垂直且接触良好,ab棒与导轨的电阻均不计。ab棒在外力作用下沿导轨运动,下列情况中有电流通过电阻R的是( )
A.ab棒做简谐运动向右通过平衡位置时
B.ab棒做简谐运动通过右侧最远位置时
C.ab棒向右匀速运动
D.ab棒向右匀加速运动
常见的解析如下:ab棒做简谐运动向右通过平衡位置时,速度和切割磁感线产生的感应电动势最大,从而通过原线圈的电流和它在铁芯中产生的磁通量也最大;此时磁通量变化率等于零,副线圈中的感应电动势和通过电阻R的电流也都等于零。同理可推出,ab棒做简谐运动通过右侧最远位置时,通过电阻R的电流最大;ab棒做匀速运动时,通过电阻R的电流等于零;ab棒做匀加速度运动时,通过电阻R的电流为不等于零的某个定值。答案为B、D选项。
上述分析中,除了没有考虑副线圈电流对原线圈的感应作用外,还存在一个问题。那就是认为ab棒的电动势最大,流过原线圈的电流也最大;ab棒的电动势不变或变化,流过原线圈的电流也不变或同步变化。这是不自觉地将原线圈当作电阻器,用欧姆定律作出的推断。但由于原线圈回路的电阻等于零,只要ab棒的电动势不等于零,由欧姆定律就会得出电流趋于∞的结论。其实在这里,對电流起作用的是线圈的自感,那么,线圈的自感在互感中起什么样的作用?是如何起作用的?就成了我们需要进一步探讨的问题。
2 一般互感系统原、副线圈的电流、电压间的相互关系
2.1 互感系统中电流、电压关系方程
设图1乙中原、副线圈的电阻不计,匝数分别为N1、N2。原线圈接通交变电源后,通过原、副线圈的交变电流分别为i1、i2,交变磁通量分别为Φ1、Φ2,交变的磁通量在原、副线圈中产生的感应电动势分别为eab、edc。原、副线圈两端的电压u1(=uab)、u2(=ucd)与电动势的关系是u1=-eab、u2=edc,由法拉第电磁感应定律可得
u1=N1■,u2=-N2■(1)
需要特别指出,Φ1、Φ2是通过原、副线圈的总磁通量,它等于自身的电流产生的磁通量与另一个线圈的电流产生的磁通量之和。因此,任一线圈上的感应电动势等于自感电动势与互感电动势之和。设原、副线圈的自感分别为L1、L2,它们之间的互感为M,u1、u2就可以表示为
u1=L1■+M■
u2=-L2■-M■
这就是原、副线圈中的电压和电流满足的方程。这两个方程右边的第一项分别反映i1、i2的自感作用,第二项分别反映i2对原线圈的互感作用和i1对副线圈的互感作用。
2.2 原、副线圈的电流、电压间的相互关系
在原线圈加电压u1=U1mcosωt,负载是电阻R的情况下,i1、i2是正弦电流。解这两个方程得
tanφ2=-■(2)
I2m=-■(3)
tanφ1=-■(4)
I■=■(5)
(2)到(5)式就是电流i1、i2和电压u2(=i2R)的大小和相位。各式中都有L1、L2和M,表明互感系统中的自感和互感都是不可忽略的。
3 理想变压器原、副线圈的电压、电流关系
在上述公式中,L1、L2以复杂的方式缠绕在一起,为了进一步从物理本质上搞清互感现象中互感和自感是如何起作用的,我们有必要研究互感作用最显著的理想变压器的工作原理。
3.1 理想变压器的条件
第一,没有漏磁,通过原、副线圈每匝的磁通量Φ相同。无漏磁时,互感、自感和线圈匝数之间满足[2]M2=L1L2,N1M=N2L1。
第二,原、副线圈的自感趋于∞。这是由于铁芯的磁导率μ很大,线圈中很小的电流就能在铁芯中产生很大的磁通量。
第三,没有损耗。既忽略原、副线圈的电阻,也忽略铁芯中的涡流和磁滞现象。
3.2 电压比与电流比
由于没有漏磁,通过原、副线圈的磁通量Φ1=Φ2=Φ,由(1)式得到
■=-■(6)
这就是理想变压器的电压比公式,“-”表示u2与u1的相位差始终为π。
由于L1→∞,不接负载i2=0时,i10→0。
接通负载i2≠0时,原线圈出现电流
i'=-■i2=-■i2,i1=i10+i'1
于是有
■=-■(7)
将(6)(7)两式的两边相乘得到i1u1=i2u2
它的意义是,原线圈的输入功率始终等于副线圈的输出功率。
4 副线圈电流在原线圈中感应的反馈作用
在理想变压器的原理中,我们清楚地看到i2对原线圈的感应所起的反馈作用:i2的感应使原线圈电流从i10=0变化到i1=i1′;电源据此向原线圈输入副线圈需要的功率u1i1(=u2i2)。改变负载使i2变化,i1=i1′和原线圈的输入功率也随之变化。
在一般的互感系统中,副线圈电流对原线圈的感应同样起着反馈作用:原线圈根据i2提供的“反馈信息”i1′,调节自身电流的大小与相位,电源根据这种调节为原线圈输入副线圈需要的电功率。改变负载使i2变化,根据“反馈信息”i1′,i1和原线圈的输入功率作同步变化。
由i1′=-■i2知道,只有在i2→0时,i2对原线圈的感应作用才可忽略。题1中的手机无线充电问题,i2一定较大,它对原线圈的感应作用不能忽略,因此D选项是错误的。在i2不能忽略的情况下,i2与i1的相位差Δφ的范围是■<Δφ<π,i2-t图像应如图5所示。
5 自感在互感中的基础性作用
从互感的起源上,我们能直接理解互感与自感的本质联系。产生互感的磁通量是产生自感的磁通量的一部分或全部(没有漏磁时),在两线圈相对位置一定的情况下,自感越大互感也越大,从原线圈向副线圈传输电能的效果就越好,反之亦然。因此,自感是互感的基础,在任何互感現象中自感都是不能忽略的。
考虑到变压器线圈的自感作用不能忽略,再来分析题2。做简谐运动的ab棒是一个交流电源,它通过平衡位置和端点时,电压u1分别为最大和零。由(6)式知道,在这两个时刻电压u2也是最大和零;由欧姆定律,电流i2也为最大和零。这与常见解析得出的结论正好相反。
ab棒做匀速运动时,加在原线圈两端的电压U1=Blv为定值,因此必有空载电流i10=k1t(k1是一个微小的常量),铁芯中的磁通量Φ=k2t,它们满足L1■=N1■=U1,副线圈两端的电压U2=N2■=■U1。通过电阻R的电流i2=■=■·■≠0,i2在原线圈中产生的i'1=■i2=(■)2■,原线圈的电流i1=i10+i1′≈(■)2■。可见,常见的解析中认为ab棒匀速运动时没有电流通过R这个判断是错误的。
同理推出,当ab棒匀加速运动时,通过电阻R的电流i2随时间均匀增大。
综合上述分析,题2的答案应该是A、C、D。
参考文献:
[1]彭前程,黄恕伯.普通高中教科书物理选择性必修第二册[M].北京:人民教育出版社,2019:38,56.
[2]赵凯华,陈熙谋.新概念物理教程电磁学[M].北京:高等教育出版社,2006:211-212+365.
(栏目编辑 罗琬华)

